防碰分离系数算法优选与邻井相对位置测量误差计算

刁斌斌， 高德利(中国科学院院士)， 胡德高， 江 创

(1中国石油大学石油工程教育部重点实验室·北京 2中石化重庆涪陵页岩气勘探开发有限公司)

随着丛式井及“井工厂”作业模式的广泛应用,井口间距减小、井网加密，井眼碰撞风险增加。评估井眼碰撞风险的方法主要包括：邻井距离扫描计算[1-4]、井眼位置不确定性分析[5-9]和分离系数计算[10-17]。分离系数计算模型中考虑了邻井距离和井眼位置不确定性的影响，因此根据分离系数计算结果指导井眼防碰施工作业是目前钻井现场普遍采用的方法。目前已提出的分离系数计算方法尚不完善，具有各自的优缺点。

为了实现分离系数计算方法的优选，笔者在分析分离系数计算原理及其局限性的基础上，建立了邻井相对位置测量误差计算模型，提出了基于邻井相对位置测量误差计算与三维可视化结果优选分离系数算法的方法。

一、分离系数的计算方法

分离系数的计算方法主要包括：传统方法、垂足曲法[10-11]、中心向量法[12-15]、最小间距法[16]和缩放法[12,17]。其中，前四种方法计算分离系数f可以统一表示为：

(1)

式中:RS—邻井距离扫描计算得到的扫描半径，在邻井防碰设计和施工中主要用最近距离扫描半径；E—参考点和扫描点的测量总误差；r—参考井与比较井井眼半径的和。

只是在计算分离系数过程中，前四种方法对参考点和扫描点的测量总误差E的计算方法不同。计算分离系数的缩放法是通过同比例缩放参考点和扫描点的误差椭圆/误差椭球使之满足外切条件，与之对应的缩放系数即为分离系数。

依据参考井和比较井相对位置测量误差计算方法不同，分为计算参考点和扫描点误差椭球的分离系数计算方法，以及通过计算参考点和扫描点合成误差椭球的分离系数计算方法。合成椭球的获得是通过计算参考点和扫描点测量误差协方差矩阵的和来计算求得的，因此通过分别计算参考点和扫描点误差椭球求得的参考点和扫描点测量总误差通常都大于通过计算合成误差椭球的方法求得的结果。

目前，一般认为通过计算合成误差椭球来确定参考点和扫描点测量总误差的方法更为科学，因此垂足分离系数(PSF)和定向分离系数(OSF)是目前最为常用的分离系数计算方法。其中，PSF是SPE Wellbore Positioning Technical Section(WPTS)推荐的方法，也是Landmark软件中采用的方法。

二、常用分离系数计算方法的局限性

1. 不同的分离系数计算方法适用于不同邻井相对位置关系

如图1所示，当A井作为比较井时，OSF的计算结果低估了参考井与比较井的碰撞风险，PSF的计算结果更为科学。然而，如图1所示当B井作为比较井时，PSF的计算结果高估了参考井与比较井的碰撞风险，OSF的计算结果更为科学。

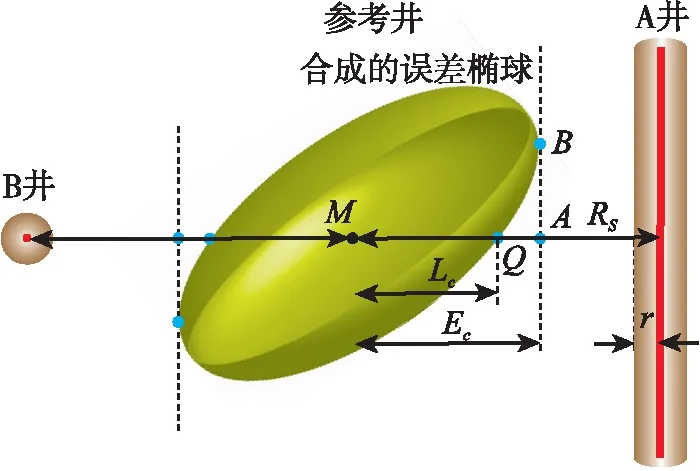
图1 不同邻井相对位置关系示意图

2. 未考虑井眼轨迹的几何形状

如图2所示，当A井作为比较井时，PSF等于1，但是比较井并未与合成误差椭球相交，即当比较井的轨迹形状向合成误差椭球方向凸时，PSF的计算结果高估了参考井与比较井的碰撞风险。然而，如图2所示当B井作为比较井时，PSF大于1，但是比较井已经与合成误差椭球相交，即当比较井的轨迹形状向合成误差椭球方向凹时，PSF的计算结果低估了参考井与比较井的碰撞风险。

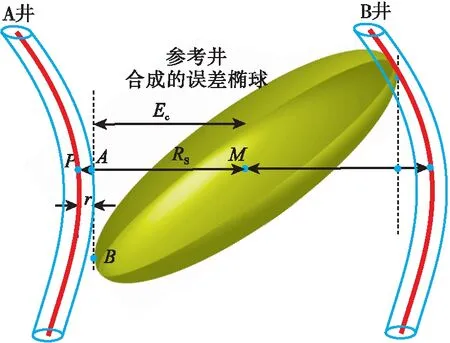
图2 不同井眼轨迹形状示意图

3. 未考虑井眼轨迹测量误差椭球形成的误差椭圆包络面

目前，分离系数的常用计算方法都未考虑误差椭圆包络面的影响，仅是简单地考虑参考点和扫描点的测量误差，必然导致分离系数的计算结果低估或高估参考井与比较的碰撞风险。

4. 邻井相对位置测量误差计算方法尚未完善

分离系数计算的基础是邻井距离扫描计算和邻井相对位置测量误差计算。目前，邻井距离扫描计算方法已基本成熟，邻井相对位置测量误差计算方法尚未完善，多数学者主要研究单井井眼轨迹测量误差的计算，但是对于井与井之间测量误差的相关性研究较少。

三、邻井相对位置测量误差的计算

由于在目前常用分离系数(PSF和OSF)的计算方法中，都是通过计算参考点和比较点处合成的协差方矩阵(即合成误差椭球)来确实参考点与比较点相对位置的测量误差，同时分离系数计算方法中考虑了参考井和比较井井径的影响，因此推荐将考虑参考井和比较井井径影响的合成误差椭球的大小视为参考井和比较井相对位置测量误差的大小(如图3所示)，以便于通过计算和三维描述邻井相对位置的测量误差来优选分离系数的计算方法。

图3 邻井相对位置测量误差示意图

根据目前的井眼轨迹测量误差分析理论，在地理坐标系中各项误差源对井眼轨迹第i个测点测量误差的影响可以表示为[6]：

(2)

式中：Ni，Ei，Vi—分别表示测点在地理坐标系中的北方向、东方向和垂直方向上坐标；var(Ni,Ni)，var(Ei,Ei)，var(Vi,Vi)—分别表示北方向、东方向和垂直方向上的方差；cov(Ni,Ei)，cov(Ei,Vi)，cov(Ni,Vi)—分别表示它们之间的协方差。

假设参考井和比较井的测量误差不相关，在第i个参考点和扫描点，各项误差源对参考井和比较井井眼轨迹测量误差的总影响可以表示为：

ΣGi=ΣPi+ΣMi

(3)

计算可得总的位置不确定性的协方差矩阵ΣG的特征值σ1、σ2和σ3，以及三个特征值所对应的单位特征向量pi1、pi2和pi3。那么考虑参考井和比较井井径影响的第i个合成误差椭球的三个主半轴长ai、bi和ci可由式(4)求得：

(4)

式中:λ—允许的最小置信因子；σi1、σi2和σi3—协方差矩阵ΣGi的特征值；ri—在第i个参考点和扫描点处参考井和比较井井眼半径的和。

合成误差椭球的三个主轴方向也就是单位特征向量pi1、pi2和pi3所表示的方向。

四、分离系数计算方法的优选

优选分离系数计算方法的流程如图4所示，其中缩放后合成误差椭球的三个半轴长为合成误差椭球的三个半长轴乘以缩放系数。

图4 分离系数计算方法优选的流程

五、分离系数计算方法优选算例分析

某平台位置处的地磁场强度为50 054.5 nT，地磁倾角为46.53°，地磁偏角为4.15°。该平台上其中两口水平井(I井和P井)的井口位置间距为27.67 m，两口井设计轨道的三维示意图如图5。

图5 I井和P井设计轨道的三维示意

采用文献[7]提供的ISCWSA-MWD基础模型，取置信因子λ的值为2，计算可得垂足分离系数和定向分离系数随井深的变化如图6所示，垂足分离系数最小值为0.778，定向分离系数最小值为1.029，参考井井深大于640 m时，垂足分离系数小于1，而定向分离系数大于1。由图7可知，邻井相对位置测量误差放大1.029倍后，参考井的全井段都没有与误差椭球相交。因此，垂足分离系数的计算结果相比定向分离系数高估了I井和P井的井眼碰撞风险，钻井现场应选择定向分离系数的计算结果作为这两口井的防碰依据。

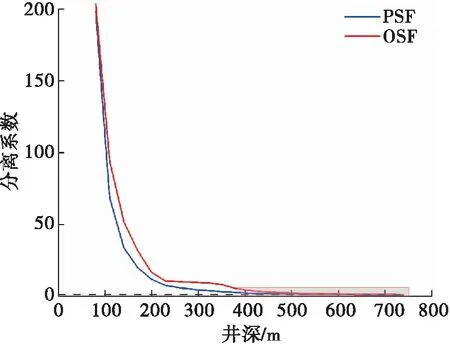
图6 垂足分离系数和定向分离系数随参考井井深的变化

图7 缩放后的邻井相对位置测量误差三维示意图

六、结论与建议

(1)在钻井工程的发展历程中，虽然分离系数的计算方法已有多种，但是这些计算方法仍有局限性，需要根据现场实际情况选择合适的分离系数计算方法，以用于科学地指导定向钻井设计与施工。

(2)通过协方差矩阵合成，考虑参考井和比较井井径的影响，建立了邻井相对位置测量误差计算模型，提出了基于邻井相对位置测量误差计算的分离系数算法优选方法。

(3)计算实例表明，相同条件下分离系数不同计算方法的结果具有较大差异，建议钻井工程中结合邻井相对位置测量误差的计算和三维可视化优选出符合实际情况的分离系数计算结果，为定向井工程实施防碰作业提供更为科学地依据。