圆形中空夹层不锈钢管混凝土短柱轴压力学性能分析

彭桂瀚，宋春生，罗慧苓，王洁

(1.福州大学土木工程学院，福建 福州 350108；2.福州理工学院，福建 福州 350506；3.渤海石油装备福建钢管有限公司，福建 福州 350512)

圆形中空夹层不锈钢管混凝土结构质量轻，抗弯刚度大，外套钢管采用不锈钢，提高了耐腐蚀性、耐火性及延性等，在建筑结构柱、桥梁桥墩与输电塔等结构中应用前景广阔。不锈钢材性不同于普通碳钢，应力应变曲线无明显屈服点和屈服平台。不锈钢管混凝土短柱轴压试验研究[1]表明，不锈钢较碳钢具备更高的延性与轴向变形能力，而且钢管局部凸出幅值更大。空心率是中空夹层结构的重要参数，通常认为大空心率的中空夹层结构承载力会低于实心结构[2-3]。Wang等[4]认为加大内钢管强度、面积可提高结构承载力。采用高强内钢管使得大空心率中空夹层结构在轻质、高承载力结构中的应用成为了可能。因此，圆形中空夹层不锈钢管混凝土结构区别于普通碳钢结构，开展有关试验研究，进行空心率等主要参数分析，对了解其结构力学性能是必要的。

现行钢管混凝土结构规范，如欧洲Eurocode 4[5]、美国AISC 360-10[6]、ACI 318-11[7]及中国GB 50936—2014《钢管混凝土结构技术规范》[8]等，适用于碳钢钢管结构，有关不锈钢管结构规程尚未颁布。因此，国内外学者开展了一些中空夹层不锈钢管混凝土结构研究工作。Han等[9]和Wang等[4，10]进行了中空夹层不锈钢管混凝土短柱试验；Han等[9]认为圆形截面碳钢简化公式计算值偏保守；Wang等[4，10]试验表明现行规范承载力计算值偏保守；Hassanein等[11-12]采用了碳钢本构模拟不锈外钢管，导致承载力有限元计算值偏小；Wang等[13]使用Han约束混凝土本构关系提高了中空夹层不锈钢管混凝土短柱有限元模型计算精度。

基于以上研究现状，本文采用Rasmussen[14]不锈钢本构模型，通过Wang等[4]试验验证，建立基准有限元模型，对结构性能主要影响参数空心率、混凝土和内外钢管强度等进行分析，提出圆形中空夹层不锈钢管混凝土结构承载力修正计算简式，同时也对现有相关国内外规程对于该结构承载力计算的适用性进行讨论。

1 基准有限元模型

通用软件Abaqus建立圆形中空夹层不锈钢管混凝土短柱构件有限元模型。其中钢管采用4结点减缩积分格式的壳单元(S4R)模拟，在其厚度方向采用9个Simpson积分点；盖板和内填混凝土采用8结点减缩积分格式的三维实体单元(C3D8R)。钢管和内填混凝土用表面与表面接触类型，切向考虑库伦摩擦，法向用硬接触模拟。

约束试件底端3个方向的线位移和角位移，约束除轴向外的2个线位移和3个方向的角位移；顶端施加竖向荷载，采用位移加载方式。考虑试验构件的对称性，计算模型取1/4短柱。网格划分后的有限元计算模型如图1所示，共计4 744个节点和3 280个单元。

不锈钢外钢管采用Rasmussen[14]推荐的两阶段本构关系；受压混凝土采用韩林海[15]提出的核心混凝土应力-应变关系；受拉混凝土本构关系采用断裂能-开裂位移的关系模型；碳钢本构关系模型采用五段式应力-应变关系曲线[15]。

钢管混凝土结构强度主要由核心混凝土提供，残余应力影响通常小于1%，初始缺陷降低方钢管混凝土强度幅度仅为1.1%～3.7%[16]。同时，考虑圆管较方管相比更不易发生局部屈曲，有限元模型忽略初始缺陷和残余应力影响，提高计算效率。

Tao等[17]进行了14根圆中空夹层钢管混凝土短柱试验；Wang等[4]进行了23根圆中空夹层不锈钢管混凝土短柱试验。限于篇幅，选取Tao等[17]试件cc4-cc7以及Wang等[4]试件AC140×3-HC22×4-C40、AC140×3-HC22×4-C80、AC140×3-HC89×4-C40、AC140×3-HC55×11-C40以验证有限元计算模型。Wang等[4]短柱试验装置如图2所示。有限元数值模拟计算各构件承载力与试验值列于表1。可见，各构件承载力有限元计算值NFE和试验值Nu比值在0.93～0.99之间，平均值为0.95，标准差为0.02。图3和图4为试验与有限元计算荷载-应变曲线。可见，2条曲线发展规律一致，吻合度较好。图5、图6分别为Wang等[4]AC140×3-HC89×4-C40试件内钢管与AC140×3-HC55×11-C40试件外钢管的试验破坏模式与有限元破坏应力云图对比图，两者破坏模式相同。综上可见，基准有限元模型可较好反映试验构件实际受力情况。

表1 有限元计算值和试验值对比Tab.1 Comparisons between test and FE results

2 有限元参数分析

考虑中空夹层圆形不锈钢管混凝土短柱构件主要结构参数空心率、混凝土强度、不锈钢外管以及碳钢内管强度等，参考目前现有相关试验研究[4]与有限元分析[13]的参数取值，开展有限元参数分析。相关计算曲线列于图7～图16。除空心率0.86的构件后期延性较差外，其余构件未见明显差别，且空心率对峰值应变无明显影响，如图7所示。当内钢管为高强钢管(屈服强度794 MPa)时，极限承载力随空心率的增大先增加后减小，空心率0.46时构件达到最大承载力1 913 kN；而当内钢管屈服强度为235 MPa时，结构承载力则随空心率增大呈非线性下降，详见图8。可见，采用高强内钢管可有效改善大空心率构件承载力低的缺陷。空心率0.16～0.86范围内，中空夹层结构极限承载力均高于实心结构(1 736 kN)，较实心结构提高幅度3%～10.2%。

空心率越大，跨中截面处外钢管与混凝土的相互作用力越小，外钢管的约束效应也越低(图9)。内钢管强度对跨中截面处外钢管与混凝土相互作用力无明显影响，如图10所示。图中由于基准模型空心率较小(0.16)，进一步减弱了内钢管作用，图中曲线出现了重合。当空心率一定时，增强内管强度对提高极限承载力有限。内钢管强度增加238%，极限承载力仅提高5.5%(图11)。从图12可知，当空心率一定时，内钢管强度对构件后期延性、峰值应变和初始刚度无明显影响。

结构极限承载力与内填混凝土强度、外钢管强度近似成正比线性关系(图14、图16)，线性关系式分别为y=11.342x+812.44和y=1.98x+1 231。混凝土强度增加200%，外钢管强度增加129%，极限承载力分别提高69%和32%。从图13、图15可见，混凝土和外钢管强度对峰值应变和后期延性无明显影响，但提高混凝土强度和降低外钢管强度会加大下降段斜率，降低结构延性，同时混凝土强度提高可使结构初始刚度增大，而外钢管强度提高对初始刚度影响则不明显。

3 结构承载力修正计算式

不锈钢对混凝土的约束效应较碳钢更强，按Han等[9]公式计算结构承载力偏小。结合有限元参数分析，修正Han公式[9]，提出适合圆形中空夹层不锈钢钢管混凝土短柱极限承载力修正计算简式，如式(1)所示。

Nu=K·[(Aso+Ac)fscy+Asifyi]

(1)

K=K1ξ2+K2ξ+K3ξχ+K4

(2)

(3)

式中：Aso、Asi、Ac和Ace分别为外钢管截面面积、内钢管截面面积、混凝土截面面积和外钢管截面内部所包含的空隙面积；fscy为不锈钢外管与内填混凝土的组合轴压强度；fyi为碳钢内管的屈服强度；fck为混凝土抗压强度标准值。

K为强度提高系数，与空心率和约束效应系数有关，如公式(2)；式中χ为空心率；ξ为约束效应系数，按公式(3)计算；K1～K4为计算系数，基于124个有限元模型参数分析结果，先后拟合空心率与提高系数K、约束效应系数与空心率关系后，分别得K1=-0.23；K2=0.71；K3=-0.24；K4=0.81。

按修正计算公式(1)对27个圆形中空夹层不锈钢管混凝土短柱构件[4，9]承载力进行计算以验证准确性，同时分别与试验值、Han计算值进行比较，结果见图17和表2。其中Nue为试验值，NHan为Han计算值，Nu为修正计算值。从图17可见，提出的修正算法计算值与试验值吻合高，且偏差小，优于Han公式计算值，可用于预测同类型结构极限承载力。

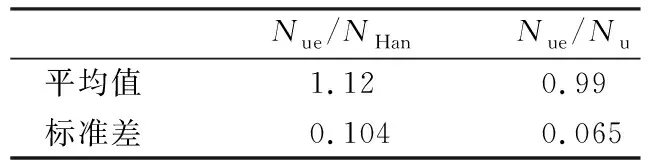
表2 修正算法计算值与试验值对比Tab.2 Comparison of calculated values by modified method and test results

4 国内外规程承载力计算

现有规范EC4[5]、AISC[6]、ACI[7]、GB 50936[8]以及Han[9]有关中空夹层钢管混凝土结构承载力公式如表3所示。以文献[4]与文献[9]共27个圆中空夹层不锈钢管混凝土短柱构件为研究对象，将承载力试验值与计算值的比值列于表4，其中Nue为承载力试验结果。可见，目前各规程承载力计算值与Han计算值均小于试验承载力，现有计算方法均偏于安全与保守。计算比值在1.07～1.23，标准差0.086～0.127。其中EC4规范计算比值1.07，偏差较小；ACI规范计算比值1.23，偏差最大。修正公式计算值和试验值最为接近。

表3 各种计算方法和相应公式Tab.3 Equations in different design codes

表4 各计算值与试验值对比Tab.4 Comparison of calculated values and test values

5 结论

1) 各研究参数对圆形中空夹层不锈钢管混凝土短柱轴压性能的影响与普通碳钢类似。外钢管、内填混凝土强度与结构承载力呈线性正比关系；碳钢内管强度对承载力提高影响较小；不同空心率下高强内钢管中空夹层结构承载力均高于实心结构，承载力随空心率增大先增后减，空心率0.46时承载力最高。

2) 提出圆形中空夹层不锈钢管混凝土轴压短柱极限承载力修正算法，计算值与试验值吻合度高，可用于预测同类型结构极限承载力。

3) 按现有规程计算圆形中空夹层不锈钢管混凝土短柱结构承载力均偏于保守。国内外相关规程、Han公式有关圆形中空夹层不锈钢管混凝土短柱结构承载力计算值均小于试验值，偏于保守；欧洲规范EC4计算值与试验值比值1.07，吻合度相对最好；ACI计算值偏差最大。