品异曲同工之妙哓思想方法之恒

顾云霞

我们仔细研读中考题，会发现有些是一类经典题型的变形，出题人改变问题背景、条件、图形等，将一些重要的思想方法巧妙地编织在题型中，从而达到“异曲同工之妙，思想方法之永恒不变”的效果。下面我们就来体验一下2019年无锡中考的第16题，感受一下“型之异，魂之恒，法之妙”。

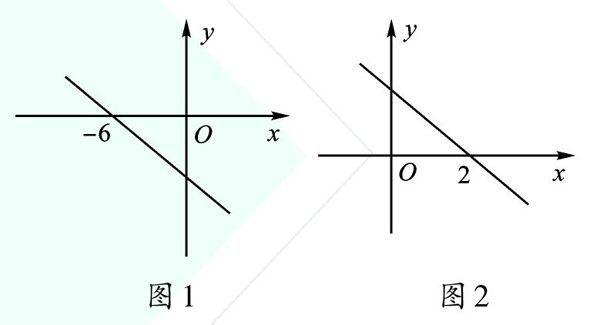
例题 （2019·江苏无锡）已知一次函数y=kx+b的图像如图1所示，则关于x的不等式3kx-b>0的解集为____。

【解析】由图像可知：k<0，b<0，一次函数y=kx+b交x轴于点（-6，0），代入得-6k+b=0，化简得b=6k;再代入3kx-b>0得3kx-6k>0，由k<0求得答案为x<2。

【点评】本题主要考查利用数形结合思想，得出一次函数与一元一次不等式的关系。具体地说，就是由函数图像上的“形”能得出哪些“数”上的关系式，再结合问题目标分析数据，运用条件解决问题。就图像上唯一的定点（-6，0），我们通常会将它代入函数关系式得到k、b的关系式，而要由它求出解集，自然又会想到消元思想。将之代入不等式消元，在解不等式的最后一步时，我们只能再回到图形中去确定“k<0”这一隐含条件，最终得解。这些自然推理便是数形结合思想和消元思想的运用——魂之恒。

【联想】（2015.江苏徐州）若函数y=kx-b的图像如图2所示，则关于x的不等式k（x-3）-b>0的解集为（ ）。

A.x<2 B.x>2 C.x<5 D.x>5

【解析】∵一次函数y=kx-b经过点（2，0），∴2k-b=0，b=2k;代入不等式k（x-3）-b>0，移项得：kx>3k+2k，即kx>5k;由图像知：k<0，∴解集为x<5。故选：C。

【点评】本题与上题有异曲同工之妙。不同的是，此题还可用整体思想求解：令t=x-3，则关于x的不等式k（x-3）-b>0的解集可变为先求关于t的不等式kt-b>0的解集。而由一次函数y=kx-b的图像可直接看出不等式kt-b>0的解集为t<2，即x-3<2，解得x<5。这真是“型之异”后的“法之妙”啊！

【变型】（2018·江苏徐州）若函数y=kx+b的图像如图3所示，则关于x的不等式kx+2b<0的解集为（ ）。

A.x<3 B.x>3 C.x<6 D.x>6

【解析】由图像可知：一次函数y=kx+b经过点（3，0），且k<0，b>0。将点代入解析式可得3k+b=0，则b=-3k。∵kx+26<0，∴ kx-6k<0，即kx<6k。又∵k<0，∴x>6。故选：D。

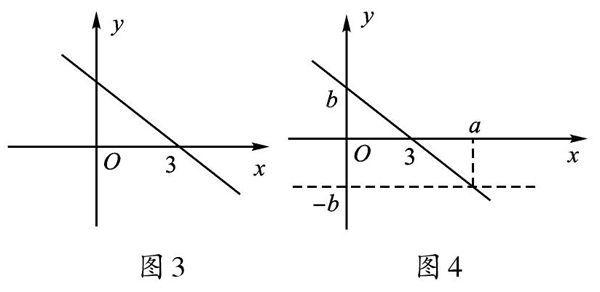
【亮点】本题亦能体现出异曲同工之妙，但还有一个妙法：可将kx+2b<0转化为kx+b<-b，它的解集也就是一次函数y=kx+b的图像在直线y=-b图像的下方时所对应的x的取值范围，如图4所示。由图像可看出解集为x>a（a>3），因此答案只能选D。

通过这类中考题的体验，我们感受到在学习函数时要重视数形结合思想、转化思想、整体思想和消元等思想的综合运用，让“数”插上翅膀，让“形”更具形象，让“法”更加奇妙，让“数学思想之魂”永恒不变，从而快捷简便地解决数学问题。

同类练习：

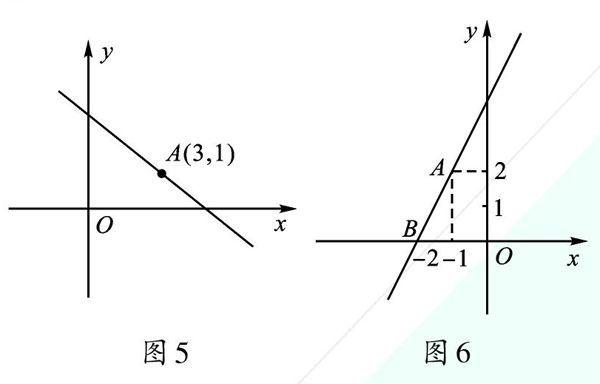
1.（2019·山东滨州）如图5所示，直线y=kx+bk<0）经过点A（3，1），当kx+b<1/3x時，x的取值范围为______。

2.（2014.湖北鄂州）如图6所示，直线y=kx+b过A（-1，2）、B（-2，0）两点，则0≤kx+6≤-2x的解集为____。

参考答案：1.x>3;2.-2≤x≤-1。