数形结合 化难为易
孙洁

初中数学学习中,“数形结合”是非常重要的数学思想方法。借助数形结合思想,使抽象问题变得直观,往往能够化难为易,豁然开朗。下面,我们以2019年中考题中与平面直角坐标系有关的“坐标点”的问题为例,感受数形结合的奇妙!
考点1 点的坐标
(2019.江苏常州,第14题)如图1,平面直角坐标系中,点P(-3,4)到原点的距离是____。
【解析】本题考查了平面直角坐标系中的点到原点的距离问题,可作出图形,过P点作x轴的垂线,利用勾股定理可得其到原点的距离为5。
【点拨】对于平面直角坐标系内点的变换问题,一定要先画出平面直角坐标系,根据坐标,找出“关键”点,仔细观察图形,问题便能迎刃而解。
考点2用有序实数表示物体的位置
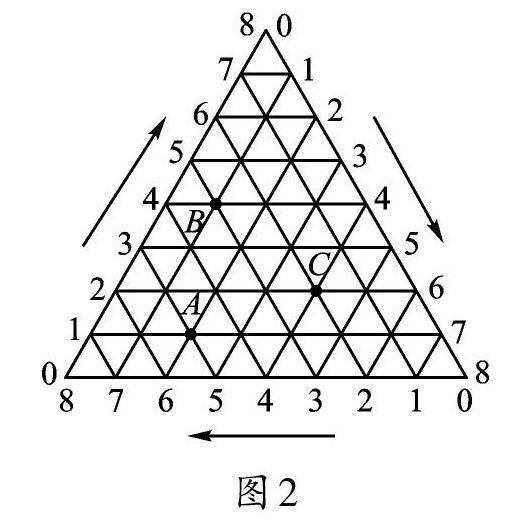
(2019.江苏连云港,第15题)如图2,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系。在建立的三角形坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(4,1,3)。按此方法,则点C的坐标可表示为____。
【解析】本题考查如何用有序实数来表示点的位置。观察点A,发现过点A的线段有三条,从水平方向开始,按顺时针方向,这三条线段的端点数分别是1、2、5,故点A的坐标可表示为(1,2,5);类似地,按照题目的规则,从水平方向开始,按顺时针方向,点C的坐标可表示为(2,4,2)。
【点拨】平面直角坐标系是用一对有序实数描述平面内物体位置的工具。类似地,我们还可以建立“三角形”坐标系,用三个有序实数来描述点的位置,也可以用角度和距離来描述点的位置……
著名数学家华罗庚先生说过:数缺形时少直觉,形少数时难入微。数形结合百般好,隔离分家万事休。平面直角坐标系就是架起数与形的一座桥梁,请同学们试一试:
1.在平面直角坐标系内,以原点为旋转中心,把点P(-3,4)旋转90°,得到点Q,则点Q的坐标是____,
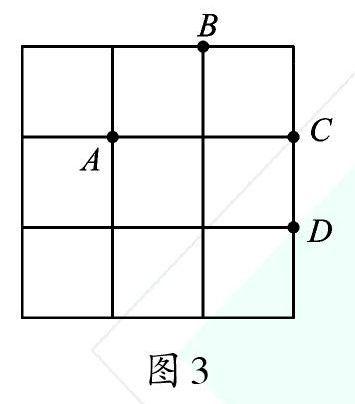
2.如图3,在3x3的正方形网格中有四个格点A、B、C、D,以其中一点为原点,以网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是____。
参考答案:1.(-4,-3)或(4,3)
2.B。

