一种改进的PSO人脸识别算法研究
林志谋
(厦门海洋职业技术学院)
0 引言
人脸识别技术是图像模式识别与计算机视觉领域中很重要的一个研究课题, 它在人工智能,机器学习,生物识别、安全监控、数码设备、商业贸易等领域都有着非常广泛的应用.中国外学者研究出了很多优秀的人脸识别算法,比如Turk等提出的PCA算法[1],基于模板匹配的方法[2-3],基于子空间分析的算法[4],还有基于无监督学习的特征LearningDescriptors算法[5],GaborFace、LBPFace算法[6],以及SRC算法[7]等.Hasan等人提出了基于PCA与SVM联合的算法[8],但是精度不够高,文中提出了一种改进的双曲正切函数PSO算法进行SVM参数寻优,同时联合PCA和SVM进行人脸识别的算法,加快了算法的收敛速度.实验结果表明该算法比其他算法有较高的识别精度,有更好的实际应用前景.
1 主要算法原理
1.1 PCA算法主要原理
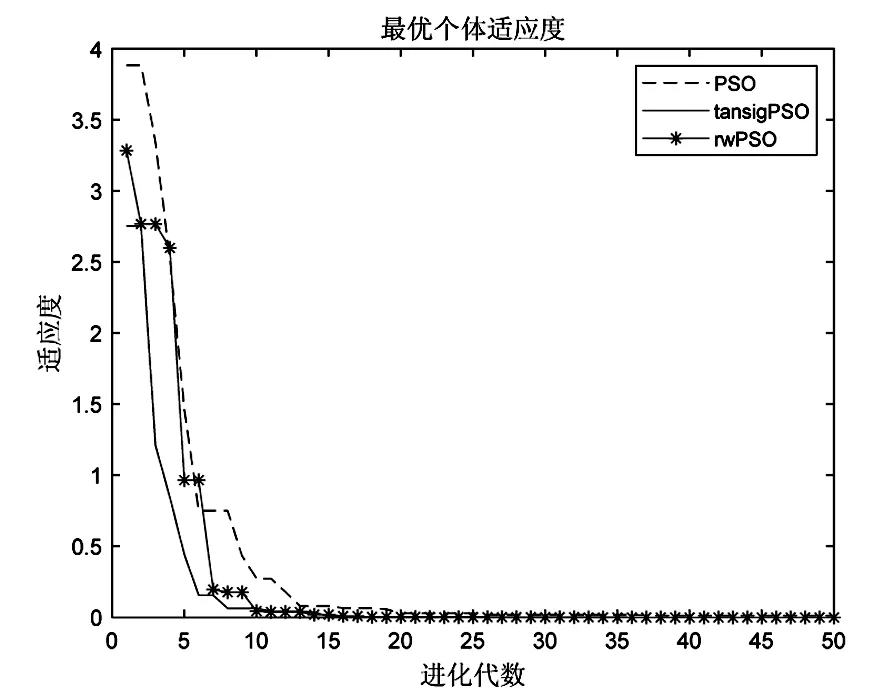
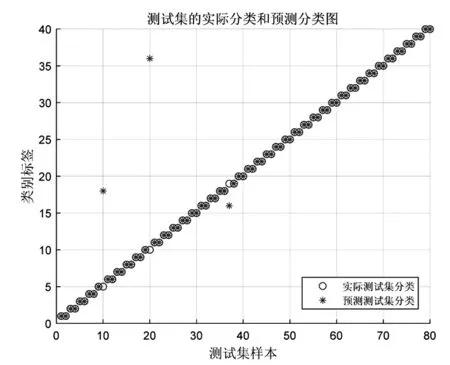
PCA(Principal Component Analysis),即主成分分析方法[9],PCA的思路是尽量减少数据集的维数[10],同时保持数据集对方差共享最大的特征.利用PCA变换可以较大幅度地降低人脸数据特征的维数,减少图像中冗余的信息和噪声,又能保留有效的识别信息.假设有n个d维空间中的样本x1,x2,…,xn,其中xi=(xi1,xi2,…,xid)TRd,假设X为这n个样本构成的数据矩阵,即X=(x1,x2,…,xn).假定需要降到m维,即给定m (2)假设协方差矩阵为S,计算公式为: (3)计算协方差矩阵S的前m个最大特征值,对它们按大小进行排序,即λ1≥λ2≥…≥λm,ψ1,ψ2,…,ψm,ψj(j=1,2,…,m)∈Rd为它们对应的特征向量,由它们构成的矩阵φm=(ψ1,ψ2,…,ψm). 利用PCA算法降低了人脸数据的维数,接下来就可以利用SVM算法,对提取得到的人脸数据进行分类处理,就可以确定每个人脸图像的身份. SVM(Support Vector Machines),即支持向量机,它的主要原理是把数据映射到一个高维空间上,使数据变稀疏,比较容易找到一个分割面来将数据分类,而这个高维的分割面就是超平面.SVM算法的主要目的是找到一个使得数据点离这个超平面尽可能远的超平面,通过这个超平面进行分类的的效果才会好.人脸识别是典型的非线性支持向量机分类问题,分类的主要流程如下[11]: 假设输入的训练数据用T表示,T={(x1,y1), (x2,y2),…,(xm,ym)},其中xi∈Rn,yi∈ {-1,1},i=1,2,…,m,步骤如下: (1)选择核函数K(xi,yi)和惩罚参数C,构造并求解最优化问题: 0≤αi≤C,i=1,2,…,m 使用二次规划法,求得最优解: (2)计算求向量w*和截距b*,w*可以通过下列式子求得: b*可以通过满足下列式子的样本求得: (3)这样就可以得到最优分类面函数: f(x)=sgn{(w*·x)+b*} 常见的SVM参数选择方法主要为梯度下降法和网格算法[12],但这些方法有些缺陷,比如寻优速度慢或者容易获得局部最优解,而采用粒子群优化算法(PSO:Particle Swarm Optimization)则可以克服这些缺陷. PSO算法[13]具有如下优点:实现比较容易,有较好的准确度,可以快速收敛.PSO算法首先在D维搜索空间中[14],随机生成N个粒子的初始种群,各个粒子有各自的初始位置并且以一定的速度飞行.假设第i个粒子的位置用xi表示,速度用vi表示,个体极值用pi表示,群体极值用pg表示.通过下面的两个公式,PSO算法可以调整粒子本身的位置和速度: vid=ω·vid+c1r1(pid-xid)+c2r2(pgd-xid) xid=xid+vid 其中c1,c2为学习因子,r1,r2为[0,1]范围内的均匀随机数,ω为惯性权重,i=1,2,…N;d=1,2,…D. PSO算法可以通过增大惯性权重数值可以提高算法的全局搜索能力,减少惯性权重数值可以提高算法的局部搜索能力.要避免陷入局部最优同时实现高效搜索的目的,必须设计合理的惯性权重.文中引入了一种改进的双曲正切函数算法来设计合理的惯性权重. 传统的PSO算法中惯性权重ω一般是随着迭代次数线性递减, 但是经过研究发现,在迭代的过程中,迭代次数t较小的时候,ω的调整一般希望能够使粒子早期具有比较强的全局搜索能力,这就要求ω应该在初始迭代的时候缓慢减少;迭代次数t逐渐变大的时候,为了获得快速的收敛速度,ω的调整应该是减小的速度要加快;迭代次数很大的时候,ω的调整一般希望能够使粒子后期具有比较强的局部搜索能力,这就要求ω应该在后期迭代的时候也缓慢减少[14].传统的线性递减的惯性权重ω显然无法满足要求,于是文中提出了一种采用改进的双曲正切函数算法来设计满足要求的惯性权重ω.为了便于表述,引入如下定义: 定义1 双曲正切函数定义为如下公式: 定义2 改进的双曲正切函数定义为如下公式: 式中k为陡降调整因子,t是当前的迭代次数,Tmax为迭代的最大次数. 定义3 改进的双曲正切函数的惯性权重ω定义为如下公式: 式中ωmax为最大惯性权重,ωmin为最小惯性权重.ω随t变换如图1所示. 图1 权重ω随t变换图 图中ωmin=0.6,ωmax=0.8,陡降调整因子k=5,Tmax=50.从图中可以看出,前期惯性权重变化缓慢,可以提高前期的全局搜索能力;中期惯性权重变化加快,可以提高中后期收敛的速度;后期惯性权重变化又趋于平缓,可以提高后期局部搜索能力.上述参数可以满足该次SVM参数算法优化的需求 改进的双曲正切函数的PSO算法的优势决定了它可以用来对SVM参数进行优化.算法的主要流程如图2所示. 图2 改进的PSO优化SVM参数算法流程图 文中使用Matlab软件,采用Ackley测试函数对改进的双曲正切函数的PSO算法(tansigPSO)的性能进行测试,并和标准的PSO算法、随机权重算法rwPSO[15]做比较,三个算法的相关参数保持一致,具体设置如下:最大迭代次数设为50,种群规模为30,各算法分别独立运行50次.得到最优个体适应度结果如图3所示,采用tansigPSO算法比其他两个算法有更强的全局搜索能力和更快的收敛速度,它有效的改善了标准PSO算法容易进入局部最优,收敛速度慢的缺点. 图3 改进的双曲正切的PSO算法最优个体适应度 为了验证文中提出的改进的基于改进的双曲正切函数的PSO算法参数寻优,同时联合PCA和SVM进行人脸识别的算法的性能,文中利用Matlab软件进行仿真测试.台湾大学林智仁教授等开发设计的集成库LIBSVM[15]内置了训练函数和预测函数,可以用它来实现SVM算法.文中采用ORL人脸库来进行算法验证,文中把它们分成两组,用前8张人脸图片作为SVM模型训练样本,后2张图片作为SVM模型预测的样本,算法的主要流程如下: (1)读入ORL人脸库所有的图片,分别用作训练样本和预测样本. (2)利用PCA算法对人脸数据库的训练样本降维并且提取人脸图像的特征向量. (3)SVM参数的优化采用改进的双曲正切函数的PSO算法,从而得到SVM参数的最优解. (4)把第2步得到的人脸图像的特征向量和第3步得到参数的最优解,输入到SVM分类器中进行训练识别. (5)利用PCA对人脸测试样本进行特征降维,提取人脸图像的特征向量,然后输入SVM测试函数中. (6)比较SVM测试函数产生的标签和预测样本的人脸图片的标签,得到人脸识别的准确率. 利用改进的双曲正切函数PSO算法对LIBSVM人脸识别模型进行参数优化的适应度收敛曲线如图4所示,最大进化代数为200,采用高斯核函数RBF作为SVM的核函数.可以得到最优参数为惩罚系数c=0.082963,核函数参数g=0.01.利用tansigPSO算法寻找得到的最优参数训练LIBSVM模型,在利用人脸图像训练集进行训练的过程中人脸识别的精度为96.25%. 图4 改进的tansigPSO算法的适应度曲线 然后再利用训练好的模型对人脸数据库图像的测试集进行预测,预测错误有3幅图像,预测的精度也为96.25%,如图5所示. 图5 人脸图像测试集的实际分类和预测分类图 文中算法(tansigPSO +PCA+SVM)与其他算法精度比较见表1,常规的PCA+SVM算法识别精度为93.5%,文献[16]采用KICA+SVM的识别方法,识别精度为93%,文献[17]采用KICA和Relief人脸识别算法,达到的识别精度为91.4%.与这些算法比较,文中提出的算法识别精度更高,达到了96.25%,明显优于其他算法. 表1 文中算法与其他人脸识别算法精度比较 文中采用改进的双曲正切函数的PSO算法获得SVM分类模型的最优参数,再联合PCA算法和SVM算法对人脸进行识别,具有较高的准确率.在模型预测精度达到了96.25%,明显优于常规的PCA和SVM联合的算法,表明运用改进的双曲正切函数的PSO算法确实提高了模型在人脸识别上的精度,加快了算法的收敛速度,增加了可操作性,具有较为广阔的应用空间.
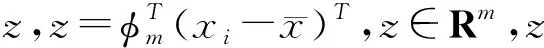
1.2 SVM算法主要原理
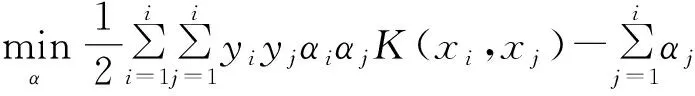

2 改进的PSO优化算法和SVM参数寻优
2.1 PSO算法
2.2 改进的双曲正切函数的PSO算法和SVM参数寻优


3 文中算法的主要流程
4 实验结果和分析
4.1 文中算法性能测试

4.2 与其他人脸识别算法比较

5 结束语

