基于AHP的基金资产配置策略分析*

徐 惠，闫云侠，朱家明

(安徽财经大学)

0 引言

随着改革开放程度的不断提高，中国经济运行中的各种风险逐渐暴露并集中传导和体现于金融领域.党的“十九大”报告提出“守住不发生系统性金融风险的底线”要求，并将防范化解重大风险看成决胜全面建成小康社会三大攻坚战的首要战役.作为金融系统的重要组成部分的资产管理业务的风险状况同样是中国金融体制改革过程中值得关注的问题.因此，中国人民银行于2018年出台了《关于规范金融机构资产管理业务的指导意见》，旨在规范金融机构资产管理业务，有效防控金融风险，引导社会资金流向实体经济，更好地支持经济结构调整和转型升级.公募基金是最具代表性的资产管理业务形态.由于采取相对绩效考核制度，竞争压力使得公募基金资产配置变得非常复杂，持股集中度也相对较高，成为影响系统性风险的潜在因素.因此如何平衡基金投资收益和系统性风险之间的关系值得深入探究.

目前国内学者关于投资风险的研究有很多，一是研究投资品种和方法的多样化.廖赋翰通过研究金融数学中期望和方差的关系，对证券投资组合的风险与收益进行了分析[1]；张丽娟运用VaR模型中方差-协方差法对保险投资风险进行了度量[2]；张夏洁等运用随机微分泛函变分法，研究了股价服从Levy过程的投资组合优化策略[3]；郭文旌等运用均值-方差对投资者的最优时间一致性资产配置进行了分析[4]；周亮基于BEYR研究了动态资产配置策略[5].二是研究股票投资风险的角度多元化.傅毅等运用动态规划原理，对我国A股市场2016年3月份的"中国太保"和"国海证券"进行了策略的情景模拟，得到相应的最优资产配置策略[6]；陈倩等追踪市场指数对投资组合策略进行相关性检验的回归分析[7]；刘小茂等对深市股票的VaR与CVaR进行了对比研究[8].拟运用聚类分析和层次分析法研究基金资产配置的策略问题.

1 数据来源和假设

该文数据来源于2020年“五一”大学生数学建模竞赛.为便于解决问题，该文的研究过程和结论均建立在以下假设成立的基础上：(1)基金公司进行投资期间，社会政策无较大变化经济发展形势较稳定；(2)基金公司进行投资期间，无不可抗力等导致的重大事件的发生；(3)基金公司投资期间所花费的交易费等其他费用不计，只考虑单纯的本金和收益关系；(4)不存在无风险资产，每种股票的收益与否相互独立；(5)基金公司仅依靠预期的投资风险和收益来做出投资决定；(6)基金公司在年初投资股票，年末获得收益，所选股票在决策期间发生的变化不会影响投资决策，即投资期间不会随机撒资或追加投资；(7)基金公司都是遵循占优原则的，即在同风险水平下，选择收益率较高的股票，在同收益率水平下，选择风险较低的股票；(8)股票预期收益率变化是符合正态分布的.

2 基于聚类分析的资产配置策略度量模型

2.1 研究思路

由于附件1给出的10家基金公司的部分资产配置数据是静态的，所以无法确定各个基金公司在2019年度的收益情况和各个股票的风险情况，但可以得到股票的每股单价和各个公司中这部分股票市值占公司总市值的比例等信息，通过聚类分析，可以度量不同基金公司之间资产配置策略的相似性和不同.

2.2 研究方法

2.2.1 资产配置策略分析

通过对附件1的数据进行分析，已知各基金公司中每种股票的持股总市值为mi万元，持股总量为ni万股，则易得到各种股票的单价为vi.

对各基金公司拥有的各个股票的总市值进行累加可以得到每家基金公司的总市值M.

对比各家基金公司，结果如图1所示.

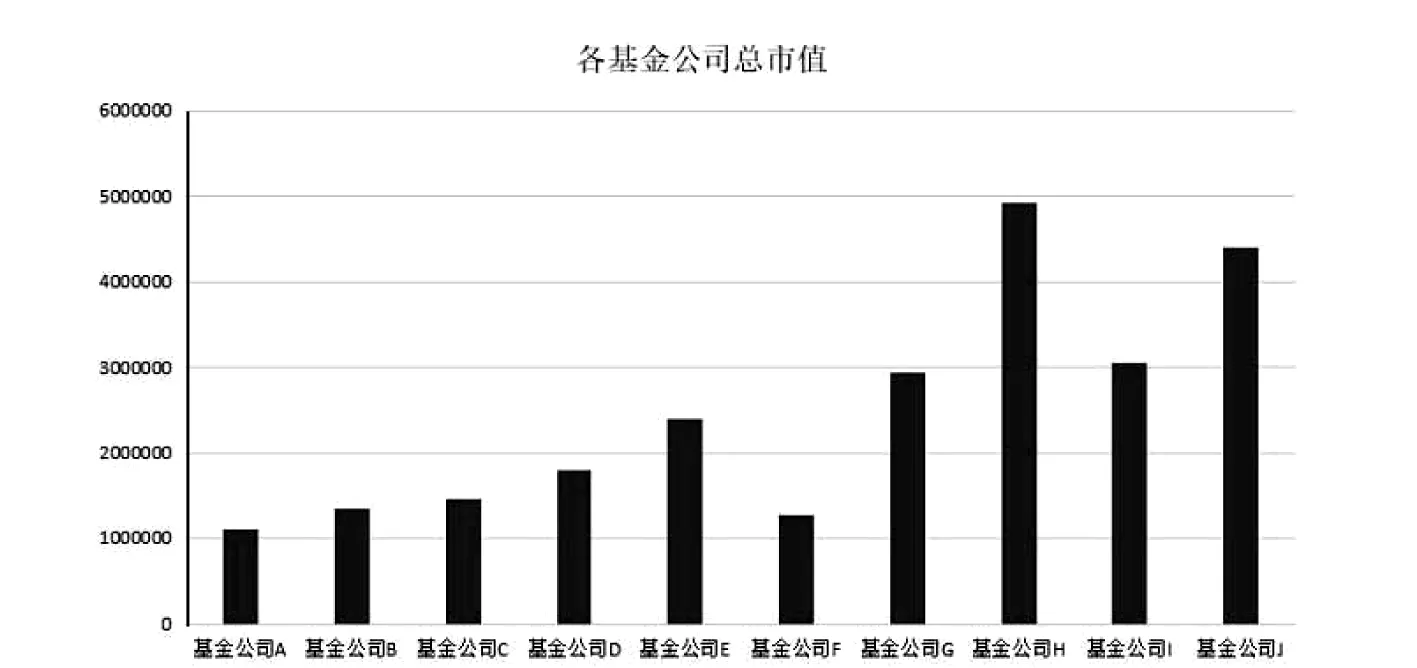
图1 各公司总市值

另外，可以通过公式(3)得到基金公司的各个股票持股总市值占公司总市值的百分比Pi：

例如， 基金公司A、B各个股票持股总市值占公司总市值的百分比视图如图2所示.

图2 基金公司A和基金公司B各部分股票市值占比

通过对百分比视图分析，各公司持有的10支股票的总市值占比相对比较均衡.尽管不同公司购买的股票种类不同，但是从总体上看基金公司购买的股票类型与其总市值占比存在相似性.

2.2.2 资产配置策略度量模型

基于自身股票占比平衡及不同基金公司股票占比存在相似性的特点，建立基于基金公司自身股票占比特点的资产配置策略度量模型为

其中ER是基金公司自身各股票均衡度，ER值越小表示该公司各个股票总市值越均衡.将各个公司股票持股总市值占公司总市值的百分比Pi代入公式，得到10家公司的自身各股票均衡度ER分别为 0.0198，0.0208，0.0239，0.0242，0.0414， 0.0427， 0.0452，0.0457， 0.0527，0.0739.

2.3 结果分析

结果显示，3类基金公司的股票总市值占比存在相似性.基金公司A、基金公司B、基金公司C自身各股票均衡度较为相似，且各个股票总市值比较均衡.其次是基金公司D、基金公司E、基金公司F、基金公司G和基金公司H的自身各股票均衡度较为相似，并且总体来说均衡度较前三家基金公司稍微差一点.最后是基金公司J，其均衡度RJ=0.0739，可以说相对于其他几家基金公司，基金公司J的各股票总市值分布有些不均，即更加激进一些，如图3所示.

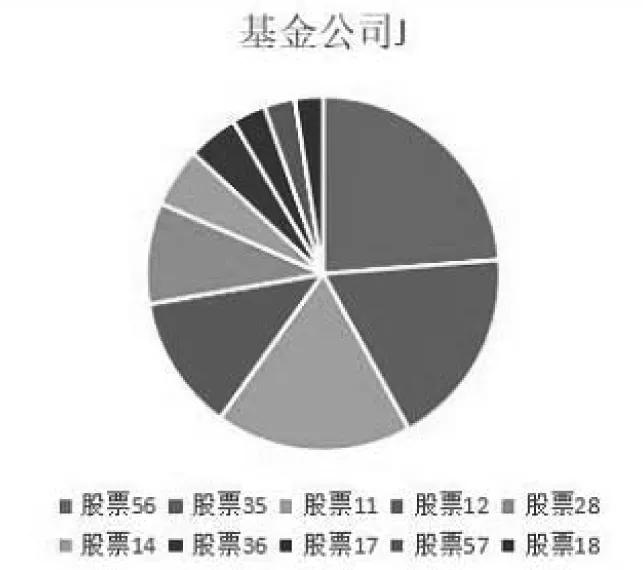
图3 基金公司J各部分股票市值占比

根据图3可以很明显的看出，基金公司J的各个股票总市值分布差别明显，正好对应前面分析得到的基金公司J的各股票总市值分布有些不均的结论.

2.4 基于手肘法的模型检验

采用kmeans最优k值的确定方法-手肘法[9]进行聚类分析，检验模型的正确性.在手肘法中，随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小，即

其中Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心(Ci中所有样本的均值)，SSE是所有样本的聚类误差，代表了聚类效果的好坏.当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状(如图4所示)，而这个肘部对应的k值就是数据的真实聚类数.

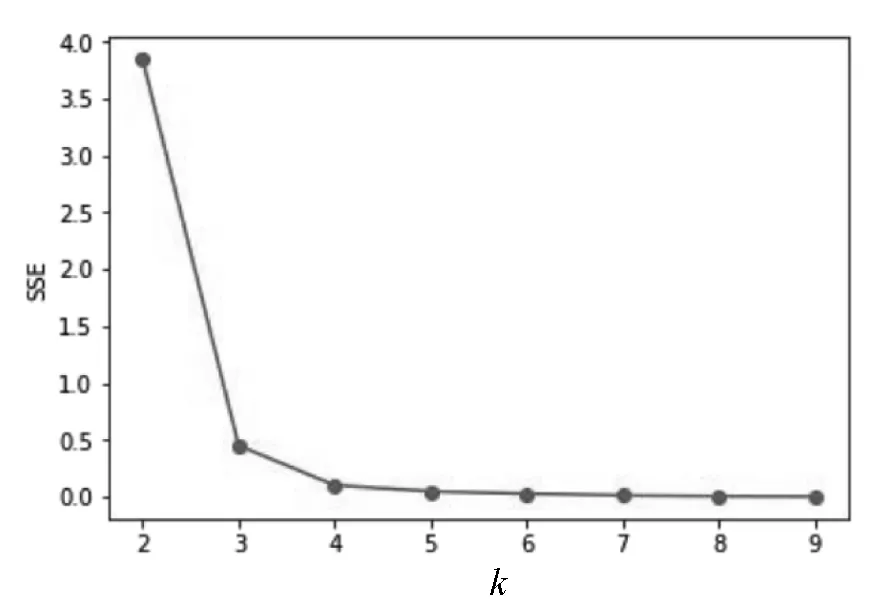
图4 SSE和k的关系图

显然，肘部对于的k值为3(曲率最高)，故对于这个数据集的聚类而言，最佳聚类数应该选3，运算的结果为[2 2 2 0 0 0 0 0 0 1]，也就代表着分为三类，此结果与构建的资产配置策略度量模型分析结果相同.

3 基于AHP的资产投资组合模型

3.1 研究思路

投资收益率的高低及投资风险的大小是基金公司在股票投资时最关心的两个问题.股票投资组合管理的目标是实现效用最大化.由于投资的收益率受证券市场波动的影响，因而可以将其看作一个随机变量.根据附件2提供的2019年样本股票价格数据，将每支股票按月划分计算出收益率X，根据X的期望值E(X)来衡量该种股票投资的获利能力，期望值越大，股票的获利能力越强；股票的风险则用该种股票投资收益率的方差D(X)来衡量，方差越小，投资的风险越小[10].

由于每个基金公司股票投资组合数均为10，所以在此也将从中选出10只股票来进行组合投资.为了合理分配投资资金，可以通过层次分析法计算出每支股票的权重，根据权重乘以总投资额，即得该股票的投资金额，从而确定最终的股票投资组合方案.

3.2 研究方法

3.2.1 均值-方差模型

首先根据获得的股票单价，通过对比发现各股票的单价大约为2019年12月底左右的股票单价.而附件2的原始数据中一些股票缺少部分数据，在建立模型之前首先要对缺失数据补全.采用SPSS工具，分析股票变化过程，研究相近几日的股票单价变化和整体的关系，采用最近7 d线性趋势预测的方式，将全部的缺失数据进行补全.然后利用附件1中的股票价格对补全的效果进行检验，经检验，左右股票的误差均在7.02%的范围内，说明缺失值补全效果良好.

为了使选择的股票更具有代表性和说明性，将附件2中提供的一整年的数据按照月份进行划分，同时为了达到最大收益率，按照每只股票在每月最低价时买入，再以最高价卖出这种情况来计算其每月的收益率.可以计算出每只股票每个月份的收益率βj.

其中a为每支股票每月份的最高价，b为每支股票每月份的最低价.

同理，可以求出每支股票所有月份的收益率，取其平均值，得到每支股票收益率的期望E(Si).

根据每支股票每月的收益率βj及其期望E(Si)，可以计算出方差(风险系数)D(σi).

根据每支股票收益率的期望E(Si)和方差D(σi)，计算变异系数CV，度量股票的相对风险.

其中，CVi表示第i支股票的变异系数.

根据建立的模型，运用Excel来完成，从而得到这57支股票数据处理后的期望收益、标准差以及变异系数，部分结果见表1.

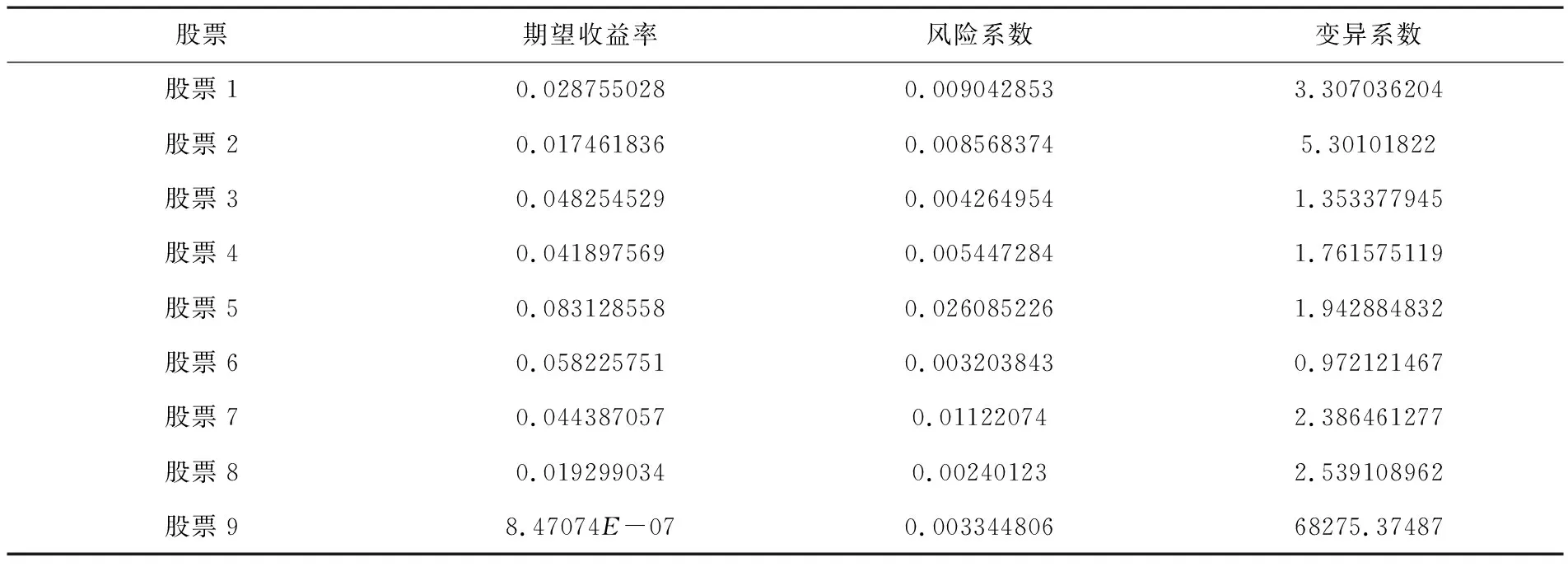
表1 股票的期望收益、风险系数、变异系数

根据变异系数对股票进行由小到大排序：若CVi<0，表示近些年该股票的收益下降，故排除.若CVi>0且CVi→1，表示该股票变异特性弱，风险小，收益率高.由此，可以看出股票23、股票6、股票41、股票49、股票14、股票12、股票26、股票3、股票32、股票48可以作为股票投资进行组合.

3.2.2 AHP模型

为了实现投资效用最大化的目标，建立层次分析模型，即AHP模型.将方案的选择分为三层，形成一个递阶层次结构如图5所示.第一层为目标层表示选择最优的股票投资组合，第二层为准则层表示投资的倾向，第三层为方案层表示所选的股票.依据投资效用最大化的目标对这三个层次相互比较判断进行综合分析，最终确定10支股票的投资比例[11].

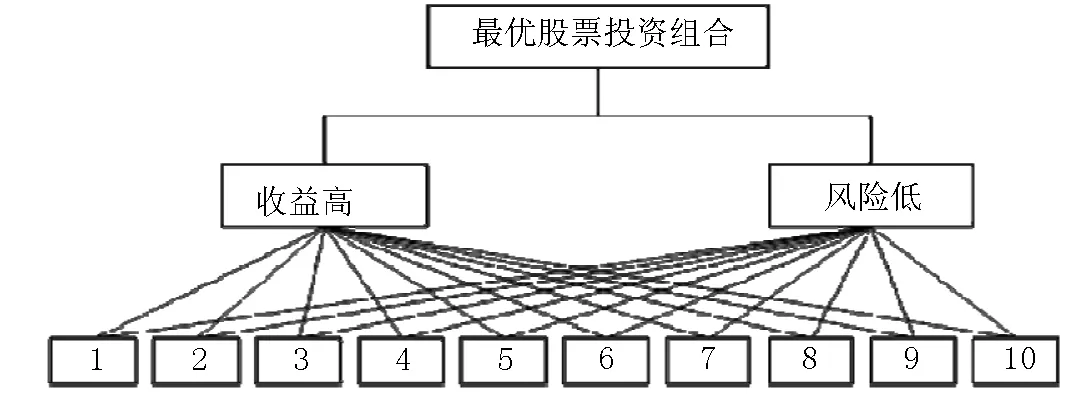
图5 层次结构图

方案层中1-10分别表示上述选出的10支股票，见表2.

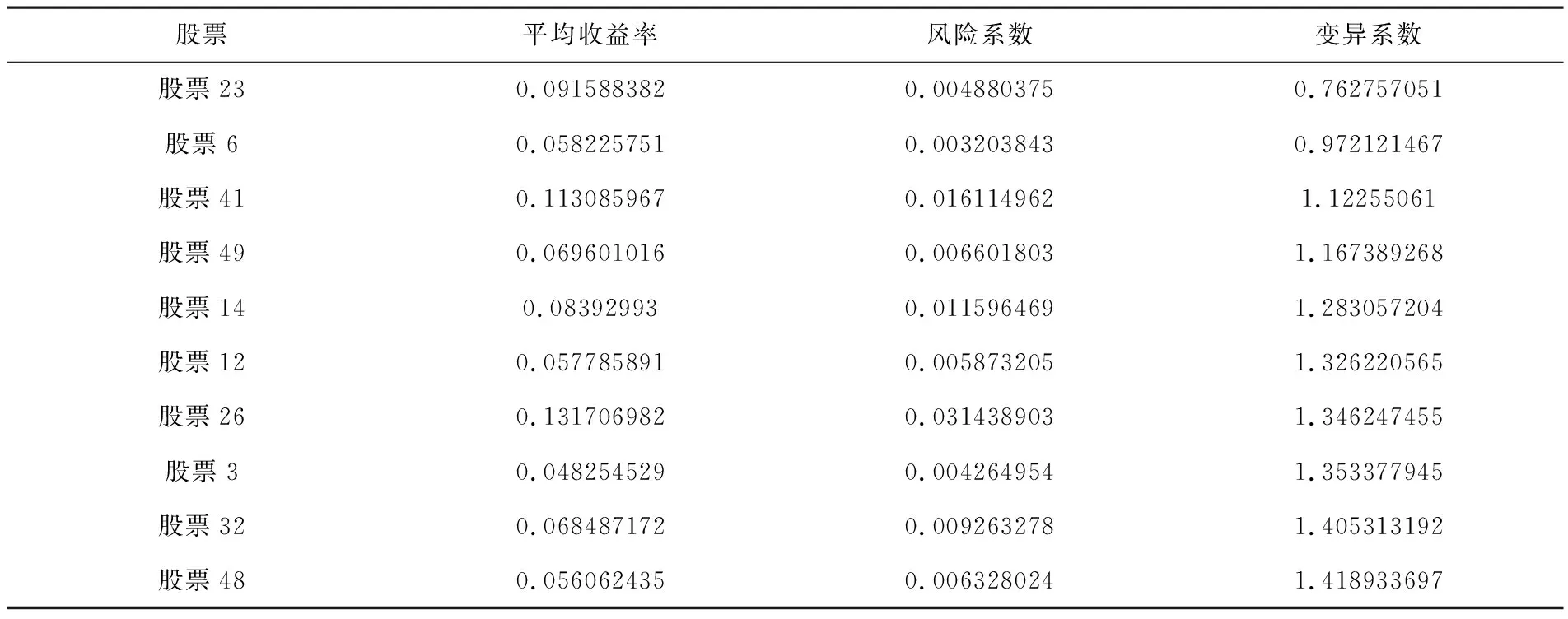
表2 选出的10支组合投资股票

首先根据准则层对方案层的股票进行赋权[12]，赋权则由统计数据得到的收益、风险比重，由此得到一个比较判断矩阵(正互反矩阵).

可求出最大特征值λmax=2，对应的特征向量经过归一化得W=[0.2728 0.7272]就是准则层对目标层得排序向量.

用相同的方法，给出第三层(方案层)对第二层(准则层)的每一准则比较判断矩阵F1、F2:

由此求出各排序向量(最大特征值所对应的特征向量归一化)：

最后，将由各准则层对目标的权向量W和各方案对每一准则的权向量，计算各方案对目标的权向量，称为组合权向量.组合权向量如下：

根据矩阵乘法可得

K=P·W=[0.2169 0.1022 0.1216 0.06751 0.0550 0.0903 0.0903 0.1344 0.0559 0.0960]T

所有基金的持股市值总和M为24675114.49，应用python编程[13]计算各股票的最佳投资比例见表3.

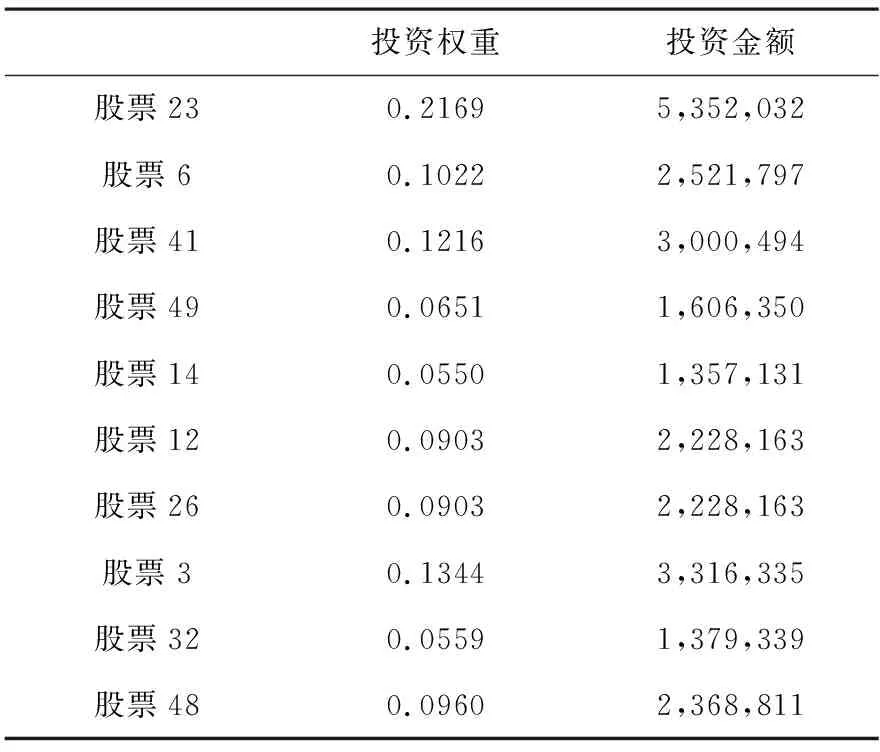
表3 10个股票的投资比例

4 结果分析

由表3得各个股票的最佳投资比例，股票23的投资比例为0.2169，投资金额为5,352,032元；股票6占比0.1022，金额2,521,797元；股票41占比0.1216，金额3,000,494元；股票49占比0.0651，金额1,606,350元；股票14占比0.0550，金额1,357,131元；股票12占比0.0903，金额2,228,163元；股票26占比0.0903，金额2,228,163元；股票3占比0.1344，金额3,316,335元；股票32占比0.0559，金额1,379,339元；股票48占比0.0960，金额2,368,811元.由此获得基金公司资产配置的最优策略.

5 结束语

首先，根据各基金公司购买的股票类型及其总市值占比存在相似性，建立资产配置策略度量模型，并运用聚类分析来检验模型是正确的.接着，分析数据，采用均值-方差算法对每支股票排序，得出收益率较高的前 10 支股票， 分别是股票23、 股票6、股票41、股票49、股票14、股票12、股票26、股票3、股票32、股票48.然后，将这10支股票作为投资组合的样本，求得其在投资效益最大化下的权重和投资金额，获得资产配置的最优策略.