基于Anscombe变换的X射线图像序列盲源分离降噪
沈 帆,李翰林,孙 斌,喻春雨*
(1.南京邮电大学 电子与光学工程学院、微电子学院,江苏 南京 210023;2.南京邮电大学 自动化学院,江苏 南京 210023)
1 引 言
自1895年X射线被发现以来,X射线成像技术被广泛应用于工业、医疗等领域[1]。由于泊松噪声是影响X射线图像质量的主要因素,因此研究泊松噪声的消除方法及性能提高一直是恢复X射线图像质量的有效途径[2-3]。在此方面较为典型的研究有:Selesnick等人提出非高斯双变量分布,通过贝叶斯理论导出非线性阈值函数[4],并结合隐马尔科夫模型实现对泊松噪声进行滤除[5];Ma,LY等人将图像的稀疏表示用于图像恢复,基于像素总变差正则化和数据保真度获得泊松噪声统计,从而滤除泊松噪声[6]。此外,近年来还有对X射线图像进行Anscombe变换,将图像中泊松噪声变换为高斯噪声,然后利用相对成熟的高斯噪声降噪算法对其进行降噪[7],如:Manduca等人提出将Anscombe变换结合双边滤波方法应用于低剂量CT投影数据降噪[8];毕一鸣等人提出通过Anscombe变换和三维块匹配(Block-Matching 3D,BM3D)滤波相结合进行降噪,最后用滤波反投影算法重建图像[9]。
由于图像中信号和噪声被视为不相关分量,则基于盲源分离(Blind Source Separation,BSS)理论,将含噪声图像看作信号分量和噪声分量的组合;而且通过Anscombe变换可以将泊松噪声转化为高斯噪声进行消除,由此提出基于Anscombe变换的X射线图像序列盲源分离降噪方法(以下称本文降噪算法),其算法思想是:首先取一序列X射线图像,并利用Anscombe变换将图像中泊松噪声变换为高斯噪声;然后将含噪声图像视为信号分量与噪声分量的混合,通过非线性主分量分析(Nonlinear Principal Component Analysis,NLPCA)[10]对图像序列进行BSS运算;在分离分量中取方差较大的进行Anscombe逆变换,得到降噪图像。
2 本文降噪算法介绍
首先获取一个X射线图像序列,该序列包含至少2张图像,然后对每张图像进行Anscombe变换;将图像中泊松分布噪声转化为高斯噪声。Anscombe变换是Anscombe于1948年提出的一种从泊松分布转到近似高斯分布的非线性变换方法[11-12],如式(1)所示:
(1)
其中:x服从泊松分布,x′是近似服从方差为1的高斯分布。
通过式(1)产生一组新的含噪声图像序列。将每张图像视为一个观测信号,则该含噪声图像序列视为多个观测信号;每个观测信号是噪声分量与图像信号分量的混合,因此可以用BSS处理将图像信号分量从噪声中分离出来[13]。分离之后得到的是初步降噪图像,要通过Anscombe逆变换才可以得到最终降噪图像。这里采用NLPCA进行BSS处理,是因为主分量分析(Principal Component Analysis,PCA)用一系列直线来描述数据中的主要变化趋势,而NLPCA使用若干开放曲线或闭合曲线来描述数据变化趋势,更适合描述图像中信号和噪声之间的关系[14],其优化条件如式(2)所示:
(2)
其中:wiTx′为非线性因子,g(x′)是非线性函数,其表达如式(3)所示:
g(x′)=x-G(x′)+G(ν),
(3)
其中:ν为高斯随机向量,取G(x)=tanh(ax),a为一常数。
假设W是一个正交矩阵,令S=Wx′,则用于优化的指标函数如式(4)所示:
(4)
其中:算法采用非线性递归最小二乘学习规则[15],它根据输入精度数据自动决定适合的学习速率参数,具有比随机梯度方法收敛快的优势[16]。
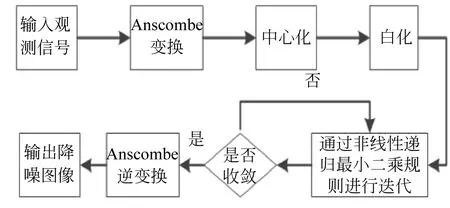
图1 本文降噪算法流程图
图1为本文降噪算法的流程图,算法流程依次为:对X射线图像序列中图像进行Anscombe变换;通过NLPCA对Anscombe变换后含噪声图像进行BSS处理,得到初步降噪图像;进行Anscombe逆变换,得到最终降噪图像。由此制定算法步骤如下:
Step 1:利用X射线成像设备拍摄一组图像序列,所拍摄目标与场景相对静止,采样张数为n;
Step 2:利用Anscombe变换将X射线图像中泊松噪声转化为高斯噪声;
Step 3:将经过Anscombe变换后的二维图像转换为一维数组,得到n个观测变量;
Step 4:对观测到的混合信号进行中心化处理,即去均值处理[17];
Step 5:取t=0,生成随机初始矩阵为W(0);
Step 6:按照非线性递归最小二乘规则迭代;
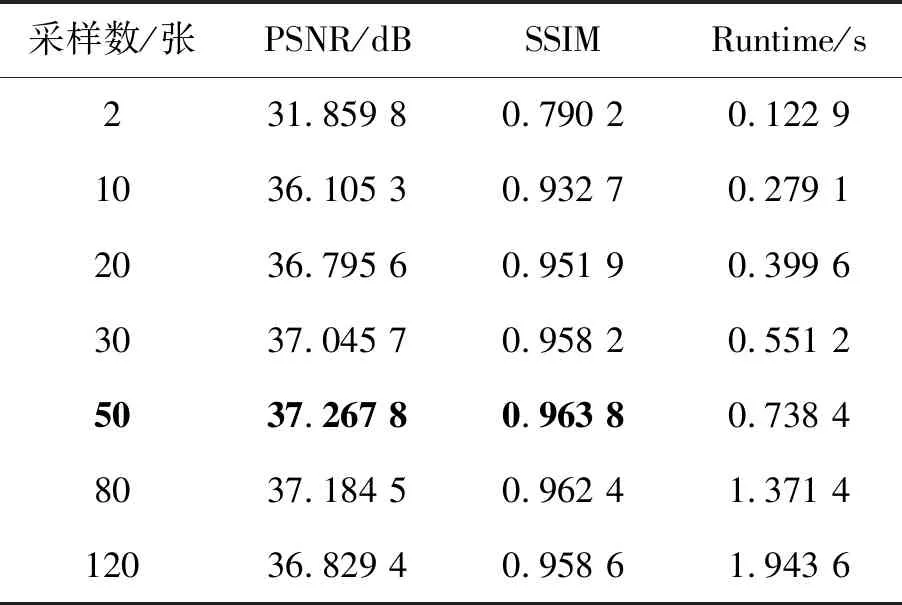
Step 7:叠加次数t=t+1,判断此次是否满足|J(W(t))-J(W(t-1))| Step 8:将分离得到的图像信号再通过Anscombe逆变换,得到最终降噪图像。 本文分别通过Shepp-Logan头模型图像和自制X射线机拍摄的图像对本文降噪算法进行性能分析。采用Shepp-Logan头模型图像是因为由它可以随机生成任意张数、任意噪声强度的含噪声图像,这有利于对本文降噪算法的降噪局限进行分析;采用真实低质量X射线图像来分析降噪方法可以验证算法的实用性。本文降噪算法的计算平台为Intel(R) Core(TM)i7-6700 CPU、@3.40 GHz 3.40 GHz四核处理器、8 GB内存的PC机。 如图2(a),Sheep-Logan头模型被用来表示一个脑部断层图像,它由10个位置大小、方向、密度各不相同的椭圆组成,通过不同的椭圆来表征不同形状,利用不同灰度值模拟不同组织的衰减系数[18]。 图2 原始图、含噪声图及降噪图 图2(a)为Sheep-Logan原始图像;图2(b)为含泊松噪声图像,其噪声是以图2(a)中像素值为均值随机生成的,其峰值信噪比(Peak Signal to Noise Ratio, PSNR)为28.289 4 dB、结构相似性(Structural Similarity Index, SSIM)为0.700 7;图2(c)~图2(i)对应采样序列中含不同图像数目时的分离降噪图像;n表示采样序列中图像数目。由图2看出:随着采样序列中图像数目的增加,降噪图像的质量得到明显改善。 表1 降噪图像性能随采样序列中图像张数的变化 Tab.1 Denoising performance varies with number of images in sequence 采样数/张PSNR/dBSSIMRuntime/s231.859 80.790 20.122 91036.105 30.932 70.279 12036.795 60.951 90.399 63037.045 70.958 20.551 25037.267 80.963 80.738 48037.184 50.962 41.371 412036.829 40.958 61.943 6 表1所示为降噪图像的PSNR、SSIM和Runtime。当采样序列中n数值从2增加到50时,降噪图像的PSNR和SSIM值明显提高,PSNR由31.859 8 dB提高到37.267 8 dB、SSIM由0.790 2提高到0.963 8。当采样序列中n数值增加到50时,本文降噪算法通过13次迭代即可以完成收敛,运行时间为0.738 4 s;继续增加采样张数,算法运行时间增加,降噪效果无明显改善。 图3 降噪图像PSNR、SSIM随序列中图像张数的变化 相应于表1的代表性数据,图3截取本文降噪算法对Sheep-Logan头模型的降噪效果随采样序列中图像张数的变化规律曲线中[2,120]段:在图像采样数目处于[2, 20]时,随着图像数目增加,降噪效果提升明显;图像采样数目处于[20, 50],图像的PSNR值以及SSIM值提升缓慢,图像采样数目为50,降噪效果最佳;图像采样数目处于[50, +∞),降噪效果无明显提升,但可以通过改变算法精度完善。 图4 不同降噪算法的降噪效果图 此外,图4给出本文降噪算法同几种常见消除泊松噪声的算法降噪效果比较。图4(a)为含噪声图像;图4(b)为软阈值小波(Wavelet)降噪图像;图4(c)为双边滤波(Bilateral filter)降噪图像;图4(d)为Anscombe+BM3D降噪图像;图4(e)为参考文献[19]的SVD+Sequence降噪图像[19],序列中图像数目为9;图4(f)为本文降噪算法的降噪图像,序列中图像数目同样取9。在视觉效果上比较:图4(b)噪声残留较多;图4(c)细节轮廓不全;图4(d)图像亮度较差;图4(e)和图4(f)在图像亮度和细节轮廓保留上有优势,且图4(f)效果最优。 表2 不同降噪算法性能对比 表2为对应图4的算法性能参数对比,对比评价参数:本文降噪算法在降噪效果上最优,且在运行时间上也具有明显优势。 在使用真实X射线图像对本文降噪算法进行性能分析时,选用实验组自制的X射线机拍摄9帧像素为768×576的X射线图像组成图像序列。由于无“干净”原图像做降噪对比,这里采用信噪比(Signal Noise Ratio,SNR)、信息熵(Entropy)、标准差(Standard Deviation, SD)和运行时间(Runtime)作评价参数,与参考文献[19]的SVD+Sequence降噪方法做对比。 图5 两种算法在不同采样图像数目下的降噪效果对比 图5中,图5(a)为采用本文降噪算法的降噪效果及其边缘检测图,图5(b)为采用SVD+Sequence降噪算法的降噪效果及相应边缘检测图。 图6 SNR,SD,Entropy和Runtime上的对比 图6给出了本文降噪算法和参考文献[19]降噪算法的对比曲线,横坐标均为序列中采样图像数目。图6(a)为SNR对比,由此可见当序列中图像数目由2增加到9时,本文降噪算法的SNR值由30.355 1 dB提高到65.949 8 dB,高于SVD+Sequence算法的SNR值;图6(b)为SD对比,可见本文降噪算法的降噪图像SD较低,说明其受像素值干扰较小;图6(c)为Entropy对比,可见当序列中图像数目由2增加到9时,本文降噪算法图像Entropy从5.923 5提高到6.022 3,值优于SVD+Sequence算法,说明本文降噪算法更有效保留细节信息;图6(d)为Runtime对比,可见本文降噪算法运行时间较长,采用9张X射线图像降噪时,迭代16次,Runtime为1.311 s,同样满足实时观测需要。 由图5和图6得出结论:当参与降噪的图像张数增加时,两种算法的降噪效果均有改善且图像边缘更完整;本文降噪算法在降噪效果及边缘细节保留上更优;本文降噪算法在运算时间上不占优势。 图7 其他常用降噪算法的降噪效果图 图7给出本文降噪算法同其他几种常用降噪算法的降噪效果对比,这里采样序列中图像数目为9。图7(a),7(d)分别为Wavelet降噪图及对应边缘检测图;图7(b),7(e)为Bilateral filter降噪图及对应边缘检测图;图7(c),7(f)为Anscombe+BM3D降噪图及对应边缘检测图。由对比看出,相比较图5(a)中本文降噪算法(n=9),常见的这3种算法得到的降噪图像中噪声残留更多,图像细节、边缘保留较差。这说明:当序列中取适当数量含噪声图像时,本文降噪算法更具性能优势,不仅可以有效分离噪声,还可以有效保留图像的轮廓边缘和细节信息。 表3为图7所示图像的SNR,Entropy,SD以及Runtime。图像SNR值高说明算法对于噪声滤除更有效;Entropy高则说明降噪后图像中细节信息保存较多;图像SD大说明像素值受干扰较大。分析数据说明:本文降噪算法在降噪和信息保留上均优于其他算法,同时算法运行时间也满足实时需要。 表3 常用降噪算法降噪性能对比 Tab.3 Denoising performance comparison of common algorithms 降噪算法SNR/dBEntropySDRuntime/sWavelet55.304 45.959 870.7960.299Bilateral filter47.274 35.903 470.8151.625Anscombe+BM3D51.377 55.962 571.0354.596SVD+Sequence[19]47.233 75.863 670.8340.381Proposed denoising65.94986.022 370.7821.311 本研究介绍一种基于Anscombe变换的X射线图像序列盲源分离降噪方法,并分别利用Sheep-Logan模型图像和真实X射线图像对该降噪方法的性能进行评价分析。分析结果表明:随着图像序列中采样张数增加,本文算法降噪效果显著提高,并在采样张数达到50的时候,降噪性能达到最优;增加图像序列中采样张数会提高降噪性能,但也会增加算法运行时间,需要根据实际情况找到运行时间和降噪性能的平衡;本文降噪算法性能可以通过GPU得以大大改善,是一种实用的降噪方法。3 本文降噪算法性能分析
3.1 采用Sheep-Logan头模图像对本文降噪算法进行性能分析




3.2 真实X射线图像对本文降噪算法的性能分析


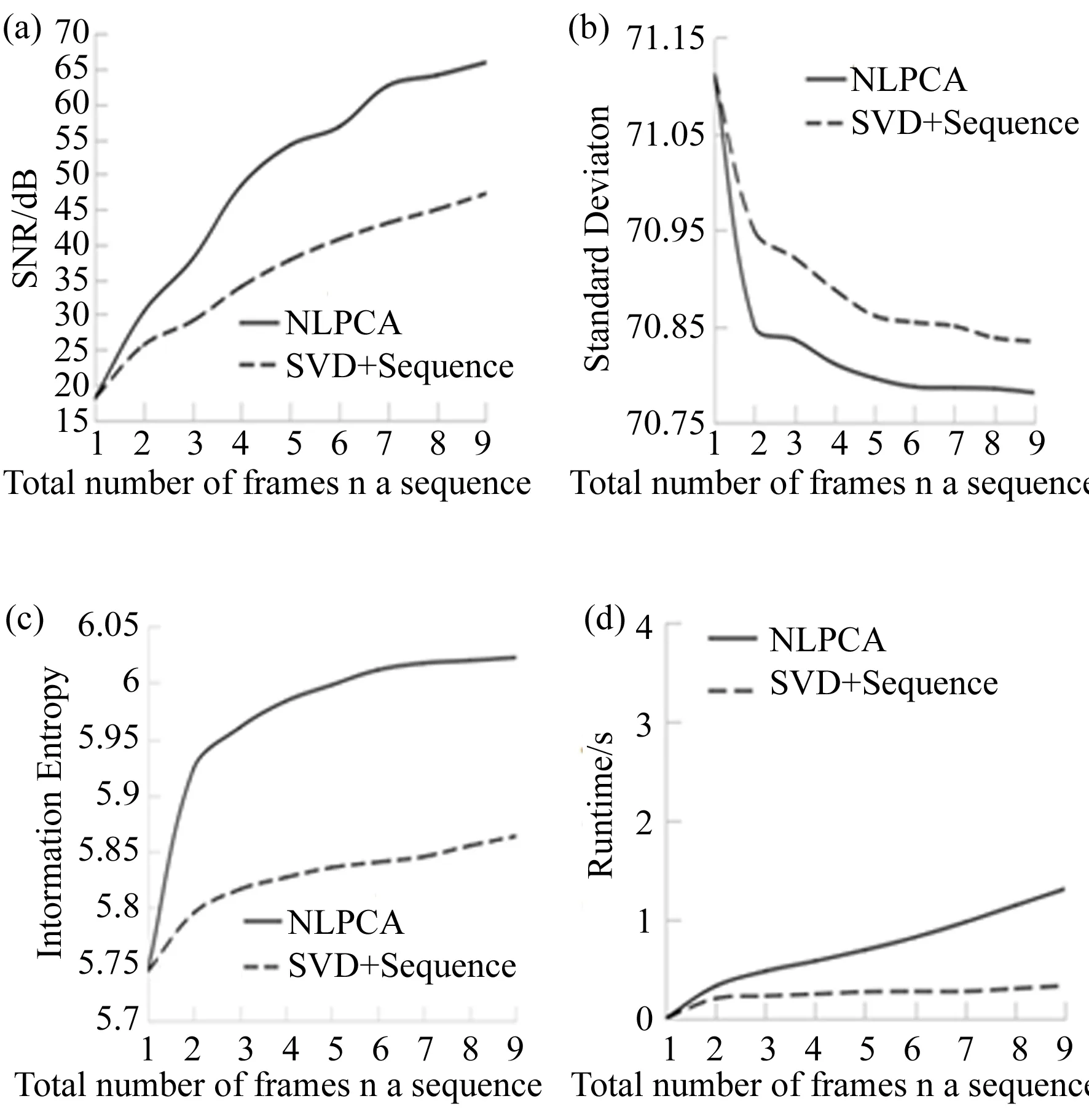


4 结 论

