基于深度相机的大场景三维重建

刘东生，陈建林，费 点，张之江

(上海大学 特种光纤与光接入网重点实验室，上海 200444)

1 引 言

大型场景的三维重建是图形学和计算机视觉领域的一个研究热点，被广泛应用于室内设计、机器人导航和增强现实。在表面重建系统中，需要同时精确地获取相机的运动轨迹和场景的三维模型。深度相机因其能以视频帧速直接获取物体的位置信息且价格低廉，而非常适合用来研究三维重建。

KinectFusion[1]系统开创了使用手持式深度传感器进行实时稠密重建的新领域。它采用点到平面的迭代最近点算法(Iterative Closest Point,ICP[2])将输入的深度图与当前模型配准来跟踪相机，实时性能由GPU的并行计算来实现。然而KinectFusion只能重建固定于空间中的小场景，并且相机位姿估计不精确。随后，研究者使用移动网格的策略来扩展KinectFusion算法，使其能重建大型场景[3-5]。但对于大型场景重建，长的相机扫描序列会引入越来越大的位姿累积误差，测量的表面信息被不精确地融合到模型中，会进一步恶化位姿估计的结果，最终导致相机漂移，重建的模型质量差，甚至是重建失败。

为了解决上述问题，Fioraio等人[5]使用最新K张深度图像构建局部子网格，以帧到模型的方式执行相机跟踪。尽管该方法可极大地减少累积误差，但当场景缺少几何结构特征时，仅利用深度信息进行重建会使相机丢失跟踪。Fu等人[6]在跟踪相机的同时检测场景闭环，以闭环为约束来矫正相机轨迹。但检测的闭环存在错误且有部分正确的闭环并未被检测。Choi等人的离线方法[7-8]采用基于线流程(Line processes)的鲁棒全局位姿优化来消除检测错误的闭环以提高重建质量，但需耗费大量时间。在Dai等人[9]的BundleFusion算法中，新输入的RGB-D图像需要和之前所有分块的关键帧匹配，以高斯牛顿法的求解方式极小化位姿对齐误差来优化全局轨迹，可得到精确的相机位姿，但需要两张显卡执行复杂的局部和全局优化。

针对大场景重建中，由位姿估计的累积误差而导致的相机漂移、重建模型质量低的问题，本文设计了一种基于深度相机的场景重建方法。在系统中保持一个K长的滑动窗口，基于由最新K帧融合的彩色模型跟踪相机，以此来减少局部累积误差。在全局优化中，迭代步长式地在子网格间搜索表面对应点，并以对应点的点到平面距离误差和亮度误差为约束，优化全局相机轨迹。最后通过实验证明了本文方法的有效性。

2 三维重建流程

基于深度相机的静态场景重建方法都有相似的系统框架，如图1(a)所示。

首先，对输入的RGB-D图像执行深度图像预处理以减少噪声和错误的深度值。其次，取决于不同的方法，从预处理过的深度图像中获取不同类型的深度信息。随后，可利用帧到帧、帧到模型的方式计算当前图像到全局坐标系的最优变换。最后，将当前深度图的所有顶点转换到全局坐标系并融合到模型中。

为了重建大型场景，本文方法的流程如图1(b)所示。随着深度相机在静态场景中扫描，根据时间戳对齐一对深度和彩色图像。在算法启动时，将第一个子网格固定于相机正前方，子网格内的体素由第一对深度和彩色图像初始化，用于后续的相机跟踪。

在每个子网格内，结合彩色和深度测量执行帧到模型的相机跟踪。考虑到短时间内的累积误差小，且物体的颜色亮度可能在不同视角下有些许变化，本文提出使用彩色模型的去融合方案来减少累积误差。核心思想是当第N对图像融合到模型时，将N-K对图像从模型中去融合，以此来确保输入的图像始终基于最新的K对帧估计位姿。

当相机相对于当前子网格中心点的位置超过给定阈值时，为了高效性，将子网格平移体素单元倍数的距离。移动到子网格外面的体素会丢失，而剩余的体素会从旧的子网格复制到新的子网格以继续执行帧到模型的相机跟踪。

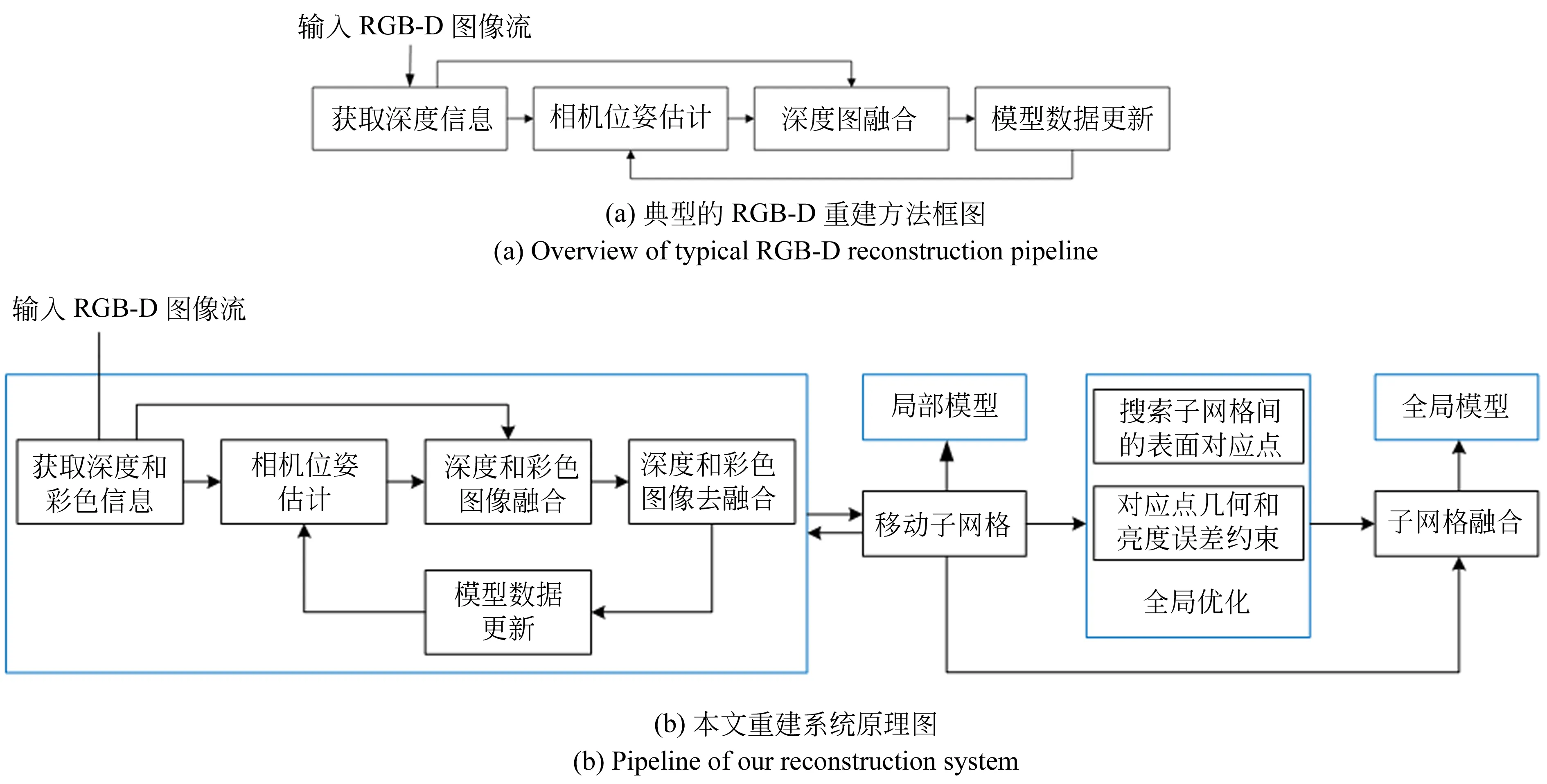
图1 三维重建流程

在全局优化中，本文提出了迭代步长式的方法在子网格间搜索对应表面点，并基于对应点的点到平面距离约束和亮度约束迭代地执行全局优化，目标函以sparseLM的方式求解。相机轨迹优化后，将子网格全局配准，融合到全局网格中[10]。随后，采用marching cubes[11]算法提取三角片面以便可视化。

3 场景重建的算法

3.1 相机模型及符号表示

对于一个三维空间点P(x,y,z)∈3，可以使用针孔相机模型获取其对应于二维图像平面的像素点X(u,v)∈2

(u,v)T=π(x,y,z)=

(1)

其中fx,fy和cx,cy分别是焦距和光轴中心点坐标，π为投影方程。

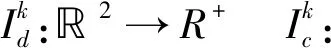
(2)

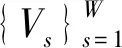
(3)

其中:三维正交矩阵Rl,k∈3×3表示旋转分量，tl,k∈3×1表示平移分量。

3.2 鲁棒的相机跟踪及数据融合

本文采用文献[12]的方法估计相机位姿。如图2所示，使用加权截断有向距离函数(TSDF[10])表示三维空间:

ψ:[ψrgb,ψd]→[3,],

(4)

其中ψrgb与ψd分别表示重建表面的色彩和几何信息。

给定由前N对深度和彩色图像融合的表面ψf_n，和由第N+1对深度和彩色图像的反投影得到的表面ψs_n+1，其几何位置和颜色亮度应尽可能一致。误差函数可定义为：

E(Tl,N+1)=

(5)

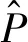
(6)

点P定义于第N+1帧的相机坐标系，Ω为一个三维对角矩阵，将RGB格式的彩色图转换为灰度图[13]:

(7)

误差函数(5)可使用Gauss-Newton算法迭代求解直至收敛。

图2 表面ψs_n+1与ψf_n的几何位置和颜色亮度应尽可能一致

本文在每个体素v中分配6个值，其中Φ是从v到最近表面的TSDF，R,G,B是三通道颜色值，Wd和Wc分别为TSDF和颜色值的确信度。在估计完第N+1对图像的位姿后，可使用加权平均法[10]更新TSDF:

(8)

类似地，以相同的方式更新颜色信息:

γ∈{r,g,b}.

(9)

3.3 基于深度和彩色信息的去融合

针对位姿估计存在累积误差的问题，本文在文献[5]的基础上，结合深度和彩色信息对模型去融合。

考虑到短时间内累积误差可忽略不计，本文基于由最新的K帧深度和彩色图像融合的模型跟踪相机。在当前帧融合到模型后，将N-K帧的信息从模型中去融合，在程序中该过程对应于一个K长的FIFO队列，如图3所示，直到第N-1+C帧时生成一个新的子体积。去融合过程可表示为:

(10)

(11)

图3 子网格的融合和去融合

对于彩色测量的累积误差，以同样的方式:

γ∈{r,g,b}.

(12)

若小于K帧图像被跟踪，则不对子网格去融合。一旦超过K帧被处理且满足子网格的移动条件，则将当前子网格保存在内存中。

3.4 子网格的移动策略

当相机的位置距离子网格的中心点超过给定阈值时，需要移动子网格来重建大型场景。

如图4所示(彩图见期刊电子版)，相机从路标L1移动到路标L2。橙色线表示相机光轴，相机在L1处采集到第1帧图像，其位姿为I4×4，并新建子网格V1，中心点为O1，如绿色实线框所示。在任意时刻t, 第i帧图像和当前子网格Vj的绝对位姿可分别表示为Tg,i和Pg,j，Tj,i为第i帧到局部子网格Vj的变换:

(13)

在移动子网格时，如果同时考虑平移和旋转分量，则当下列条件满足时:

‖tji‖>Thold_t或aji=

‖rodrigues-1(Rj,i)‖>Thold_R,

(14)

Vj被移动到Vj+1，如图4中的蓝色虚线框所示。其中Thold_t和Thold_R分别为距离和角度阈值，rodrigues为罗德里格斯变换。此时，对于新建立的子网格Vj+1，有:

Tj+1,i=I4×4,Pj,j+1=Tj,iTj+1,i-1=Tj,i,

(15)

Vj中的体素需要被三线性插值到Vj+1中，会耗费大量时间。同时，由于体素在三线性插值后通常位于非整数坐标处，因此插值方法会影响重建的准确性。

本文采用图4所示的子网格移动方法，其中黑色实线箭头表示O1与L2处光轴的距离，交光轴于点C。当该距离超过给定阈值dth_1时，移动V1:

d1>dth_1.

(16)

考虑到三线性插值非常耗时且会引入不精确的tsdf， 本文将V1平移体素单元倍数的距离。同时，为了使平移到新建的子网格内用于相机跟踪的有效体素数量尽可能的多，点O1被平移到蓝色虚线框的中心点O2，生成一个新的子网格，如图4红色虚线框所示。此时，L2处满足子网格移动条件的相机视角在新的子网格内具有很大的覆盖范围，如图4黄色箭头所示。因此，随后用于相机跟踪的实体素数量众多，相机跟踪会更加精确鲁棒。V1被平移整数体素单元的距离，最终生成的子网格如红色实线框所示，此时子网格之间的位姿有以下关系:

Pj,j+1=

(17)

vs为单个体素的尺寸。

需要注意的是，当相机沿着固定光轴向前或向后移动超过一定距离时，V1同样需要被平移:

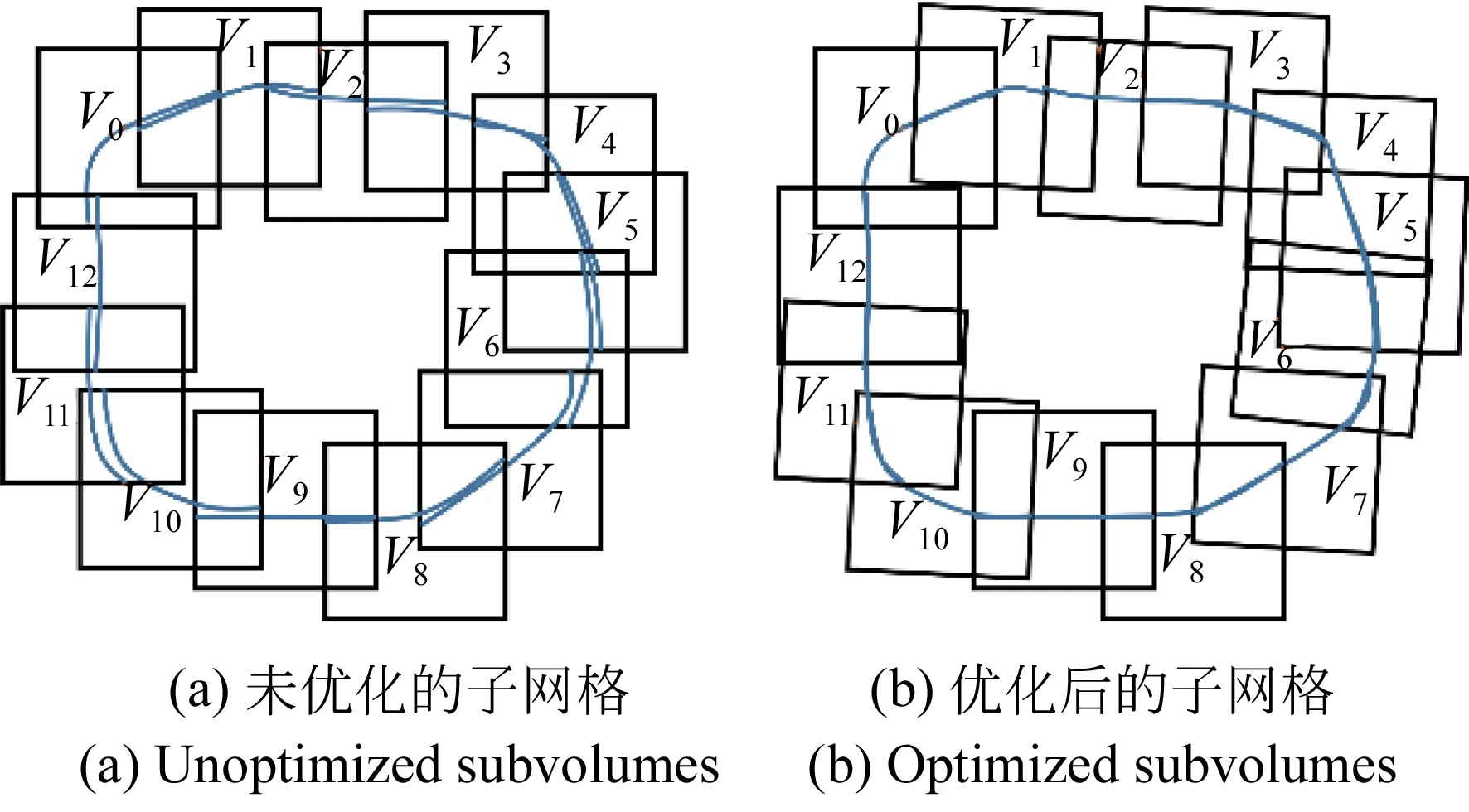
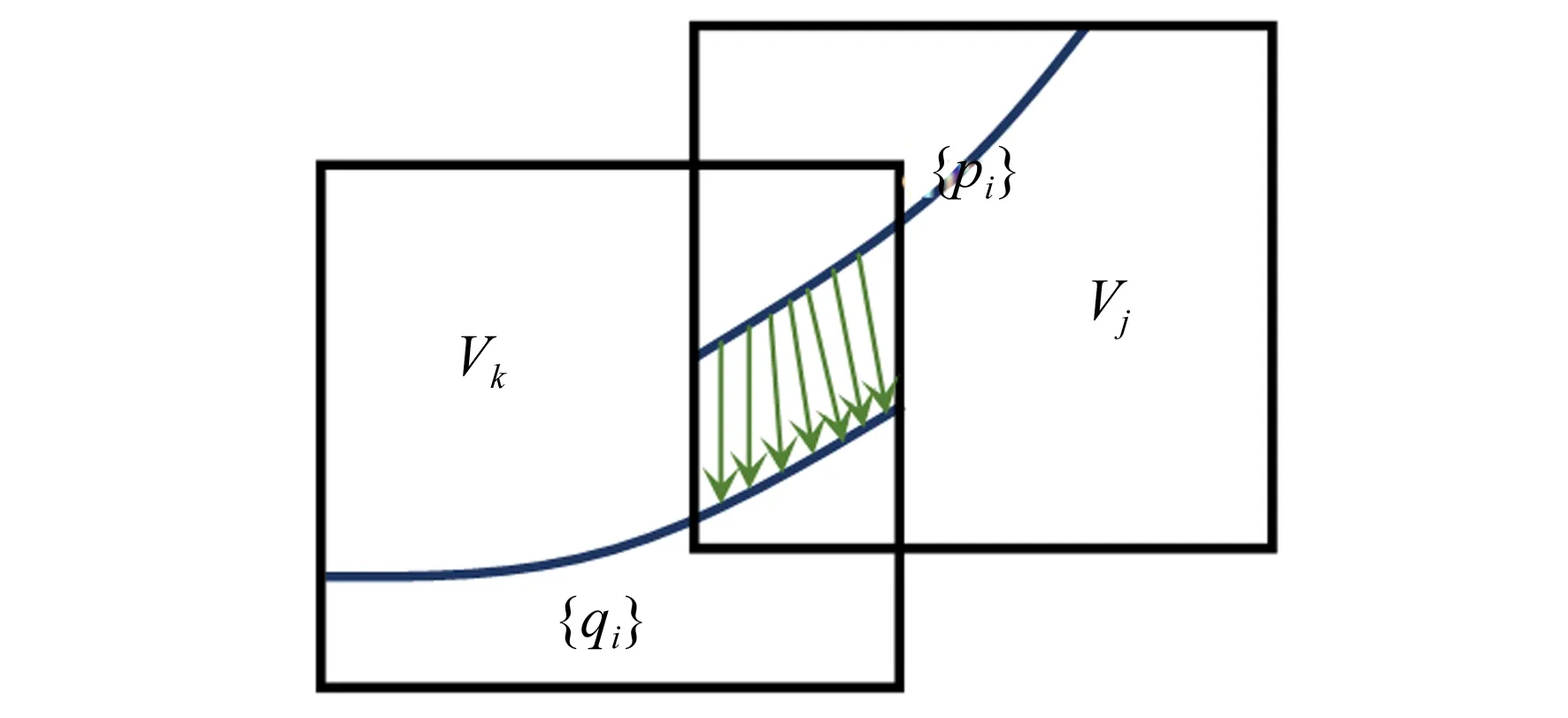
d2>dth_2_l‖d2

(18)

其中d2是点C到光心L2的距离，dth_2_l和dth_2_s为两个阈值。当式(17)或式(18)满足时，平移V1。移动到子网格外的体素将会丢失，剩余的体素将从旧的子网格复制到新的子网格。

图4 将子网格从L1平移到L2

3.5 全局优化

虽然相机在每个子网格内是低漂移的，但由于长的扫描序列，子网格之间不可避免地存在累积误差。本文基于文献[5]的全局优化框架，提出了迭代步长式地寻找表面对应点。如图5(a)是未优化的子网格，图5(b)是优化后的子网格。

图5 全局优化的示意图

3.5.1 迭代步长式寻找表面对应点

如图6，P={pi}和Q={qi}是子网格Vj和Vk的表面点集，pi和qi是一对对应点，Tg,j和Tg,k为子网格Vj和Vk的全局变换。若Tg,j和Tg,k都被精确地估计，则可建立以下方程:

(19)

为了表述简洁，公式中默认存在点的齐次形式与非齐次形式间的转换。

通常，由于噪声的存在，式(19)不会相等。为了得到Tg,j和Tg,k的精确值，需要在Vj和Vk中寻找更加精确的对应点。

对于任意表面点P，假设其tsdf值为ψd,可获取归一化的梯度:

(20)

因tsdf表示一点距表面的有向距离，故Vk中的对应点可通过以下方式搜索:

(21)

在式(21)中，Vj中的表面点pi被转换到Vk中，并沿着转换后的点的法线方向行进αψd的距离。理论上仅仅需要行进距离ψd，但在实验中发现，由于位姿估计和tsdf计算过程中存在误差，寻找到的对应点不一定是Vk的表面点。因此，本文引入步长参数α，基于实验经验，α由0.8增长到1.2，增量为Δα= 0.05，直到找到tsdf值足够小的点qi。如果α增长到1.2之后，qi仍然远离表面，则认为pi没有对应点。

图6 Vj和Vk之间寻找对应点

3.5.2 迭代式的全局优化

对于一对对应点(pi,qi)，其三维空间位置和亮度应尽可能地一致。误差函数可表示为:

ei,i=‖(Tg,jpi-Tg,kqi)TTg,kn‖+

(22)

对于寻找的对应点集，整体误差函数可定义为如式(23)，可使用sparseLM求解：

E(Tg)=

(23)

在本文中，设置迭代次数Nth，如果相邻两次迭代的优化误差小于给定阈值或者迭代次数超过Nth时，则停止迭代，输出优化后的相机位姿。

3.5.3 获取全局一致的三维模型

在全局轨迹优化后，为了得到整体的三维模型，需将子网格融合到全局TSDF中:

(24)

类似地，对于彩色信息:

(25)

随后使用marching cubes[11]算法提取三角片面以获得精细的三维场景模型。

4 实验结果及分析

本节使用两类不同的数据分别从定性和定量两个方面验证本文算法的有效性。

4.1 场景重建结果的定性展示

图7是由Kinect v2从实验室中采集的450张深度和彩色图像重建的模型。图7(a)和图7(b)分别从两个不同的视角展示了重建的结果。可以看出，尽管场景中的物体繁杂多样，但最终重建的结果清晰地展示了实验室内部的结构。图7(c)展示了书桌部分的局部细节图，可以看到书桌、显示器屏幕、纸箱表面都平坦光滑，甚至纸箱表面上贴的透明胶带都清晰可见。图7(d)展示了书架部分的局部细节图，垃圾桶、植物、书架上摆放的书本、玩偶都实现了较高水平的还原。

图7 实验室的重建结果

此外，本文还重建了Augmented_ICL_NUIM[5]数据集中的客厅(Living Room2)部分场景，并与现有方法进行了比较，验证了本文提出算法的有效性。

图8分别展示了4种方法的重建结果。图8(a)为Bylow等人[14]的重建模型，与 KinectFusion[1]中通过点到平面的ICP 算法跟踪相机不同，Bylow 等人直接基于TSDF最小化深度测量误差，有效地提高了位姿估计的精确度。但仅通过单一网格持续估计位姿并融合数据，位姿误差不断累积，不准确的位姿导致融合的模型出现模糊或者断裂现象，如8(a)中台灯的灯柱和植物的枝叶所示。图8(b)为Fioraio等人[5]的重建结果，为了减少累积误差，Fioraio等人沿着相机运动轨迹新建子网格，子网格内局部场景的细节精细度有所提升，模型中台灯的灯柱和植物等细节都基本保留。但其在全局优化中寻找的对应点不够精确，导致子网格之间的相对位姿仍然存在较大误差，重建模型中的墙壁、沙发等处存在明显的折痕。图8(c)为Choi等人[8]的重建结果，该算法间隔固定帧数(实验中为50帧)生成一个新的子网格，但当相机运动速度较快时，单个子网格内覆盖的场景较大，包含的相机运动轨迹较长，重建模型细节处容易出现空洞，如模型中的靠枕和植物所示。图8(d)为本文提出方法的重建结果，本文结合深度和彩色测量跟踪相机位姿，同时对深度和彩色数据进行融合和去融合操作，估计的位姿更加准确，并且子网格间采用更加精确的步长式方法寻找对应点，极大程度地减轻了折痕现象，同时保证了子网格内局部场景的细节精细度，如图中的靠枕和植物。

图8 四种方法的重建结果对比

通过自采数据和公开数据集的实验结果分析，本文提出的场景重建方法能够克服较长相机轨迹带来的累积误差问题，重建的模型平滑且完整，同时保留了精致的局部细节，最终生成的三维模型具有更佳的可观性。

4.2 绝对轨迹误差的定量分析

表1所示为四种方法对数据集Augmented ICL-NUIM Living Room2部分场景评估的绝对轨迹误差(ATE)，其中包括均方根误差(RMSE)、平均值(Mean)和标准差(STD)，单位均为米。从表中可看出，相较于现有的几种方法，本文方法估计的绝对轨迹误差最低，均方根误差 RMSE 与 Choi等人提出的算法相比低 14.1%，说明本文提出的算法在位姿估计准确率上得到了很大提升。

表1 四种不同方法估计的相机绝对轨迹误差

Tab.1 Absolute trajectory error evaluated by four different methods

(m)

4.3 重建时间的定量分析

表2所示为三种方法对自采的450张实验室场景数据集评估的重建时间。需要说明的是，本文基于Fioraio[5]等人的方法实现整体模型配准，融合效率已在文献[5]中说明。与文献[5]不同的是，此处的对比实验基于串行CPU，硬件环境为i5-7300HQ、2.5 GHz英特尔CPU。

相比Bylow[14]等人直接配准单张深度图像，Fioraio[5]等人需对深度图像去融合，且需新建子网格，后续还需对子网格融合配准。而本文在文献[5]的基础上加上了彩色图像的配准和去融合，且在子网格间迭代式地寻找对应点，使用迭代式地方式优化全局误差函数，因此耗费时间比文献[14]，文献[5]都长。

表2 三种不同方法的重建时间对比

Tab.2 Reconstruction time for four different methods

方法Bylow[14]Fioraio[5]本文总体重建耗时/s99170190平均每帧耗时/ms221378423

后续使用GPU实现代码加速可极大地减少重建时间，理论上可达到Fioraio[5]等人的重建效率。

4.4 实验中的参数分析

除了上述定性和定量的实验，本节还研究了算法中相关参数对重建效果的影响，包括位姿跟踪中用于调节彩色误差在总误差中所占比例的权重参数θ和迭代步长参数α。实验均基于Augmented ICL-NUIM Living Room2数据集。

表3 不同权重θ对绝对轨迹误差的影响

表3所示为不同θ值对相机运动轨迹误差的影响。当θ=0，此时彩色误差占比为 0，位姿跟踪中仅使用了深度数据；当θ=100，此时彩色误差占比为92%，位姿跟踪中彩色信息起决定性的作用。当θ=8时，彩色误差和深度误差共同作用于位姿跟踪，RMSE最小。

此外，对于全局优化，本文还设置了三组对比实验，分别命名为A：未优化的绝对轨迹RMSE。B：迭代步长α=1.0，优化后的绝对轨迹RMSE。C：本文迭代步长式寻找对应点，优化后的绝对轨迹RMSE。表4展示了实验结果。从表中可看出，迭代步长式寻找对应点方法比直接寻找对应点方法轨迹优化结果提升8%。

表4 迭代步长α对绝对轨迹误差的影响

由上述实验结果可知，本文提出的三维重建方法可减少位姿估计中的累积误差，得到的相机轨迹更加精确。

5 结 论

针对大场景重建中，相机位姿估计的累积误差导致相机漂移、重建模型质量低的问题，提出了基于深度相机的高质量三维场景重建方案。针对在缺少几何结构特征的场景中，仅使用深度信息跟踪相机易于失败的问题，结合深度和彩色测量以帧到模型的方式跟踪相机；针对位姿估计中存在累积误差，提出结合深度和彩色信息的去融合方案；在全局轨迹优化中提出迭代步长式地寻找表面对应点，并以对应点的欧氏距离和亮度信息为约束，优化全局相机位姿。

本文在传统的三维重建框架基础上提出了彩色信息去融合方案，并在全局优化中引入迭代步长，提高了相机轨迹的精确度。与基于深度相机的重建方法对比，本文提出的重建方法相机轨迹精度提升14.1%，基于实际数据实验，本文方法能实现精确的相机跟踪，重建高质量的场景模型。满足实际应用需求。本文的算法基于串行CPU实现，重建时间相对较长。同时本文使用归一化体素网格表示三维场景，内存消耗大，因此限制了重建的场景大小。后续工作可将算法移植到CUDA平台，用于GPU加速。同时使用Octree[19]或Voxel Hashing[20]来表示重建空间，以便重建更大场景。