大型光学系统波前检测中气流扰动的抑制

徐抒岩，张旭升，范 阔，鞠国浩

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

随着人们对遥感与天文领域光学成像分辨率与观测视场要求的不断提高，大口径、长焦距、多反射镜光学系统已成为当前成像光学仪器的主要发展方向[1]。光学装调精度是影响系统最终成像质量的主要因素之一[2]。然而，大口径、多反射镜系统装调公差要求严格，需要确定的镜面位置自由度数量较多，导致其装调难度很大。系统波前测量精度在很大程度上决定了系统装调精度。系统装调过程需要利用多个视场波前测量数据准确计算各镜面失调量，在此基础上再进行相应的位姿调整，最终完成装调[3-5]。所以，波前像差的准确测量是实现高精度系统装调的必要条件。

然而，大口径、长焦距光学系统的波前测量精度易受气流扰动的影响。一方面，口径大使得自准直检测光路横截面内温度分布的非均匀性较高；另一方面，焦距长意味着自准直干涉光路光程较长，由温度非均匀性引起的空气折射率非均匀性对总光程影响较大。所以，高精度波前检测中，气流扰动是必须要考虑的误差因素。实验室内热源(干涉仪、工控机以及装调人员等)与热沉(大地与金属气浮平台、调整架等)使得气流扰动一直存在，这将导致自准直回路内温度分布的非均匀性与动态性，持续对波前检测精度造成影响。理想条件下，可将光学系统置于真空罐内进行装调。然而，大型真空罐的使用费用高昂，会增加整个光学仪器的研制费用与研制周期。所以，需要研究抑制气流扰动影响的方法，以提高非真空条件下系统的波前测量精度。

近年来，针对光学检测过程中气流扰动影响的研究已有很多[6-10]。2009年，中科院成都光电所以有限元分析法为基础将空气扰动等效为多个界面的扰动，并将温度不均匀的空气视为由不同折射率薄透镜组成的光学系统，对空气温度变化的影响进行建模仿真，这对于分析气流扰动问题具有一定的指导意义[6]。2011年，中科院长春光机所针对镜面面形检测过程中外界条件对(参考面和测试面之间)光腔折射率的影响建立流体仿真模型，分析了不同气流状态下光腔温度、压强分布情况及它们对波前像差的影响；另外，还分析了通过提高送风速度来减小光腔温度分布不均匀性及提高镜面面形检测精度的可行性[7]。2015年，中科院南京天文与光学技术研究所分析了不同曲率半径球面反射镜在水平和垂直两种检测情形下，垂直方向温度梯度对面形检测精度的影响，结果表明，温度梯度对水平检验光路的影响远大于垂直检测光路[8]。另外，中科院成都光电所运用温度场理论对实心镜面主镜视宁度及“气刀”的改善效果进行了详细的研究，提出了一种灵活多变、可操作性强的蜂窝镜面温度控制方案，这对于抑制由气流紊乱引起的主镜视宁度问题具有一定指导意义[9]。

综上可知，通过主动送风手段控制室内温度场，可以抑制气流扰动对光学检测精度的影响，然而，上述研究大都基于仿真模拟，没有根据实际大口径、长焦距光学系统具体检测环境提出相应的温度场控制方法，并进行相关实验验证。即便部分文献含有相关实验验证[7]，其实验系统结构相对简单，口径较小，且构成的自准直干涉光路光程较短。实际上，这一类系统波前检测过程受气流扰动的影响较小，并不适合分析气流扰动的影响。所以，相关实验结论对于解决实际大口径、长焦距、多镜面光学系统波前检测过程中气流扰动抑制问题的参考价值较低。

本文针对口径为500 mm、焦距为6 000 mm的离轴三反望远镜实际检测光路及实验室环境条件，以计算流体力学为理论基础，通过仿真建模提出一种利用风扇阵列主动送风的室内温度场控制方法，并进行与之对应的实验验证。通过比较温度场控制前后多组实际像差系数测量数据(每组包含约250单次测量数据)的标准差，充分验证本文所提出方法的有效性。本文对于抑制大口径、长焦距、多镜面光学系统波前检测过程中气流扰动的影响具有一定参考价值，对于提高该类型光学系统的装调精度与装调效率具有重要意义。

2 气流扰动抑制机理

2.1 气流扰动影响波前检测精度的原因分析

本节首先说明空气折射率与温度之间的关系[11-12]，采用Birch等所提出的公式来描述不同环境条件下空气的折射率。首先，温度为15 ℃、压强为101.325 kPa 、CO2体积混合比为4.5×10-3的干空气的折射率ns为(适用波长为0.2～2.0 μm)：

(1)

式中：λ为光波长，A,B,C为特定常数。然后可得任意温度和压强下(CO2体积混合比为4.5×10-3)干空气的折射率ntp为：

(2)

式中：p为空气压强，t为空气温度，D～G为特定常数。在公式(2)的基础上，可继续写出不同湿度下空气的折射率(本文不再赘述)。

从公式(2)中可以看出，空气折射率与温度密切相关。而实际光学检测过程中，空气温度不均匀且处于动态变化中，导致检测光路内空气折射率不均匀且动态变化，从而引入波前测量误差。

首先，实验室内热源(干涉仪、工控机以及装调人员等)与热沉(大地、金属气浮平台以及调整架等)的存在使得室内存在一个不均匀的温度场，造成室内空气折射率的非均匀性。即使通过一定手段将工控机等热源移出实验室(实验室外远程控制)，大地以及金属气浮台等热沉却一直存在，依然会造成实验室内的非均匀温度场，引入波前测量误差。

其次，空气具有热惯性小、易流动性的特点，任何的轻微扰动都会引起空气的运动，同时伴随着热量的传输，这导致实际中室内温度场一直处于动态变化中。可通过长时间的稳定来降低温度场的动态性，然而这会大大降低波前检测的效率。实验室与外界热交换无法隔绝，室内温度场难以达到理想的“稳态”，此时干涉光路内空气温度依然会存在一定的“慢漂”，影响波前检测精度。

2.2 通过主动送风抑制气流扰动影响的机理分析

室内温度的非均匀性可通过主动送风(或称强制对流)进行改善。本节基于计算流体动力学理论对此进行定性说明。在流体动力学计算中包含3个基本方程式，即：连续性方程式、动量方程式和能量方程式，分别对应于物质的质量守恒定律、动量守恒定律和能量守恒定律[13-14]。

2.2.1 连续性方程

由于流体为连续介质，在研究流体运动时，认为此过程中流体充满它所占据的空间。根据质量守恒定律，对于任意空间固定的封闭曲面，流入与流出的流体质量之差应为封闭曲面内质量的变化量，公式描述如下：

(3)

式中：ρ为材料密度，vx，vy，vz为三个方向的速度矢量。

2.2.2 动量方程

该方程表述作用在各质点上的力之和与其动量之间的关系，又称为N-S方程。该方程表述为微元体内，流体的动量对时间的变化率等于作用在微元上的外力之和：

(4)

式中：P为压力，η为黏性系数，J为电流密度，B为电磁场密度。方程右边四项依次为压力梯度、黏性力、电磁力和重力。该方程能够比较准确地描述实际流体的流动。实际中往往利用数值方法求解此方程。

2.2.3 能量方程

能量守恒是包含有热量交换的流动系统必须满足的基本定律。该定律可表述为微元体内能量的增加率等于进入微元体的静热流量加上体积力和面力对微元体做的功：

(5)

式中：Cp为定压比热容，K为导热系数。公式右边四项依次为传导的热量、对流辐射热量、电阻热和化学热。

根据动量方程可知，主动送风过程首先会引起一部分空气的快速运动；再由连续性方程可知，主动送风将会引起室内整个空气流场的循环运动；最后，根据能量方程，温度不同的气流相互融合并进行热量传递，最终能够在一定程度上提高室内温度的均匀性，也就相应地提高了折射率的均匀性，降低了气流扰动对光学检测结果的影响。通过主动送风可扰乱自准直干涉光路所处的空气温度场，使得气流扰动对像差系数精度的影响成为一种高斯分布形式的随机误差；在此基础上，再通过多次取平均的手段降低测量数据的不确定度，最终得到较高的测量精度。

3 基于主动送风的温度场控制

本节针对口径为500 mm、焦距为6 000 mm的离轴三反望远镜检测光路以及实际环境条件，利用建模仿真手段，提出合理的(基于主动送风的)温度场控制方案。离轴三反望远镜的相关系统参数如表1所示。

表1 离轴三反望远镜系统参数

Tab.1 Optical parameters of off-axis TMA telescope

参数值口径/mm500光瞳离轴量/mm-460波长/nm632.8焦距/mm6 000视场/(°)1.1×0.25偏视场/(°)-0.3

离轴三反望远镜的自准直干涉光路示意图如图1所示。离轴三反望远镜、干涉仪以及平面反射镜置于气浮平台之上。再考虑实际室内测量环境的空间大小以及所具有的相关装置(比如调整干涉仪所需的大型调整架)，室内空气流场的计算流域以及坐标系定义如图2所示。由于光学系统下方(温度较低的)气浮平台与光学系统上方(温度较高的)空气产生的温度梯度主要沿竖直方向，本文选择的主动送风方式为水平送风(与温度梯度方向垂直)。与该送风方式相对应的风扇阵列位置已在图2中标出。

图1 自准直干涉光路示意图

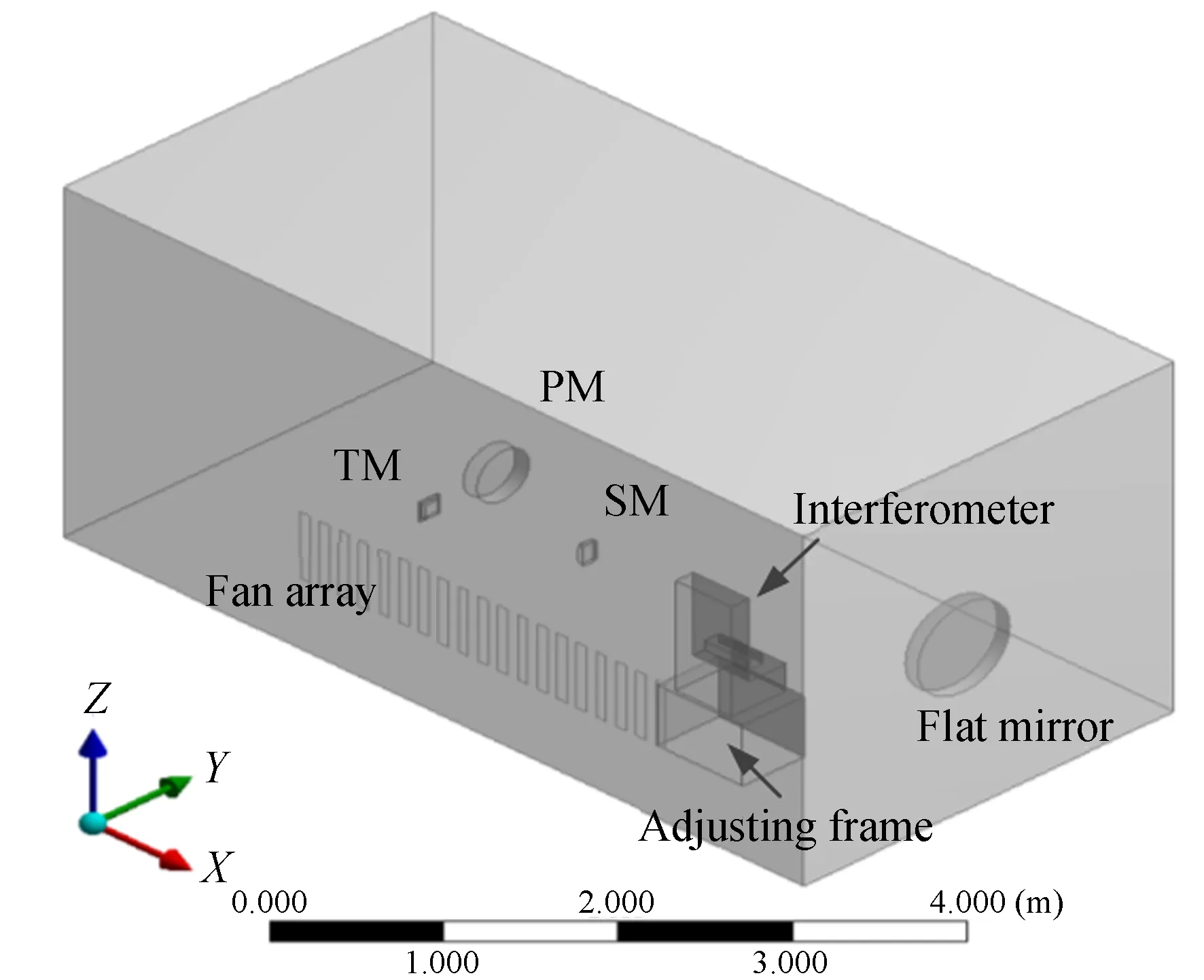
图2 计算流域及坐标系定义

然后，利用计算流体动力学工具Fluent进行仿真模拟[15]。其中，计算流域的尺寸为6 m(长)×3 m(宽)×3 m(高)，主要包括主镜、次镜、三镜、干涉仪及调整架等。风扇进风口位于计算流域——Y面上(气浮平台之外)，每个进风口的尺寸为560 mm×80 mm。计算中，入口速度为1.0 m/s、温度为295 K，气体横掠光学元件、支撑结构外表面后，从计算流域的+Y面流出。初始沿Z方向的最大温差设为4 ℃(底部金属台面温度低，上方空气温度相对较高)。另外，定义了3个Z向横截面，分别为Z=1.275 m，Z=1.555 m，Z=1.835 m，如图3所示，用于分析主动送风之后的温度分布情况。

分别采用1台风扇、5台风扇、10台风扇和20台风扇横掠全光路及主镜截面时，三个Z向横截面处的温度场分布如图4所示，其中虚线方框为检测光路所在的区域，三个横截面内温差的PV值分别为0.755，0.734，0.530和0.458 ℃。可以看出，采用5台风扇与采用1台风扇时空气温差几乎一致，而风扇数量增加至10台时，温差能够得到有效降低；在将风扇数量增加至20台时，虽然能够继续降低温差，但效果已不明显。考虑到检测光路X方向的长度有限，本文的温度场控制方案采用10台风扇进行主动送风。

图3 后处理Z向横截面定义示意图

另外，中间截面(Z=1.555 m)的气流速度场如图5所示。可以看出，采用1台或者5台风扇时，干涉光路内部分区域的气流速度仍然较慢，导致干涉检测数据存在“慢漂”现象；而当风扇数量增加到10台时，干涉检测光路内空气流速较快且更为均匀。此时，气流对波前检测精度的影响转变为一种变化频率较高的随机误差，通过大量测量然后取平均的手段可保证测量精度。

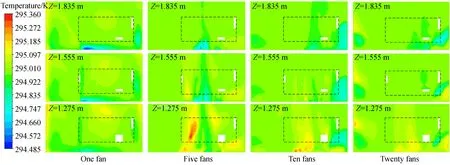
图4 采用不同数量的风扇时三个横截面内的温度分布

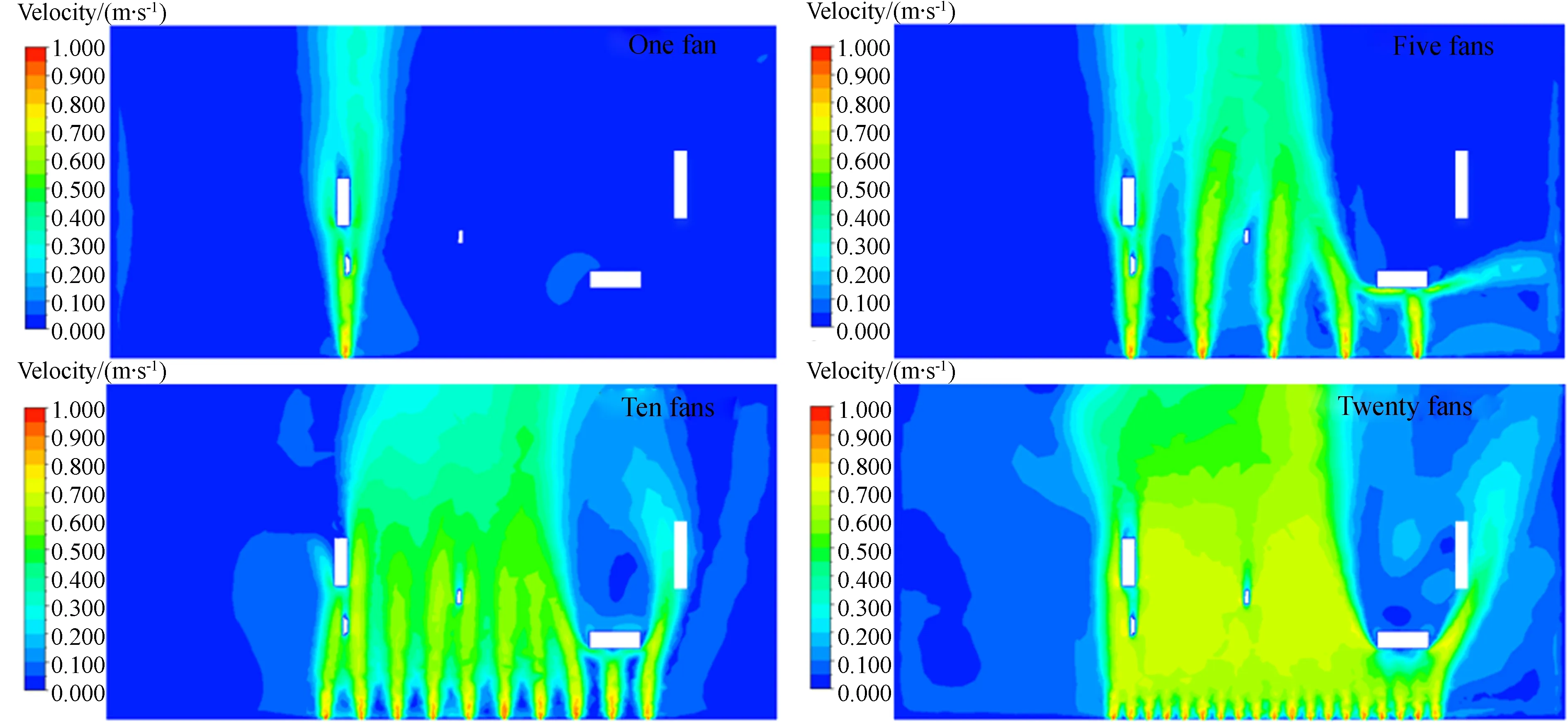
图5 采用不同数量的风扇时气流速度场分布

4 实 验

为验证所提出气流扰动影响抑制方法的有效性，本文搭建离轴三反系统自准直干涉检测光路。将离轴三反系统、干涉仪以及相应的调整机构置于气浮隔振平台上，干涉仪发出的汇聚球面波经过离轴三反系统之后变为平行光，再经过平面发射镜反射之后原路返回，构成自准直回路，如图6所示。

图6 离轴三反系统自准直干涉检测光路实物图

然后，设置由风扇阵列构成的温度场控制装置。将一排风扇(共10只，其中有3只被平面镜挡住未在图中显示)置于气浮平台旁边，出风口与检测光路水平高度一致。

在不进行温度场控制时测量多组波前像差系数。在特定失调工况下，针对某一典型像差系数(考虑到像散为离轴三反失调产生的主要像差类型[16-20]，本文选取第5项条纹泽尼克系数C5，对应0度像散值)，本文共进行7组测量，每组测量数据包含约250次测量值(两次测量之间的时间间隔为5 s)，取平均值作为各组的最终测量值。注意，测量前需要关闭门窗，避免人员走动，且稳定较长时间后再进行测量。

在温度场控制后测量多组波前像差系数。针对相同的失调情况与像差系数类型，打开风扇阵列电源开关，稳定一段时间后，同样进行7组测量。每组测量数据包含约250次测量值，取平均值作为各组的最终测量值。

最后，针对两组测量结果进行分析对比与讨论。通过主动送风进行温度场控制，前后7组像差系数的(C5)测量结果如图7(a)所示。其中，横坐标“时间序列”表示各测量值在各组内所处的测量序号，纵坐标为C5像差系数的测量值，单位为λ=632.8 nm。各组对应的直方图统计结果如图7(b)所示。两种不同条件下各组数据的平均值与标准差如表2所示。

从表2中数据可以看出，在进行温度场控制之前，7次测量值之间偏差较大，标准差为0.034λ；而进行温度场控制之后，7次测量值之间标准差很小，约为0.005λ。这充分说明，在多次测量取平均值的条件下，利用本文方法进行温度场控制可使测量结果稳定性显著提升，说明气流扰动对测量结果的影响被有效抑制。从图7(b)中能得到相似结论，主动送风后直方图峰值位置基本一致，而主动送风前直方图峰值位置存在较大变动。

表2 温度场控制前后7组测量值的均值

Tab.2 Average of aberration coefficients for 7 measurement sets with and without control of temperature field

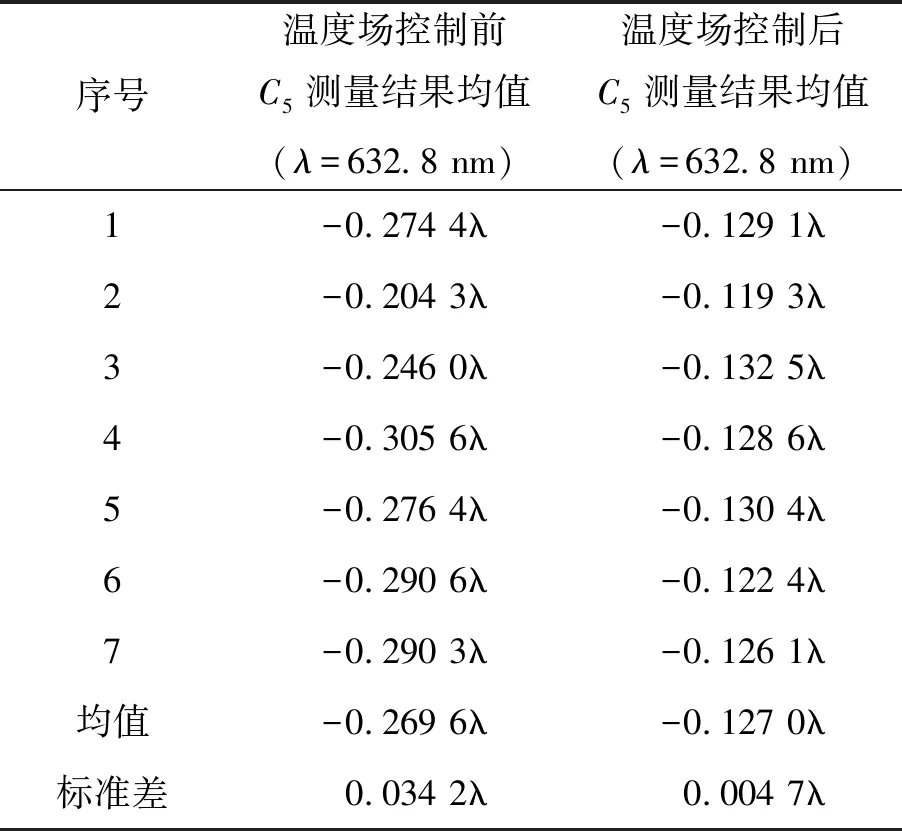
序号温度场控制前C5测量结果均值(λ=632.8 nm)温度场控制后C5测量结果均值(λ=632.8 nm)1-0.274 4λ-0.129 1λ2-0.204 3λ-0.119 3λ3-0.246 0λ-0.132 5λ4-0.305 6λ-0.128 6λ5-0.276 4λ-0.130 4λ6-0.290 6λ-0.122 4λ7-0.290 3λ-0.126 1λ均值-0.269 6λ-0.127 0λ标准差0.034 2λ0.004 7λ

从图7(a)可以看出，在没有进行送风的条件下，虽然在测量之前静候较长一段时间以让气流趋于平稳，但从各次实验数据来看，测量结果依然表现为“慢漂”与“跳变”的结合(在缓慢周期性变化的基础上，存在一定幅度的数据跳变)。这是因为室内热源与热沉一直存在，且空气热惯性小，易流动，任何的轻微扰动都会引起空气的运动，同时伴随热量的传输，因此现实中的“稳态”难以达到。

另一方面，由图7(a)可知，在进行温度场控制之后，室内空气温度场被搅乱，室内存在的“空气包”被打碎，数据呈现随机跳变，无“慢漂”现象。虽然此时数据之间存在一定的跳变，但平均值却存在较高的稳定性，多次测量取平均值能够大大降低气流扰动的影响。

图7 主动送风前后7组波像差系数测量数据及其直方图

本文继续对温度场控制前后各7组数据进行分析，结果如图8所示(彩图见期刊电子版)。其中蓝色数据为温度场控制之前所有测量值，红色数据为温度场控制之后所有测量值。

从图8(a)可以看出，温度场控制之前，受气流扰动影响，测量数据表现为周期性“慢漂”与随机“跳变”的结合，与单组分析结果相符。在该情况下，即便多次测量取均值，也不能消除气流扰动的影响。因为均值受随机“跳变”的影响较小，但受周期性“慢漂”的影响很大。而在温度场控制条件下，数据表现为一个固定值附近的随机变化，多次测量数据的均值很稳定，受气流扰动的影响较小。

从图8(b)直方图统计中可以看出，两种条件下测量值(均值)之间存在系统性误差，约为0.14λ。该误差主要由光学系统下方冰凉台面与系统上方空气之间的温差产生，无法通过多次取平均的手段消除。静态情况下，竖直方向温差产生的系统误差能与光学系统自身存在的像差叠加或补偿，叠加或补偿取决于系统自身的像差方向，叠加或补偿的量取决于竖直方向温差的大小。该系统误差随温度分布的变化而变化，难以准确标定。而吹风条件下，温度场被扰乱，该系统误差不再存在，取平均之后，各像差系数值接近真值。

从图8(c)可以看出，温度场控制之前，测量数据频谱(除去零频)以低频成分为主，对应图8(a)中呈现一定周期性“慢漂”的数据成分，高频成分含量较少；而在温度场控制之后，测量数据频谱(除去零频)在频域均匀分布，与白噪声频谱类似。该类型随机误差可通过多次取平均消除。

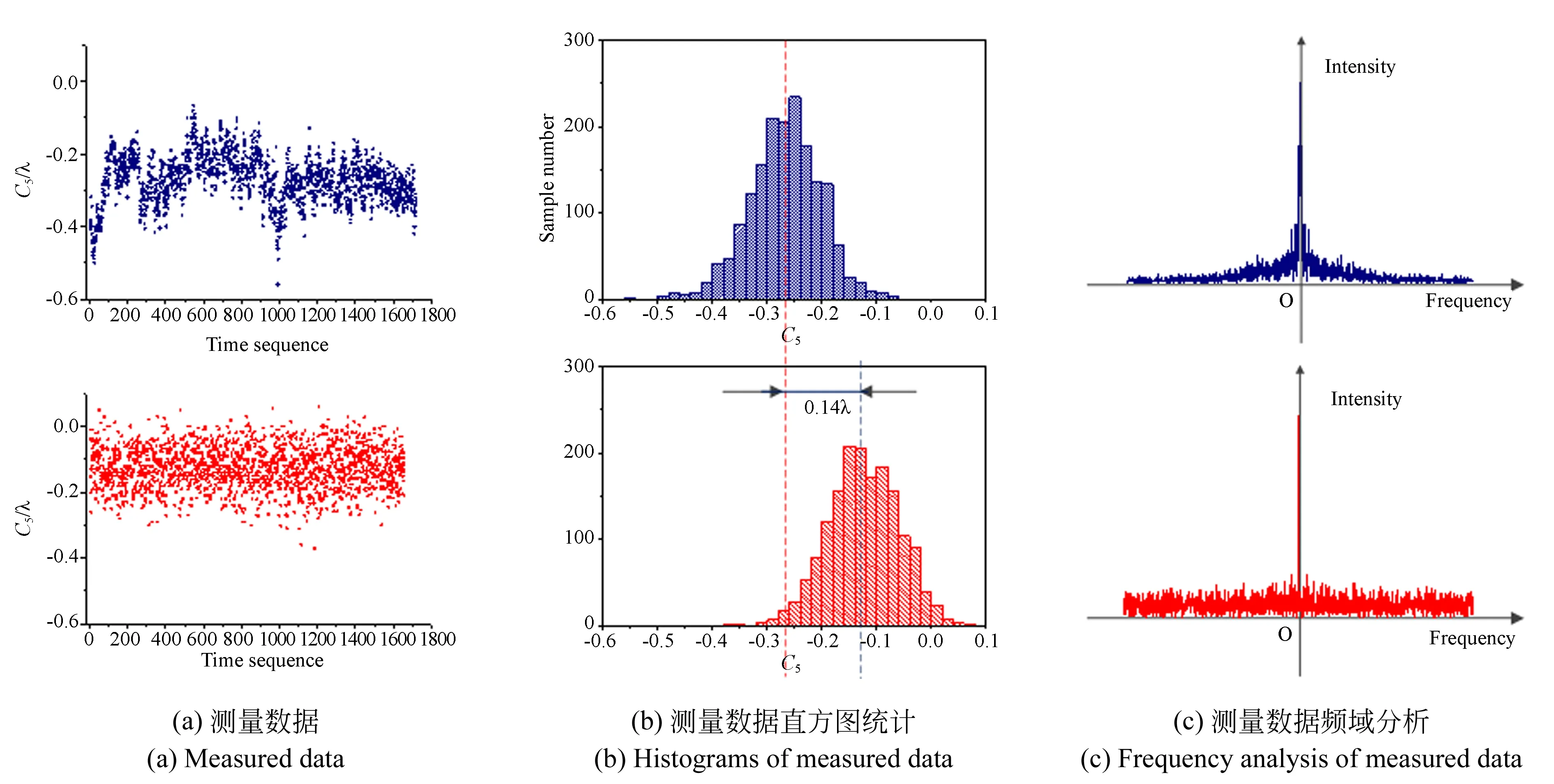
图8 主动送风前后波像差系数测量数据分析

5 结 论

气流扰动将引起干涉检测光路中空气折射率变化，引入未知波前测量误差，这对于大口径、长焦距光学系统波前检测精度的影响尤为严重。为抑制气流扰动影响，本文结合口径为500 mm、焦距为6 000 mm的离轴三反望远镜检测光路及它所处的环境条件，基于流体力学理论，通过仿真建模提出一种利用风扇阵列主动送风的室内温度场控制方法，并进行相关实验验证。对温度场控制前后7组实际测量像差系数(每组包含约250个单次测量数据)之间的标准差进行比较，结果表明，7组像差系数测量值(约250个单次测量平均值)之间的标准差由0.034λ减小到0.005λ(λ=632.8 nm)，由此说明本方法可有效抑制气流扰动对于光学检测精度的影响。

本文以真实离轴三反系统波前检测过程为研究对象，所采用的分析建模方式以及主动送风方式对于提高非真空条件下大口径、长焦距光学系统的波前检测精度具有重要的参考意义。需要注意的是，本方法中风扇为等距离摆放，其送风速度与位置并没有经过优化，最终流场与温度场的均匀性有待进一步提高。从图7与图8中仍能看出，加入风扇后单次数据跳动比较大(虽然大量取平均之后数据较稳定)，PV值大约在0.3λ。在未来的工作中，将对风场设置进行进一步优化与改进，包括对风扇流场与分布位置方案的对比研究等，从而将气流扰动影响抑制到更低水平。