空间点的多视图DLT三维定位

赵祚喜，冯 荣，朱裕昌，谈 婷

(华南农业大学 工程学院，广东 广州 510642)

1 引 言

在航空航天、机械制造、汽车装配等领域，各种复杂零件的研制、生产和装配、建模、仿真、分析，需要先进的检测技术和测量方法。对于越来越多需要进行空间三维测量的工件，传统的线、面检测方法已不能满足生产需要，因此坐标测量技术将作为几何量测的研究重点[1]。传统的坐标测量方法一般采用全站仪、三坐标测量仪、激光跟踪仪等进行三维关键点的测量，这些仪器每次只能测量很少的点，测量速度相当慢[2-4]。由于基于计算机视觉的三维定位技术具有非接触、无破坏以及高分辨率、测量效率高的优点，已逐渐成为几何量测技术的研究重点[5]。

3D视觉测量系统根据相机是否需要固定分为大致分为两种测量模式：一种是摄像机固定式的三维测量，即摄像机固定，操作人员手持光笔，将光笔低端的测针接触物体表面上的被测点，摄像机系统通过光笔上镶嵌的多个光学特征点，求解出光笔的空间位姿参数，由于测针的几何位置已知，被测点的三维坐标即可被精确测量出来；另一种是摄像机移动式的三维测量，事先在被测物体表面粘贴标记点，利用手持式高分辨率数码相机在多个位置对被测物体进行拍摄，测量软件对图像自动进行处理并计算出标记点的空间坐标，实例是各种手持3D扫描仪。

在3D视觉定位领域的研究和应用很多。赵永国[6]等在移动机器人避障过程中为获取障碍物在现实世界坐标系下的三维坐标，利用MATLAB与Triclops SDK数据库，开发了一套基于双目视觉的移动机器人避障系统，实测数据表明该套系统具有不错的避障表现；解则晓[7]等为了对车间生产工件实现高精度、大尺寸的三维坐标现场测量，设计了一套光笔测量系统，该系统由两台面阵CCD摄像机、光笔、支架及一台笔记本电脑组成，通过试验测试了该系统在有效视场范围内的测量精度，基本满足要求不太高的大尺寸现场测量；董英华[8]等为提高其研发的光笔式视觉坐标测量系统的测量精度，采用改进的Tsai标定法实现摄像机的高精度标定，通过数学平均思想提高了测头中心的稳定性及算法的收敛速度；孔筱芳[9]等提出一种双目摄像机标定及空间坐标重建方法，采用了高精度GPS代替2D或3D靶标，与传统的3D靶标标定方法相比，其空间重建坐标相对距离误差从1.56%减少到0.52%，具有较高的空间坐标重建精度，但GPS不便于安装到被测物体表面点上，不满足实际的应用场景。

国内外一些公司已开发出成熟的3D测量产品，国外的有挪威Metronor公司的SOLO系统、美国GSI公司的V-STARS系统和Aicon公司的ProCam系统等[10]，国内的有北京天远三维科技公司的DigiMetric三维摄影测量系统和Robot动作捕捉系统等。SOLO系统主要由相机、测量光笔及测针、笔记本电脑及测量软件组成，该系统可实现30 m的范围测量，长度测量精度为25 μm，还可以测量600 mm深度的隐藏点[11]；V-STARS/S系统由1套测量型数码相机、1台笔记本电脑(含系统软件)、1根基准尺、1根定向棒、1组人工特征标志点组成，10 m范围的坐标测量精度达到0.044 mm[12]；DigiMetric三维摄影测量系统是在被测物体表面粘贴若干标记点，利用手持式高分辨率数码相机在多个位置对被测物体进行拍摄，将拍摄所得图像导入到计算机中，DigiMetric测量系统软件对图像自动进行处理并计算出标记点的三维坐标，具有测量环境不受限制，测量范围不受限制，操作简单方便等优点，坐标测量精度≤0.1 mm/4 m。

以上的方法往往需要昂贵的仪器、专门的设备因而应用受到限制，例如能同时定位的点数、二次开发能力等的限制，难以在一般的实验室推广使用。本文提出一种不需要昂贵仪器的物体点世界坐标系3D定位方法。该方法基于直接线性变换(Direct Linear Transformation，DLT)的物体上点的世界坐标系下的三维定位方法， 适用于单台相机移动获取的多视图实现的静态结构体点的定位，也适合于多台相机同时拍摄获取的机器上点的三维动态定位。根据空间几何线-线交会原理，利用最小二乘法实现空间点的世界坐标测量，与传统的测量法相比，该方法能够实现任意个点的3D世界坐标测量，而且相机位置可移动，使用方便。

2 基于DLT方法的相机标定及物理点多视图3D定位原理分析

2.1 DLT相机标定

图1 小孔成像模型示意图

相机标定的基本方法是通过环境(有专门的几何形状已知的标定对象或无专门的标定对象)来确定相机几何参数的过程，是计算机3D视觉应用的首要步骤，按照使用的标定对象的不同可分为3D，2D，1D及无标定对象[13]。DLT标定方法是一种基于3D标定对象的相机标定方法，即将标定对象上每一个已知控制点(3D世界坐标已知)和相机图片上的对应的成像点(图像坐标系下2D像素坐标已知)建立线性模型(式(2))，将相机内外参、几何失真参数视为未知数，设置多个控制点使所列的方程数不小于未知数数量，再利用最小二乘法实现这些参数的线性估计(不使用旋转矩阵各个元素之间的非线性约束)，原理简单计算工作量小[13-14]。本章有关DLT方法参考了文献如下[15]，DLT相机标定方法的完整介绍[16]。图1为小孔成像模型示意图，在相机标定过程中涉及4个坐标系及3次坐标转换，分别为世界坐标系W到相机坐标系C的转换①，相机坐标系C到图像坐标系I的转换②，图像坐标系I到像素坐标系S的转换③，最终得到像素坐标系S和世界坐标系W间的线性变换关系[17-18]如式(1)所示：

(1)

其中，(ui,vi,1)T为各成像点的像素齐次坐标，b为相机焦距，ku，kv分别为单个像素在u和v方向上的真实尺寸，(u0,v0)为焦点的像素坐标，rij(i,j=1,2,3)为世界坐标系至相机坐标系之间旋转矩阵R中的元素，(xwi,ywi,zwi) (i=1, 2，…，N)为各标定点的3D世界坐标，(x0,y0,z0)为平移矩阵T，表示相机坐标系原点oc在世界坐标系下的坐标，zci(i=1, 2…N)为各标定点在相机坐标系Z方向上的坐标。

将式(1)展开得式(2)：

ui-u0=

vi-v0=

(2)

将式(2)整理为如下式(3)，使得式(3)中像素坐标(ui,vi)值只取决于标定点的世界坐标(xwi,ywi,zwi) (i=1, 2，…，N)及11个包括相机内外参数的常数参数Lk(k=1, 2，…，11)。

(3)

参数L1～L11可用内外参数表示为如式(4)：

(4)

其中：bu=b/ku，bv=b/kv，D=-(x0r31+y0r32+z0r33)。

将式(3)写成矩阵形式：

(5)

相机标定中，需要设置N(N≥6)个已知三维坐标的控制点，故式(5)中含有2N个线性方程，令:

(6)

则式(6)可表示为求解非齐次线性方程组的矩阵形式Ax=b，采用最小二乘法可求解出未知量x，即：

x=(ATA)-1ATb.

(7)

包含内外参数的Lk(k=1, 2,…,11)求解出后，需要通过式(4)来求解16个内外参数，包括4个内参数bu,bv,u0,v0和12个外参数rij(i,j=1,2,3)，T=[x0y0z0]T，其中外参数rij(i,j=1,2,3)形成的矩阵R3×3为正交旋转矩阵。这样就完成了相机的内外参数DLT法的标定。显然如果是多台相机实现多视图测量，则每台相机要经过上述步骤实现标定；如果是单台相机移动位置实现的多视图测量，则没移动一个位置均要按上述方法标定一次。

2.2 物理点的多视图3D定位

如前所述，多视图包括单台相机移动位置拍摄同一个场景得到多视图，也指多台相机同时拍摄获取多视图。前者适合静态测量场合后者适合于动态测量场合。图2为物理点的多视图的3D定位(坐标重建)系统结构和原理示意图。

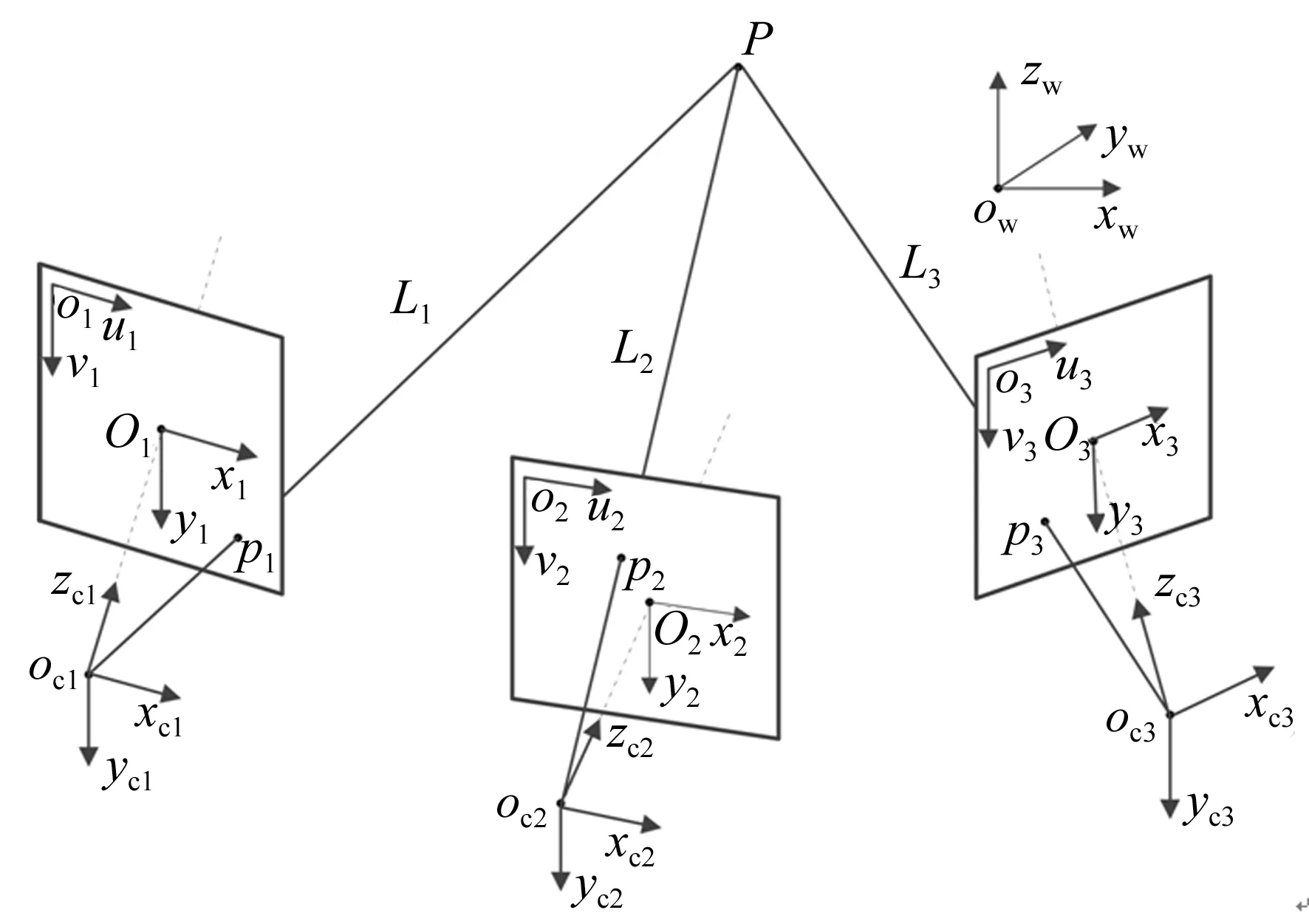
图2 多视图的坐标重建示意图

对于每个视图下的相机而言，如果光心和像点已知，可唯一确定过测量点的一条直线，依据空间几何线-线交会原理，可以对测量点进行交会定位，由于镜头畸变、像素坐标提取精度、标定点坐标误差的存在，使得相机多角度确定的各条直线异面，不会相交于同一测量点，因此本文通过最小二乘法来求解被测目标点的空间坐标，假设空间中任意一点P(xw，yw，zw)在相机3个视图中对应的成像点分别为p1(u1，v1)，p2(u2，v2)和p3(u3，v3)，3个视图对应的相机参数Li(i=1，2，…，11)可由式(7)求解得出，由式(3)，可得到如下方程：

(8)

单个视图可列出2个线性方程，则3个视图可列出关于(xw，yw，zw)的6个线性方程，转换为矩阵形式，有：

(9)

采用最小二乘法x=(ATA)-1ATb即可求解出被测点P的坐标(xw，yw，zw)。

为评价定位结果提出以下评价指标。将获得的空间重建点P(xw，yw，zw)与其在世界坐标系下3D坐标真值(xq，yq，zq)进行比较，得到空间点P重建坐标在X,Y,Z方向上的误差dX,dY,dZ，有：

(10)

由式(11)可得空间重建坐标相对距离误差为：

(11)

2.3 DLT多视图物理点3D定位基本步骤

本文提出的DLT多视图物理点世界坐标系3D定位的基本步骤总结如下：

(1)建立世界坐标系下的3D标定对象：即确定不少于6个不在同一个平面的控制点并确定世界坐标系下的3D坐标。控制点包络体积尽量覆盖待测点的运动范围，控制点数尽量多且尽量在包络体积中均布；

(2)DLT方法完成相机标定得到L参数(式(7))及相机内外参数(式(4))。多台相机则每台相机要标定，如果是单台相机则没移动一个位置均要标定。见2.1节；

(3)测量待定位物理点对应的图像点的像素坐标，利用上面2)标定求得的各相机(或同一相机不同位置)的L参数，由式(9)求得这些点的世界坐标系的3D坐标。见2.2节；

(4)如果是多相机实现的多视图物理点位置的连续动态测量，假定相机位置不动则返回(3)继续执行直至任务完成；否则返回(2)(即重新标定)继续执行至任务完成。

3 试验设计与数据分析

3.1 试验设备

进行了单相机移动位置实现的多视图多个物理点静态定位试验并与真实结果(全站仪测量得到)进行了比较验证。实验采用美国Vision Research 公司产的Phantom M310高速相机进行图像采集，传感器尺寸为25.6×16.0 mm，分辨率为1 280×800，对应像素大小20 μm×20 μm，镜头焦距24～85 mm可调，拍摄速率采用1 000 frame/s，光圈值为f/2.8；采用瑞典Image Systems公司的TEMA运动分析软件测量图像中标定点及被测点的像素坐标，在这里拍摄的是静态场景，故只需截取视频中的1帧图像导入TEMA软件中进行处理；采用科利达公司产的KTS-462LL全站仪对目标点的三维坐标进行测量，该仪器的测距精度为2+2ppm×5 km，即测量距离为5 km的误差为12 mm，试验在1PJ-3.0型水田平地机上进行，图3为水田平地机的结构示意图。

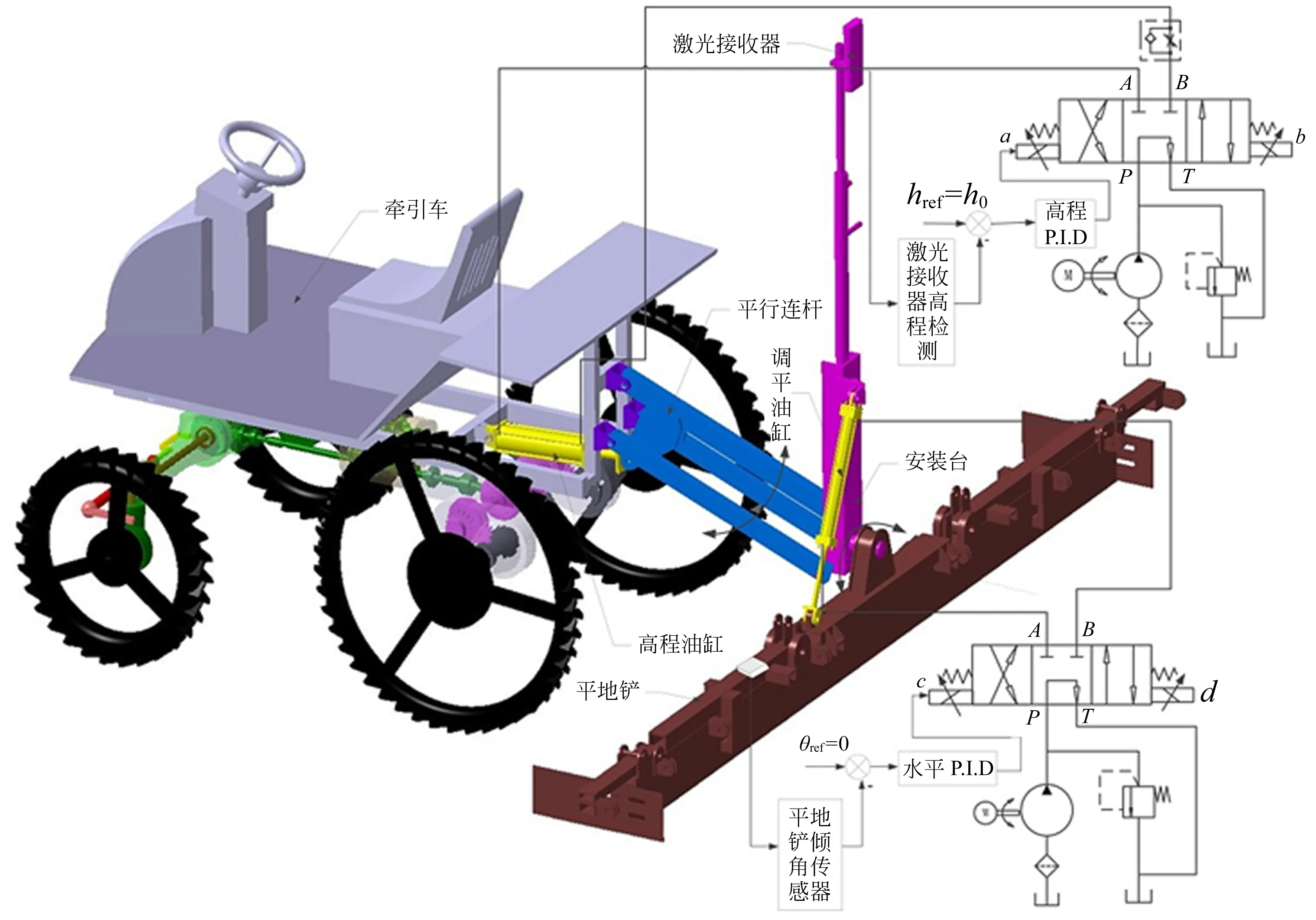
图3 水田平地机结构示意图

水田平地机包括机械系统、液压系统、高程控制系统和水平控制系统四大部分，采用乘坐式井关PG6插秧机的为动力[19-20]，以三点悬挂方式与平地机相连，三条平行连杆一端与插秧机底盘旋转铰链连接(铰接)，另一端与安装台铰接，安装台下端有另一个铰链与平地铲中间连接。安装台与平地铲之间安装有双作用油缸驱使二者之间相对转动实现平地作业中平地铲处于调平状态。

3.2 试验步骤及方法

按照2.3节所述的基本步骤，进行如下操作。由于试验涉及到验证，故具体步骤稍有区别。

(1)设定世界坐标系，设定控制点及待测点

图4为试验平台及试验布置示意图，先将图4(b)中的平地铲置于水平地面，在测台架1上建立世界坐标系ow-xwywzw，在平地铲上粘贴如图所示的不共面的10个十字架形状(对角象限分别为白色和黑色)的控制点(像宝马汽车标志，标志点指该十字的交点)，记录下各标定点在坐标系ow-xwywzw下的三维坐标，在平地铲上另外粘贴20个标记点作为待测点。一般世界坐标系是静止的，控制点宜设置在静止的物体上，而这里是静态试验，控制点和待测点均位于同一刚体(平地铲，水平静置)不会造成问题。

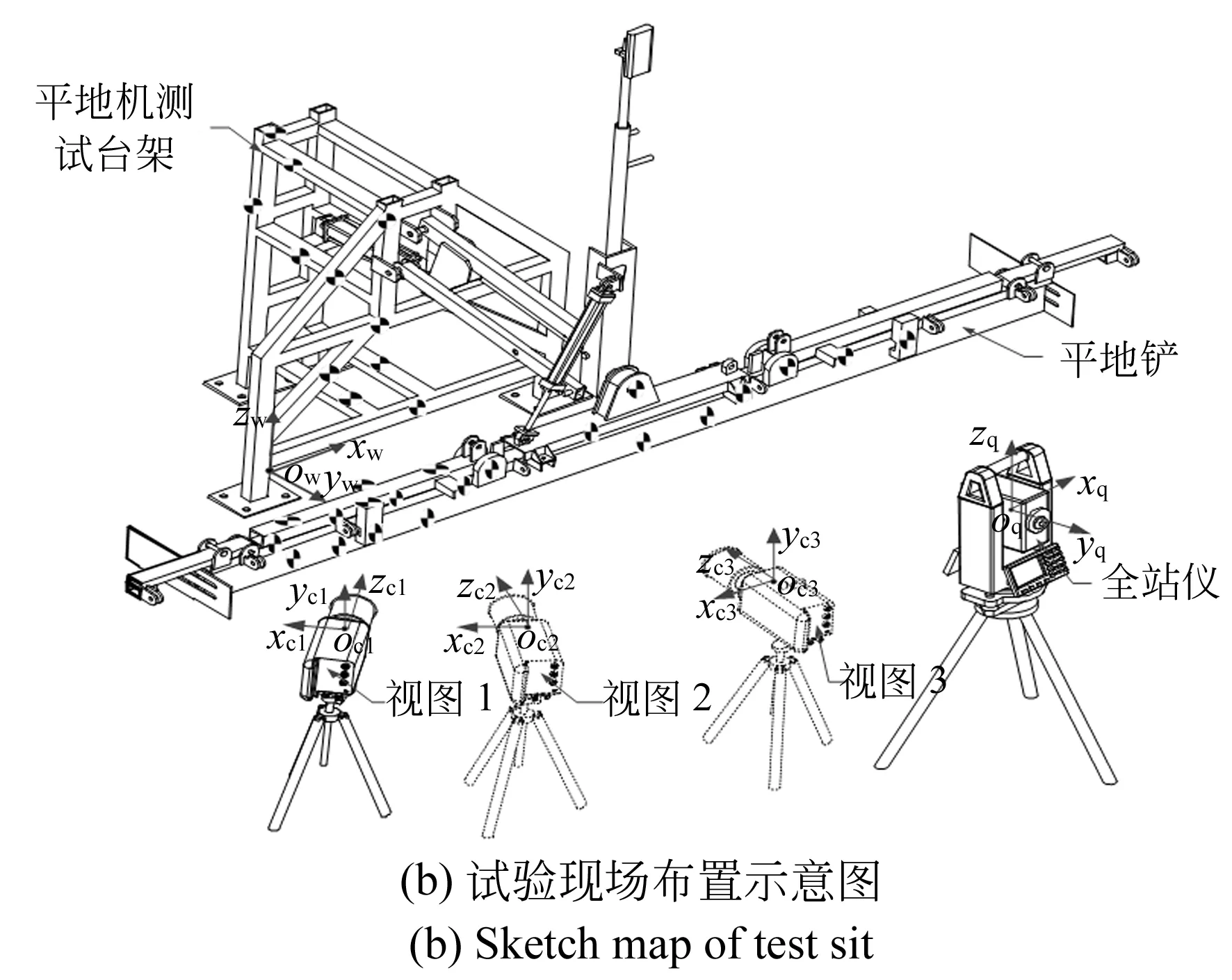
图4 试验平台及现场布置示意图(平地机测试台上的宝马点为标定点；平地铲上的宝马点为待测点)

Fig.4 Test platform and sketch map of the test site(BMW points on test setup for leveler are calibration points; BMW points on land-leveling plow are measured points)

(2)DLT方法完成相机标定得到L参数

调整相机的位置及焦距，使得标定点及待测点在视场中清晰可见，采集此视图1下的图像，记为I1，按相同方法采集视图2和视图3下的图像，记为I2和I3；TEMA软件完成图像标记点的跟踪识别和像素坐标的读取，并按2.1节方法完成各位置下的相机标定。

(3)测量各待定位物理点对应的图像点的像素坐标；

(4)结果验证。采用全站仪测量待测点的世界坐标作为世界坐标系真实3D位置：

①建立全站仪坐标系oq-xqyqzq

将全站仪架设到适宜位置，手动调平，建立以全站仪激光发射中心oq为坐标原点，坐标轴方向与世界坐标系坐标轴方向一致的全站仪坐标系oq-xqyqzq；

②全站仪测量待测点坐标

测量得到这些点在全站仪坐标系oq-xqyqzq下的三维坐标，然后将所有的被测点坐标与测得的世界坐标系原点坐标相减，即可将所有被测点在全站仪坐标系下的坐标转换到世界坐标系下。

3.3 试验数据分析

本实验利用测试台架(平地铲)上粘贴的10个标定点的空间坐标及各标定点在图像Ij(j=1，2，3)的像素坐标，通过最小二乘法及高斯-牛顿迭代法完成各视图下的相机标定，然后根据空间几何线-线交会原理，利用最小二乘法实现被测点的世界坐标测量，表1为部分标定点Pi(i=1,2,…，10)的世界坐标及在图像Ij(j=1，2，3)中的像素坐标信息，表2为部分被测点Qn(n=1,2,…，20)在图像Ij(j=1，2，3)中的像素坐标信息。表3为求得的各视图参数Lk(i=1，2，…，11)，表4为利用高斯-牛顿迭代法求得的各视图相机内外参数，试验采用的各视图相机分辨率均为1 280×800，则像平面中焦点O的理想像素坐标为(640，400)，从表4可以看出，3个视图的相机标定结果中，焦点横坐标最大偏差为65.28 pixel，焦点纵最大偏差为63.36 pixel，这与标定过程中各标定点空间坐标测量误差及对应的像素坐标提取误差有关。

表1 部分标定点的坐标

表2 部分被测点的像素坐标

表3 各视图相机参数Lk求解结果

表4 各视图相机内外参数求解结果

分别利用全站仪与本文方法对平地铲上20个被测点进行测量，并计算各被测点在X,Y,Z方向上的误差dX,dY,dZ，结果如图5所示，其中蓝色折线为被测点在世界坐标系ow-xwywzw下的三维坐标(由全站仪获得)，绿色折线为相机测得的各被测点在X,Y,Z方向上的坐标，红色折线为相机测得的被测点坐标相对于全站仪测得坐标的误差，表5为被测点在X,Y,Z方向上的平均误差，从图5可以看出(彩图见期刊电子版)，相机测得被测点坐标与全站仪测得的坐标位置基本吻合，被测点坐标在X,Y,Z方向上的绝对误差均值为4.19 mm,3.97 mm,3.69 mm，空间相对距离误差为0.81%。

表5 被测点在X,Y,Z方向上的平均误差

Tab.5 Average error of measured points inX,Y, andZdirections

X方向Y方向Z方向Error相机测量0.004 20.004 00.003 70.008 1

图5 被测点的世界坐标在X,Y,Z方向的误差

4 结 论

(1)本文提出的基于DLT的世界坐标系多视图3D定位方法，既适用于单台相机移动获取的多视图实现的静态结构体点的定位，也适合于多台相机同时拍摄获取的机器上点的三维动态定位，能够实现任意多个物理点的世界坐标测量，原理上测量结果不受相机位置影响。该方法不需要专门的仪器设备，对一般的结构和机器系统的测绘、运动分析适用。

(2)在水田平地机上进行了单相机移动位置得到的多视图多物理点静态定位试验。验证采用本方多个目标点进行了世界坐标测量，与全站仪的测量结果相比，该方法测得的坐标在X,Y,Z方向的平均绝对误差为4.19 mm,3.97 mm,3.69 mm，空间相对距离误差为0.81%，满足一般测量精度要求。

(3)为进一步DLT相机标定与物理点的3D定位的精度除了使用更多的控制点、更多的视图等措施[15]外，还需要对相机的径向和切向失真进行校正，这可以在DLT标定步骤中对失真参数进行标定，此时需要使用16个L参数，需要的不共面的控制点为8个[15]。此外Matlab有相机标定工具箱，借助该工具箱可以验证本方法第2步得到的相机标定结果。