大行程快速反射镜的结构设计及带宽特性
陈国真,徐斯强,刘品宽,丁 汉
(上海交通大学 机械与动力工程学院,上海 200240)
1 引 言
快速反射镜(Fast Steering Mirror, FSM)是用于光源和目标之间用以改变光束指向的装置,广泛应用于成像系统、激光武器和空间光通信领域[1-4]。目前,基于柔性机构的FSM得到了广泛的研究,因为相比于刚性结构,柔性机构具有无摩擦、无装配间隙、运动精度高等优点[5]。
FSM一般由音圈电机和压电陶瓷驱动[6-11]。相比于压电陶瓷,音圈电机可以实现毫米级的运动行程,基于音圈电机驱动的FSM可以实现更大的偏转角度。然而,传统机构中的音圈电机的动子会随着FSM的运动而发生相应的偏转,动子末端会有较大的横向位移。由于音圈电机的气隙较小(气隙和输出力成反比),当FSM行程较大时,动子末端会和定子碰撞[12]。因此,基于音圈电机驱动的FSM为了实现大行程运动,必须消除动子的横向位移。
对于运动控制系统,机构的共振模态会降低闭环系统的稳定裕度,从而限制了高增益反馈控制器的使用,因而影响了系统带宽的提高[13]。陷波滤波器是消除系统共振模态的有效方式,根据共振模态的频率和阻尼比即可设计相应的陷波滤波器[13-16]。为了补偿模型误差并提高抗干扰能力,采用比例积分(PI)控制器来实现闭环控制[16]。然而,当柔性机构的运动行程较大时,力-位移关系呈现出明显的非线性[17-18]。机构的刚度随运动位置的增加而增大,从而导致共振频率相应的增大。若采用常值陷波滤波器,即共振频率为常数,系统在不同位置处的带宽性能会有较大差异。因此,对于大行程运动的FSM,采用常值陷波滤波器已不能有效地消除随位置而变化的共振模态的影响。
本文设计了基于音圈电机驱动的新型FSM来实现大行程运动,采用柔性解耦机构来消除电机动子的横向位移。采用变值陷波滤波器来消除随位置而变化的共振模态的影响,即将共振频率表示为FSM运动位置的函数,并配合PI控制器实现闭环控制。通过仿真分析和实验比较了采用常值和变值陷波滤波器时系统的带宽性能,验证了在运动行程较大的FSM系统中设计变值陷波滤波器的必要性和有效性。
2 结构设计
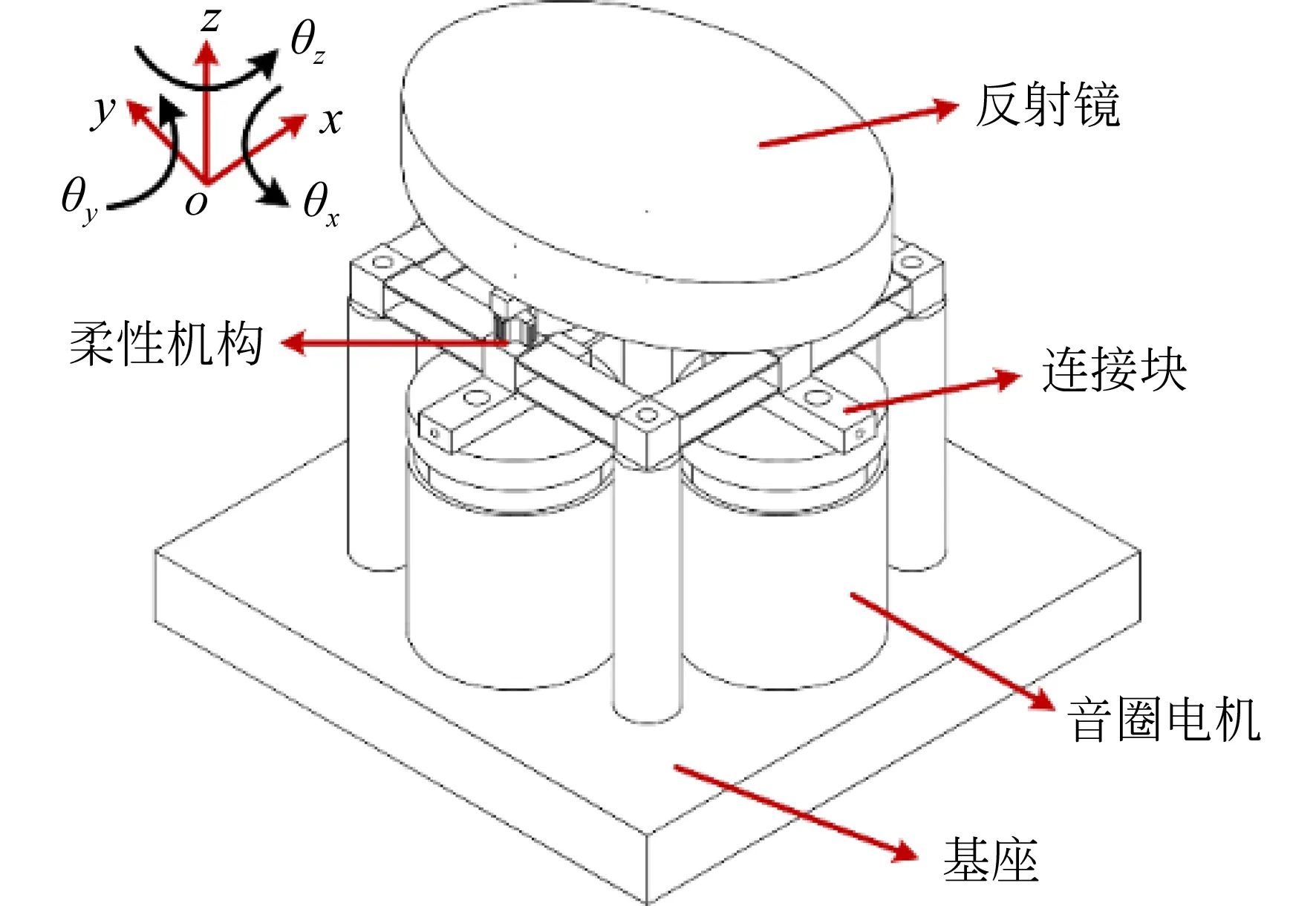
图1 快速反射镜的机械结构
FSM的结构设计如图1所示。FSM由反射镜、4个音圈电机、基座和柔性解耦机构组成。反射镜为椭圆,尺寸为Φ100×Φ70.7×15 mm(长径×短径×厚度)。柔性解耦机构由平动板、解耦板和转动板组成,如图2所示。FSM由4个音圈电机驱动,每两个电机为一对(一个往上推,一个往下拉)驱动FSM来实现绕x(y)轴的转动。当4个音圈电机同时往上推或往下拉时,FSM即可实现沿z轴的平动。平行四杆机构由4个平动板组成,实现沿z轴的平动,同时约束其它自由度的运动。电机沿z轴的竖直运动通过转动板转化为FSM的旋转运动。解耦板可以实现绕x(y)轴的转动,电机动子的横向位移可转化为解耦板的转动。因此,通过柔性解耦机构可以消除电机动子的横向位移来实现FSM的大行程运动。
3 实验系统搭建
FSM的柔性机构通过电火花线切割技术进行加工,其结构参数如表1所示。为便于设计和加工,解耦板和转动板的结构参数相同。利用线性驱动器(LA-210s-02-RA,VREDAN,Inc.)驱动音圈电机(LVCA-038-038-01, MOTICONT, Inc.)来实现电机沿竖直方向的运动,音圈电机的性能参数如表2所示。采用光栅尺(CE300-40,MicroE,Inc.)来测量FSM的输出位移。光栅尺的分辨率为1 μm。将dSPACE-DS1103作为控制器来实现FSM系统的运动控制。实验平台系统如图3所示。
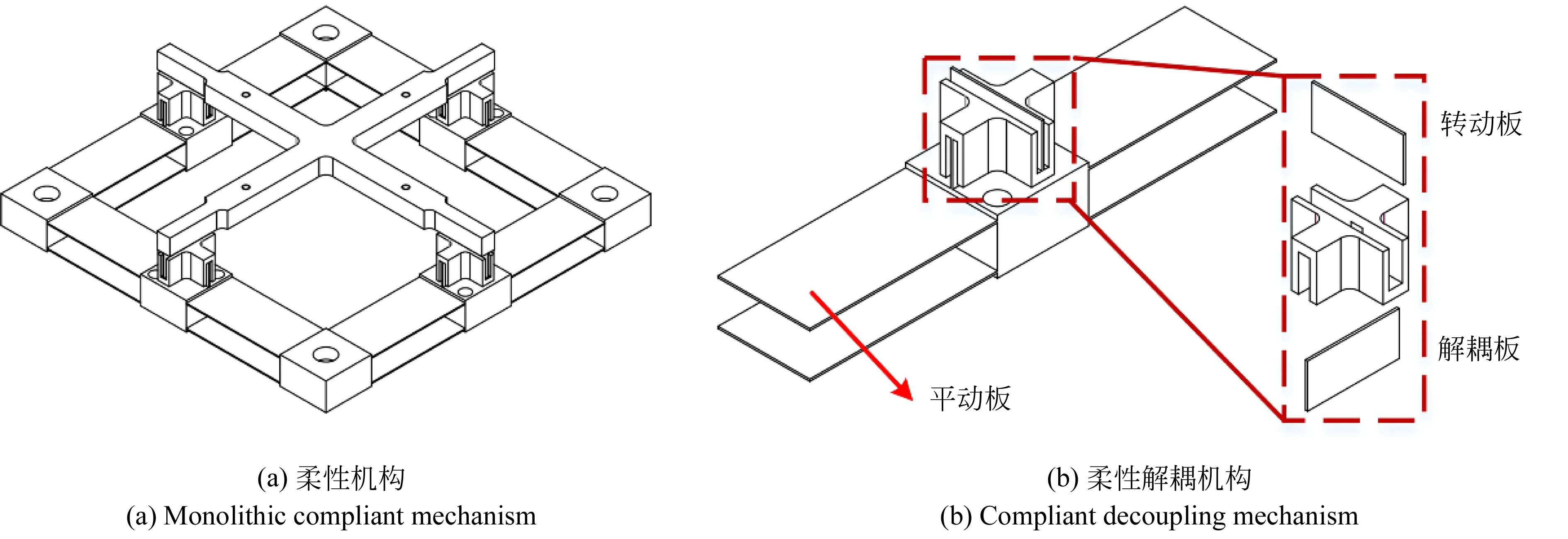
图2 快速反射镜的柔性机构

图3 基于音圈电机驱动的快速反射镜实验平台搭建
表1 柔性机构的结构参数
Tab.1 Structural parameters of compliant mechanism

(mm)
表1中,L1,L2,b1,b2和t1,t2分别表示平动板和转动板(解耦板)的长度、宽度和厚度。

表2 音圈电机的性能参数
4 控制器设计
FSMθx和θy轴的控制器设计原理一样,因此,本节以θx轴为例进行阐述。首先,通过实验测试得到FSM在旋转运动时的力-位移关系。然后,针对FSM的旋转运动进行动力学建模,得到其开环传递函数。最后,计算得到FSM的共振模态与旋转角度的关系,并据此设计相应的变值陷波滤波器。
4.1 力-位移非线性特性
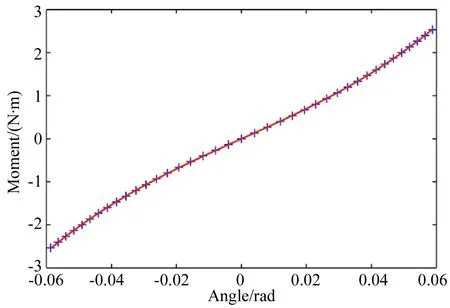
图4 θx轴力-位移关系
当柔性机构实现大行程运动时,其力-位移关系呈现出非线性特性。一般来说,随着位移的增大,柔性机构的刚度逐渐变大,从而导致系统的动力学模型发生变化。因此,要实现对大行程FSM的控制,必须得到其力-位移的非线性关系。经实验测试,FSMθx轴的力-位移关系如图4所示。力和位移的关系可表示为:
Mx=2.73×103θx3-0.82θx2+33.91θx-2.13×10-3,
(1)
对式(1)求导,即可得到旋转刚度和位移的关系,如下所示:
Kx=8.19×103θx2-1.64θx+33.91.
(2)
综上所述,FSM在大行程运动时,力-位移关系呈现明显的非线性,其旋转刚度随位移的增加而增大。
4.2 动力学建模
FSM的动力学方程可表示为:
2rkii(s)-Kθ(s)=s2Jθ(s),
(3)
其中:r和K分别表示FSM的旋转半径和旋转刚度;ki和i分别表示音圈电机的力常数和电机电流;J和θ分别表示FSM的转动惯量和转动角度。
J=2r2(m1+m2)+J1,
(4)
其中:m1和m2分别表示音圈电机动子和连接块的质量;J1为FSM的转动惯量。
根据基尔霍夫定律,可以推导出音圈电机的电学模型得到:
U(s)=(R+Ls)i(s)+kirθ(s)s,
(5)
其中:U表示音圈电机两端的电压;R和L分别表示音圈电机的电阻和电感。
控制信号u经dSPACE放大十倍后即为驱动器的输入信号,同时将Varedan驱动器近似为电流放大环节,即可得到dSPACE控制指令u和音圈电机两端电压U之间的关系:
(6)
根据式(3)~式(6),FSM的传递函数可表示为:
(7)
其中:
4.3 变值陷波滤波器设计
FSM的开环传递函数为三阶系统,包括一个二阶阻尼震荡环节和一个一阶惯性环节。二阶阻尼震荡环节的共振会导致系统稳定裕度的降低,从而限制了高增益反馈控制器的应用。因此,陷波滤波器被广泛地用来消除系统共振模态的影响。
陷波滤波器可表示为:
(8)
其中ξ和w0分别表示系统的阻尼比和共振频率。
陷波滤波器是一种特殊的带阻滤波器,将带阻滤波器的阻带改成一个频率点即为陷波滤波器。常值陷波滤波器只在目标频率处具有幅值衰减的作用,在其他频率点处基本没有影响。然而,根据4.1和4.2节可知,本文设计的FSM的共振模态随运动位置的变化而变化。由式(7)可得到FSM的共振频率与旋转角度的关系:
ωx=3.60×104θx2-7.06θx+339.17.
(9)
因此,必须采用变值陷波滤波器来消除系统随运动位置的变化而改变的共振模态的影响,即将式(8)中的固定值w0替换为式(9)所示的wx。
在零点位置处,根据开环传递函数得到的阻尼比为0.108 4。相比于共振频率的变化,阻尼比的变化对闭环带宽的影响可忽略不计。因此,在不同位置处将阻尼比近似为常值0.108 4。
综上所述,变值陷波滤波器可表示为位置的函数,即有:
(10)
采用PI控制器来实现整个系统的闭环控制。PI控制器可表示为:
(11)
5 仿真分析
采用Matlab软件分别对常值和变值陷波滤波器进行仿真分析,从而验证变值陷波滤波器的必要性和有效性。
根据式(10),常值陷波滤波器可表示为 :
(12)
PI控制器可表示为:
(13)
将式(12)所示的滤波器作为常值陷波滤波器来消除共振模态的影响,分别得到系统在零点和25 mrad处的频率响应,如图 5所示。
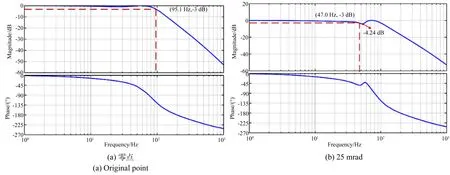
图5 采用常值陷波滤波器时θx轴在不同位置处的带宽
采用常值陷波滤波器时,系统在零点处的带宽为95.1 Hz;当系统运动到25 mrad时,系统的频率响应在共振频率处有一个明显的衰减,为-4.24 dB。因此,系统在25 mrad处的带宽大幅度降低,为47.0 Hz。
采用式(10)所示的变值陷波滤波器来消除共振模态的影响,分别得到系统在零点和25 mrad处的频率响应,如图6所示。采用变值陷波滤波器,系统运动到25 mrad时,它在共振频率处的频率响应并没有明显的衰减,系统带宽为91.2 Hz。
综上所述,FSM沿θx轴运动时,变值陷波滤波器可以消除共振模态的影响。
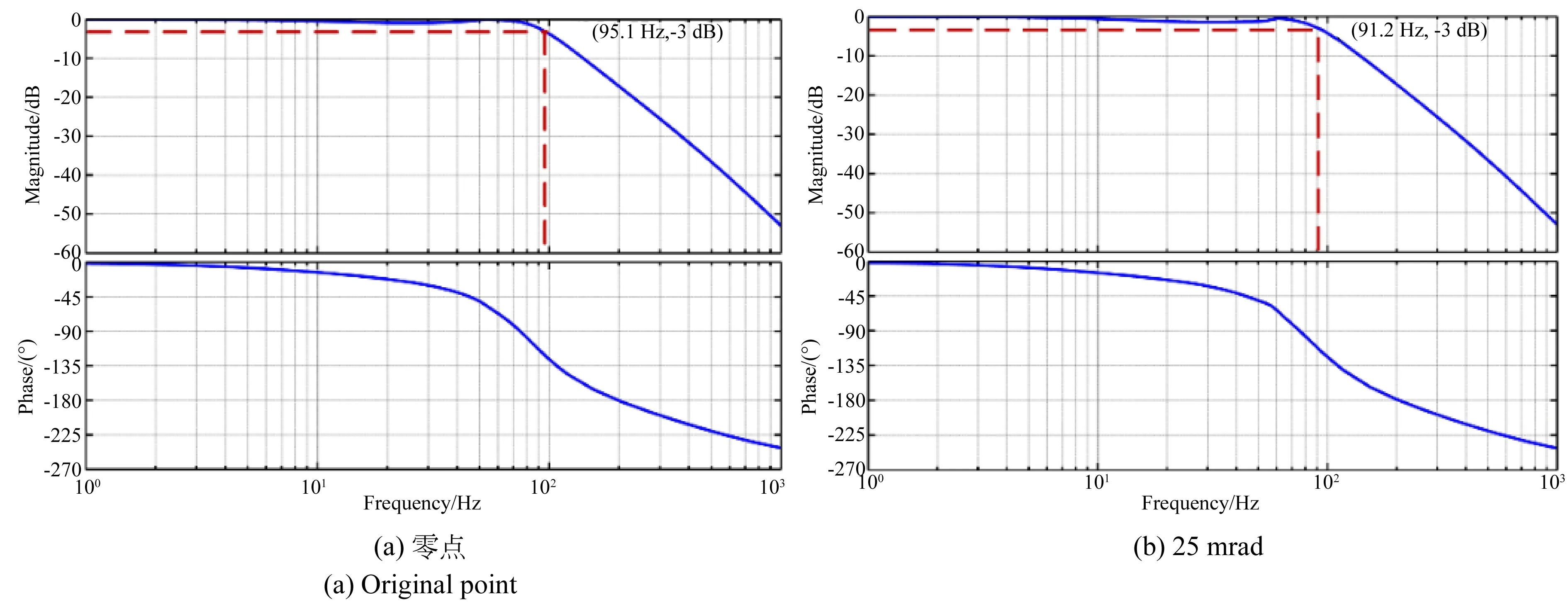
图6 采用变值陷波滤波器时θx轴在不同位置处的带宽
6 实 验
当采用常值和变值陷波滤波器作为FSM系统的控制策略时,这里分别测试了系统在不同位置处的闭环带宽性能,并通过对比实验验证了变值陷波滤波器的必要性和有效性。
6.1 常值陷波滤波器
在dSPACE中输入扫频信号,通过辨识得到θx轴的开环传递函数,拟合和实验得到开环传递函数的频率响应结果,如图 7所示。
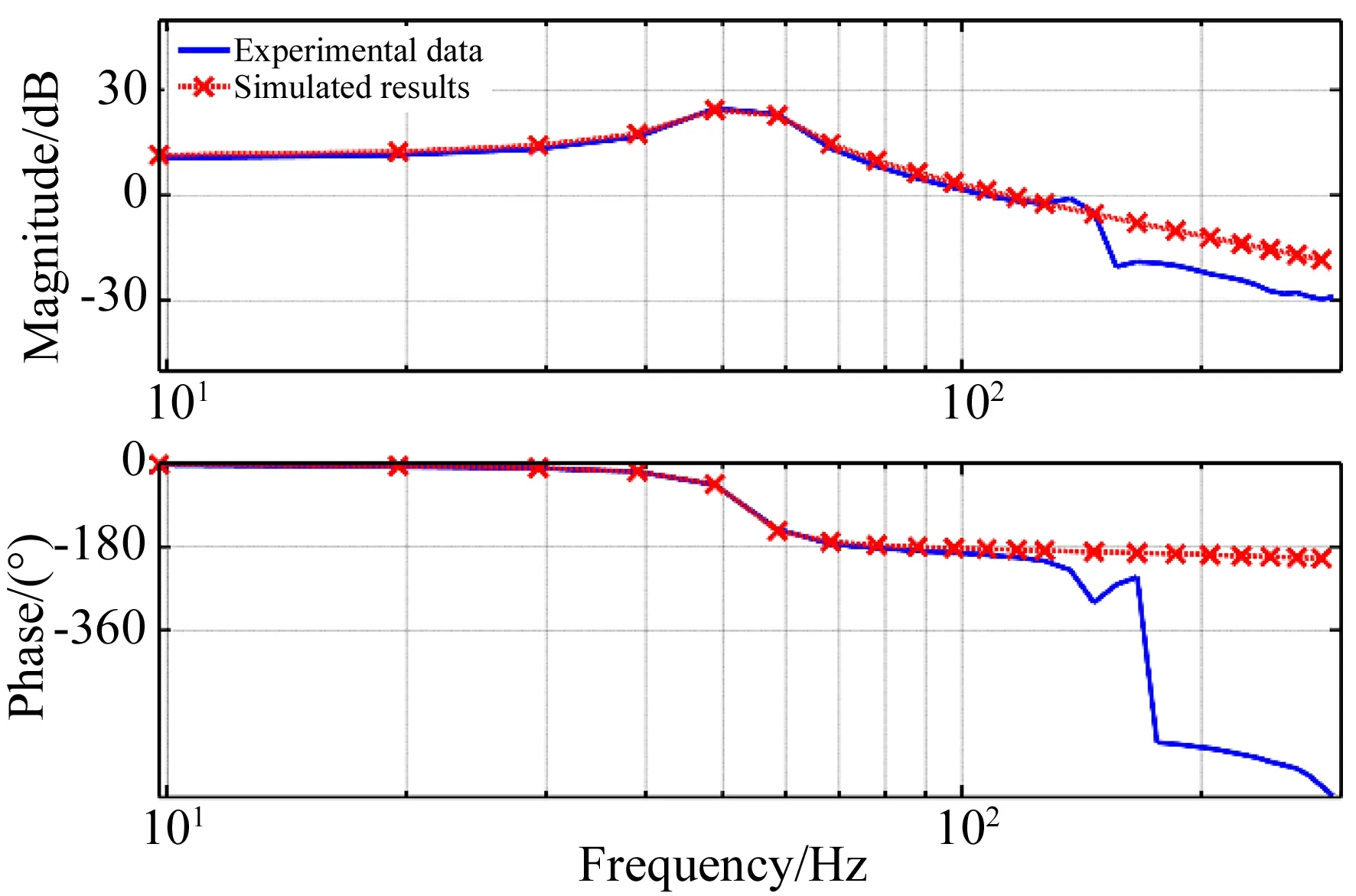
图7 θx轴开环辨识
辨识结果可表示为:
(14)
由式(14)可知,θx轴的共振频率和阻尼比分别为:
ωx=336.15 rad/s,ξ=0.077 47.
(15)
根据式(8)设计相应的常值陷波滤波器得到:
(16)
PI控制器可表示为:
(17)
采用式(16)设计的常值陷波滤波器和式(17)设计的PI控制器对FSM进行闭环控制,测试了θx轴在不同位置处的带宽性能,如图8所示。同理可得到θy轴在不同位置处的带宽性能,如图 9所示。
根据实验结果可知,随着运动位置的增大,FSM在共振频率附近点处的频率响应出现明显的衰减。在零点处,θx和θy轴在共振频率附近点处频率响应的最小值分别为-0.56 dB和-0.69 dB,但随着位置的增大,其值一直减小。当系统运动到21.2 mrad时,θx和θy轴频率响应的最小值分别约为-3.93 dB和-4.45 dB。
系统在共振频率附近点处频率响应的最小值的变化直接影响了其带宽性能。如表 3所示,当系统的运动位置小于15.2 mrad时,θx和θy轴的带宽分别为95 Hz和110 Hz左右。当系统运动到18.2 mrad时,系统沿θx和θy轴运动的带宽分别骤降为47.92 Hz和57.1 Hz。
综上所述,当采用常值陷波滤波器时,系统在不同位置处的带宽性能会有巨大的差异,因而无法保证FSM系统在大行程运动时的带宽性能。其原因在于:当FSM系统的运动位置增大时,其刚度增大,从而导致共振频率随之变大。此时,常值陷波滤波器已无法很好地消除共振模态的影响。
表3 采用常值陷波滤波器时不同位置处FSM的带宽
Tab.3 Bandwidth of FSM at different positions using fixed notch filter
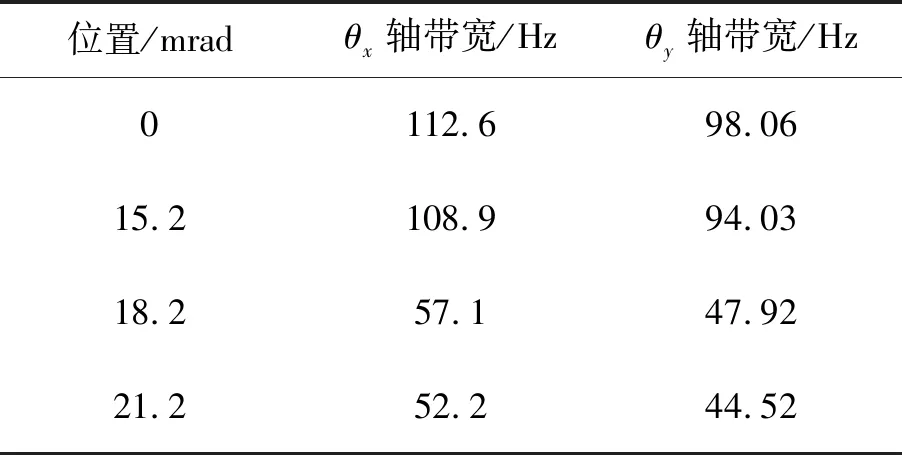
位置/mradθx轴带宽/Hzθy轴带宽/Hz0112.698.0615.2108.994.0318.257.147.9221.252.244.52
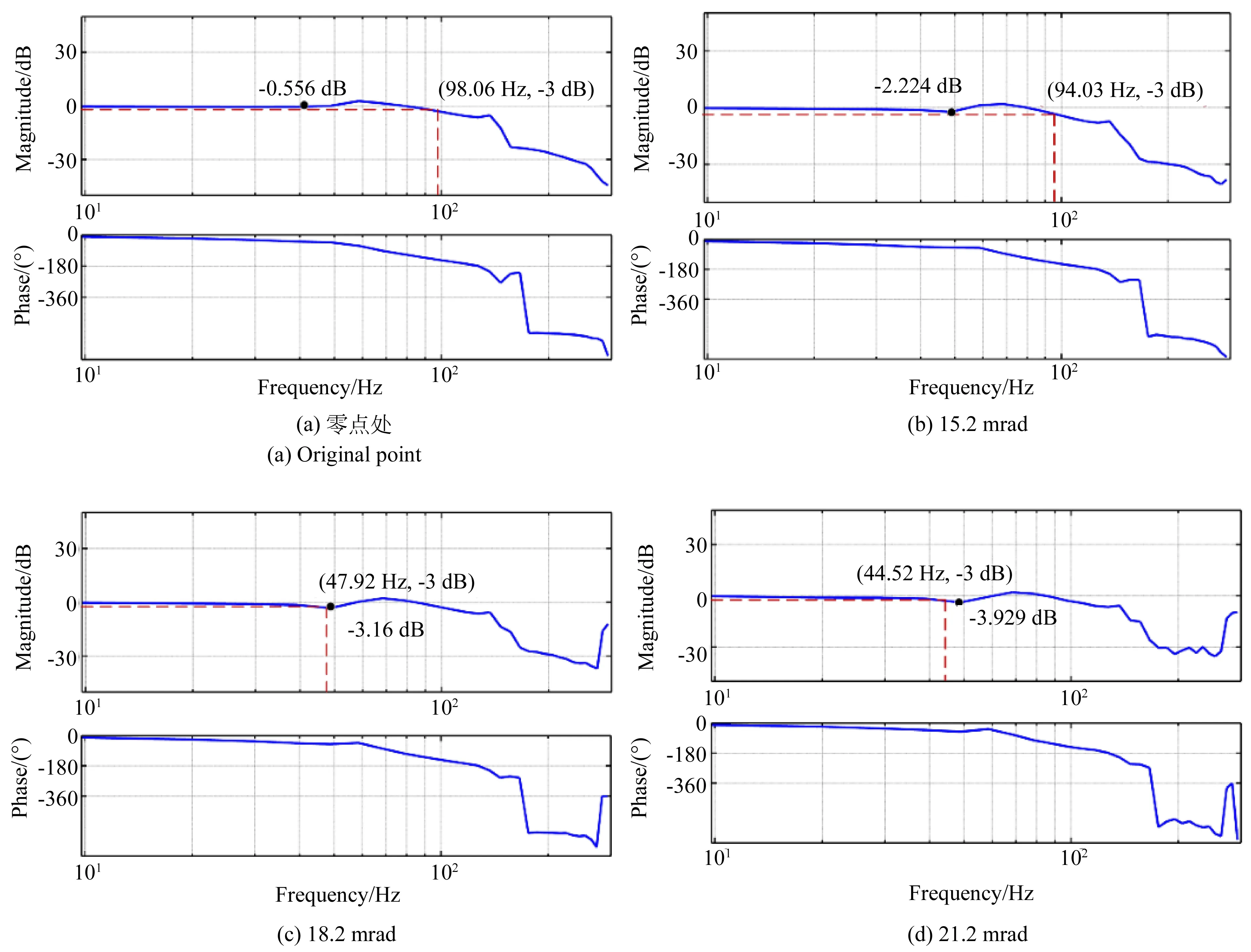
图8 采用常值陷波滤波器时θx轴在不同位置处的带宽

图9 采用常值陷波滤波器时θy轴在不同位置处的带宽
6.2 变值陷波滤波器
在不同位置处,对FSM系统进行辨识,得到其共振频率与运动位置的关系为:
ωx=13.85x2-2.82x+337.67.
(18)
对于变值陷波滤波器,由于其共振频率随着运动位置的变化而变化,在Simulink中直接采用“Transfer Fun”将它写为传递函数的方式无法实现。在本文中,变值陷波滤波器的实现方法如图 10所示。
首先将式(8)所示的陷波滤波器的传递函数改写为状态变量,即为:
(19)
其中:x1,x2代表状态变量,y和u分别代表输出和输入。
然后,在Simulink中调用“S-Function Builder”,根据式(18)和式(19),模块“Outputs”中的程序可表示为:
“double w;
w=13.85*pow(u2[0],2)-2.82*u2[0]+337.67;
y0[0]=(2*0.07747*w-2*w)*xC[1]+u1[0];”
模块“Continuous Derivatives”中的程序可表示为:
“doublew;
w=13.85*pow(u2[0],2)-2.82*u2[0]+337.67;
dx[0]=xC[1];
dx[1]=-pow(w,2)*xC[0]-2*w*xC[1]+u1[0]。”
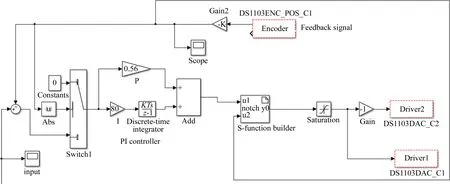
图10 变值陷波滤波器Simulink 软件程序
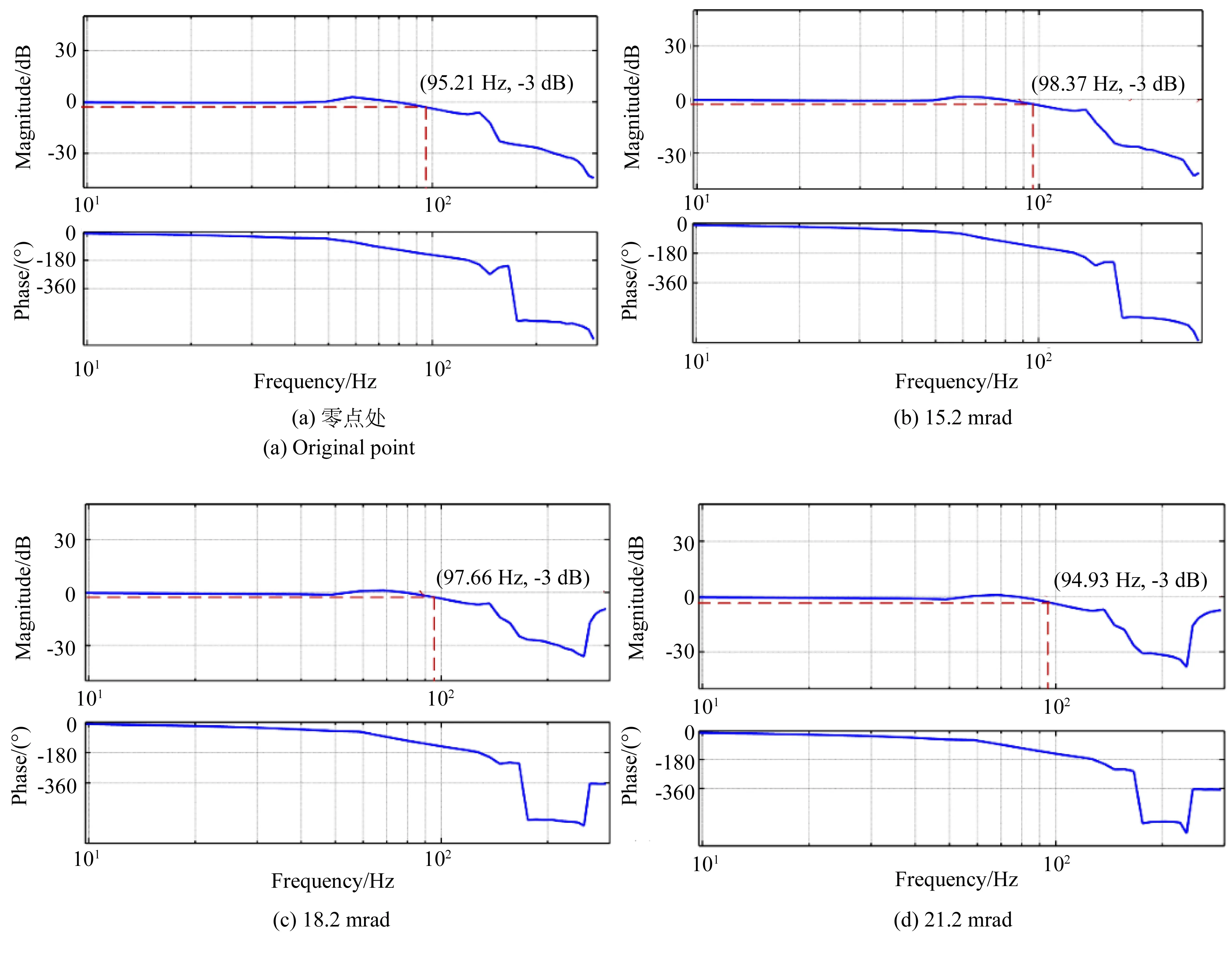
图11 采用变值陷波滤波器时θx轴在不同位置处的带宽
通过实验测试了θx轴采用变值陷波滤波器时FSM在不同位置处的带宽性能,如图 11所示。同理可得到θy轴在不同位置处的带宽性能,如图 12所示。

图12 采用变值陷波滤波器时θy轴在不同位置处的带宽
根据实验结果可知,随着运动位置的增大,FSM系统在共振频率点附近处的频率响应基本平稳,并未出现明显的衰减。如表4所示,系统沿θx和θy轴运动时的闭环带宽基本稳定在95 Hz和110 Hz。
表4 采用变值陷波滤波器时不同位置处FSM的带宽
Tab.4 Bandwidth of FSM at different positions using variable notch filter

位置/mradθx轴带宽/Hzθy轴带宽/Hz0112.695.2115.2111.898.3718.2109.897.6621.2107.494.93
通过对FSM平台输入阶梯信号来测试其最小分辨率,如图13所示,FSM平台的最小分辨率为±0.03 mrad。
综上所述,采用变值滤波器可以有效地消除FSM系统随位置变化而改变的共振模态的影响,使系统的带宽性能在各个位置保持稳定。通过实验验证了变值滤波器的有效性和必要性。
7 结 论
本文针对基于音圈电机驱动的FSM在大行程运动时电机动子和定子发生碰撞的问题,设计了新型的FSM柔性机构来消除电机动子的横向位移。针对FSM在大行程运动时的共振频率会随运动位置的变化而改变的问题,设计了变值陷波滤波器来保证系统在不同位置处的带宽性能保持一致。设计的变值陷波滤波器的共振频率为FSM运动位置的函数,并结合PI控制器实现闭环控制。实验结果表明:采用常值陷波滤波器时,系统在不同位置处的带宽差异较大;当系统的运动位置小于15.2 mrad时,FSM沿θx和θy轴的带宽分别为95 Hz和110 Hz左右;当系统运动到18.2 mrad时,θx和θy轴的带宽分别骤降为47.92 Hz和57.1 Hz。采用变值陷波滤波器时,快反镜沿θx和θy轴在不同位置处的带宽基本稳定在95 Hz和110 Hz,验证了变值陷波滤波器的有效性。

