冰蓄冷空调负荷预测的预估校正模型

李壮举，柴 帅，栾 茹

(北京建筑大学 电气与信息工程学院，北京 100044)

0 引 言

为了鼓励“移峰填谷”重要措施，冰蓄冷技术在中国得到迅速发展。但现行大多数的冰蓄冷空调系统都根据工作人员的经验来判断运行，空调系统运行费用保持在较高的状态。如何根据建筑负荷需求，制定优化运行策略是必须要解决的问题，而精准地预测冷负荷是其前提。

刘庆典等[1]利用时间序列实现对空调的逐时负荷预测。徐笑强[2]采用BP神经网络对逐时空调负荷进行预测，成功计算出了经济最优的冷量分配结果。王蕾等[3]通过利用改进的神经网络对中央空调冷负荷进行逐时预测，预测精度较高。

总结现有的负荷预测方法可知，一般人工神经网络的能够达到较高的精度，但在实时性和泛化能力方面尚需提高；时间序列的模型精度显得不足；支持向量机可以依靠少数关键样本进行收敛，提高了建模的快速性，但模型精度不高，而且对于大量样本数据进行训练时，却需要大量资源和时间，其模型无法在线使用。所以，探寻新的收敛速度更快、泛化能力更强的负荷预测方法，势在必行。为了提高冰蓄冷空调系统的精度和稳定性，在现有的基础上，提出采用小波神经网络构建负荷预测预估模型，并采用direct HDP实时更新预估模型参数，提高了冷负荷预测精度。

1 小波神经网络模型的建立

1.1 小波神经网络的确定

冰蓄冷系统控制的影响因素可以分为外部干扰和内部干扰。外部干扰包括太阳辐射、干湿度等等，内部干扰包括人员负荷、设备散热等。正是由于冰蓄冷空调系统是受这些因素影响的非线性系统，必须要找到合适的方法，捕捉其影响因素与预测冷负荷之间的相关线性或非线性关系,得出空调负荷的周期特性和随机变化规律，而前馈神经网络可以通过自学习并采用较少的隐层节点实现拟合。

小波神经网络(wavelet neural network，WNN)[4]是基于具有良好的聚焦特性和时域局部特性的小波变换与具有自适应、自学习、鲁棒性、推广能力的神经网络结合起来构建的模型，即用线性小波基函数取代神经网络结构中隐含层节点的传递函数。小波神经网络可以通过调节其平移因子和伸缩因子，将信号分解为低频分量和高频分量，较BP神经网络其网络结构更简单，收敛速度更快，同时可以避免BP神经网络等结构设计上的盲目性，有更强的泛化能力，较时间序列分析法有更高的预测精度。为了实现更高精度的预测，本文采用WNN来实现冰蓄冷空调的冷负荷预测，其小波神经网络拓扑结构如图1所示。

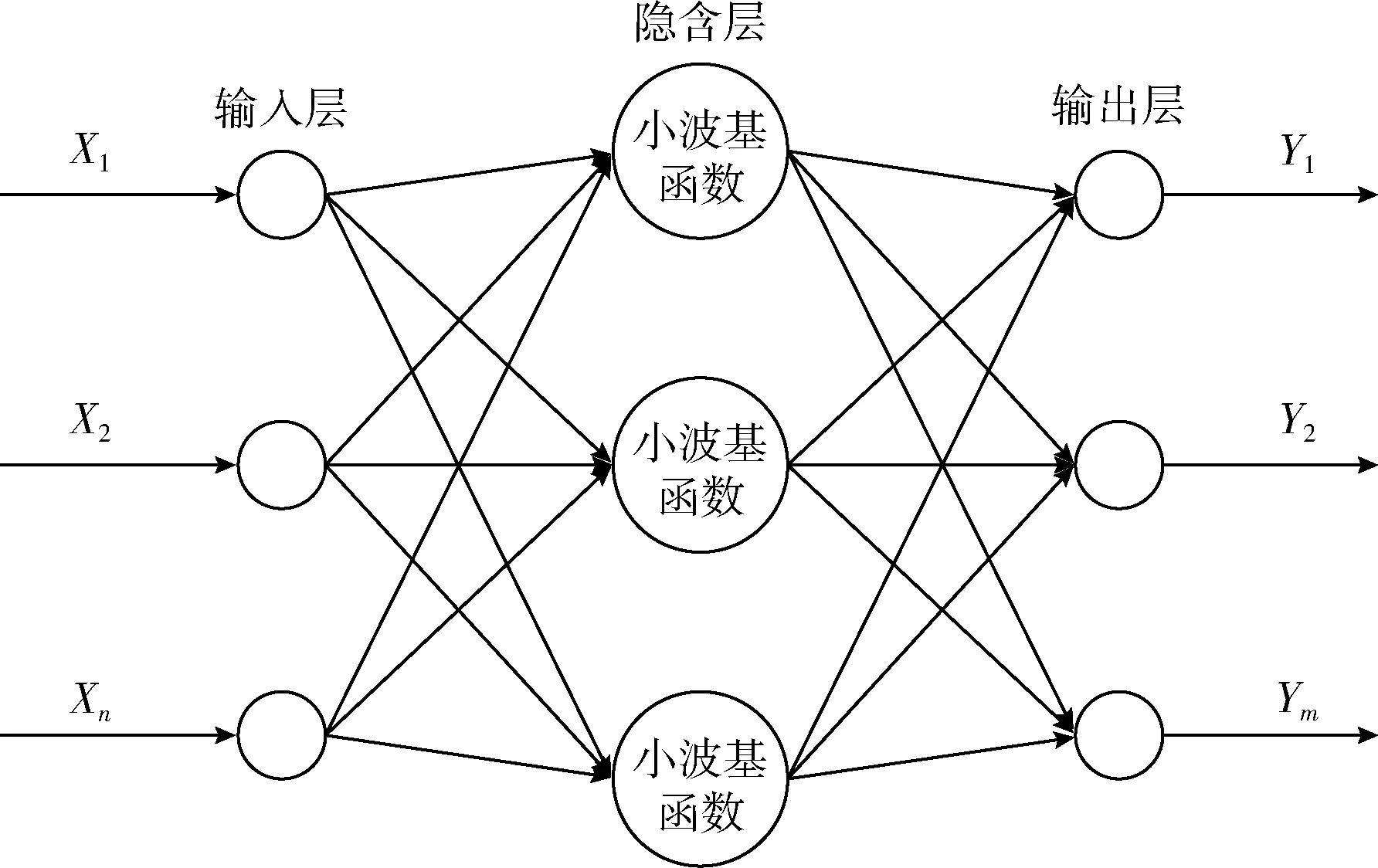
图1 小波神经网络拓扑结构

1.2 利用小波神经网络实现冰蓄冷空调负荷预测的算法

小波神经网络是利用小波基函数作为BP神经网络隐含层的传递函数，其中小波变换的定义请参见文献[5]。根据小波神经网络拓扑结构，其隐含层输出为

(1)

其中，xi为输入值，wij为输入层与隐含层的权重；f(j)为隐含层第j个节点输出值；aj为小波基函数的伸缩因子；bj为小波基函数fj的平移因子

(2)

式中：γ一般取1.75。

1.3 网络结构

1.3.1 输入与输出参数的选择

对于大型的冰蓄冷空调系统，影响参数非常多。根据建筑冷热负荷计算DOE-2标准规定[6]，在计算冷负荷时提供了14种参数，包括室外干球温度、室外湿球温度、相对湿度、大气压、云态、云量、室外空气焓、风速、风向、水平太阳辐射强度、散射太阳辐射强度、地面散射辐射强度、降雪和降雨量等。根据输入参数对于冰蓄冷空调冷负荷影响程度的重要性，通过ARIMA的方法[7]，确定选用神经网络输入层神经元7组主要影响参数为：时刻、室内人员负荷、室外干球温度、室外相对湿度、水平太阳辐射强度、t-1时刻的系统冷负荷，t-24时刻的系统冷负荷，而输出层的参数为t时刻系统冷负荷。

1.3.2 网络结构的确定

当输入层与输出层确定，需要确定隐层数与隐层节点数。根据Kolmogorov定理[8]可知，对于非线性与大滞后的网络结构，使用三层结构的神经网络就可以解决，所以确定冰蓄冷空调负荷预测模型为三层神经网络模型。

隐含层节点数对于模型性能的优良具有举足轻重的作用。对于隐层节点数的选取，有一个相关经验公式[9]，公式如下

(3)

(4)

其中，k是训练样本的总数量，n是输入层节点数；l是输出层节点数，m是隐含层节点数，α是取值为1到10的常数。通过式(3)与式(4)得出隐含层节点个数的取值范围为4到14，通过试凑法，考虑神经网络的误差与泛化能力，得出当隐含层神经元个数取11时，神经网络综合效果最佳，具体实验结果见表1。

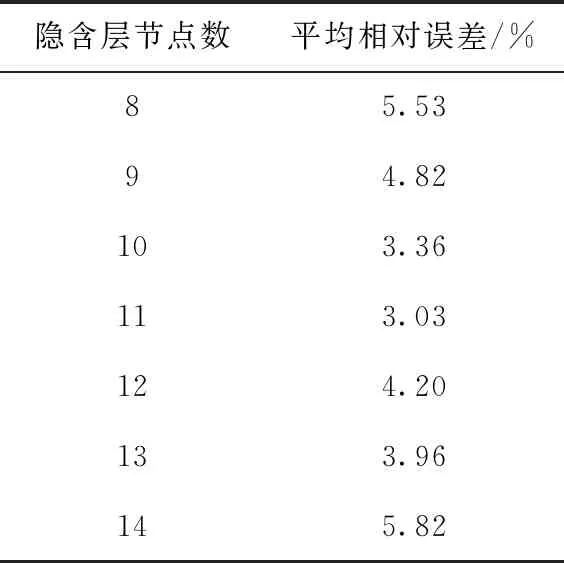
表1 部分采集样本数据

所以确定建立三层神经网络模型，其中输入层节点数为7个，隐含层节点数为11个，输出层节点数为1个。

2 基于direct HDP的负荷预测校正模型

冰蓄冷空调预测的影响因素具有多变性和随机性。系统在一定时间内，外部环境实时发生变化，这就需要预测的模型能够根据外部环境的变化及时更新结构参数和网络权值等特性调节变量，实现自适应。即需要一种方法能够通过学习输入数据，实现对网络模型结构参数和网络权值等变量的控制。为了实现更高精度的预测，采用动态规划理论，在逐时的冰蓄冷空调负荷预测模型中增加了校正环节。

动态规划理论是一种解决多阶段过程最优化问题的数学方法，其定义请参见文献[10]。而其中的自适应动态规划(adaptive dynamic programming，ADP)[11]正好能解决这个问题。直接启发式动态规划(direct heuristic dynamic programming，direct HDP)[12]作为ADP体系的一个重要分支，优点就在于能够在不依赖于实际对象模型的基础上实现在线学习。并且根据实时数据对神经网络的性能指标参数进行优化，自动调整预测参数，使其实现更优的线性逼近能力，以达到实时预测。因此，确定选用direct HDP用来在线学习实现校正环节。direct HDP原理图如图2所示。

图2 direct HDP拓扑结构

如图2所示，执行网络(actor neural network，ANN)和评价网络(critic neural network，CNN)作为其主结构，α为折扣因子，取值范围是0到1之间，是衡量不同时刻的差距因素对预测目标的影响指标；r(t)是不同时段的代价函数；u(t)是用来调节变量的增减量，是用于修正预估环节参数的控制量；J(t)为其代价函数。由此可知，为了实现整个预估校正模型，使用小波神经网络实现direct HDP中的执行网络，并使用BP网络来实现其中的评价网络。

direct HDP方法中评价网络的优化目标为

(5)

最优解的可以通过迭代等方式获得，公式如下

(6)

为了满足Bellman最优性方程，通过评价网络预估代价函数J，使误差函数Ec(t)的最小化对评价网络的训练，以到达预测值与真实值的逼近

(7)

ec(t)=αJ(t)-[J(t-1)-r(t)]

(8)

关于评价网络权值调整采用梯度下降法进行训练

(9)

其中，lc(t)为评价网络在t时刻的学习率，wc(t)为评价网络的权值系数。

最优控制u是用执行网络进行预估的，即对其网络模型参数变量的预估，以使代价函数达到最优。为了对执行网络的进行训练，使用误差函数Ea(t)最小化的处理方式，公式如下

(10)

ea(t)=J(t)-Uc(t)

(11)

式中：Uc(t)为J(t)的目标值。

通过优化代价函数，使ANN能够最小化CNN的输出。更新算法采用梯度下降法

(12)

式中：la(t)为执行网络的学习率，wa(t)为执行网络的权值系数。

3 预估校正模型建立的流程

冰蓄冷空调负荷预测的预估校正模型建立的流程步骤：

(1)对数据进行标准归一化处理，归一于0～1；

(3)设置输入层、隐含层和输出层节点个数；

(4)确定网络学习率lr1和lr2,最大迭代次数Nd以及目标误差e；

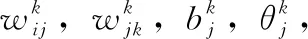
其中预估环节为步骤(1)到步骤(6)，校正环节为步骤(7)到步骤(9)。

基于小波神经网络的冰蓄冷空调负荷预测并附加direct HDP 的模型结构如图3所示。

图3 预估校正模型结构

4 实验结果及分析

本实验采用MATLAB R2014a作为实验平台，以杭州某冰蓄冷空调工程为研究对象，该系统采用常用的主机位于上游的串联蓄冷形式，将2018年6月5日至2018年8月8日共计1560小时采集到的数据作为训练样本集，来预测2018年8月9日至2018年8月13日共计120小时的冷负荷数据，部分实测冷负荷如图4所示。

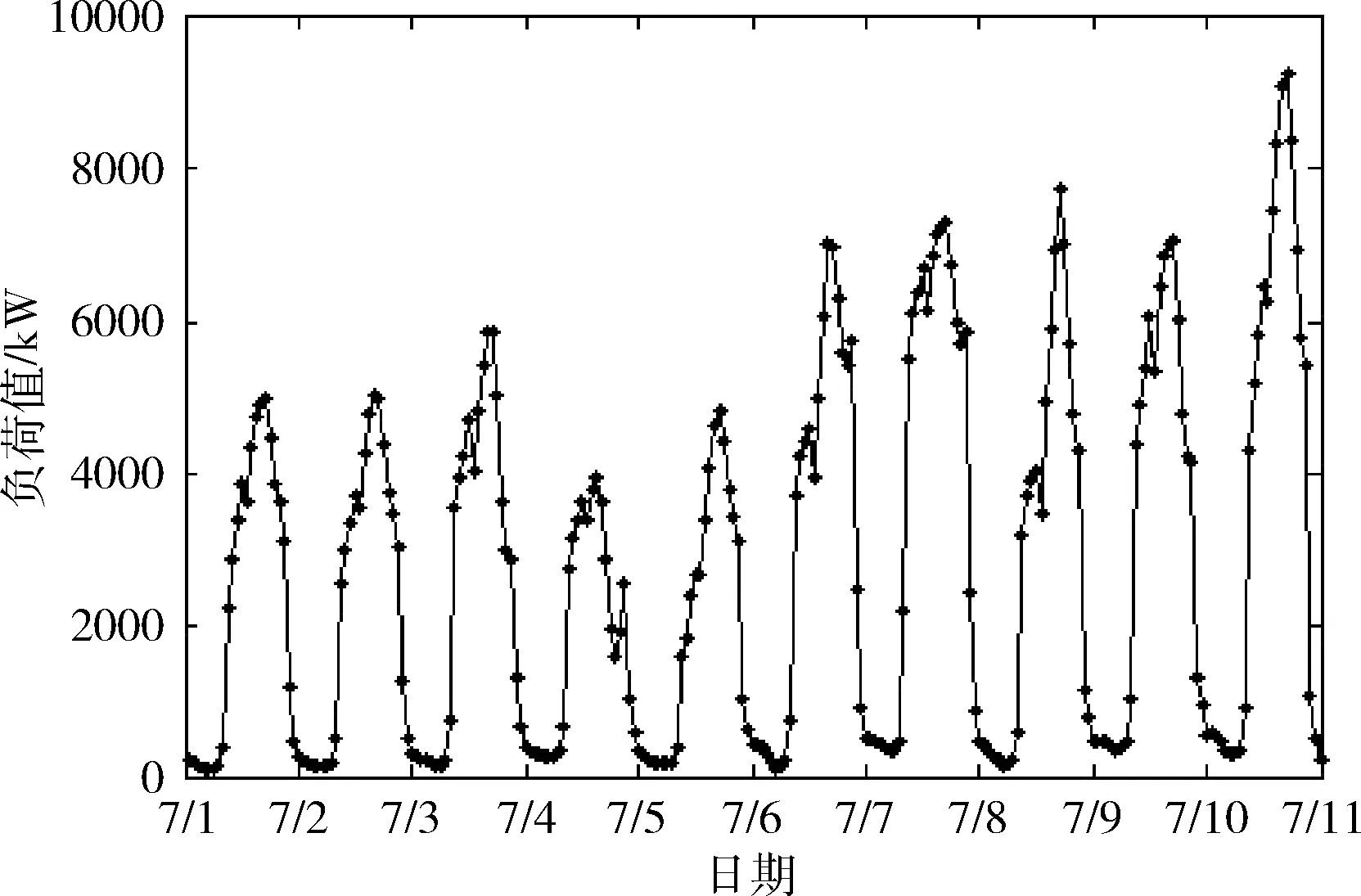
图4 部分实测冷负荷

通过观察发现，在工作日的冷负荷较非工作日的冷负荷大得多，工作日一般都会在下午1到3点达到供冷高峰期，部分采集样本数据见表2。

本文分别采用两种方法建立神经网络模型：小波神经网络预测，在小波神经网络预测的基础上增加direct HDP来进行优化校正，其中小波神经网络预测方法是采用文献[4]的方法对冰蓄冷空调进行负荷预测。网络结构参数设定如下：最长训练时间设置为5000 Epochs,目标误差为10-5,学习率lr1为0.01，lr2为0.001。

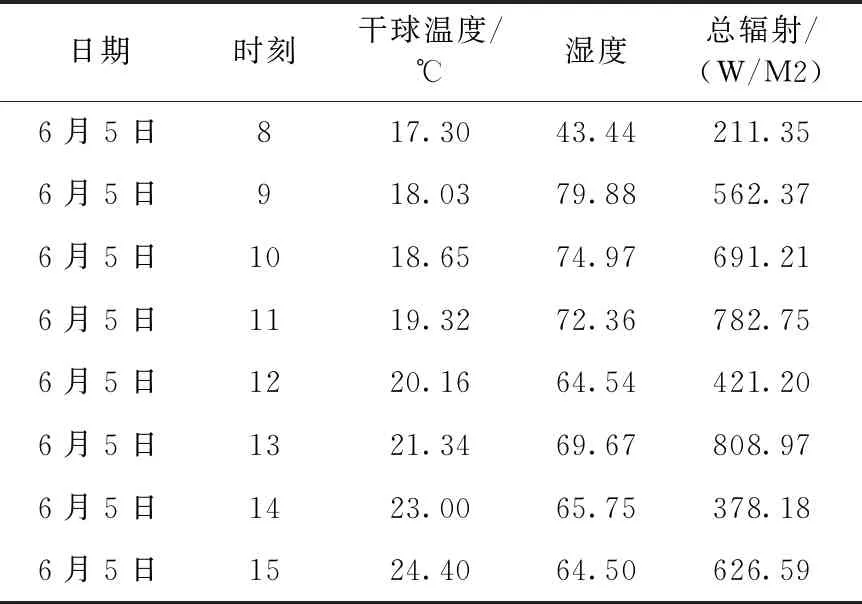
表2 部分采集样本数据

为了防止出现对原始序列的纯时间滞后效应，在离线训练预估模型时对训练序列增加了带限的白噪声信号，以使得网络具有良好的泛化能力，其预测结果如图5所示。

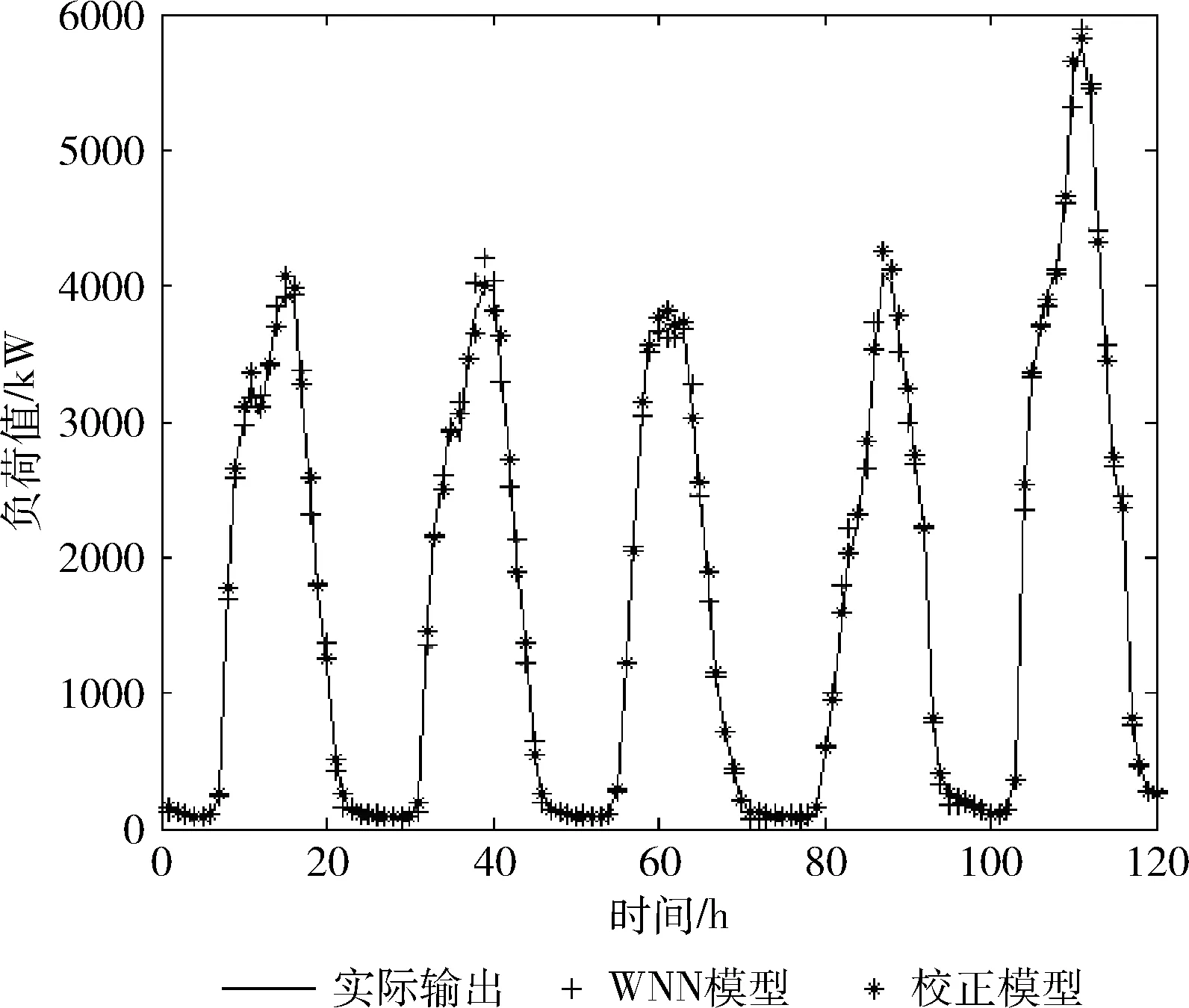
图5 负荷预测结果对比

如图5所示，两种方法对冰蓄冷空调负荷预测均有不错的预测结果。为了进一步对两种方法预测进行分析，利用相对误差图与绝对误差图对比的预测精度差异。如图6和图7为两种方法预测值与实际值的绝对误差图和相对误差。

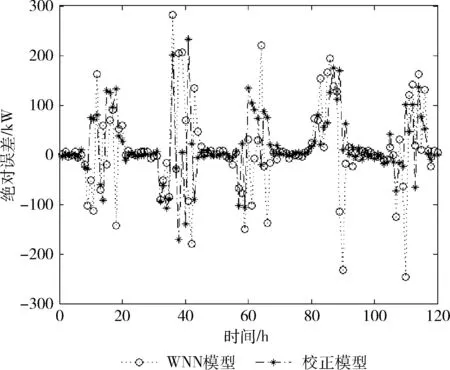
图6 预测值与实际值的绝对误差

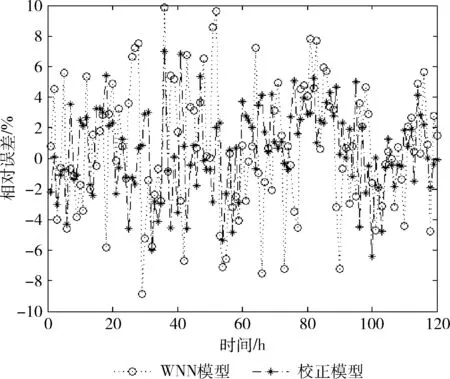
图7 预测值与实际值的相对误差

如图6所示，校正后的输出和WNN模型输出的预测误差最大值都在300 KW以下，这主要是由于小波变换能够通过表征信号局部特征，对预测值进行降噪，减小了神经网络预测精度的大幅波动。

通过图7可知，在供冷低峰期的相对误差相对于高峰期的相对误差普遍更大，这主要是由于供冷高峰期与供冷低峰期差值太大，而且供冷低峰期负荷绝对值比较小，致使相对误差值比较大。由于direct HDP优化能实时获取数据，校正模型能够及时更新最优模型参数，使校正模型在供冷高峰期预测相对误差减小，趋于稳定，提高预测精度。通过表3的数据可以更直观地分析两种方法模型的评价指标。

表3 预测结果分析

通过以上实验，采用direct HDP优化结构的校正模型对冰蓄冷空调系统进行负荷预测相对于小波神经网络预测模型各种评价指标都有所提升，平均绝对值相对误差提高了1.02%，平均绝对误差减低至41.50 kW·h，并使均方根误差降低至66.22 kW·h。

5 结束语

本文提出基于小波神经网络的冰蓄冷空调负荷预测技术，并通过构建direct HDP附加优化结构对预估模型进行校正，通过实际工程进行了仿真。通过实验对比，小波神经网络的方法可以避免因外部和内部因素变化导致存在的误差对预测模型的扰动。在增加校正环节后，因direct HDP优化结构具有自适应学习能力，通过采集实时数据，调节最优神经网络模型参数，提高了冰蓄冷空调负荷预测的精度。如何根据冷负荷和电费因素，采用最优控制方式，算出最优日运行费用是下一步研究重点。