自适应多策略花朵授粉算法
瞿博阳,李国森,焦岳超,柴旭朝,闫 李
(中原工学院 电子信息学院,河南 郑州 450007)
0 引 言
花朵授粉算法(flower pollination algorithm,FPA)鲁棒性好、实现简单和计算速度快,已在实际生活和工程领域中得到成功应用[1-7]。然而,FPA算法极易陷入局部最优解且寻优精度不高。另外FPA的有关研究相当欠缺,如何提升其性能具有一定的研究意义。
针对FPA存在的不足,国内外学者在改进其寻优性能方面展开了研究。其中,一些学者采用增强多样性的策略提高全局寻优能力。李前等[8]使用莱维飞行以提高寻优速度。崔丽群等[9]将折射原理引入花朵授粉算法,以跳出局部最优。Zhou等[10]采用精英反向策略以平衡勘探和开采能力。王玉鑫等[11]使用均匀变异策略,以改善种群的探索能力。El-Shahat等[12]采用杂交策略提高种群多样性。乔现伟等[13]使用混沌序列提升算法的寻优效率。另外,通过结合其它算法也能求解到很好的结果。肖辉辉等[14]融合引力搜索算法,以改善花朵授粉算法的搜索效率。Nabil等[15]将克隆选择算法引入花朵授粉算法,以改善种群多样性。Wang等[16]融合人工蜂群算法,以提高算法的全局勘探能力。
为进一步改善FPA的不足,本文提出自适应多策略花朵授粉算法(SMFPA),该算法采用锚点策略以提高种群的多样性;使用摄动策略以改善全局勘探能力;利用局部搜索策略以加强局部寻优能力。
1 花朵授粉算法
花朵授粉算法包含两个操作:全局授粉、局部授粉,并依赖转换概率p(p=0.8)进行授粉方式的选择。其主要思想:先初始花粉种群,然后依据转换概率p选择其中的一个操作进行位置更新,不断重复此过程直至条件终止[17]。

(1)


(2)
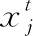
2 自适应多策略花朵授粉算法
2.1 锚点策略
在传统花朵授粉算法中,每个花粉在全局授粉过程中采用全局最优信息进行位置的更新,这很难保持种群的多样性。
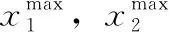

图1 锚点策略
为此,在全局授粉过程中,式(1)更新定义如下
(3)
2.2 摄动策略
如果花粉个体在连续若干代内总是访问同一个锚点,那么在下一次迭代,该花粉个体仍有很高的概率访问该锚点,这将导致花粉个体过度探索某一锚点所在的区域,而难以寻找更优的解。因此,摄动策略的基本思想是对这样的花粉个体进行一定的摄动,使该花粉个体选择新的锚点。首先为第i个花粉定义一个摄动因子ζi, 其更新规则如下
(4)
式中:at,at-1分别是当前和前一次迭代中第i个花粉所访问的锚点。如果连续两代,花粉个体总是访问同一锚点,则花粉个体i的摄动因子ζi增加1。
如果ζi>ζmean, 那么第i个花粉将进行摄动,即按式(5) 进行更新
(5)
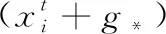
2.3 局部搜索增强策略
在标准FPA算法中,局部授粉采用随机选择两个花粉的方式来实现花粉位置更新,导致寻优过程具有盲目性。因此,式(2)重新定义如下
(6)
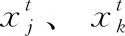
2.4 SMFPA的实现步骤
步骤1 设置SMFPA的参数:花粉种群规模NP,测试函数维数n,转换概率p等。
步骤2 根据佳点集原理构造锚点,并计算适应度值,初始种群等于锚点,每个锚点中的最优解等于其本身,每个花粉的摄动因子初始化为0。
步骤3 对于每个锚点,计算种群中离其最近的个体,比较该个体和其锚点中解的适应度。若个体优于锚点中的解(a*),则替换,否则,保持锚点中解不变。
步骤4 找出种群全局最优(g*)。
步骤5 依据式(4)更新每个花粉的摄动因子。
步骤6 判断是否满足 (p>rand)。 若满足,则依据式(3)执行全局授粉操作。
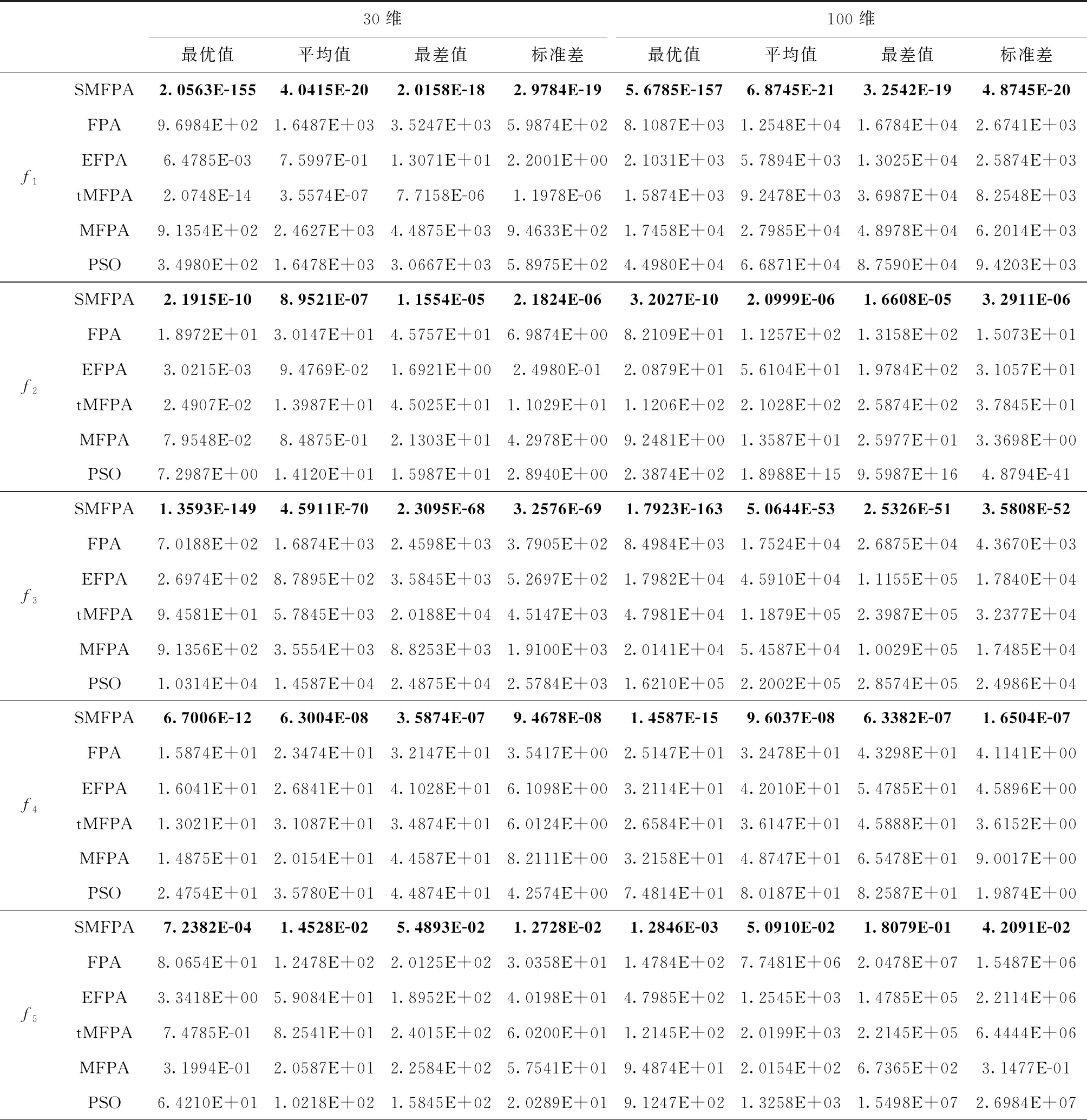
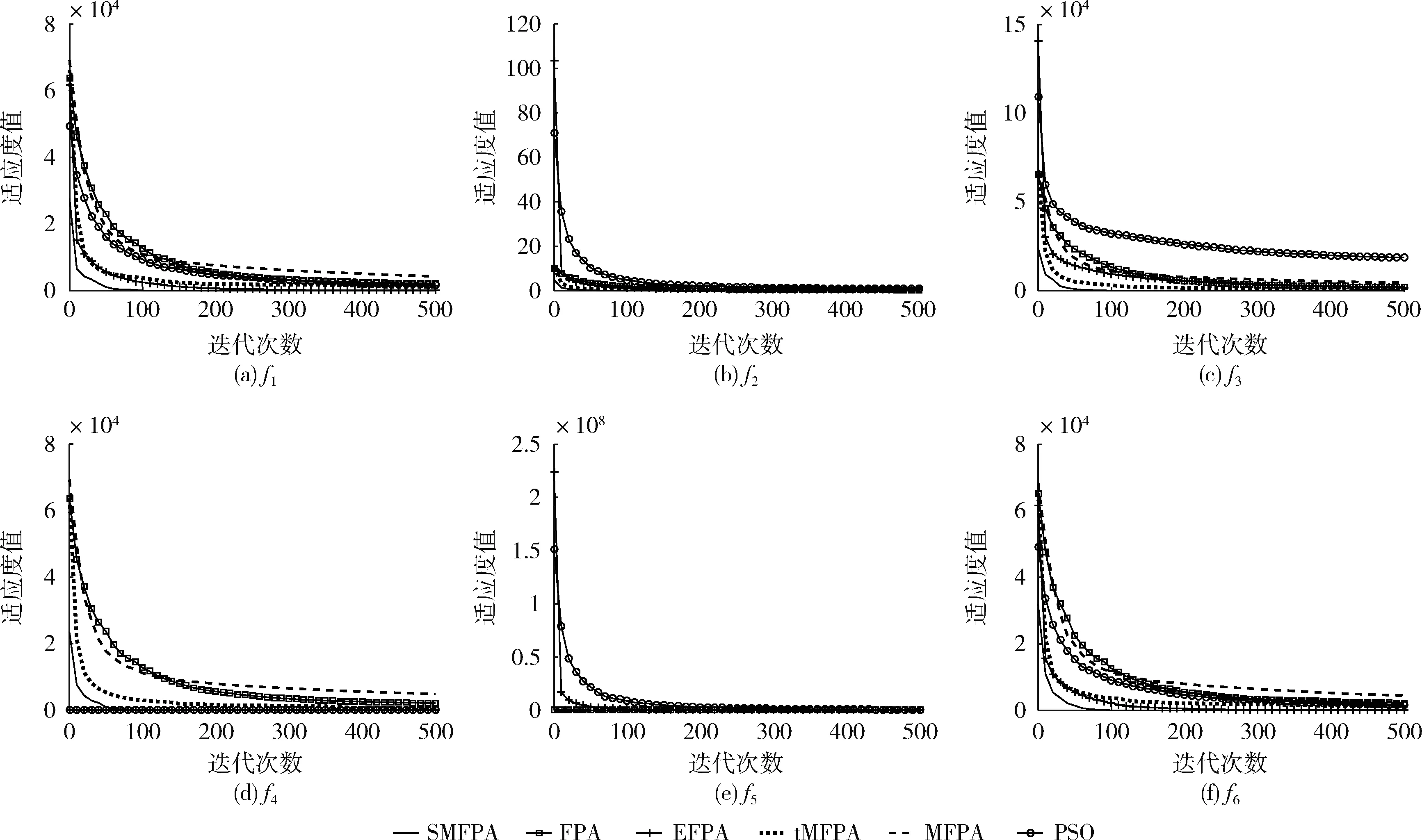
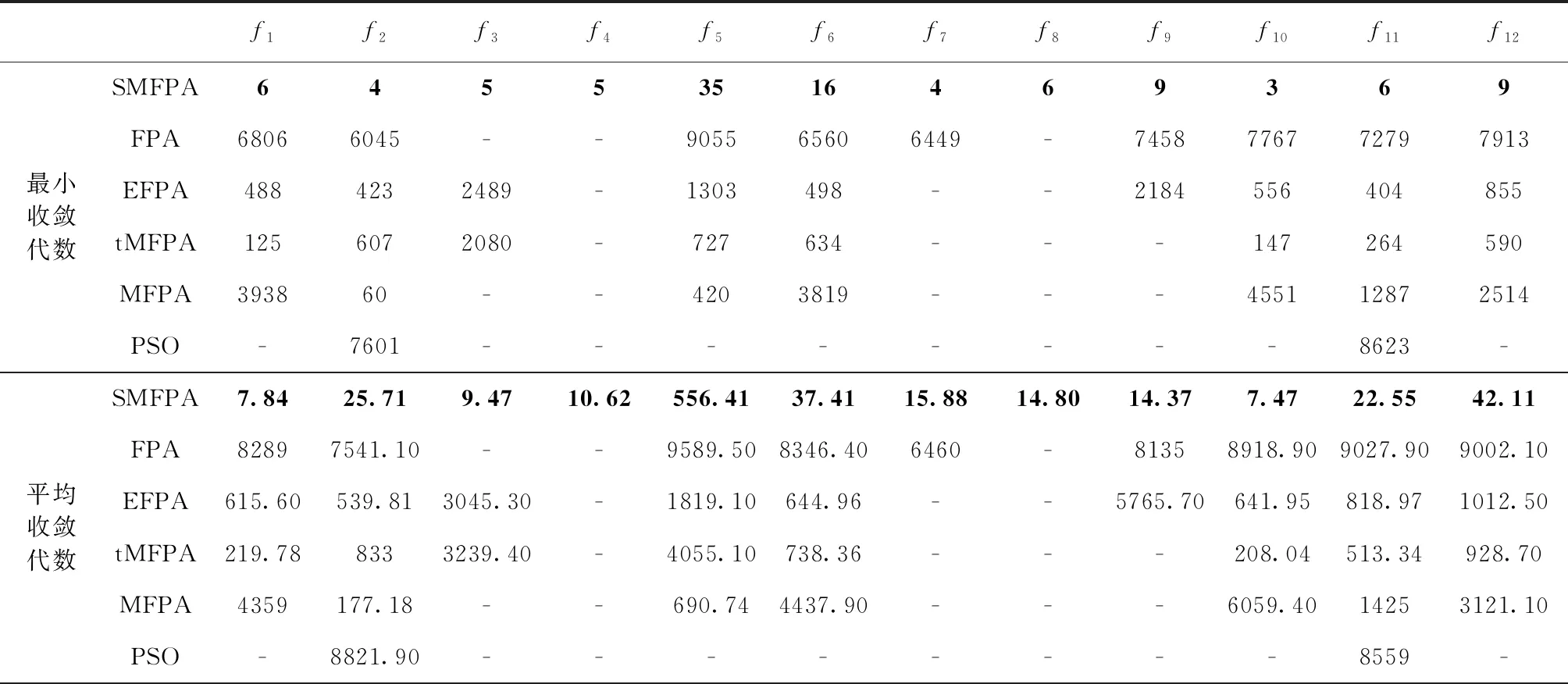
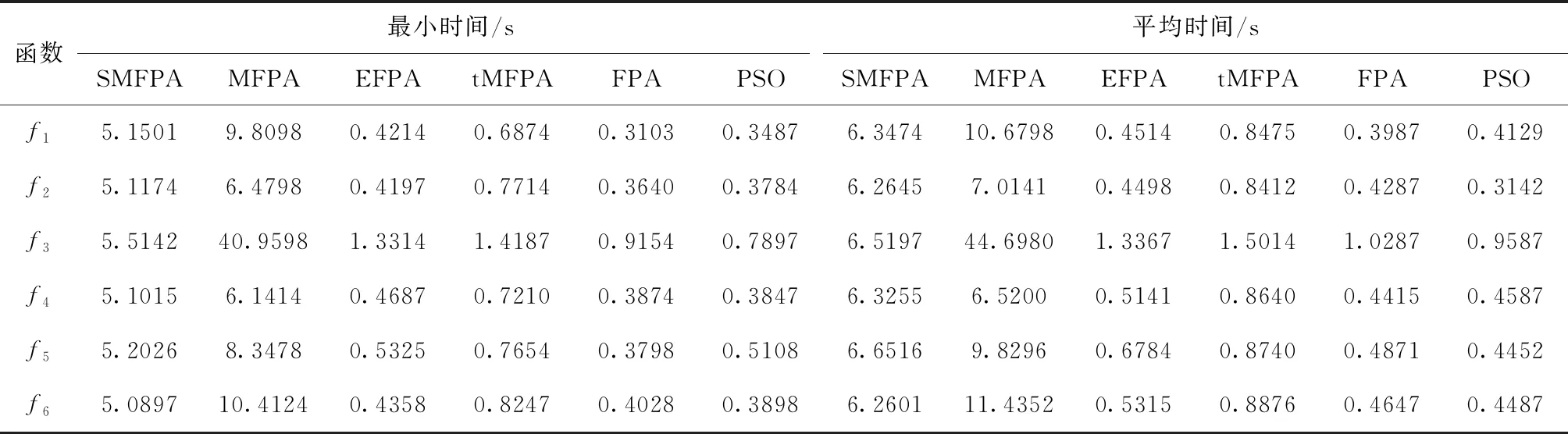
步骤7 判断是否满足 (p 步骤8 判断是否满足 (ζi>ζmean)。 若满足,则按照公式(5)对花粉进行摄动策略。 步骤9 求出当前最优解,并更新对应的适应度值。 步骤10 判断是否满足实验设置的最大迭代次数。若满足,输出最优花粉位置及其适应度值并终止程序,否则执行步骤3。 为了测试SMFPA算法的性能,选择12个测试问题进行不同算法的对比[22,23]。其函数表达式等信息见表1。其中,f1~f7为单模问题,用于评估对比算法的寻优精度。f8~f12为多模问题,具有多极值的特点[24]。因此,该类函数更难求解。 表1 基准测试函数 将SMFPA与其它5种算法(FPA[1]、tMFPA[11]、MFPA[15]、EFPA[25]、PSO[26])进行对比。其中,算法种群规模NP是30。其它对比算法的参数保持与相应文献一致。 3.3.1 固定迭代次数的性能分析 通过固定迭代次数,比较算法的最优值、平均值、最差值及标准差。实验设置:算法独立运行30次;问题维度为30和100;最大迭代次数为500。结果见表2。 在30维和100维情况下,SMFPA算法的最优值、平均值、最差值小于其它几种算法,收敛精度相对高于其它算法,而且标准差最小,算法的搜索结果最稳定,具有良好的鲁棒性。对于函数f8和f10,SMFPA算法能够收敛到理论最优值。而且SMFPA算法在多模问题f8~f12表现良好,避免陷入了局部值,求解到了最优解。而其它算法的性能较差,收敛缓慢,主要体现在其最优值、平均值、最差值较大,甚至难以收敛到最优值。这表明SMFPA采用锚点策略、摄动策略、局部搜索增强策略不同程度的改善了勘探和开采能力。为直观比较算法收敛性能,图2为6个测试函数(f1~f6,30维)的适应度值进化曲线。 表2 固定迭代次数下不同算法结果对比(30维和100维) 表2(续) 图2 函数进化曲线 在同一迭代次数下,SMFPA算法达到的适应度值小于其它算法;在相同的适应度值下,SMFPA算法达到的迭代次数小于其它算法。另外,SMFPA算法在100次迭代后基本能够找到最优解,而其它算法所需的迭代次数更多。总体上,SMFPA算法的寻优性能更好。 3.3.2 固定收敛精度下的性能分析 通过固定收敛精度,比较算法的收敛性(最小收敛代数、平均收敛代数及收敛率)。实验设置:算法独立运行30次;收敛精度目标为0.01;问题维度为30;最大迭代次数为10 000。在表3中,最小收敛代数表示算法优化到收敛精度目标的最小进化代数;平均收敛代数表示算法优化到收敛精度目标所需代数的平均值;收敛率表示算法优化到收敛精度目标的运行次数/总独立运行次数;“-”表示算法迭代次数超过最大迭代次数仍未达到收敛精度目标。从实验结果可知,SMFPA算法的最小收敛代数、平均收敛代数及收敛率均优于其它算法。而其它算法优化到收敛精度目标所需的迭代次数较大,甚至无法收敛最优解。总体上,SMFPA的收敛速度更快。 表3 固定精度下不同算法结果对比 表3(续) 3.3.3 时间复杂度分析 以函数f1~f6为例,比较算法在时间复杂度上的可行性,实验参数设置与3.3.1节相同。从表4可知,PSO和FPA所需时间最短。其次是EFPA,tMFPA和SMFPA。对于FPA,时间复杂度:O(NP);对于SMFPA,包含3个策略,分别为锚点策略、摄动策略和局部搜索增强策略,各策略的时间复杂度:T(FPA基本操作)=O(NP);T(锚点策略)=O(NP*NP);T(摄动策略)=O(NP);T(局部搜索增强策略)=O(NP)。 因此,T(SMFPA)=T(FPA基本操作)+T(锚点策略)+T(摄动策略)+T(局部搜索增强策略), 化简后可以得到SMFPA算法的时间复杂度为O(NP*NP)。 相比FPA算法,SMFPA复杂度有所提高。总体上,SMFPA算法的时间复杂度相对较低。 表4 算法运行时间对比 为验证SMFPA算法的性能,对管柱设计问题进行了计算。管柱设计问题是在满足约束g1,g2条件下,求解管柱直径d和厚度t使其成本最小[27]。Yang[27]、Hsu[28]、Rao[29]采用不同的算法对其进行求解。表5展示了SMFPA算法和其它算法的结果对比。可以看出,和其它算法相比,SMFPA算法的求解结果更优。 表5 不同算法结果对比 本文提出自适应多策略花朵授粉算法(SMFPA),采用锚点策略使种群个体充分利用邻域信息以改善算法收敛速度,提高花粉个体多样性;利用摄动策略对过度开采某一区域的花粉个体进行摄动以防止陷入局部极值,改善全局勘探能力;采用局部搜索增强策略使种群寻优更具有方向性并提升开采最优解的能力。对比算法在12个测试函数和管柱设计问题上的寻优结果表明,SMFPA算法在寻优速度以及寻优精度方面表现更好。3 实验结果与分析
3.1 测试函数的选择

3.2 实验参数设置与方法
3.3 结果与分析


4 工程应用

5 结束语

