单位圆盘上凸调和函数的系数条件与拟共性延拓

江苏南京理工大学理学院 杨佳霖 张 珣 邱郑宜人

一、绪论

有关调和函数的更多细节，我们可以查阅参考文献[8]，[9]和专著[2]。

则函数f ∈H 是α 阶的凸调和函数（见[9]）。我们记CH（α）为α 阶凸调和函数组成调和函数类。

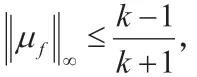
当f 是调和 的 时候，通过(1.2)，Avci 和Zlotkiewicz([1])利用系数an，bn给出了f 成为星象函数的一个充分条件，Silverman([10])给出了当b1=0 时，f 是单叶的、保向的和星象的充分条件。Jahangiri ([6])推广了当b1不一定为0时的相应结果。Hamada等（[5]）给出了使f 可以拟共性延拓到整个复平面的一个充分条件。

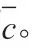
二、α 阶凸的充分系数条件

在本节中，对于f ∈H，我们将证明关于f ∈CH（α）以下充分条件。

那么f 在单位圆盘Δ 内是单叶调和函数，且f ∈CH（α）。

证明 首先我们证明f 是局部单叶的且在单位圆盘△内保向，这是因为

在下文中，我们验证f 是单叶的。如果g（z）=0，则f 是解析的，并且其单叶性遵循其凸性（[3]）。如果g（z）≠0，我们现在证明当z1≠z2时，f（z1）≠f（z2）。

对于单位圆盘Δ 内的z1≠z2，我们得到z（t）=（1-t）z1+t z2∈Δ，其中0 ≤t ≤1。因此可以写成：

另一方面，通过(2.1)

联合(2.2)和（2.3），我们可以得到f 是单叶的。

下面证明f ∈CH（α）。根据(1.3)，我们只需要证明

其中，z=reiθ，0 ≤θ＜2π，0 ≤r＜1, and 0 ≤α＜1。

不难验证Rew ≥α 当且仅当|1-α+w|≥|1+α-w|，因此我们只需证明|A(z)+（1-α）B(z)|-|A(z)-（1+α）B(z)|≥0，

通过(1.2)中h 和g 的系列展开，我们得到了

将(2.5)、(2.6)与条件(2.1)、(2.4)相结合，得到

证明完毕。

三、调和函数的拟共形和拟共形延拓

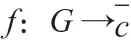
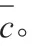
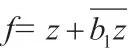
由于f 不是仿射映射，通过(2.1)，易知

结论2 f 在单位圆盘Δ 上是绝对连续的。

对于任意z1，z2∈Δ，且z1≠z2，有

这意味着f 在单位圆盘Δ 上是绝对连续的。

在[5]中证明了以下定理：

定理3的证明 根据定理A，为证明定理3，我们只需要验证（2.1）是否满足定理A 中的条件。

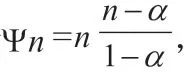
对于任意n ≥3，且

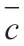
证明完毕。