考虑状态相关服务的城市交叉口离散事件仿真建模

齐 心，胡 路，赵 斌，唐晓佩

考虑状态相关服务的城市交叉口离散事件仿真建模

齐 心1，胡 路2,3，赵 斌2,3，唐晓佩2,3

（1. 天津市市政工程设计研究院，天津 300051；2. 西南交通大学，交通运输与物流学院，成都 611756；3. 综合交通大数据应用技术国家工程实验室，成都 611756）

准确模拟交叉口处车辆运行, 对交叉口信号配时优化、交叉口设计等具有重要意义。交叉口排队建模可以较为准确地模拟车辆到达及交叉口服务过程。位相型分布（PH分布）, 可以无限逼近任意到达和服务规律, 车辆到达交叉口时交叉口处容量有限, 且车辆通过交叉口时, 通过时间具有状态相关性。本文考虑以上三点, 建立PH/PH（）/1/2的交叉口排队模型, 将城市交叉口抽象为离散事件仿真模型, 根据PH分布随机变量计算车辆到达过程和交叉口服务过程。文中提出的离散仿真模型充分考虑了车道服务的状态相关性，并利用Simulink构建了考虑状态相关服务的城市交叉口离散事件仿真模型。仿真结果表明考虑状态相关服务的离散事件仿真, 可以较好地反映出交叉口处车辆通过的周期性, 较为客观地反映交叉口车辆运行情况。

交通工程；离散仿真；排队系统；城市交叉口；PH分布

0 引 言

合理的城市交叉口信号控制优化可以有效减少车辆延误时间和停车次数，增加交叉口通行能力，保障车辆安全有序运行。因此，对城市交叉口进行研究，准确便捷地仿真模拟车辆到达和通过交叉口的行为，对交叉口信号相位配时优化、交叉口设计等具有重要意义。

目前常见的建模仿真方法有离散事件仿真和微观仿真。其中，微观仿真建模一般可以较为详细地描述个体的特征和行为，因此需要更为广泛的校准工作和更大的计算时间[1]。而离散事件仿真建模（DES）不需要特定的物理环境和实体，相较微观仿真而言更为有效和更易校准，且具有普遍性和高效性[2]。现有很多研究都进行过对城市交通中的行人及车辆的仿真。早在1970年，Clifford[3]便曾为城市轨道交通车站的规划和设计建立了乘客仿真模型；Hoogendo[4]利用微观仿真模型，对车站客流进行了仿真研究；胡路[5]利用离散事件仿真建立城市轨道交通车站的PH（）/PH（）/1/2的排队网络模型。

车辆在交叉口处运行时，由于前后车和信号相位配时的影响，在与交叉口相连的路段、交叉口进口道及交叉口出口道处均出现排队现象，故可将交叉口视为排队网络。在排队模型中，合适的车辆到达和交叉口服务的分布函数的选取对模型的准确性影响较大。PH分布具有在理论上可以无限逼近任意到达和服务规律的特性，可从理论上解决“一般到达”信号交叉口车流的排队建模，为信号配时优化提供更为真实的车流描述[6]。车辆在路段及交叉口中运行时，其运行速度与路段当前状态下的车辆数有关，即车辆在排队系统中接受服务的服务率是状态相关的。因此，本文提出考虑车辆到达及交叉口服务服从PH分布，交叉口服务率为状态相关的离散事件仿真模型PH/PH（）/1/2。

1 交叉口排队网络系统描述

1.1 排队系统及PH分布

排队系统是指具有排队等待现象的服务系统。排队系统根据服务台个数、排队形式的不同，可以分为单队列单服务台、单队列多服务台以及多队列多服务台排队系统。多服务台排队系统根据服务台的连接形式不同也可以分为并联、串联及混联排队系统[7]。

PH分布，也称位相型分布，是一个有限状态Markov过程吸收时间的分布，它具有良好的通用性、解析特性和可计算性，在理论上可以无限逼近任意到达规律和服务规律，在相当大的程度上保持了指数分布的解析运算性质且具有良好的封闭性。

由于车辆到达时间间隔和服务时间均为连续型随机变量，在此仅讨论连续型PH分布。当一个非负随机变量服从连续型PH分布时，其分布函数可表达为：

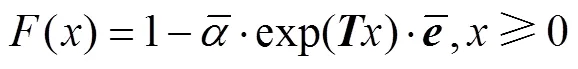
1.2 信号交叉口排队系统描述

在建立信号交叉口排队系统模型之前，对交叉口各类排队系统组成部分进行合理描述。

城市道路中的交叉口是一种开放的排队系统。在开放的排队网络中，车辆从外部进入与交叉口相连的路段，进行排队及服务，再由路段进入交叉口进口道中，在进口道中接受服务，再进入交叉口出口道，在交叉口出口道中再次接受服务后离开交叉口排队系统。由于路段、交叉口进口道、交叉口出口道均为无明显服务台的设施，车辆在路段、交叉口进口道、交叉口出口道的排队系统均可理解为无明显服务台设施的排队系统。信号交叉口排队系统主要由与交叉口相连路段排队系统、进口道排队系统、出口道排队系统三部分构成，如图1所示。

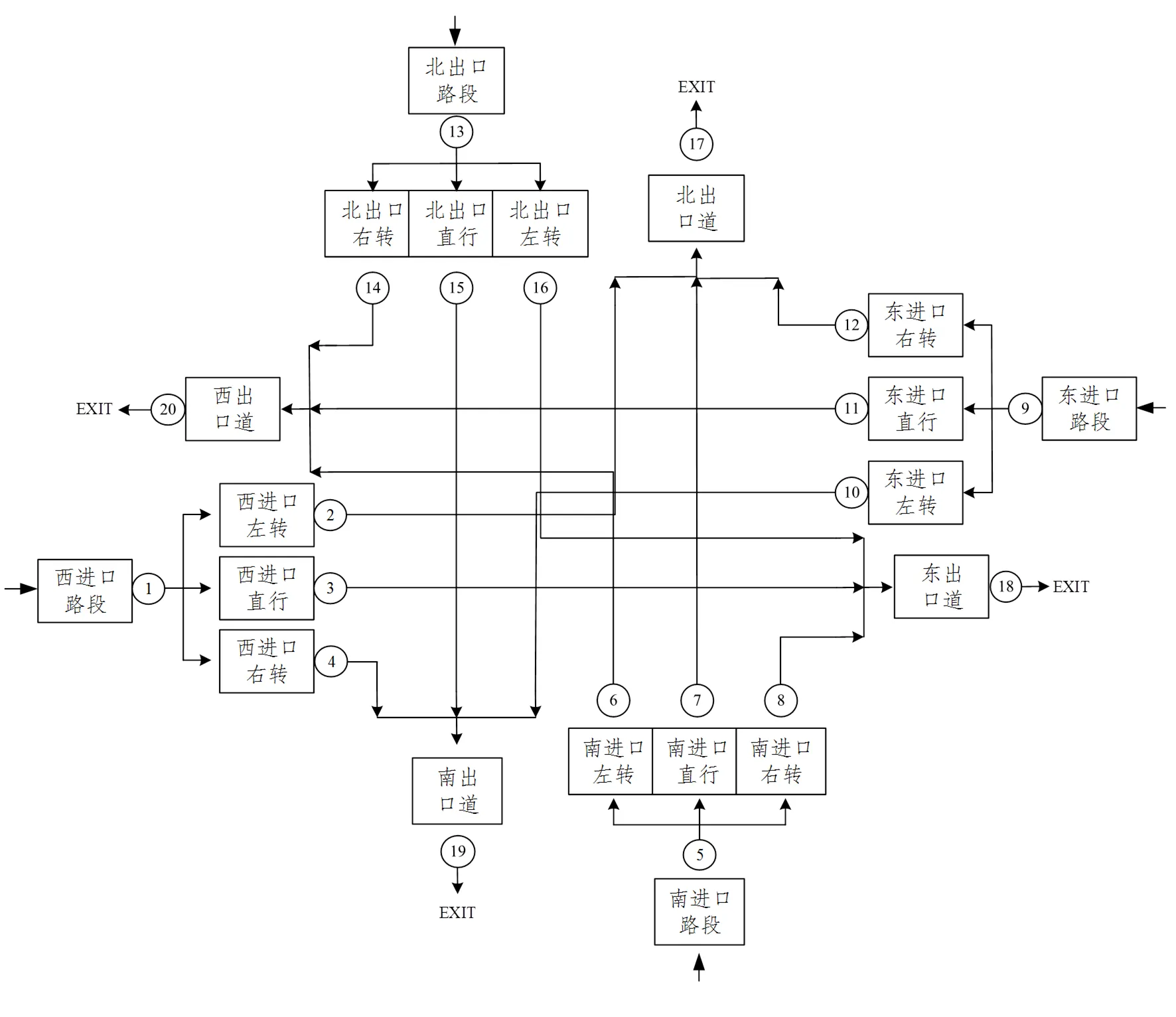
图1 城市交叉口排队网络拓扑图

根据Smith等人[9]的研究，车道上每个可占用的位置均可视为一个服务台，即服务台数量和系统容量相等。交叉口排队系统可视为多服务台混联排队系统。车辆按照一定时间间隔分布A到达路段，当路段内部车辆数（系统状态）增加时，车辆速度的平均值逐渐降低，随着路段中车辆的数目增加或者减少，车辆通过路段的过程为状态相关的，即车辆在路段的服务时间是状态相关的。同理，车辆在交叉口进口道和出口道运行的服务时间也是状态相关的。因此，车辆通过交叉口可抽象为一个车辆到达服从分布A，具有1个混联服务台，车辆总服务时间服从B()的，系统容量为2的排队系统，即A/B()/1/2的混联排队系统。

当排队系统具有1个混联服务台时，1的取值可能会上百。过大的服务台数量使得仿真模型较难搭建，因此考虑将排队系统进行简化[7]。考虑用一个虚拟的单服务台代替1个混联服务台。当车辆连续通过虚拟服务台时，将前一辆车离开虚拟服务台的时间作为后一辆车开始被服务的时间。此时，具有1个混联服务台的排队系统A/B()/1/2可等效转换为具有单个服务台的排队系统A/B’()/1/2，其中B()B()。

将车辆在路段、交叉口进口道、交叉口出口道的运行过程抽象为构建排队系统，如图2所示。

图2 交叉口排队系统改造

1.3 交叉口排队系统构建

交叉口排队系统主要包括与交叉口相连路段排队系统、交叉口进口道排队系统、交叉口出口道排队系统，主要包含了车辆到达过程、车辆排队过程、服务过程、车辆分流合流过程及车辆消失过程。下面对几个过程分别进行描述和构建：

1.3.1 车辆到达过程

交叉口的车辆到达主要体现在与交叉口相连路段的车辆到达，车辆到达服从一定的规律。每个时间段车辆的到达服从一定的统计规律。路段排队系统的输入流仅有一个部分，来自于前一段路段。

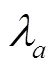
车辆平均到达率为单位时间内到达车辆数，可由调研数据统计获得。

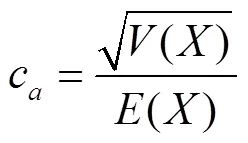
1.3.2 车辆排队

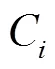
式中：l为车道的长度；1为平均车辆长度，一般取值为4m；2为最小车距，一般取值为1m。

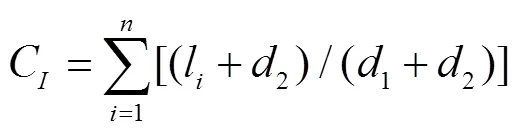
式中：为交叉口进口道数或路段车道数。

1.3.3 交叉口分流合流过程

交叉口车辆分流过程即为车辆在交叉口进口道前按照左转、直行、右转进入不同进口道的过程。在将交叉口构建为排队系统后，交叉口分流应按照一定的转向比进行。

1.3.4 交叉口服务过程

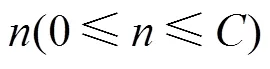
在交叉口进口道中，若仅有一条车道，则可视为多服务台串联排队系统，若存在多个同方向车道，则可视为混联多服务台排队系统，车道之间为并联，同一个车道不同位置之间为串联，其服务时间为状态相关。为简化模型，本文将多个混联服务台及串联服务台抽象为虚拟服务台，将串联/混联多服务台排队系统抽象为单服务台排队系统，服务台的服务时间受系统内车辆数的影响，为状态相关的服务过程。

对于进口道而言，服务率是单位时间通过交叉口的车辆数，服务率的倒数为车辆离开交叉口的时间间隔，即单虚拟服务台的状态相关的服务时间。单虚拟服务台状态相关的服务时间可表示为：

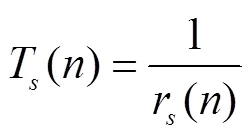
交叉口系统的服务率可通过平均速度进行计算：

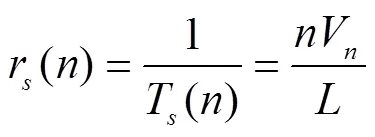
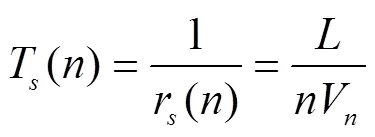
为计算状态相关服务的服务率，需对状态相关速度模型进行分析。

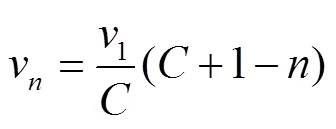
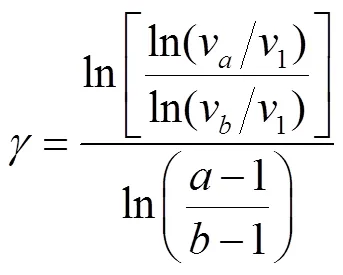
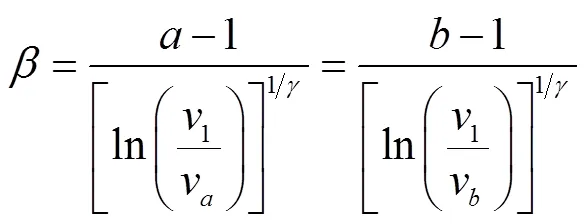
根据Smith[12-14]等的研究，不同交通流特征点的取值如表1所示。表中，为车道长度，为车道宽度。

表1 三个交通流特征点的取值

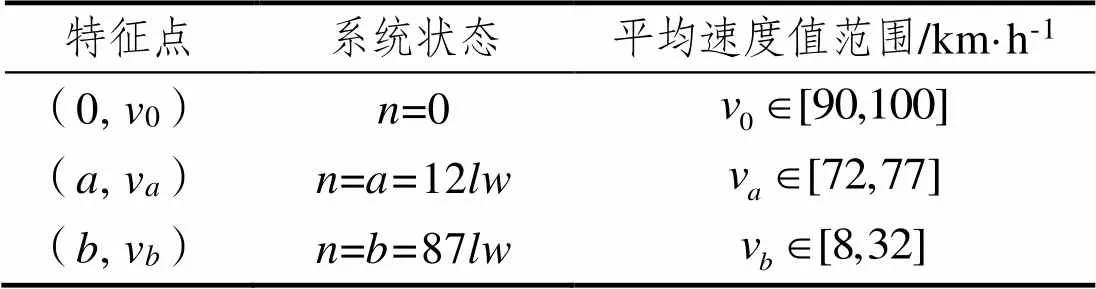
Tab.1 Value ranges of three representative points

考虑实际现象，在路段极为拥挤时，车辆在路段运行的平均速度降低但不会为0；其运行时间有所增加，但不会趋近于无穷。因此，指数模型与现实情况的吻合度较高。

因此，多服务台转化为单虚拟服务台后，其服务率应为：

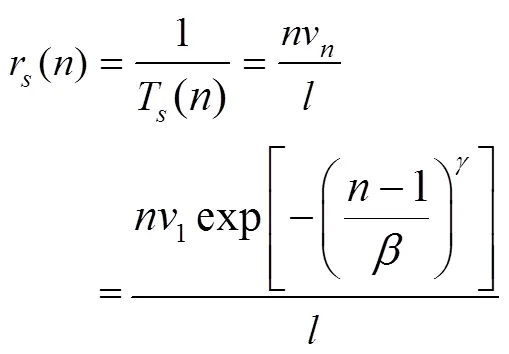
1.3.5 车辆消失过程

在车辆进入交叉口出口道完成服务后，车辆紧接着进入路段继续运行，在仿真中，由于仅考虑车辆在交叉口的运行状态，因此车辆在完成交叉口出口道的运行后，会在系统中消失。

2 离散事件仿真模型建立

2.1 离散事件仿真模型概述

本节提出交叉口排队系统的离散事件仿真建模。城市交叉口是一种通道设施，可以利用离散事件仿真的方法进行分析、建模和仿真。利用离散事件仿真建模，可以快速地建立城市交叉口的仿真模型。

2.1.1 离散事件仿真

离散事件仿真（DES）是指对系统状态在离散时间点上发生变化的系统所进行的仿真，其事件的发生无论在时间上还是空间上都是离散的，一般以某种顺序发生，或者在某种条件下发生，事件的发生大多具有随机性，状态变化也是发生在离散时间点上的。离散事件建模仿真中，主要包括实体、实体属性、活动、状态、事件、进程、队列等组成部分。

2.1.2 SimEvents

SimEvents是由MathWork开发的离散事件仿真建模的工具，它嵌入Matlab中，用于离散事件系统建模及仿真，扩展了Simulink动态系统仿真环境，实现了使用队列和服务的概念完成离散事件系统的仿真。通过SimEvents可以便捷的创建离散事件仿真模型，可以仿真整个系统中实体数据在系统中各个部分中的传递流程，实现基于事件模拟实体通过队列、服务器、门等的传递[15]。此外，SimEvents还可以结合Simulink，实现连续事件系统、离散事件系统以及离散事件系统的仿真。SimEvents提供了离散事件仿真平台和相关模块集，主要有发生模块、输出模块、服务器模块、队列模块、时钟模块、路径选择模块及S-函数模块等。通过这些模块的组合应用，便可以实现利用SimEvents进行离散事件仿真建模。

选择SimEvents进行城市交叉口离散事件仿真建模的原因有三个：（1）SimEvents和matlab的紧密结合有助于后续的结果处理和仿真优化；（2）SimEvents由于允许使用强大的模块集，便于创建不同运输设施的排队模型，较为适用于运输系统的建模；（3）利用SimEvents进行离散事件仿真建模更易修改。

2.2 城市交叉口离散事件仿真建模

在SimEvents中建立一个城市交叉口离散事件仿真模型，如图3、图4所示。

2.2.1 车辆生成

在PH/PH（）/1/2的离散事件仿真模型中，车辆在路段处生成。根据1.3.1中分析，车辆到达系统的过程服从PH分布，因此，利用PH分布完成车辆的生成。

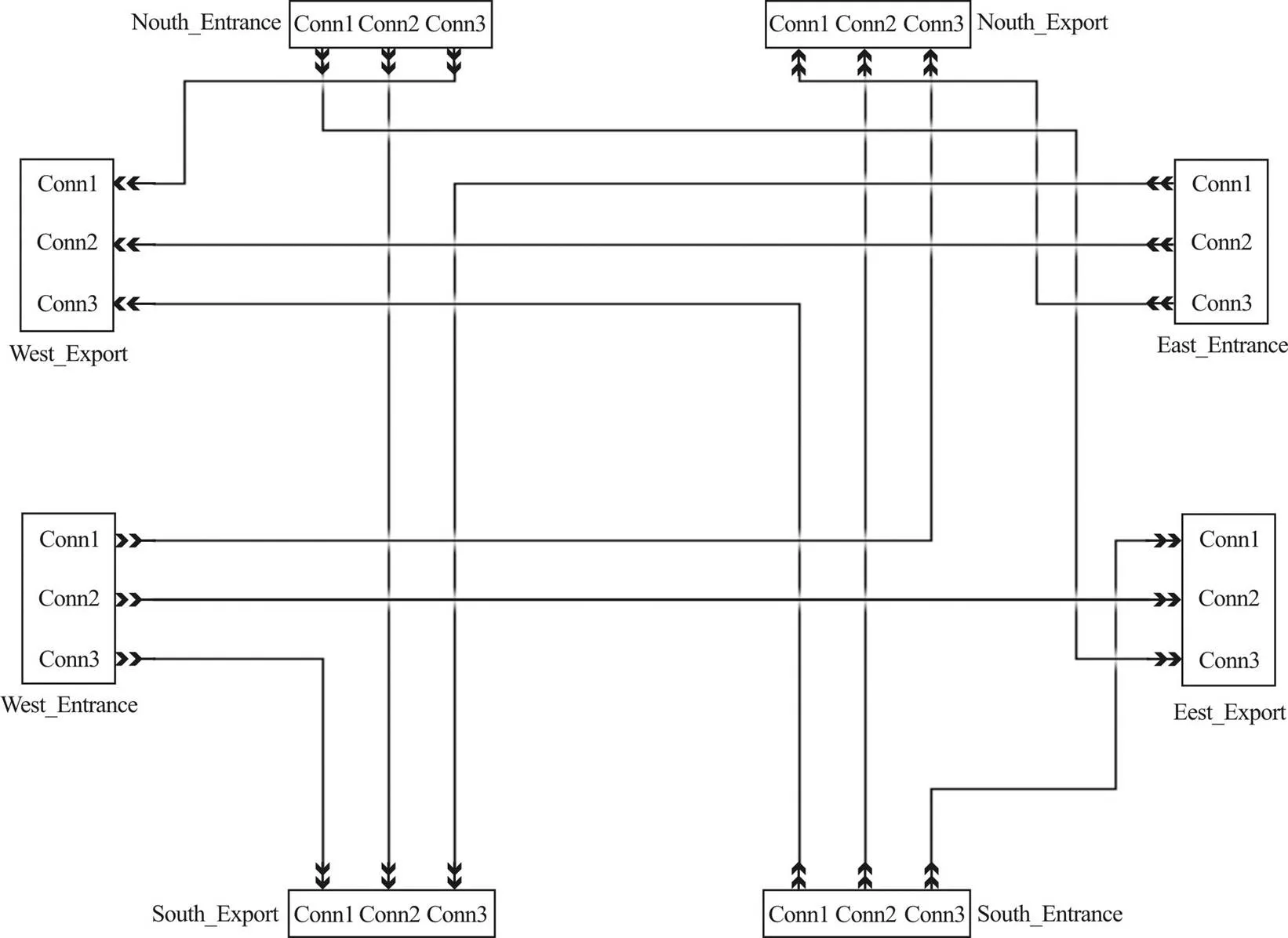
图3 交叉口离散事件仿真模型

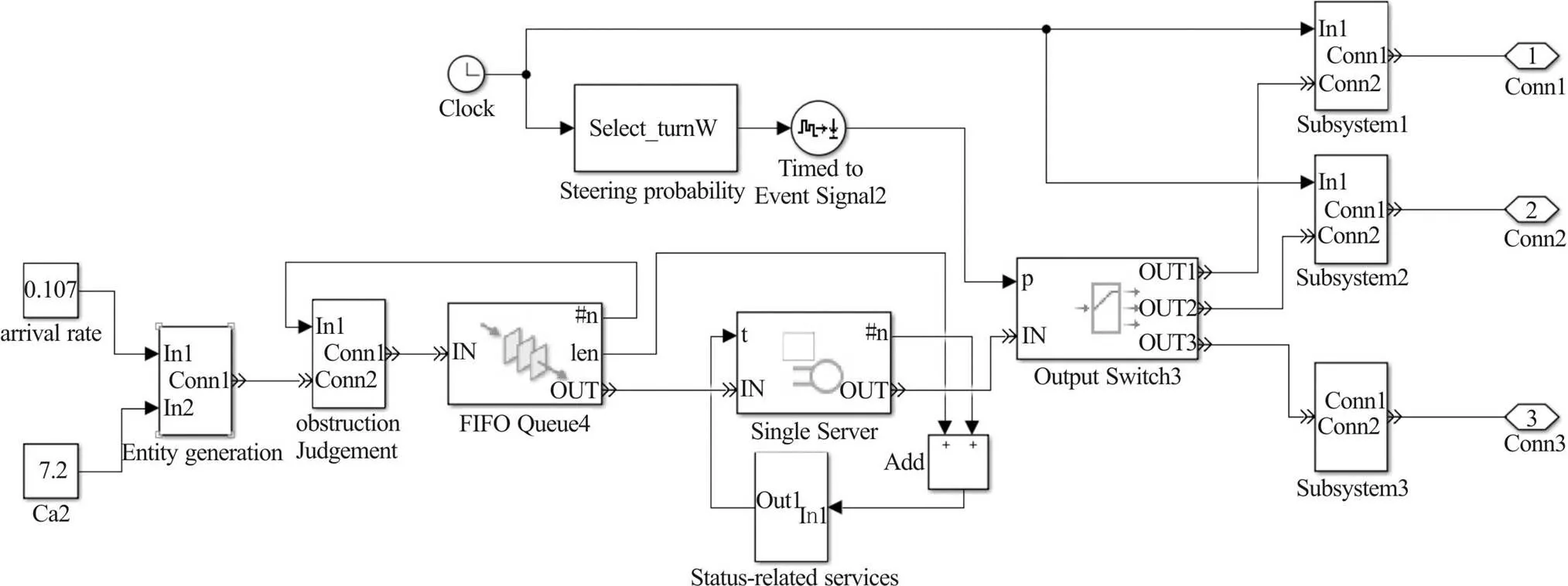
图4 交叉口进口道离散事件仿真模型

PH分布在S函数中实现，通过计算PH分布的两个输入参数，车辆的到达率和到达间隔的变异系数可得。

2.2.2 状态相关服务

根据以上分析可知，车辆在生成后，将在路段、进口道及出口道中运行，运行时间与路段、进口道、出口道处车辆数有关，即车辆在路段、进口道、出口道处接受服务时，服务时间均与当前系统状态相关。

车辆在路段处生成后，在判断车辆数量小于路段容量后，车辆会经路段前往进口道，再通过进口道进入出口道，最后离开交叉口。当车辆到达流通设施后，会形成队列等待服务，再经过服务离开此设施前往下一个设施。为实现这一过程，将借用Simulink中的Single_Server模块和FIFO_Queue模块，将生成的实体储存在FIFO_ Queue模块中，经FIFO_Queue前往Single_Server模块进行服务，在服务完毕后，实体将被送入其他设施中完成后续过程。在FIFO_Queue模块和Single_Server模块的作用下，流通设施的自由空间减少，其他实体通过设施的速度也被延迟。如果路段内的车辆数已经达到其容量，新生成的车辆不能进入路段的服务过程，为保证进入路段服务过程及进口道的车辆不会超过容量，利用Output_Switch模块为不能进入路段的车辆提供另一条路线。

状态相关的服务时间通过S函数得以实现。将FIFO_Queue模块与Single_Server模块中实体的数量作为输入量，通过流通设施车道数及车道长度计算容量，通过式（10）可得当前系统状态影响下的系统服务率，通过PH分布可得服务时间。借用S函数编程实现状态相关服务。

2.2.3 相位配时

由于交叉口处车辆的运行存在左转、右转、直行三个状态，且每个状态均受相位配时限制，借用S函数及Output_Switch模块及Enabled_ Gate模块实现相位配时及车辆左直右转。

3 实例分析

3.1 交叉口介绍

选取实例交叉口进行仿真分析，具体交叉口及相位配时方案如图5所示。

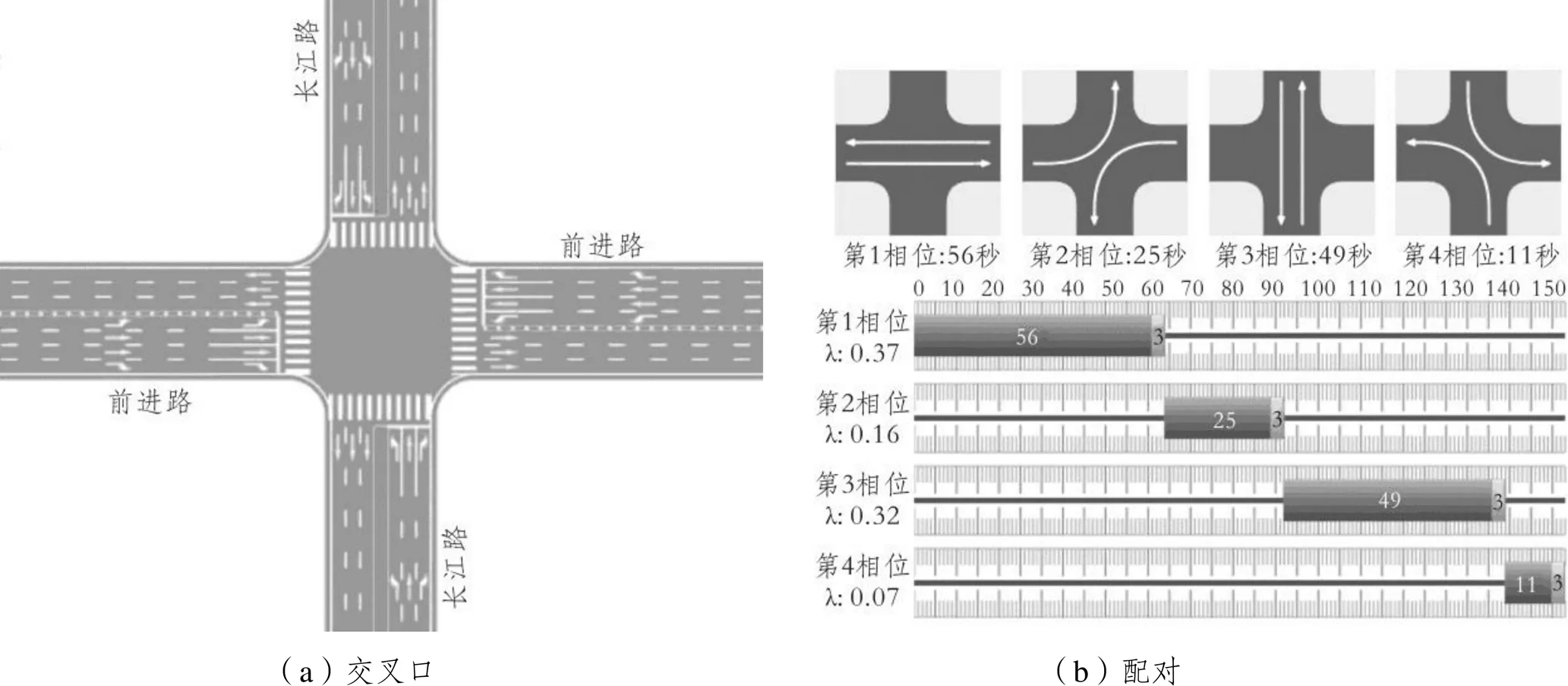
图5 实例交叉口及配时

3.2 参数计算

为合理拟合车辆到达，需计算交叉口车辆到达率、平方变异系数等相关参数。

各交叉口的进口道长度为规范确定，路段长度为实际测量。在GB50647—2011《城市道路交叉口规划规范》中有对不同等级道路相交时展宽段长度的规定，见表2。

根据公式（4），结合各路段长度，可计算路段及左转、直行、右转进口道和出口道的容量。

在仿真中，交叉口及路段相关参数如表3所示。

表2 不同等级道路相交时展宽段长度的规定

表3 仿真参数设置

Tab.3 Setting of simulation parameters

3.3 建模仿真

在已搭建仿真建模平台基础上，输入各项参数，可得实例交叉口仿真模型。

3.4 仿真分析

利用Simulink搭建仿真模型进行仿真，仿真时间设为1 h。对实例交叉口进行1 h仿真，统计系统内各进口道系统状态（车辆数），见图6。

根据上述实验结果，可得到以下几点结论：

（1）四个方向左转及直行进口道中系统状态均呈现周期性，这是由于直行及左转进口道内车辆运行受信号配时限制，一个周期内，直行或左转均只放行一次。

（2）交叉口东进口方向及西进口方向左转车辆数明显小于直行，这是由各方向车辆的到达率和转向比决定的，转向比例不同，则各方向系统状态不同。

（3）仿真结果中统计出的系统状态可以明显反映交叉口车辆的周期性变化和车辆转向比例的趋势。

当交叉口相关参数（路段容量、路段长度、车道数、信号配时）给定时，到达率不同，车道内的系统状态会存在区别。保证车辆到达时间间隔的平方变异系数和交叉口相关参数不变，改变车辆到达率，统计不同到达率下系统状态，如图7所示（以西进口道为例）。

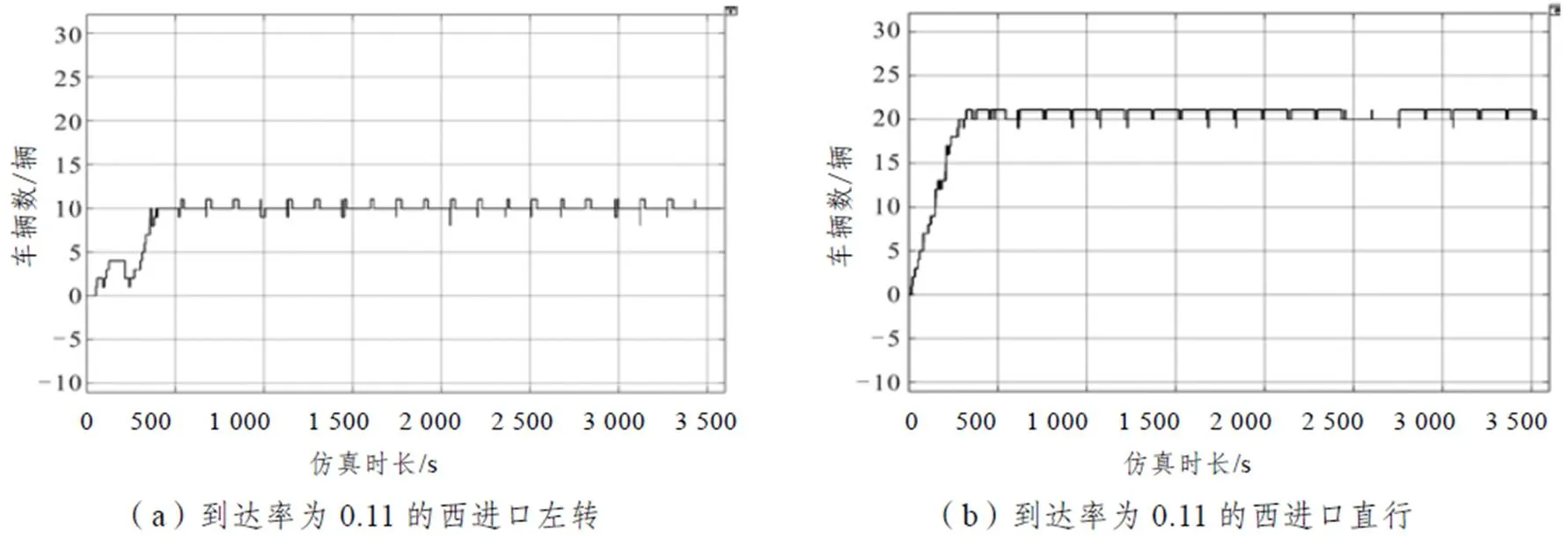
根据上述实验结果，可得到以下几点结论：

（1）系统内车辆到达率提高，系统到达稳定状态所需时间变短。

（2）因西进口道中，直行车辆所占比例最多，提高车辆到达率时，直行车辆达到系统容量所需时间最短。

（3）在到达率一定情况下，系统状态达到稳定后，存在周期性波动。因系统状态为排队阶段状态及服务阶段系统状态，服务率与系统状态直接相关，系统状态的变化会在一定程度上影响服务率，服务率反之影响系统状态，进而呈现系统状态的周期性波动。

4 结 论

准确模拟交叉口处车辆运行，对交叉口信号配时优化、交叉口设计等具有重要意义。本文将交叉口抽象为排队系统，考虑交叉口处容量有限，车辆到达率及交叉口服务率均服从PH分布，车辆通过交叉口时，通过时间具有状态相关性，建立PH/PH（）/1/2的排队系统。在排队模型的基础上，利用SimEvents搭建离散事件仿真模型，并进行交叉口离散事件仿真。仿真结果表明：（1）仿真模型可以较好地模拟车辆通过交叉口时由于受信号控制影响产生的周期性，反映不同方向车辆转向比趋势；（2）仿真模型可以模拟车辆到达周期性和各方向车辆转向比不同，与实际情况较为相近；（3）系统到达稳定状态的所需时间与车辆到达率存在关系，随着车辆到达率的增加，系统内达到稳定状态所需时间变短。

本文中，车辆到达交叉口时的到达率及变异为定值，但在实际中，车辆到达具有时变性，考虑到达率时变性的排队系统的建立及离散事件仿真模型的建立还有待后续进一步研究。

[1] TEKNOMO K. Application of microscopic pedestrian simulation model[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2006, 9 (1): 0-27.

[2] ILATI G, SHEIKHOLESLAMI A, HASSANNAYEBI E. A simulation-based optimization approach for integrated port resource allocation problem[J]. Promet-Traffic & Transportation, 2014, 26 (3): 243-255.

[3] CLIFFORD P. Passenger simulation modelling in station planning and design[J]. WIT Transactions on The Built Environment, 1996, 20: 229-237.

[4] HOOGENDOORN S, BOVY P H L. Simulation of pedestrian flows by optimal control and differential games[J]. Optimal Control Applications and Methods, 2003, 24 (3): 153-172.

[5] ZHU J, HU L, JIANG Y, et al. Circulation network design for urban rail transit station using a PH (n) /PH (n) /C/C queuing network model[J]. European Journal of Operational Research, 2017, 260 (3): 1043-1068.

[6] 张改. 考虑一般到达的信号交叉口自适应配时优化方法[D]. 成都: 西南交通大学, 2013.

[7] 李晓晨. 考虑动态客流的地铁车站售检票设施系统优化配置[D]. 成都: 西南交通大学, 2018.

[8] 胡路. 考虑稳定性的城市轨道交通车站交通服务设施系统优化配置理论与方法[D]. 成都: 西南交通大学, 2014.

[9] SMITH J M G. State-dependent queueing models in emergency evacuation networks[J]. Transportation Research Part B: Methodological, 1991, 25 (6): 373-389.

[10] OSORIO C, YAMANI J. Analytical and scalable analysis of transient tandem Markovian finite capacity queueing networks[J]. Transportation Science, 2017, 51 (3): 823-840.

[11] YUHASKI S J, SMITH J M G. Modeling circulation systems in buildings using state dependent queueing models[J]. Queueing Systems, 1989, 4 (4): 319-338.

[12] CHEAH J Y, SMITH J M G. Generalized M/G/C/C state dependent queueing models and pedestrian traffic flows[J]. Queueing Systems Theory and Applications, 1994, 15(1-4): 365-386.

[13] JAIN R, SMITH J M G. Modeling vehicular traffic flow using M/G/C/C state dependent queueing models[J]. Transportation Science, 1997, 31 (4): 324-336.

[14] SMITH J M G, CRUZ F R B. M/G/c/c state dependent travel time models and properties[J]. Physica A: Statistical Mechanics and its Applications, 2014, 395: 560-579.

[15] 孙晓峰, 王中杰. 基于MATLAB/SimEvents的网络仿真研究[J]. 电脑知识与技术 (学术交流), 2007 (23): 1254-1257, 1269.

Discrete Event Simulation Modeling of Urban Intersection Considering State-dependent Services

QI Xin1，HU Lu2, 3，ZHAO Bin2, 3，TANG Xiao-pei2, 3

（1. Tianjin Municipal Engineering Design & Research Institute, Tianjin 300051, China; 2. School of Transportation and Logistics Southwest Jiaotong University, Chengdu 611756, China; 3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China）

Accurate simulation of vehicle operation at intersections is of great significance in signal-timing optimization and intersection design. The queuing model of an intersection can accurately simulate the arrival of vehicles and the services of the intersection. First, Phase-Type（PH） queuing model can proximally access arbitrary reaching laws and service laws. Second, when vehicles arrive at an intersection, the capacity of the intersection is limited. Third, when a vehicle passes through an intersection, the passing time is state-dependent. Considering these three points, a queuing model of PH/PH（）/1/2is established. The intersection is translated into DES（Discrete-Event Simulation）models, in which the arrival and service processes of the vehicles are based on the PH random variations. The proposed DES model fully considers the state-dependence of lane service. Simulink is used to build the simulation model, and finally, the DES model of an intersection considering state-related services is established. The results show that the proposed model can accurately represent the periodicity of vehicles passing through an intersection and objectively reflect the vehicular traffic situation.

traffic engineering; discrete-event simulation; queuing system; urban intersection; Phase-Type distribution

U491.51

A

10.3969/j.issn.1672-4747.2020.01.018

1672-4747（2020）01-0133-13

2019-01-15

成都市科技项目（2017-RK00-00362-ZF）；西南交通大学研究生学术素养提升计划（科创竞赛培育）专题项目（2019KCJS46）

齐心（1993—），女，河南濮阳人，硕士，助理工程师，研究方向为交通工程，E-mail：2016200893@my.swjtu.edu.cn

齐心，胡路，赵斌，等. 考虑状态相关服务的城市交叉口离散事件仿真建模[J]. 交通运输工程与信息学报，2020，18（1）：133-145.

（责任编辑：李愈）