基于多线耦合的城市轨道交通时刻表仿真评估

晏浩哲，马 驷

基于多线耦合的城市轨道交通时刻表仿真评估

晏浩哲1,2，马 驷1

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 四川省交通运输发展战略和规划科学研究院，成都 610031；）

时刻表的设置对于城市轨道交通系统的运营有着重要影响, 为了使城市轨道交通系统的时刻表制定更加灵活可控, 提出一种基于Anylogic仿真的多线耦合状态下时刻表协调评估的新方法。通过Anylogic软件将线路间隔与首趟列车到达时刻作为变量建立多线耦合的网络仿真模型, 并以成都地铁网络为实例结合现行时刻表建立不同备选方案, 利用熵权法与加权平均法结合的评价模型对不同方案站台区域密度与平均候车时间两项指标进行对比评价, 最终得出较优时刻表, 并分析其特点得出线路间隔与首趟列车到达时刻间的协调优化关系。

城市轨道交通网络；Anylogic仿真；时刻表协调评估优化；网络运输组织优化

0 引 言

随着城市轨道交通系统的不断发展，我国城市轨道交通系统运营逐渐由单线步入网络化模式，城市轨道交通系统多线耦合一般指不同线路在换乘站交织所逐步形成的网络化状态。在网络化背景下乘客换乘行为越发复杂，传统单线运输组织模式很难满足网络条件下的客流需求，而列车时刻表作为组织列车运行的基础，其协调与否将直接影响整个网络的运营效果。

目前国内关于时刻表协调优化评估的研究大多通过建立静态数学模型的方法求解，存在着一定的缺陷，主要的研究思路为通过建立整数规划模型对网络中单个换乘站时刻表进行评估优化[1-7]。而国外相关研究起步早，随着相关理论的完善，研究重点逐渐向节能[8]、智能数据采集[9]、系统仿真[10]等方面发展。既有研究在评估优化过程中对客流的随机变化、轨道交通的网络效应、数据的动态输出等因素都未能充分考虑，在规模和方法上都是可以改进的。

因此，考虑到目前研究的局限性，本文选择Anylogic软件仿真的方法基于多线耦合状态对时刻表协调评估进行研究，选择工作日早高峰（8:00~8:30）的数据建立城市轨道交通网络模型，将列车间隔与首趟列车到达时刻综合考虑，设置不同的备选方案并输出站台密度、换乘等待时间指标，采用熵权法与加权平均法结合的评估模型对不同方案进行分析并得出时刻表协调的内在关系。

1 时刻表协调评估模型

时刻表协调评估模型的构建主要分为时刻表协调指标选取、指标权重确定、综合评价方法的确定三步。

1.1 协调指标选取

已有研究中时刻表协调指标包括客流密度、候车时间、设施设备利用率等[11-16]，但最终各个指标都需要从乘客的角度来反映车站服务水平。结合运营实际与既有研究，本文选择站台区域密度与平均换乘时间两项时刻表协调指标。

站台区域密度能直接反映站台拥挤程度，作为乘客候车的集中区域，其密度过大会直接影响车站的客运组织，同时会造成严重的安全隐患。乘客候车时间既可以从乘客体验的角度反映车站的服务水平，也可以从网络的角度反映时刻表的协调性。由于本文所选协调时段为工作日早高峰，在高峰期间车站客流压力大，首要任务是完成乘客的集散，因此以站台区域密度为主要指标进行评估，在保证站台区域密度较小时尽量控制平均候车时间最短。本文选用时刻表协调指标如表1所示。

表1 时刻表协调指标

Tab.1 Index of schedule coordination

1.2 指标权重确定

由于本文所涉及的仿真指标数量较少，采用客观权重法有较高的精确度，本文选择含义明确且接受度较高的熵权法确定评价指标权重。熵权法主要操作步骤可归纳为：

（1）数据标准化处理

（2）指标信息熵计算

其中，P表示归一化后各方案值所占比例：

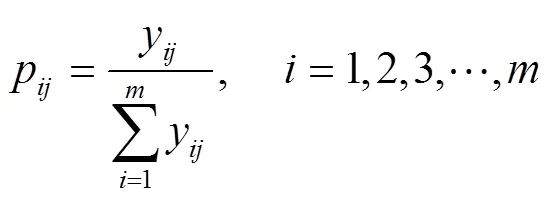
（3）指标权重计算

熵权法确定指标权重的计算公式如下：

1.3 综合评价方法确定

对每个方案计算综合评价值后，按照从大到小进行排序，大小排列的顺序即为不同方案的推荐程度。

2 网络仿真建模

网络仿真模型需要同时兼顾行人行为与列车行为，Anylogic作为多方法建模软件，其内嵌的社会力模型能较好地满足网络仿真的需求。仿真建模主要包括车站环境建模、行人行为建模、多线耦合建模和数据输出建模四个部分。

2.1 车站环境建模

首先，需要通过车站布置CAD图确定面向乘客的车站服务区域；接下来，利用Anylogic行人库中空间标记模块来描绘车站环境。不同模块对应的功能见表2。

表2 车站建模相关模块

Tab.2 Station modeling related modules

在软件中完成车站环境描绘后还需要对模块属性进行设置，在属性中可以对线服务数、队列数、队列类型、服务类型、排队策略进行设定。

2.2 行人行为建模

行人行为建模的主要目的即以车站环境建模为基础，建立行人在车站的逻辑行为。将行人行为分为进站行人行为、出站行人行为、换乘站的换乘行人行为，三种不同类型的行人行为流程如图1所示。

图1 行人流程图

建立行人逻辑行为主要通过行人库的模块功能实现，不同模块主要功能如表3所示。

表3 行人建模相关模块

Tab.3 Pedestrian modeling related modules

根据行人在站的不同行为，构建基本的行人逻辑建模，如图2所示。

图2 基本行人逻辑

完成行人逻辑建模后首先需要将其与已建立好的车站环境建立对应关系，一般做法是在模块的属性设置中通过图形化定义实现。此外在属性界面中还需要设置行人到达速率、到达方式、行人速度、行人延迟方式、行人服务类型等。在行人建模的过程中需要注意既有模块中并没有考虑列车容量限制带来的乘客滞留现象，需要通过“Ped Wait”与“Delay”模块的组合来实现，如图3所示。

“Delay”模块的最大容量代表了当前候车区域可进入列车的人数，主要由列车容量限制与列车已有人数共同影响。具体实施方法是在每一站记录进入列车的人数并计算列车已有乘客数量从而设置后站“Delay”模块的最大容量。举例来讲，例如存在A、B两站，A往B为下行方向，下行方向B站站台可进入列车的人数由列车在A站已有乘客数与A站上下车人数共同决定。

行人建模过程中使用的相关参数如表4所示。其中uniform表示正态分布，normal表示均匀分布。

表4 仿真相关参数

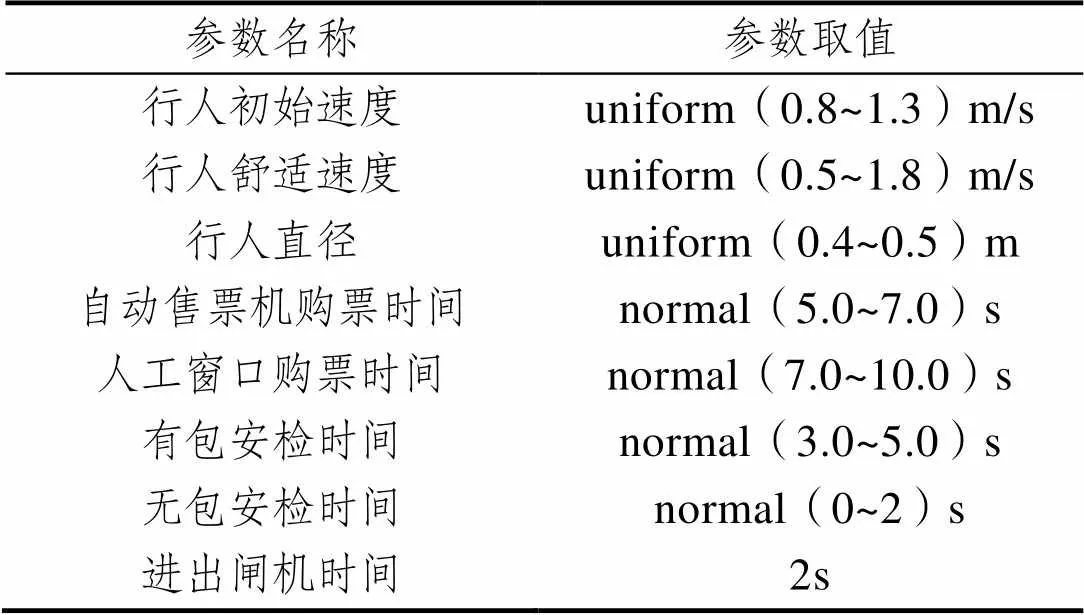
Tab.4 Related simulation parameters

2.3 多线耦合建模

多线耦合建模主要实现将各个独立车站协同一体的功能，仿真模型中主要通过时刻表将不同车站联系起来并对列车与行人行为进行控制。为了使仿真模型可以在任意时段存在通用性，首先设置网络初始状态，主要包括当前网络已有的区间客流与候车人数限制。在列车到达的时刻通过inject函数实现乘客到达车站，同时使用stopDelayForAll结束当前乘客的候车行为，对应的行人逻辑中也需要将“Ped Source”的到达根据设置为inject（）函数调用，“Delay”模块中的类型设置为直至调用stopDelay（）。在列车到达事件中，线路间隔与首趟列车到达时刻为变量，建模过程中主要用到的函数如表5所示。

表5 建模主要函数

Tab.5 Main modeling functions

针对上节中的例子结合容量限制功能对A站下行方向列车到达事件进行设置，如图4所示。

图4 列车到达事件设置

2.4 数据输出建模

Anylogic软件提供了丰富的数据输出手段，包括了图形化的数据输出。结合本文相关内容，主要输出的数据为站台区域密度、乘客平均候车时间。数据输出过程中主要用到的模块如表6所示。

表6 数据输出相关模块

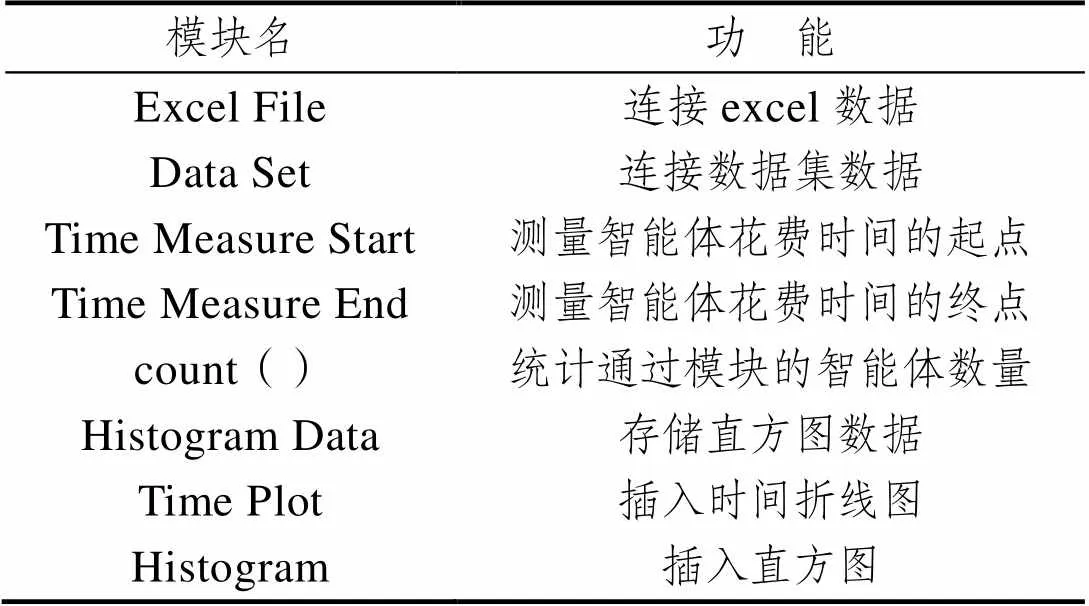
Tab.6 Data output related modules

站台区域密度，首先利用环境建模中的矩形区域与多边形区域描绘出各站站台范围，之后使用行人库中的“Ped Area Descriptor”选择相应区域，从统计功能中添加“数据”模块存放密度数据，其值为对应的“Ped Area Descriptor”的density（）属性。

乘客平均候车时间，在需要测量时间的流程两端分别添加流程库中的“Time Measure Start”和“Time Measure End”模块，模型运行后时间数据将会以数据集的形式存放在“Time Measure End”模块中。

统计两类数据后利用“Excel File”模块通过writeDataSet（）函数将数据输入到excel表格中。

3 实例分析

3.1 仿真模型建立

本文选择成都地铁网络中天府广场、中医大省医院、骡马市三个换乘站之间形成的多线耦合城市轨道交通网络建模。其中一号线上行方向为天府广场到骡马市，二号线上行方向为中医大省医院到天府广场，四号线上行方向为中医大省医院到骡马市。由于高峰时段客流压力大，时刻表设置不同所造成的影响也最大，因此固定仿真时段为工作日早高峰（8:00~8:30），采取AW2定员载客数1 468人作为列车容量限制。固定网络区间运行时分不变，如图5所示。

图5 网络仿真示意图

表7 时刻表协调备选方案（单位：s）

Tab.7 Schedule coordination options（unit：s）

3.2 结果分析

采用上文提出的熵权法与加权平均法结合的评价模型对不同方案进行分析，输出不同方案评分的综合评价值如图6所示。

在18种时刻表中，最优时刻表为方案2，成都地铁现行方案1评分略低于方案2，不同方案评分基本可分为60~70、70~80、80以上三个等级。接下来输出站台最大密度数据，由于非换乘站并不是协调评估的主要控制点，因此仅输出换乘站相关数据，如图7所示。

图6 不同方案综合评价值对比

图7 站台最大密度（单位：人/m2）

结合综合评价结果分析相关数据可以发现方案2将一号线站台客流密度维持在较低范围，同时一定程度牺牲了四号线站台客流密度。而评分较低的方案16正好与方案2相反，即首先保证了四号线站台密度。因此可以发现一号线站台密度是高峰时段的重要控制指标，接下来输出平均候车时间数据。

就平均候车时间而言（如图8），时刻表1、2、3、4、5、6、13、14、15候车时间都是相对较低的。但结合综合评价结果与站台密度指标可以发现在高峰时段站台密度指标优先于平均候车时间，在满足站台密度指标的前提下进行平均候车时间的调整是相对科学的。将最优时刻表方案2与现行时刻表对比分析，四号线列车到达时刻早于一、二号线，且一、二号线列车到达时刻相对接近。

图8 平均候车时间对比（单位：s）

结合仿真结果可得出在协调过程中，应该首先满足天府广场与骡马市换乘到一号线的换乘协调，一号线间隔为重点协调对象，并且只要保证一号线间隔是三者中最小值时即可有较优效果，而二号线与四号线间隔整体影响差异不大。此外应使一号线列车到达时刻早于二号线列车到达时刻且上下行方向到达时刻相对接近。

4 结束语

本文利用Anylogic软件建立基于多线耦合的成都地铁网络的轨道交通网络仿真模型，通过输出站台密度与平均候车时间数据对备选方案进行对比分析，结果表明一号线间隔取最小且列车到达时刻最早，同时上下行到达时间相对接近是较优的协调方向。基于网络的时刻表协调是一个十分复杂的过程，而本文仅以6座车站为对象进行研究，并且对于列车停站时间也进行了相应简化。如何将客流分配的不确定因素考虑进仿真模型中是进一步研究需要思考的问题。

[1] 蔡涵哲. 网络化条件下城市轨道交通行车组织优化问题研究[D]. 北京: 北京交通大学, 2012.

[2] 张迅. 基于换乘协调的城市轨道交通换乘站列车衔接优化研究[D]. 北京: 北京交通大学, 2014.

[3] 马超云. 城市轨道交通换乘站列车时刻表的协调和优化[D]. 北京: 北京交通大学, 2010.

[4] 张铭, 徐瑞华. 轨道交通网络列车衔接组织的递阶协调优化[J]. 系统工程, 2007, 25(9): 33-37.

[5] 周艳芳, 周磊山, 乐逸祥. 城市轨道网络换乘站列车衔接同步协调优化研究[J]. 铁道学报, 2011, 33(3): 9-16.

[6] 卞兆洋. 城市轨道交通网络化运营组织协调优化[D]. 成都: 西南交通大学, 2015.

[7] 李玉芳, 高越. 轨道交通网络化列车首末班车衔接协

[8] 调方案研究[J]. 城市建设, 2011(1): 277-277.

[8] ERFAN H, ARMAN S, SOHEIL M, et al. An integrated. Simulation model and evolutionary algorithm for train timetabling problem with considering train stops for praying[C]// Simulation Conference (WSC). Berlin: IEEE, 2012.

[9] WEI Z, HAO H, HUANG Z. Calibrating rail transit assignment models with genetic algorithm and automated fare collection data[J]. Computer-Aided Civil and Infrastructure Engineering, 2014, 29(7): 518–530.

[10] YANG X, LI X, GAO Z Y, et al. A cooperative scheduling model for timetable optimization in subway systems[J]. IEEE Transctions on Intelligent Transportation systems, 2013, 14（1）:438-447.

[11] 马语佳, 马驷, 谢冰如. 大型高速铁路客运站客运设施配置仿真优化[J]. 铁路计算机应用, 2016, 25(3): 12-16.

[12] 李洪旭, 李海鹰, 樊校, 等. 基于Anylogic的地铁车站集散能力仿真分析评估[J]. 铁路计算机应用, 2012, 21(8): 48-50.

[13] 陈立扬, 宋瑞, 李志杰, 等. 基于Anylogic的地铁站站厅层设施布置仿真研究[J]. 交通信息与安全, 2013(5): 25-30.

[14] 苏星燕. 城市轨道交通换乘站运营协调效率的评价研究[D]. 长沙: 中南大学, 2010.

[15] 张铭, 吴彦颖. 城市轨道交通换乘枢纽运营协调效率评价[J]. 都市快轨交通, 2009, 22(5): 24-27.

[16] 彭沙沙, 吴小萍, 梅盛. 基于GIS的城市轨道交通与土地利用协调研究[J]. 铁道工程学报, 2011, 28(1): 76-79.

Simulation and Evaluation of An Urban Rail Transit Timetable Based on Multi-line Coupling

YAN Hao-zhe1, 2，MA Si1

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. Institute of Transportation Development Strategy & Planning of Sichuan Province, Chengdu 610031, China)

Timetable scheduling has an important effect on the operation of urban rail transit systems. Based on anylogic simulation, this study proposed a new method for optimizing flexibility and control in solving the problem of timetable coordination and evaluation. First, we established a multi-line coupling network simulation model using train intervals and first train arrival times as the variables. Then, taking the Chengdu metro network as an example for building a network model, we designed different schedules based on the current timetable. We used the evaluation model combined with weighted entropy and weighted average to compare and evaluate the density and average waiting time of different platforms, finally, we attained a better timetable. Further, by analyzing its characteristics, we obtained the coordination optimization relationship among the variables.

urban rail transit network; Anylogic simulation; timetable evaluation and optimization; optimization of network transportation organization

U293.1

A

10.3969/j.issn.1672-4747.2020.01.015

1672-4747（2020）01-0111-09

2019-01-18

成都轨道交通5号线一、二期工程客流预测（05CBHT-FW-2019-002）

晏浩哲（1994—），男，四川成都人，硕士，研究方向为运输组织优化，E-mail：120526259@qq.com

晏浩哲，马驷. 基于多线耦合的城市轨道交通时刻表仿真评估[J]. 交通运输工程与信息学报，2020，18（1）：111-119.

（责任编辑：李愈）