城市轨道交通运营设备安全风险评价

高 鹏，唐 昭，杨坤洪，程学庆,2，管邦宁

城市轨道交通运营设备安全风险评价

高 鹏1，唐 昭1，杨坤洪1，程学庆1,2，管邦宁3

（1. 西南交通大学，交通运输与物流学院，成都 611756;2. 深圳市坪山区交通轨道管理中心，深圳 518118;3. 南京邮电大学，计算机学院，南京 210023）

城市轨道交通作为城市经济发展的重要载体, 其运营设备的可靠运转是城市轨道交通运行安全的有效保证。本文以某市轨道交通体系中的供电设备为研究对象, 采用最小二乘法、熵值法分别对运营设备指标进行主、客观赋值, 并结合博弈论思想进行综合指标权值计算, 最终通过梯形模糊数理论对供电设备进行风险评估。评估结果表明, 设备老化、故障是轨道交通安全事故的主要诱因, 为了保证该城市的轨道交通运营安全, 需要加大、加紧对该城市轨道交通运营设备的状态跟踪与监控。

城市轨道交通; 运营设备; 最小二乘法; 熵值法; 博弈论; 梯度模糊数

0 引 言

随着城市轨道交通网络不断完善，城市轨道交通运营服务也有了质的飞跃。城市轨道交通设施主要建设在大中型城市的中心地带及周围地区，车站分布的日益密集、客流量的与日俱增以及线路间耦合度的逐渐增强，均导致我国轨道交通正面临着严峻的安全挑战。轨道交通运营安全是轨道交通系统管理中的关键环节，据不完全统计，除了一些突发事故外，城市轨道交通运营设备是导致安全事故发生的主要原因，运营设备的安全状态直接影响着轨道交通运营安全[1]。因此，应对城市轨道交通运营设备的检修与监察严格把关，实时监控。

根据国务院办公厅2018年下发的《关于进一步加强城市轨道交通规划建设管理的意见》文件要求，结合当前轨道交通面临诸多潜在风险的现状，采取有效的安全风险评价方法，预先分析可能引发危害的设备因素至关重要。代宝乾、汪彤等[2]运用不同尺度对轨道交通事故做了准确的划分，利用风险理论建立评估模型对地铁的危险性进行了量化研究。张辉等[3]运用结合层次分析法与模糊综合评估方法，综合各方面因素对上海轨道交通工程风险进行了评估研究。潘科等[4]等利用多级可拓评价方法分析了影响地铁安全的危害因素，并查找出影响地铁运行的安全隐患，定性分析了影响地铁运行安全的薄弱环节。聂菁等[5]依据风险评估矩阵构建了风险评估模型，然后运用模糊综合评价法对福州轨道1号线整个动态施工方面进行风险评价。应国柱等[6]通过修正的模糊层次分析法确定指标的权值，并利用二级非线性模糊综合评价模型对合肥地铁1号线工程进行风险评价。

目前，相关安全研究大部分都只采用了主观研究或客观研究，这种单一的方法并不能全面准确地进行安全评价，而且不能有效地反映安全性能。本文通过融合最小二乘法和熵值法，使指标赋权达到主、客观的统一，进而使评价更可靠，建立梯形模糊数风险评估模型，能够权威有效地进行指标评价，研究结果能够反映实际存在的问题。

1 运营设备影响因素

在城市轨道交通系统中，运营设备种类繁多，数量庞大。运营基础设备分为固定设备（车站、线路、信号设备）和移动设备（机车、车辆、通信设备）；运营安全技术设备分为安全监控和安全监测设备；其他还有自然灾害预报及防治设备、事故救援设备等[7]。

由于时间和环境的影响，运营设备会出现精度降低、性能下降的问题，这些将直接影响轨道交通系统的正常运转。根据对近年来国内外轨道交通运营事故事件的分析，设备风险影响因素如图1所示[8]。

图1 设备运营影响因素

2 运行风险评估模型

在运行风险评估的指标系统中，通过评估分析各类因素对运营设备运行安全的影响程度进行指标划分[9]。本文综合考虑了主观赋权法、客观赋权法的优缺点，结合两种赋权方法并通过组合赋权法确定指标的权值。

2.1 主观权值

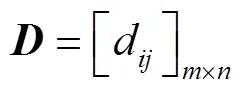
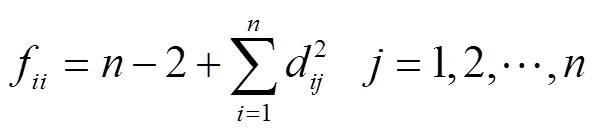
模型求解得：

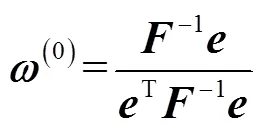
2.2 客观权值

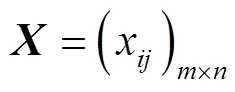
计算综合指标前，需要对各项指标进行标准化处理，即指标归一化，将指标的绝对值转化为相对值，其中正向指标和负向指标标准化处理方法如下所示[11]：

（1）正向指标公式为：

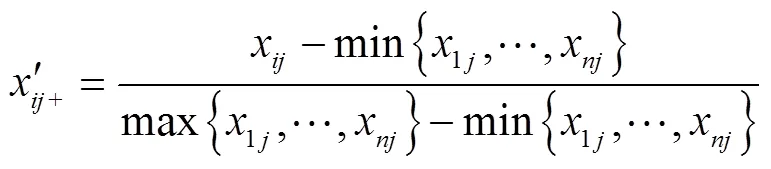
（2）负向指标公式为：

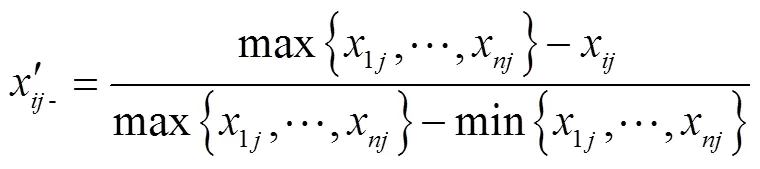
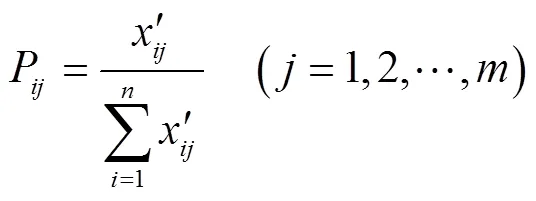
2.3 组合权值

对运营设备指标进行组合赋权可以综合主、客观赋权的优缺点，其中博弈集结模型方法可以规避决策者的个人意向，并利用客观数据对决策的贡献度进行综合评价。组合权值的基本思想是在不同方法中寻找最小化组合权值与各个权值之间的偏差，最终达成一致或妥协，即偏差之和最小[12]。计算组合权值步骤为：

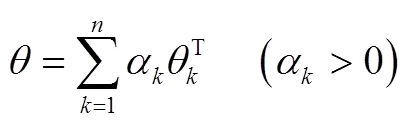
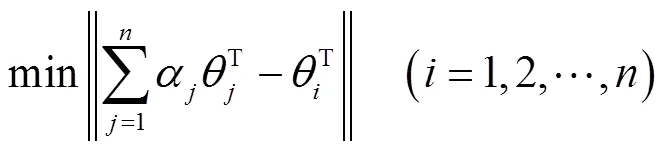
对应线性方程组为：

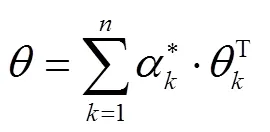
2.4 梯形模糊数风险评估模型

采用梯度模糊数风险评估模型对设备指标进行评价，利用梯形模糊数的评估理论与方法能够科学有效地进行指标分析，其计算步骤如下表示：

（1）设定模糊语言等级以及对应的模糊语言评判和规范化梯形模糊数；

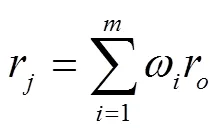
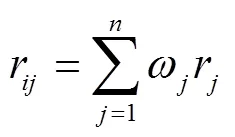
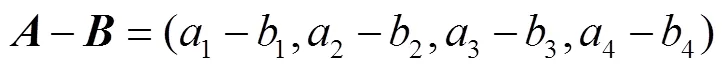
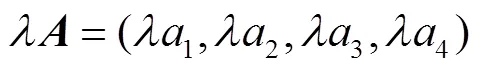
按照梯度模糊数运算法则（20~23），计算相应模糊语言等级距离，选取最小值作为评估结果。

3 运营设备风险评估

3.1 评估指标体系构建

城市轨道交通运营设备运营风险评估指标体系应在科学性、全面性、主导性、操作性及可比性原则的指导下，严格遵循评估指标体系的歩骤流程，建立综合安全性水平结构体系。由于运营设备数据有限，根据2017年度某运营单位设备事故统计（其中供电设备作为运营设备中最容易发生事故的一环），本文选取供电设备作为研究对象。以供电系统为例将风险评估指标体系划分为三个层次：目标层、一级指标层、二级指标层进行了分析，从中筛选出4个一级指标以及13个二级指标，其中一级指标是按照供电设备在整个供电系统中的重要程度选取，能够有效反映整个供电系统。供电设备安全风险评估指标体系见表1所示[13-15]：

表1 供电设备安全风险评估指标体系

Tab.1 Power supply equipment safety risk assessment index system

3.2 指标体系权值求解

（1）指标体系的主观权值

利用重要性标度方法进行比较，构造子集层比较矩阵，如表2所示。

Tab.2 Matrix importance scale method

计算二级指标对应的主观权值见表3所示：

由主观权值表可以看出，通信信号设备水平中，联锁系统权值占比较大；站台门设备水平中，电气类故障和其他故障权值占比较大；FAS/BAS系统水平中，FAS系统故障权值占比较大；而水电专业设备水平中，低压配电类故障占比较大。

表3 评价指标子集A的主观权值

Tab.3 The subjective weight index of evaluation indicator subset A

（2）指标体系的客观权值

对运营公司2015—2017年轨道交通供电设备事故发生案例进行统计，见表4所示。

表4 供电设备近3年故障次数

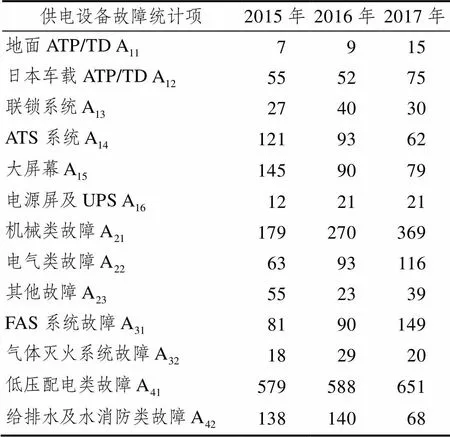
Tab.4 The number of power supply equipment failures in the past 3 years

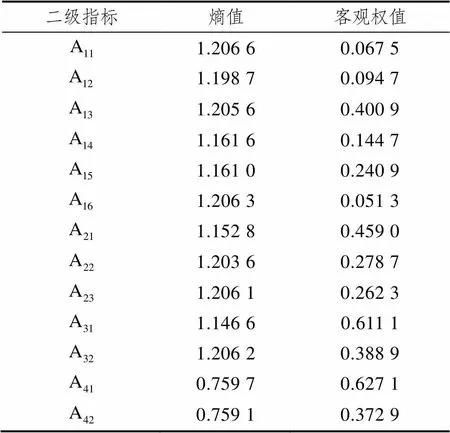
对供电设备指标数进行计算，得到各项指标的客观熵权见表5所示。

表5 评价指标子集A的客观权值

Tab.5 The objective weight index of evaluation indicator subset A

客观比较分析2015—2017年供电设备故障指标权重，由客观权值表可以看出，二级指标之间的客观权值相差不大，权值占比比较均衡。通信信号设备水平中，ATS系统以及大屏幕权值占比相对较低；FAS/BAS系统水平中，FAS系统故障权值占比相对较低。

（3）指标体系的组合权值

基于最小二乘法和熵值法算出的主观权值和客观权值，然后按照式（15）权向量集化模型改写成：

求得改进后最优解为：

对系统设备指标体系中子集层进行计算，得到各项指标的组合权值，见表6所示。

由组合权值表可以看出，基于主、客观权值两种方法的差异性，对权值进行组合赋权优化后得到的组合权值更加科学、合理。组合权值既协调了主、客观权值两者的差异，又很好地反映主观意愿和客观事实。二级指标中联锁系统、FAS系统故障、低压配电类故障权值占比较大。

表6 评价指标子集A的组合权值

Tab.6 The combined weight index of evaluation indicator subset A

3.3 运营设备安全风险等级评估

本文选取七个级别语言评估标度来进行规范化梯度模糊数计算，其转化关系见表7所示。

表7 梯形模糊数转化关系表

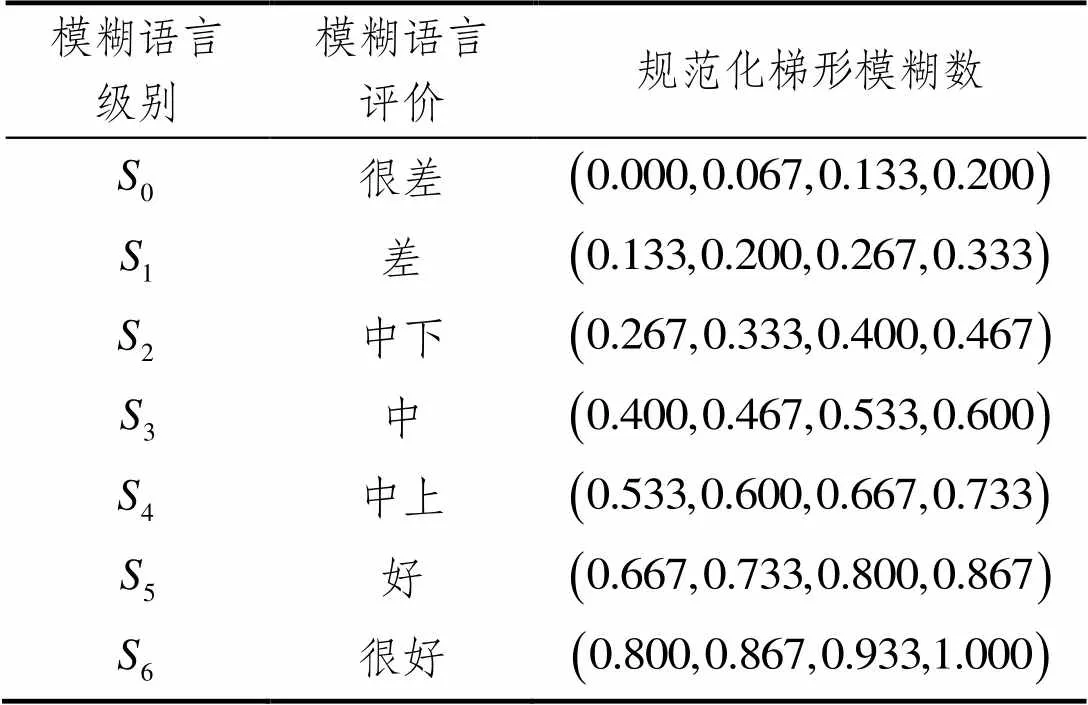
Tab.7 Trapezoidal fuzzy number conversion relationship table

表8 糊数指标的模糊语言评价集

Tab.8 Fuzzy language evaluation set

运用组合权值计算每项设备指标的综合评估梯形模糊数：

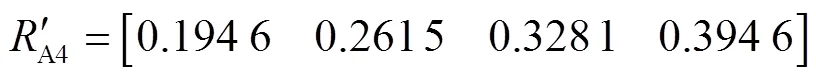
按照最近隶属度原则，计算规范化梯度模糊数的最短距离，结果如表9所示。

表9 评估结果与规范梯形模糊数的最短距离

Tab.9 The shortest distance and evaluation result of the standard trapezoidal fuzzy number

4 结 论

基于梯形模糊数理论风险评估模型，本文对某城市运营单位运营设备中的供电设备进行安全风险评价。评价结果显示四项一级指标规范化梯度模糊数的最短距离分别为：0.028 9、0.054 3、0.056 1和0.107 4，均处于中等风险水平，其中水电专业设备安全指标存在较为严重的风险。相比较近三年水电专业设备中，低压配电类平均故障频数达到606次、给排水及水消防类故障频数达到116次，这两项供电设备故障率占比较高，评价结果能够准确反映实际故障数。因此从供电设备可以反映出必须从技术设备上做好风险预防、风险监测、风险控制和应急处置等全链条工作，只有这样才能有效提升轨道交通安全保障水平。本文由于可用数据较少并且没有将环境人为等因素考虑进来，后续研究可以从大数据综合分析“人-机-环”三者因素，按照因素影响等级对城市轨道交通进行安全风险评价。

[1] 肖雪梅. 城市轨道交通网络化运营风险与安全评估——基于拓扑的方法[D]. 北京: 北京交通大学, 2014.

[2] 代宝乾, 汪彤, 秦跃平, 等. 基于事故理论的城市轨道交通风险评价模型研究[J]. 中国安全科学学报, 2007, 17(10): 156-159.

[3] 张辉, 李文勇, 倪志芳. 上海轨道交通12号线工程施工风险评估与管控措施研究[J]. 城市轨道交通研究, 2010, 13(11): 46-51.

[4] 潘科, 王洪德, 石剑云. 多级可拓评价方法在地铁运营安全评价中的应用[J]. 铁道学报, 2011, 33(5): 14-19.

[5] 聂菁, 苏会卫, 张念. 基于AHP的轨道交通施工风险模糊综合评价方法——以福州轨道交通1号线为例[J]. 自然灾害学报, 2014, 23(5): 246-252.

[6] 应国柱, 汪鹏程, 朱大勇, 等. 基于模糊综合评价模型的地铁施工风险评估[J]. 地下空间与工程学报, 2016, 12(2): 539-545.

[7] 任星辰. 城市轨道交通运营设备设施安全评价体系研究[D]. 北京: 北京交通大学, 2012

[8] 杨红梅. 城市轨道交通运行风险评估[D]. 重庆: 重庆大学, 2015.

[9] 黄雅坤. 城市轨道交通路网运营安全评价方法研究[D]. 北京: 北京交通大学, 2014.

[10] 韩信, 冷雪. 基于层次分析法和熵权法的高校奖学金评定——以四川文理学院为例[J]. 科技和产业, 2012, 12(11): 90-93.

[11] 李美娟, 陈国宏, 陈衍泰. 综合评价中指标标准化方法研究[J]. 中国管理科学, 2004, 12(z1): 45-48.

[12] 路遥, 徐林荣, 陈舒阳. 基于博弈论组合赋权的泥石流危险度评价[J]. 灾害学, 2014, 29(1).

[13] 刘强. 基于模糊理论的嘉阳小火车运营安全风险评价研究[D]. 成都: 西南交通大学, 2016.

[14] DONG S K, DONG H B, WAN C Y. Development and evaluation of a computer-aided system for analyzing human error in railway operations[J]. Reliability Engineering & System Safety, 2010, 95(2): 87-98.

[15] LI L, ZHANG H, WANG X, et al. Urban transit coordination using an artificial transportation system[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(2): 374-383.

Safety Risk Assessment of Urban Rail Transit Operation Equipment

GAO Peng1，TANG Zhao1，YANG Kun-hong1，CHENG Xue-qing1, 2，GUAN Bang-ning3

（1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China;2. Shenzhen Pingshan District Traffic Track Management Center, Shenzhen 518118, China;3. School of Computer Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, China）

Urban rail transit is an important conductor of urban economic development. Reliable performance of its operating equipment is an effective guarantee for the safety of urban rail transit operations. In this paper, the power supply equipment of a city’s rail transit system is scrutinized through research. The least square method and entropy method are used to perform the subjective and objective assignment of the operational equipment indicators, and are combined with game theory to calculate the comprehensive index weights. Further, the trapezoidal fuzzy number theory is incorporated to conduct a risk assessment of power supply equipment. The evaluation results show that equipment aging and failure are the main causes of rail transit safety accidents. In order to ensure the safety of rail transit operations in the city, it is necessary to increase and enhance the status tracking and monitoring of the urban rail transit operation equipment.

urban rail transit; operating equipment; least square method; entropy method; game theory; trapezoidal fuzzy number theory

U121

A

10.3969/j.issn.1672-4747.2020.01.012

1672-4747（2020）01-0091-08

2019-04-07

区域轨道交通协同运输与服务系统——区域轨道交通安全综合保障关键技术及装备（VP99QT1136Y18002）

高鹏（1993—），西南交通大学硕士研究生，研究方向：智能交通。E-mail：705405190@qq.com

高鹏，唐昭，杨坤洪，等. 城市轨道交通运营设备安全风险评价[J]. 交通运输工程与信息学报，2020，18（1）：91-98.

（责任编辑：刘娉婷）