基于波长移相剪切干涉的准直波前重构技术
单小琴,韩志刚,朱日宏
(1.南京理工大学 紫金学院,江苏 南京 210046;2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)
引言
在干涉测量中,为保证测量精度需要校准干涉仪出射波前。检测光束准直性的方法[1]有自准直法、塔尔波特成像法、夏克-哈特曼法、五棱镜扫描法[2]、剪切干涉法[3-10]等。其中剪切干涉法以被检波前与其自身剪切波前之间在重叠范围内相干涉,从而评价被检波前本身的缺陷。横向剪切干涉法[3-9]采用共光路系统,干涉条纹稳定,环境适应性强,在波前测量领域得到了广泛的应用。传统提取剪切干涉条纹相位分布采用解析法[3],这种方法处理单帧干涉条纹,相位恢复精度较低。D.S.Mehta 等[4]提出双波长横向剪切干涉法实现波前及透射相位物体的测量。移相法能够精确测量干涉条纹的相位分布,H.Lee[5]等采用两组楔板实现正交方向上的横向剪切和移相。X.Guo[6]等提出了采用Savart 分光镜实现剪切,并采用空间移相方法提取剪切干涉条纹的相位分布。空间移相方法也被用于径向剪切干涉装置中[7]。改变激光器的波长亦可实现干涉条纹移相,从而精确提取相位分布[10-13]。G.Coppola[11]等提出了采用波长扫描法利用剪切干涉装置测量透射平板的厚度及折射率。本文提出了一种采用楔板及角锥棱镜实现剪切干涉测量干涉仪准直波前的方法,该方法利用干涉仪自身成像系统获取干涉条纹,并采用波长移相精确获取干涉条纹的相位分布。
1 原理
基于波长调谐的剪切干涉法重构干涉仪准直波前的系统结构如图1 所示,干涉仪出射波前分别被楔板的前后两个表面反射后,通过角锥棱镜返回在干涉仪CCD 上形成干涉条纹。

图1 基于波长调谐的剪切干涉法重构干涉仪准直波前的系统结构图Fig.1 Structure diagram of shear interferometry based on wavelength tuning to reconstruct interferometer collimated wavefront
如图2(a)所示,以干涉仪出射波面的中心为坐标原点建立xOy坐标系,干涉仪出射波前表示为W(x),x∈[a,d],波面的x∈[a,c]部分及x∈[b,d]部分分别经楔板的前后表面反射后形成波面WAC及WBD;这两组波面完全进入角锥棱镜并反射成为再由楔板反射后形成剪切波面

图2 测试光路Fig.2 Testing of optical path

其中CAC及CBD为常数,两者之间的错位量为s=b+da-c。于是光程差函数:
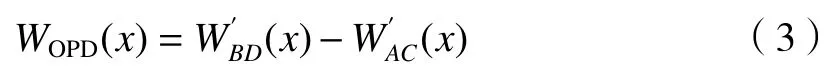

其中:Ibg(x) 为 背景光强;C(x)为调制度函数。由(1)~(4)式可知,干涉条纹的光强表达式中携带了干涉仪出射波前信息,可以通过恢复剪切干涉条纹的相位进而重构波前。
波前重构分两步完成,首先由波长移相方法提取剪切干涉图的相位分布,然后根据剪切量的大小分别采用积分法或待定系数法恢复干涉仪的出射波前。
1.1 基于波长调谐的剪切干涉图相位提取
对于波长可调谐的激光干涉条纹,Δλ的波长变化量引起的相位变化 Δφ为[8]

式中 λ0为中心波长。令时,定值的波长变化量产生的相位变化量亦是定值。采用四步相移法求解干涉条纹的相位分布,相位步进量定为 Δ φ=π/2,于是有其中的常数分量且当

采集4 幅相位间隔为π/2的干涉图,其光强分布分别为I1(x)、I2(x)、I3(x)及I4(x),从而解得剪切干涉条纹的光程差分布:
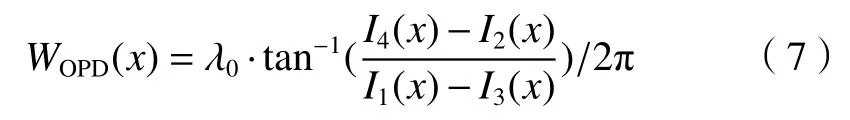
1.2 波前重构
1.2.1 积分法重构干涉仪出射波前
当剪切量很小,即b+d、a+c接近0 时,可采用积分法实现波前重构。光程差函数可以看成是W(x)的微分:

于是干涉仪出射波面为

1.2.2 待定系数法重构干涉仪出射波前
当剪切量较大时,(8)式并不成立。此时不妨设干涉仪出射的一维波面W(x)可用多项式表示,即:

其中n为0 到nMax间的整数,光程差函数WOPD(x)可写为

由上式可知WOPD(x)可以用x的nMax-1 阶函数表示,即:

建立(11)式、(12)式的相等关系,an可由系数bn及剪切量求得[14]:

将(13)式代入式(10)即可实现波前重构
2 实验
实验在100 mm 口径波长移相干涉仪上进行,该干涉仪为斐索型结构,波长调谐激光器采用Newfocus7004 型,波长变化范围是632.65 nm~632.97 nm。通过改变干涉仪扩束镜与准直物镜的相对位置来产生不同像差的准直波前,采用楔板与角锥产生剪切干涉条纹。图3 给出了沿光轴移动扩束镜时产生的三组剪切干涉干涉图,随着扩束镜的移动,剪切波面的倾斜量发生变化。设定产生剪切的两支光束的光程差常量为67 mm,采用波长移相方法求得图3 中L1L1'、L2L2'、L3L3'截线上的剪切波面,如图4 所示,扩束镜位于不同位置时的干涉仪出射波面如图5 所示,三组波面的峰谷值分别为3.22λ、2.10λ、0.83λ。可见不同倾斜量的剪切波面恢复得到的干涉仪出射波面的离焦量不同,倾斜得越厉害离焦量越大。
3 讨论
3.1 相对剪切比对波面重构精度的影响
相对剪切比Sr是指剪切量S与待检光束口径D的比值,定义剪切波面与干涉仪出射原波面的峰谷值之比为灵敏度Se,Sr影响了剪切干涉测量的灵敏度[3]。

图3 不同干涉仪出射波面的剪切干涉图Fig.3 Shear interferograms formed by different emergent wavefront of interferometer

图4 波长移相法恢复的剪切波面Fig.4 Shear wavefront retrieved by wavelength phaseshifting method
图6(a)仿真干涉仪出射波面W(x)=0.2·x2-0.4·x3+0.3·x4,x∈[-1,1],图6(b)给出了经过角锥剪切装置后,干涉仪得到的剪切比为0.2 的波面,图6(c)、(d)为分别采用积分法及待定系数法重构得到的波面与原波面的差值。可知剪切比为0.2时,待定系数法的重构效果比积分法好。

图5 由剪切波面恢复得到的干涉仪出射波面Fig.5 Interferometer emerging wavefront retrieved by shear wavefront

图6 剪切干涉波面重构仿真Fig.6 Simulation of shear wavefront reconstruction
表1 给出了不同剪切比Sr时,灵敏度值Se及分别采用积分法和待定系数法恢复得到的波面与原波面的差函数峰谷值Dint和Dco。可见随着相对剪切比的增加,灵敏度随之提高。对于积分法,随着相对剪切比的增加,波前重构精度降低;而对于待定系数法,相对剪切比对波面重构精度影响不大。
3.2 影响相对剪切比的因素
如图7 所示,在xOy坐标系内,楔板的前表面与y轴的夹角为α,楔板的楔角为φ,楔板的后表面与y轴夹角表示为α-φ。以角锥在主平面的交点R及R'到楔板前表面的距离L1及L2定位角锥的空间位置,角锥的口径为D,令,定义平行于y轴光线的光线L经楔板后表面反射后刚好经过角锥棱镜的R点,以楔板在边缘光线上的截线段h表示楔板的厚薄,这里不考虑楔板折射率的影响,即认为楔板的折射率为1。AC、BD及AB的大小可由(14)~(16)式表示:

表1 不同剪切比对波面灵敏度及波面重构精度的影响(仿真的干涉仪出射波面峰谷值为0.9λ)Table 1 Impact of different shear ratio on wavefront sensitivity and reconstruction accuracy (Simulated emerging wavefront peak-to-valley value of interferometer is 0.9λ)


图7 相对剪切比及其影响因素的关系Fig.7 Relation between relative shear ratio and its influence factors
于是

剪切干涉图的大小为

相对剪切比可由下式表示:

由(17)~(19)式可知,楔角、楔板的厚度、楔板的前表面与y轴的夹角及角锥的相对位置影响着相对剪切比。
3.2.1 楔角
图8 为仿真D=60 mm,α=50°,h=20 mm,L2=150 mm,β=60°时,楔角φ由0°变化至1°剪切干涉条纹的相对剪切比的变化情况,由图8 可知,相对剪切比随着楔角同步增大。当楔角为0°即楔板为平行平板时相对剪切比最小。需要指出的是当剪切板为平板时,干涉仪的像面上实际接受到四组波面,即干涉仪出射波面经剪切板前后表面反射至角锥并原路返回的两组波面分别再次由剪切板前后表面反射形成,它们两两相干,形成复杂的干涉条纹图案,如图9 所示。

图8 楔角对相对剪切比的影响Fig.8 Impact of wedge angle on relative shear ratio

图9 剪切板为平板时的干涉条纹Fig.9 Interference fringes obtained when shear plate is a flat plate
3.2.2 楔板的前表面与y轴的夹角α
图10 为仿真D=60 mm,φ=0.5°,h=1 mm,L2=150 mm,β=60°时,α由30°变化至70°剪切干涉条纹的相对剪切比的变化情况,由图可知,相对剪切比随着α的增大而减小。
3.2.3 楔板的厚度h
图11 为 仿 真D=60 mm,φ=0.5°,α=50°,L2=150 mm,β=60°时,h由15 mm 变化至25 mm 剪切干涉条纹的相对剪切比的变化情况,由图可知,相对剪切比随着h同步增大。

图10 α 对相对剪切比的影响Fig.10 Impact of α on relative shear ratio

图11h 对相对剪切比的影响Fig.11 Impact of h on relative shear ratio
3.2.4 角锥的相对位置
角锥相对于楔板的位置由L2及β决定。图12为 仿 真D=60 mm,h=20 mm,φ=0.5°,α=50°,L2=150 mm 时,β由50°变化至70°时剪切干涉条纹的相对剪切比的变化情况,由图可知,相对剪切比随着β的增大而增大。当β=60°不变,L2由100 mm变化至170 mm 时,相对剪切比随着L2的增大而增大。
3.3 估算光程差的常数分量
根据(6)式,采用波长调谐方式求解剪切干涉条纹需要估算形成剪切干涉条纹的两支光束的光程差WOPD(x)的常数分量以该常量为基础设定可调谐激光器的波长步进以实现移相量的标定[8]。不妨设干涉仪出射波面、角锥质量及楔板的面形皆理想以估算可以证明可 用下式表示:
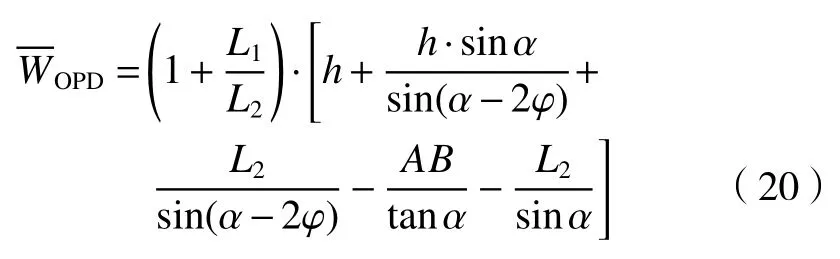
由此可见,估算光程差需要综合楔板的倾角、楔角及角锥的相对位置等综合因素。本文实验中,D=60 mm,φ=0.5°,α=50°,L2,L1分别约为250 mm,300 mm,h约为20 mm,估算光程差常量为67 mm。
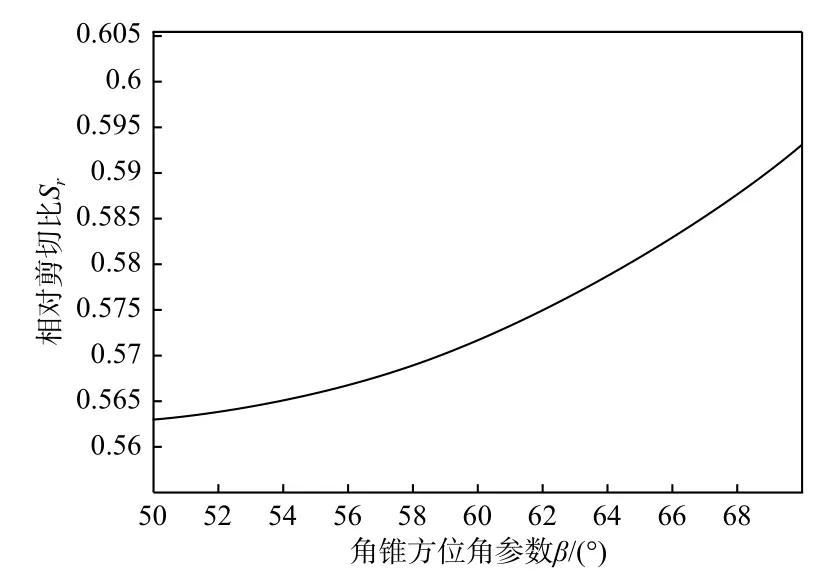
图12β 对相对剪切比的影响Fig.12 Impact of β on relative shear ratio

图13L2 对相对剪切比的影响Fig.13 Impact of L2 on relative shear ratio
4 结论
本文提出了基于波长调谐的横向剪切干涉法重构干涉仪准直波前方案,相比于传统的横向剪切干涉法,本文合理利用了角锥棱镜的反射特性,不需另外搭建成像系统即可形成剪切干涉条纹;利用波长移相方法实现剪切干涉图的相位提取,有效提高了波面的测量精度;分析相对剪切比对波面重构精度的影响;推导相对剪切比和其影响因素间的关系公式;给出波长移相中光程差常数分量的估算方法。该方法特别适合于测量波长移相式干涉仪的出射波前。
本文采用的实验装置中,楔板的前后表面面形及角锥质量都会对系统带来误差,影响测试结果;另外,大口径干涉仪的准直系统的检测可以采用本系统装置拼接实现,今后将在这两方面努力以改进我们的方法。

