振动测试齿轮箱轴承处动态载荷逆向识别研究
姜雨霆,赵松涛,吴 樾,霍肇波
(中国船舶重工集团公司第七O 三研究所,黑龙江哈尔滨 150078)
0 引言
齿轮传动是当前应用较为广泛的一种机械传动形式,与带传动等其他传动方式相比,具有传动比稳定、效率高、寿命长等优势,因此在传动系统中始终占有不可替代的位置。但是在齿轮箱正常运转过程中,齿轮系统受到内外部激励共同作用,其中内部激励是齿轮传动与其他一般传动机械的不同之处,由齿轮啮合过程中轮齿时变啮合刚度、轮齿传递误差以及啮入啮出冲击等因素组成的内部激励不可避免地产生了齿轮动态啮合力,这种动态激励力是引起齿轮振动和噪声的主要原因,而传递到轴承处的动态载荷作为齿轮箱箱体的输入激励,识别轴承处动态载荷更是对工程实际具有直接意义。
随着科学技术的不断发展,对于齿轮传动的小噪声、低振动提出了更加严格的要求,当前的技术手段已经难以满足这一要求,由于内部动态激励是齿轮传动振动噪声的主要原因,人们发现要处理齿轮箱振动噪声的问题应该从激励源入手,因此对于准确获得结构所受动态载荷激励的关注度也越来越高。动态载荷的识别方法有两种:直接测量法与间接识别法。直接测量法就是在载荷的传递路径上安装传感器,直接测量载荷相关参数。然而在许多实际工程中,由于技术和成本等因素限制,动态载荷无法直接测量,只能使用间接识别法,通过结构响应等数据逆向识别出结构所受的动态载荷。
动态载荷识别发展较晚,近年来理论以及软硬件的逐渐成熟使得人们取得越来越多的成果,智浩[1]等人通过对识别过程中精度影响因素的分析,提出利用计算机模拟方法选择响应测点以提高识别精度的方法;蔡元奇[2]等人提出了模态选取的概念与准则,经过大量算例证明,该准则与公式明显提高了动态载荷识别的成功率与精度;范永庆[3]等人推导了基于广义正交多项式的随机载荷识别模型,并且通过ANSYS 有限元法对复杂结构的载荷识别进行了验证,为复杂结构分布动载荷识别提供了一种新的理论和方法;郑海起[4]等人从理论上论证了相干修正可有效地抑制响应信号的测量噪声,并通过试验验证相干修正对提高识别冲击载荷精度的有效性;应广驰[5]等人通过测量涡轮增压器外壳上的可测量点的振动响应,反演出轴承座处的响应,从而为涡轮增压器的转子动力学研究提供了基础激励;王旌生[6]提出了在形成Mindlin 板单元质量阵时将剪应变看作等效的转角项计入系统的动能中,使Mindlin 板的质量阵中包含了剪切变形的影响,从而提高了结构频率的计算精度以及最终载荷识别的精度;赵玉成[7]等人应用小波正交算子的信息压缩性质,建立了能量相对集中的动力模型,得到了小波正交算子变化法,较好地处理了由于高阶模态信息贡献的截断对识别精度的影响问题。本文基于动载荷逆向识别理论,利用仿真软件由输入输出点之间的频响函数逆向识别出轴承处动态载荷,并且验证了动态载荷在啮合频率处的准确性。
1 逆向识别理论
目前对于动态载荷识别条件还有一定的限制,对系统的输入(待识别载荷)与输出(结构响应)关系应做以下假设:
(1)系统的输入激励与输出响应呈线性关系。
(2)系统的参数始终固定不变,不随时间改变。
(3)系统的可测响应完全由作用在系统上待识别的动载荷引起。
对于确定的系统结构响应:设待识别载荷数为Ni,实际测量响应点数目为N0,在满足系统线性假设条件下,动载荷矩阵为结构响应矩阵为的关系:

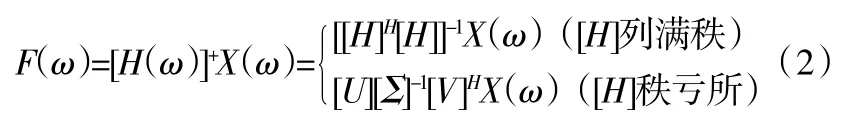
式(2)中,上角标“+”表示Moore-Penrose 广义逆,上角标“H”表示矩阵的共轭转置。U、V 分别为2 个酋矩阵,对角阵=diag(1,2,···,n),12···n0 为频响函数矩阵的所有奇异值,当rank(H)=nN 时,其N-n 个奇异值为零,即n+1=···=N=0对于不确定的系统随机响应:输入激励与输出响应可由谱密度函数表示如式(3):

当NiN0时,可由得到的响应自功率谱密度求解动载荷的自功率谱密度:

其中,i,j=1,2,...,N0。
当NiN0时,只有个独立方程,因此实际测量响应的点数应该满足
2 齿轮箱系统频响函数计算
齿轮产生的动态啮合力传递至轴承处进而引起齿轮箱箱体振动,本次使用的齿轮箱轴承为滑动轴承。由于滑动轴承在齿轮运行时产生油膜将轴抬起,传递路径较为复杂,再加上轴承处的动态激励同样可以直接反映出箱体的振动情况,所以选择识别齿轮箱轴承处动态激励。想要准确的识别出动态载荷,必须建立准确的与实际系统吻合的有限元模型,准确得到输入激励与输出响应之间的频响函数。系统振动情况与其固有特性有密切的关系,掌握了系统的固有特性可以为系统的振动噪声预估以及故障诊断提供重要依据,因此首先要对系统进行模态分析求解频响函数。
2.1 齿轮箱实体建模
首先使用专业三维软件Pro/E,按照齿轮箱实际尺寸建立齿轮箱箱体的三维模型。为了降低后期有限元网格划分的难度,加快计算速度,在不影响计算结果准确性的前提下,对齿轮箱模型进行修正与简化。在箱体中有很多圆角、倒角等特征,对箱体的振动特性影响很小,而在有限元网格划分中易造成局部网格质量不好,因此在建模过程中直接将这些细小特征删除,最终整体模型如图1所示。

图1 齿轮箱整体模型
2.2 齿轮箱有限元建模
在专业前处理软件Hypermesh 中,对三维模型进行有限元处理。本次箱体与支撑架均采用10 节点4 面体的Solid187 单元进行网格划分,首先在模型表面划分出二维面网格,检查网格质量合格后,生成三维体网格。理论上,网格尺寸越小,网格越密集、仿真精度越高,但是随着网格增多,计算耗费的时间也会大大增加,因此根据齿轮箱实际大小以及经验,将有限元网格设置为15 mm,得到齿轮箱箱体共有64 238 个节点、229 969 个单元,支撑架共有39 619 个节点、147 108 个单元(图2、图3)。
2.3 模态计算
在有限元仿真中,除了自身参数与实际要尽量一致外,系统的边界条件与实际情况的吻合程度也将直接影响最终结果的准确性,因此在对系统进行模态分析之前要根据齿轮箱实际装配情况在软件中对齿轮箱箱体和支撑架添加边界约束。本次使用LMS 公司的Virtual lab 软件对边界条件进行设置,使用Nastran求解器进行模态计算,对于支撑架与地面的连接,在软件中建立Bush 单元连接来模拟支撑架与地面间的螺栓连接,因为支撑架四角有额外安装压板固定,所以设置四角的Bush 单元的x、y、z方向刚度均为1e 10 Nm,其余6 个底面Bush 单元的x、y、z 方向刚度设为5e8 Nm;对于箱体与支撑架之间的连接,同样建立Bush 单元,其x、y、z 的3 个方向刚度均为5e8 Nm。

图2 箱体有限元模型

图3 支撑架有限元模型
另外,通过对齿轮箱传动系统建模,在Pro/E 中可以计算得到两根齿轮轴的质量分别为532 kg 和104 kg,依据两根轴的质量在轴承孔中心点设置集中质量与齿轮箱轴承孔相连接,最终处理后的模型以及前两阶振型如图46 所示,前六阶固有频率及振型如表1 所示。
得到齿轮箱的固有频域与振型后,就可以根据模态参数计算齿轮箱的频响函数特性,其中12 个轴承载荷到1#测点3 个方向的频响函数如图79 所示。
3 轴承动态激励逆向识别与验证
上文对齿轮箱系统进行了有限元模态分析,得到了相应两点之间的频响函数,进而可以由测试点的响应数据逆推出输入动载荷。
3.1 振动响应试验

图4 处理后模型

图5 第一阶模态振型
为了得到齿轮箱的振动响应数据,需要进行响应测试试验。本次试验使用kistler 公司的三向加速度传感器,Brüel&Kjær 公司的12通道信号采集器与测试软件。总共在箱体表面布置11 个测点,1#~10#测点的响应数据用于动载荷识别,11#测点不参与动态载荷逆向识别计算而是留作载荷识别验证用(图10、图11)。本次振动响应试验的工况设定为转速2000 r/min,扭矩6880 Nm,图12图14 为BK 软件测得的1#测点3 个方向的加速度响应频域图谱。
3.2 轴承处动态激励逆向识别
本次使用Virtual Lab 软件逆向求解轴承处动载荷,取试验中的前10 个测点作为动载荷逆向识别的输入点,把BK 软件在响应测试中得到测点的真实响应幅值与相位输入到对应点上,以齿轮箱的4 个轴承孔作为载荷的输出点。响应测试试验的工况为2000 r/min,已知输入轴小齿轮齿数为37,对应啮合频率为1233 Hz 左右。由于电机转速波动,未达到理论转速,因此振动测试与仿真得到的振动加速度峰值均在1200 Hz处,主要关注动态载荷与箱体响应在啮合频率附近的幅值。图15~图17 为仿真逆向识别出3#轴承横、轴、垂3个方向的动态载荷频域图。

图6 第二阶模态振型

表1 前六阶固有频率与振型
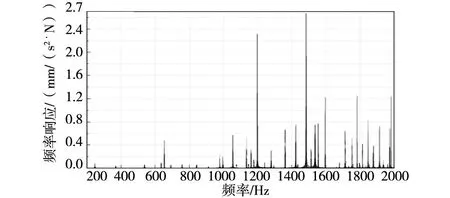
图7 载荷输入点到1#测点横向频响函数
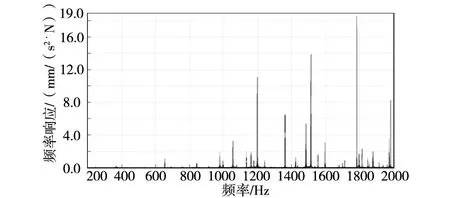
图8 载荷输入点到1#测点垂向频响函数

图9 载荷输入点到1#测点轴向频响函数
最终识别出4 个轴承处在3 个方向的动载荷在1233 Hz 附近的幅值如表2 所示。

图10 测点位置

图11 传感器布置

图12 1#测点横向振动加速度

图13 1#测点垂向振动加速度
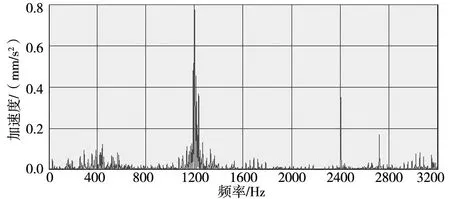
图14 1#轴点横向振动加速度

图15 3#轴承横向动态载荷
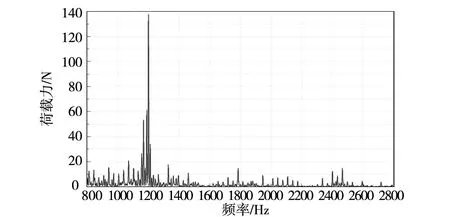
图16 3#轴承垂向动态载荷
3.3 仿真结果分析与验证
为了验证识别出动态载荷的准确度,将识别出的动态力重新代入模型,对应施加在齿轮箱轴承孔中心的集中质量点处,作为输入激励来计算未参加载荷逆向识别的11#测点的响应,仿真计算得到11#测点横、垂、轴3 个方向的振动响应如图18图20 所示。

图17 3#轴承轴向动态载荷
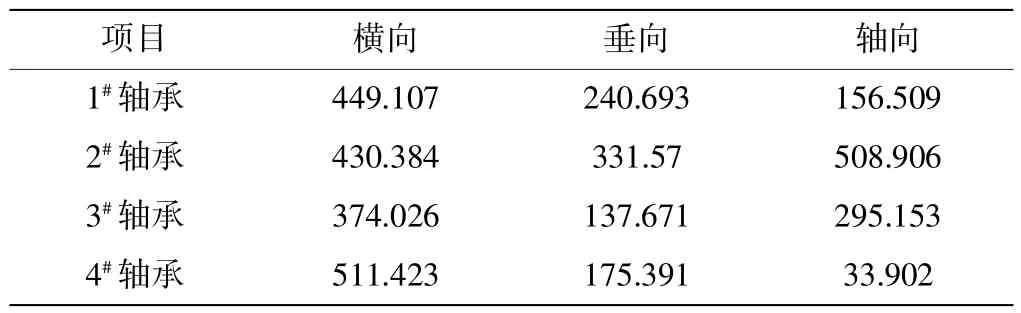
表2 轴承处动载荷在啮频处幅值

图18 11#测点横向振动加速度

图19 11#测点垂向振动加速度
最终,以11#测点的响应数据作为验证依据,将仿真计算出的响应数据与响应试验测得的响应数据进行对比。可以发现,在横向上,仿真得到的振动加速度在1200 Hz 处对应峰值为1.575 m/s2,而响应测试得到的振动加速度在1200 Hz 处对应峰值为1.42 m/s2,相对误差为11%;在垂向上,仿真得到的振动加速度在1200 Hz 处对应峰值为0.688 mm/s2,而响应测试得到的振动加速度在1200 Hz 处对应峰值为0.893 mm/s2,相对误差为23%;在轴向上,仿真得到的振动加速度在1200 Hz 处对应峰值为4.961 m/s2,而响应测试得到的振动加速度在1200 Hz 处对应峰值为4.13 m/s2,相对误差为20%。

图20 11#测点轴向振动加速度
通过对比,齿轮箱箱体响应测点的仿真结果与试验结果在啮合频率处的幅值比较接近,相对误差均约20%,二者结果具有较好的一致性,证明逆向识别出的轴承处动态载荷是具有参考价值的。振动加速度响应在600 Hz 处有峰值,这是因为在测试齿轮箱前端有一个增速齿轮箱、增速箱将其啮合频率激励沿功率流传递到了所研究的减速齿轮箱所导致的。
4 结论
本研究结合了模态分析、结构振动响应分析,联合运用了Pro/E、Hypermesh 以及Virtual lab 软件,先对齿轮箱系统进行三维建模,将模型导入Hypermesh 软件中建立有限元模型,Virtual lab 中添加边界条件计算模态参数,以频响函数为依据,成功由振动试验测量的箱体表面振动响应逆向求解得到一定工况下轴承处动态载荷。将计算得到的动态载荷重新作为输入,仿真出其他测点的振动响应,通过仿真结果与试验结果的对比,最终得到在啮合频率处,用逆向识别出的轴承处动态载荷计算得到的箱体响应幅值与试验测得测点的响应幅值误差较小,验证了这种动态载荷逆向识别方法有一定实用性。尽管识别出的轴承处动态载荷中含有内外部激励耦合的成分,但仍能从中找到齿轮啮合产生的动态激励,并以此来预估齿轮啮合作用下齿轮箱系统的振动特性,为齿轮系统设计、齿轮箱故障诊断以及振动控制提供有效参考依据。

