以能力为导向的大学数学思想方法的教学研究

侯江霞 刘德民

摘  要：文章讨论了在大学数学课程教学中的若干思想方法与能力培养方面的问题。首先探讨了大学数学课程教学中的三种思想方法：逼近的思想与方法，由简入繁思想方法和化繁为简的思想与方法;再次讨论了五种基本能力的培养：具体问题数学化的能力、定性描述与定量表述的能力、数学对象具体化的能力、数学理论应用推广的能力及数学语言的使用能力。

关键词：大学数学;数学思想和方法;数学能力

中图分类号：G642        文献标志码：A         文章编号：2096-000X（2020）07-0114-04

Abstract： In this paper， we talk about some methods of mathematical thoughts and the development of mathematical abilities. The approximation idea， the methods from simple to complicate and from complicated to simple are three methods on teaching advanced mathematics. The abilities of transforming concrete problems to mathematical problems， qualitative description and quantitative description， make the pure mathematical object to special problems， application of mathematical theory and mathematical notation.

Keywords： Advanced Mathematics; methods of mathematical thoughts; Mathematical abilities

引言

眾所周知，现代高等教育的四大职能是教育教学、科学研究、服务社会和文化传承，而促进人的全面发展是高等教育的终极目的。在现代高等教育的实施过程中，也即人才的培养过程中，尤其是理工科人才的培养方面，数学知识与理论的教学是重中之重。正如李大潜院士所述[1]：“数学是一种科学的语言和工具，是众多科学与技术的基础，而且是一门博大精深的科学，更是一种先进的文化，在人类认识世界和改造世界的过程中一直发挥着重要的作用与影响。”数学教育和学习的目的正是通过数学的学习，理解数学的重要性，领会到数学的精神实质和思想方法，提高并具备将数学应用于解决实际问题的能力。

大学阶段的理工科数学教学主要以高等数学、线性代数为基础，结合工程数学及复变函数等内容而展开;文科专业主要以一元函数微积分和概率统计初步知识为基础进行讲授。在具体的课程学习阶段，由于课程内容、师资力量与教学水平、学生人数与数学基础、以及教学软、硬件设施等多方面的原因，使得大学数学课程的教学并不总能收到满意的效果。甚至于很多大学生仅能做到会求导数、会算积分、会求解简单的常微分方程等简单的操作，不理解数学的思想与方法，更不能在其它课程与学科的学习中起到促进作用。因此，大学数学课程的有效讲授与学习至关重要，尤其是高等数学课程的教学。

一、三种重要的数学思想与方法

作为数学学科的教育与科研工作者，我们深切的体会到数学课程的思想与方法的重要性，一旦领会了思想与方法，便能举一反三，融会贯通。结合多年的教学实践，这里首先谈一谈高等数学课程教学中的三点思想与方法，即逼近的思想与方法、由简入繁的思想与方法，以及化繁为简的思想与方法。

（一）逼近的思想与方法

“逼近”，简单的说就是逐步靠近，包含近似与逐步细化两个内容，它既是解决问题的思想之一，也是解决问题的方法之一。“逼近”可以起到化抽象为具体、化繁为简、化难为易等作用，它可以有效的促进人脑对抽象知识的理解和推广，提高人的认知能力。

纵观数学课程的内容，可以发现逼近无处不在，甚至可以毫不夸张的说，没有逼近就没有现代微积分理论及其发展应用。尤其在大学数学课程的内容中，以下几类逼近思想与方法尤为突出[2]。

1. 以直代曲（或以平代曲），即以平直的线（或者曲面）代替曲线（或曲面）。

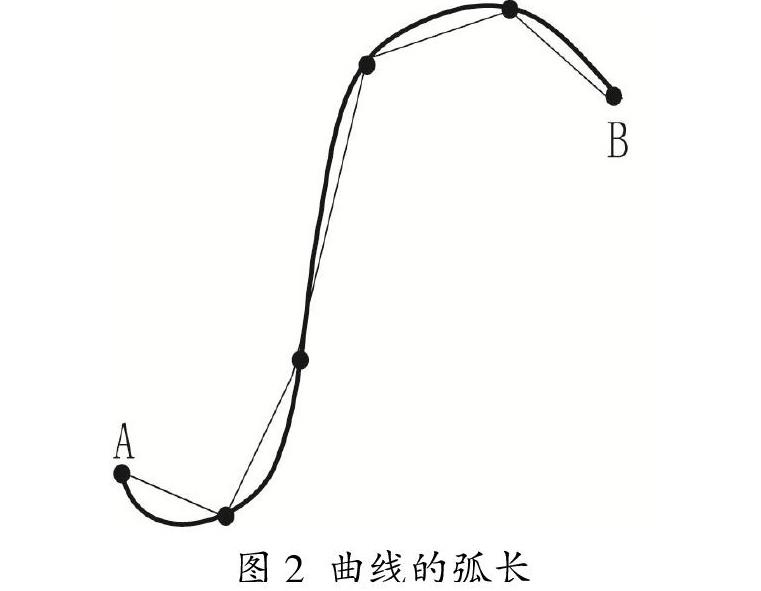
例如，小学时学习圆面积的计算公式S=？仔r2，其求法可如图1所示。将圆的面积归结为若干个扇形面积的和，进一步利用直边三角形代替扇形得到每个扇形的近似面积，通过对圆弧的进一步细分，得到圆面积的公式。这里用到了最简单的逼近“以直代曲”，该方法在大学数学课程中比比皆是。例如，再求曲线的弧长（如图2），曲线所围图形的面积（如图3），曲顶六面体的体积（如图4）等等。

2. 以匀代变，即以均匀的量代替变化的量。

例如在学习变力（x，y）沿着由点A至点B的曲线l做功时，如图5所示，通常是先将曲线l划分为很多段（以直代曲），在适当的假设下可以认为在每一段上力（x，y）的变化不大，从而可以某一点的力（？孜，？浊）作为该段上力

（x，y）的近似值（以匀代变）。例如沿着弧   所做的功近似等于（？孜，？浊）。

3. 以熟代生，即以熟悉的数学形式代替陌生的数学形式。

例如，无穷小量的等价替换。简单的线性函数x及幂函数xi，i=2，3，...，的表达形式及几何直观是大家熟知的，从而当x→0时，通过无穷小等价替换可以得到sinx～x，tanx～x，cosx～1-x2，～1x等，利用这些关系可以更好地了解这些函数的局部性质。又如指数函数ex和多项式函数是学生所熟悉的。虽然求ex的函数值是困难的，但是学习了泰勒展式之后，知道ex可以用熟悉的多项式函数来近似，ex=1+x++…++…，x∈（-∞，+∞），困难的问题也会变得容易解决了。

（二）由简入繁的思想与方法

“由简入繁”即由简单的数学对象过渡到复杂的数学对象;或由简单的数学理论过渡到复杂的数学理论;或由一个数学分支过渡到另外的数学分支等。“由简入繁”同样既是研究问题的思想之一，也是研究问题的方法之一。“由简入繁思想与方法”可以建立良好的知识架构和思维规律，并形成完备的知识体系。

结合大学数学课程的内容，我们可以看到很多“由简入繁”的例子。例如，在高等数学教学内容的安排上，由一元函数的极限、连续、导数，微分、积分等过渡到多元函数的相应内容;由数列、函数到数项级数、函数项级数、幂级数、三角级数等;由点、向量、直线、平面到曲线、曲面、体等;由数量函数到向量函数、场论等。

在学习无穷级数时，已知有限项的和比较容易，对于级数这类无穷多项和的数学对象就变的困难多。将级数求和转化为部分和序列的极限问题，即先求有限项的和，再求这有限项和的极限。部分和序列有极限，则级数收敛，此时通常可以用一个解析的关系表达级数的和。相对于级数的复杂形式，级数和的解析形式就简单很多，如

（三）化繁为简的思想与方法

“化繁为简”是将待解决问题逐步划分为几个或一系列简单的问题加以解决的思想和方法。“化繁为简”是一个将问题拆分、知识点逐步细化、知识点综合应用、知识点相互关联形成系统的一个过程和方法。通过“化繁为简”可以有效地促進把握知识点、加深对知识点间内部关联、构建一个系统的知识体系及解决大问题的能力。

“化繁为简”通常包含细化知识点和综合知识点的两个过程。例如，要研究一个函数f（x）在区间（a，b]上的连续性。首先来进行知识点的逐步细化。利用函数在一个区间连续的定义，则对函数f（x）在区间（a，b]上的连续性研究转化为函数f（x）在区间（a，b]内任一点x的连续性问题，进一步转化为研究函数f（x）该点x处的左连续、右连续及函数在该点的取值问题，再进一步转化为函数f（x）在该点x处的左极限、右极限及函数定义的问题。再次来看知识点的综合应用。通过上述细化过程，发现如果能够知道函数

f（x）在任一点x∈（a，b）处的左极限、右极限、函数的定义，以及f（x）在区间左端点a处的右极限及定义、f（x）在区间右端点b处的左极限和定义，则函数f（x）在区间（a，b]上的连续性就得到解决。

二、五种能力的培养

以上我们讨论了高等数学课程教学中的三种重要思想与方法，接下来谈一谈在教学中五种能力的培养。

（一）具体问题数学化的能力

具体问题数学化简单的讲就是将生产实践中的具体问题用数学的形式表达出来。通常需要人为的引入相关的变量、函数、限定条件，建立相应的图表、公式、表达式等，将已知的量、条件与未知的量等用特定的数字数学符号表达出来。

例如，《庄子·天下》记录了庄子的好朋友、名家人物惠施的命题之“一尺之棰，日取其半，万世不竭”， 其含义是：一尺长的杆，每天截去它的一半，千秋万代也截不完。数学上我们来看怎么解释，假设杆的长度为1个标准单位，通过引入变量n代表第n天，以及an表示第n天所取的杆的长度，则容易得到，

所以命题是在说

按照等比级数的求和，上述关系显然是正确的，从而惠施的命题是成立的。

（二）定性描述与定量演绎的能力

以定量代替定性，即以一个确定的量的关系去表达一个性质。

例如函数f（x）在一点x=x0的极限定义。定性描述为当x趋近于x0时，对应的函数值f（x）无限趋近于某个确定的值A，就称函数f（x）在点x=x0处的极限为A。定性描述总是很容易理解，但是却不便于演绎推理。借助于？着-？啄语言的定量关系，则问题变得容易解决。

（三）数学对象具体化的能力

数学对象具体化即是将数学上的字母、数字、函数、矩阵等具体的数学对象转化为生产实际中具体研究对象。高等数学课程中会采用很多的字母、数字、符号等数学对象，而这些数学对象通常都是可以和生产实际中的具体对象相对应的。

例如在区间[a，b]上的一个函数f（x）。可以将f（x）看做一个化学反应从时刻a变化到时刻b的反应物浓度，此时x是时间变量;也可以将f（x）看做是从河道的一端a到河道的另外一端b之间河道每一点处的宽度或深度等，此时x 是空间变量。一个矩阵A=0 12 0可以看做是一个线性变换x1=yy1=2x的变换矩阵;也可以看做是两个机场I、II间的航班情况，如下图：

（四）数学理论应用推广的能力

数学理论应用推广能力主要包含两点，第一点是将简单问题上的数学理论推广到复杂问题上;第二是指将数学理论推广应用到具体的实际问题。

关于第一点，例如学习了一阶导数的求法，则二阶导数就是对一阶导函数再求导;n阶导数就是对n-1阶导函数再求导。再比如讲完一元函数的积分，则二元函数的积分可以先将其中一个被积变量看做固定，而关于另外一个被积变量做一元函数的积分，所得积分结果再关于刚才假设固定的变量做积分，这个思想很容易推广到三重积分及更高维数的积分概念当中。

关于第二点，更多的体现在利用数学的定理、性质去解决生产实际问题。例如利用极值理论解决用料最省体积最大问题;利用隐函数定理解决非线性方程的求解问题等。

（五）数学语言的使用能力

数学语言分为符号语言、文字语言、图表语言和公式语言等，是表达数学思想的专门语言，具有抽象性、准确性、简约性和形式化等特点[3，4，5]。有效地使用数学语言，能够促进知识点的掌握、改善数学思维、增强数学表达和交流、提高学习的兴趣与能力、提升理论与实际的转化能力等。

符号语言是在人类数学思维长期发展过程中不断使用并凝练下来的一种语言表达形式，往往具有确定的意义与通用的使用规则。2011年颁布的《义务教育数学课程标准》将符号意识作为10个核心素养之一[6]。从中小学的初等数学介绍的“+”、“-”、“×”、“÷”，取对数符号“log”到高等数学介绍的导数符号“” ，“”，积分符号“∫”、以及“？坌”，“？埚”等符号，在大学数学教学中更要有意加强学生对符号的写法、意义的理解，并鼓励使用。

数学中的文字语言是指数学理论中经过对自然语言加工改造后具有精确的意义及严谨地使用规则的一类语义单位。例如“区域”、 “极限”、“微分”、“洛必达法则”、“积分中值定理”等。图表语言指包含一定数学信息的各种图、表。例如“柱面”、“单叶双曲面”、“马鞍面”、“函数导数表”、“一元函数积分表”等。公式语言是指包含特殊的关系及明确意义的表达式。如欧拉公式：eix=cos（x）+isin（x）;格林公式、高斯公式等。

在《教育部关于一流本科课程建设的实施意见》中提到“课程是人才培养的核心要素，课程质量直接决定人才培养质量”。大学数学课程的学习既是为学好专业课打基础，又是培养学生发现问题、分析问题、解决问题能力的重要时期。对教师而言，在教学过程中除了要讲好必要的知识点，还要注重以能力为导向，将数学思想和方法融会贯通，杜绝单纯知识传递，才能真正将大学数学课程起到培养创新型、复合型人才的作用。

参考文献：

[1]李大潜.漫谈大学数学教学的目标与方法[J].中国大学教学，2009（1）：7-10.

[2]同济大学数学系.高等数学（上册、下册）[M].高等教育出版社，2007.

[3]鲍建生.数学语言的教学[J].数学通报，1992（10）：2-2.

[4]邵光华，刘明海.数学语言及其教学研究[J].课程·教材·教法，2005（2）：36-41+35.

[5]A·斯托利亚尔.数学教育学[M].丁尔升，等，译.北京;人民教育出版社，1984.

[6]朱立明，马云鹏.学生数学符号意识PORE评价框架的构建[J].数学教育学报，2016，25（1）：84-87.