深度学习,让理性思维点亮数学课堂
陈国梁
【摘 要】深度学习,就是摒弃传统的以“满堂灌”为主的教学模式,突出学生主体,侧重学生思维能力的发展的新型教学。将其运用到初中数学教学中,不仅能激发兴趣、调动思维,还能引导主动探究,让学生在合作交流中理性思考,由此促进核心素养的发展,帮助其拓宽解题思路,逐步形成高效的学习方式。本文将结合实际围绕深度学习从导入、探究、合作及总结方面探究具体策略。
【关键词】初中数学;深度学习;策略
在新课改背景下,如何促进学生探究,帮助其形成高效的学习策略是我们共同关注的问题。对此,就要借助深度学习展开,利用问题探究引导思考,在分析、总结中培养学生迁移解决问题的能力,以此促进完整教学体系与结构的搭建。在这一过程中,要时刻关注学生思维品质与关键能力的提升,让其在数学課堂上体会探知的乐趣,下面我就结合实例从不同方面作具体阐述。
一、导入——多元设计,激发兴趣
“良好的开端是成功的一半”,有效的导入不仅能活跃课堂,调动氛围,还能激发思维,让学生对学习内容充满兴趣。基于这一点,在设计教学时,就要加强重视,在传统基础上创新设计,争取在短时间内吸引学生,帮助其融入到课堂中,展开深度思考。
在新课授课中,大多数教师将心思花在重点讲解上,忽略了导入部分,以致于方式和手段都比较单一。常见的做法是问题导入,即运用一两个问题作为引入,缺乏深入的思考与有效设计,使整个“开场白”都索然无味。特级教师于漪说过:“课的第一锤要敲在学生的心灵上,激发他们思维的火花,或像磁铁一样把学生牢牢吸引住”。学生被充分调动了,才会主动融入到课堂中,针对问题展开积极思考,无形中激发其求知欲、挑战欲及参与欲。基于这一目标,在设计时,就要根据每节课的教学目标与任务,科学设计导入方案,根据学生兴趣丰富导入手段。除了最常见的直接导入外,还可运用挂图、模型导入、多媒体、图片视觉化导入。这些导入方法,在教学《几何图形初步》时就可运用,将学习内容直观呈现,促进学生感性认知,就能调动其探究兴趣,为后续展开做好铺垫。或者,在教学《勾股定理》、《一次函数》等较难且有知识背景的内容时,就可设疑导入、借助生活情境导入或者实践导入等,以此激发学生,让其在明确重难点的同时尽快进入学习状态,全神贯注地参与课堂。在这一过程中,需要注意的是,要根据教学内容充分调动思维,让学生逐步深入,以此完善知识体系。
好的课不仅要突出重点,帮助学生明确探究目标,更要善于调动其兴趣,让其在逐步深入中掌握要点,形成学习方法。长此以往,学生对于数学机会有崭新认识,并在兴趣调动下主动参与,充分发散思维,挖掘学科内涵。
二、探究——变式拓展,发散思维
在传统教学中,大多数教师专注教材,力求让学生听懂、会做,这种做法无可非议。然而,要想让学生真正掌握,就要借助变式,让其在典型问题的针对性思考中多角度、多层次、多方面地认识,由此促进理解,就能在无形中提升自学能力。
高质量的数学题目很多,学生不可能一下子全部做完,也不可能全都会做,那么如何促进其掌握有效的解题方法?这就需要抓住典型题目变式,借此激发学生深层思考,让其在探究中提升思维。以这一题为例:在△ABC中,∠2=62°,∠1=20°,∠2=35°。求∠BDC的度数。这一题难度不大,学生很快就解决了,这时对于这样一道典型题目,就不能草草过去,而要抓住条件中的重点进行变式,主要有以下几种,在呈现时可根据难度安排顺序:
变式1 在△ABC中,∠2=62°,BD和CD分别是∠ABC和∠ACB的平分线,求∠BDC的度数。
变式2 在△ABC中,∠A=n°,BD和CD分别是∠ABC和∠ACB的平分线,请用含n的代数式表示∠BDC的度数。
变式3 在△ABC中,∠A=n°,∠ABC的平分线和∠ACB的外角平分线相交于点D,请用含n的代数式表示∠BDC的度数。
变式4 在△ABC中,∠A=n°,∠ABC的外角平分线和∠ACB的外角平分线相交于点D,请用含n的代数式表示∠BDC的度数。
通过这样的变式,将问题中的某些条件或结论构造出来,就可将典型题目由“特殊”转化为“一般”,以此帮助学生掌握相应的提醒,在实际解决中体悟问题解决的一般方法,逐步体会到品尝成功的乐趣,进而产生对数学探究更浓厚的兴趣。
三、合作——探究解题,培养能力
“数学教学是数学思维活动的教学”,在数学课堂上,要想提升学生素养,就要充分调动其思维,让其在问题引导下自主思考、发现、解决,以构建深度课堂。在这一过程中,要鼓励学生合作探究,共同探讨,以深入挖掘,抓住问题本质。
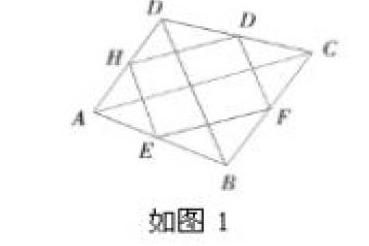
在以往的教学中,对于不同难度的问题,大多数教师总习惯讲解,在学生思维无法突破时,将自身思考代替其探究。这种做法很大程度上局限了学生思维,使其在面对问题时难以发散,最终造成能力上的缺失。对此,就要借助问题引导,营造合作探究的氛围,鼓励学生大胆说出自己的想法。以“三角形的中位线”教学为例,其中中点四边形是重点,对此就可呈现相关题目引导:如图1,E、F、G、H分别是四边形ABCD各边的中点,请你求证:1.四边形EFGH是平行四边形;2.四边形ABCD满足什么条件,可使EFGH成为特殊的平行四边形?对于这一问题,第一小题难度较小,学生稍作思考便能运用定理解决。第二小题答案较多,随着思考的深入,学生的探究难度会增加,这时就可稍作引导,借助“支架”启发:1.当AC=BD时,四边形EFGH成为什么?2.请你添加一个条件,使得EFGH成为___?3.你能否再添加一个条件,使得EFGH成为正方形?在这一环节,就先让学生独立思考,在完成一定内容后,带着想法与疑惑进入合作,借助团体的力量解决问题。这时,作为课堂引导者,就要融入到学生中,围绕重难点展开,以此发散思维,促进问题解决。
借助这一过程,能帮助学生内化知识,提升数学思维,在不断深入中体悟到要点内涵,由此促进掌握,在后续训练中能灵活运用。需要注意的是,对于一部分后进生,要加强指导,在关键处点拨,为其顺利探究提供帮助,以增强学习信心。
四、总结——小结归理,提升素养
课堂小结是初中数学教学一个十分重要的环节,不仅是课堂的组成部分,更是教学艺术的呈现。因此,在此环节一定要加强重视,在课堂上注意运用适当方法,引导学生进行课堂小结,促进其对研究过程的把握,由此掌握探究方法,有效地完善知识。
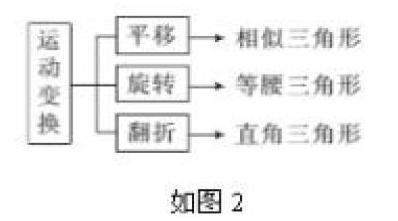
在教学中,优化课堂小结的设计不仅是让教学更完善,也是对整个课堂学习成果的一次巩固。基于这一点,在教学中,就要加强重视,采取不同方法总结,以此调动思维,促进学生对要点的回顾与二次掌握,及时查漏补缺,完善体系。在教学“图形与变换(1)——平移、旋转、翻折”时,虽然内容不难,但是为了促进学生了解并掌握,就可借助思维导图总结,如图2。实施时,就可先让学生自主总结:今天你学到了什么?能否依次说出关键词?由此,学生便回顾,得到了“平移”、“旋转”及“翻折”,在这一基础上课适当细化,让其依次对应不同三角形。在这一环节,可穿插讨论环节,以小组为单位引导交流,让学生将知识点与模型连接,透过现象看到本质,依次完善知识构建,为其后续思考奠定基础。在这一过程中,要加强与学生的互动交流,在其反馈中了解到课堂教学的不足,以此作及时的补充,并在之后的训练中完善。
可见,课堂小结的合理运用能架起知识点与数学模型、解题方法之间的桥梁,借助问题激发学生思考,让其透过现象加深对数学知识本质的理解,促使教学达到事半功倍的效果,所谓“课堂尽,思未了”。
总之,深度学习的开展是优化当下初中数学教学的有效途径,将其落实到教学中,不仅能培养学生理性思维,还能提升其解决问题的能力。在這一过程中,要深刻体悟数学课堂是发展学生思维、提升数学素养的主阵地,要为学生长久深远的发展努力。
【参考文献】
[1]谭必钟.基于深度学习的初中数学教学策略探讨[J].考试周刊,2017,(89):108
[2]邹冰涵,金爱冬.基于深度学习的初中数学课堂教学策略[J].时代教育,2018,(13):121
(江苏省苏州市吴江区桃源中学,江苏 苏州 215200)

