动态空间网络中的黑洞模式挖掘算法*
谭胜昔,贾金萍,赵 斌,吉根林
(南京师范大学计算机科学与技术学院,江苏 南京 210023)
1 引言
随着全球定位技术、无线通讯技术的持续发展,以及移动终端设备的广泛普及,大规模移动数据的获取已经成为可能。按照数据来源的不同,常见的移动数据包括手机终端定位与通讯记录、公交刷卡记录、GPS的轨迹数据、社交网络签到数据等[1]。此类数据记录了空间、时间、方向、速度和POI(Point of Interest)等方面的信息。这为人类移动模式研究带来了前所未有的机遇和挑战。通过分析和挖掘移动数据可以为现代城市的交通管理、疾病防控、城市规划和旅游推荐等应用领域提供有力的方法指导和决策支持。
人类移动模式研究[2 - 5]是移动数据挖掘中的一个热点问题,其研究任务是发现移动对象群体的运动模式和活动规律,如城市人群的通勤活动、游行集会和交通拥堵等。按照研究类型的不同,人类移动模式研究分为面向群体的研究和面向地理空间的研究[6]。典型的面向群体的移动模式包括成群模式(Flock)[7]、护航模式(Convoy)[8]、蜂群模式(Swarm)[9]和聚合模式(Gathering)[10]等。此类研究从运动形态的视角出发分析与挖掘群体移动的规律性,可以发现具有相同运动形态的移动对象群体。但是,挖掘方法中不涉及地理空间信息,因而无法发现地理空间中区域间的移动模式。面向地理空间的研究从地理空间的视角研究人类移动模式,弥补了这一不足。2014年,Kim等人[11]利用空间上聚集的地铁站点研究区域间的移动交互模式。Chen等人[12]采用出租车的OD(Origin to Destination)数据研究城市中功能区域间的移动交互模式。Liang等人[13]在ACM 顶级会议SIGSPATIAL上提出了基于空间网络模型的黑洞模式,研究地理空间中人类群体的聚集移动模式,并将此研究工作定义为空间网络中的子图发现问题。
黑洞模式的研究工作是人类移动模式研究的标志性成果,但在移动模式的演化建模方面存在局限性。黑洞模式定义在空间网络模型上,该网络含有地理空间的结点(路口、拐点等)及其连接的边,但不包含任何时间信息,因而无法反映移动群体在地理空间中随时间的分布变化,对于在地理空间中移动对象群体的运动演化趋势研究存在局限性。以“上海踩踏事件”[14]为例,在外滩附近的道路网络中人群经过一段逐渐汇聚的过程形成了广场区域的大规模拥堵。现有的黑洞模式通过空间网络的子图发现方法可以发现路网中人群聚集的街区,但无法对地理空间中移动群体的持续变化状态进行建模,因而也就无法跟踪、发现人群的汇聚趋势,甚至预测可能引发的潜在踩踏风险。
基于上述分析,本文将研究具有时间演化特性的黑洞模式。新模式在保留原定义的群体规模性和空间区域性的同时,将增加时间演化特性,使之有效反映移动对象群体在空间网络中随时间变化的分布情况,这将有助于揭示地理空间中群体性的移动规律。但是,具有时间演化特性的黑洞模式挖掘研究会面临2方面挑战。
(1)定义新的空间网络模型。原有的黑洞模式是基于空间网络模型定义的,而该网络模型中包含地理空间和网络流量2方面信息。新黑洞模式需要增加时间演化性,这就要求空间网络中包含随时间变化的流量信息,即需要提出动态的空间网络模型。
(2)在动态空间网络中如何提升黑洞模式的挖掘效率。Liang等人[13]将黑洞模式挖掘定义为空间网络中的子图发现问题,经过证明,此问题是NP完全问题。而当前研究的动态空间网络流量数据随时间变化不断增加、持续累积,数据规模巨大,因而从动态空间网络中挖掘黑洞模式依然需要巨大的计算代价。
为了应对上述挑战,本文提出具有时间演化特性的动态空间网络模型,基于此模型定义新的黑洞模式,并提出相应的挖掘算法。本文提出的动态空间网络将边权重属性定义为权重的时间序列,用以反映群体移动行为在空间网络上随时间的流量变化。相应地,本文提出的黑洞模式在满足群体规模和空间区域2方面要求的前提下,还需要满足流量变化的约束要求。为了提升模式挖掘算法的效率,本文设计了基于时空划分的候选模式剪枝算法,有效降低了挖掘算法在时空维中的搜索代价。最后,基于真实数据的实验结果表明了本文提出的黑洞模式及其挖掘算法的有效性和可行性。
2 问题定义
在地理空间中的人群聚集行为具有时间持续性、空间区域性和群体规模性。结合上述特性,本节提出动态空间网络和黑洞模式的定义,并且提出动态空间网络中的黑洞模式挖掘问题。
定义1(动态空间网络) 1个动态空间网络记作G=(V,E),与G相关的时间区间记作T,V={v1,…,vn}表示顶点集合,E={e1,…,em}表示边的集合,T={t1,…,tk}表示由单位时间段构成的序列,ti表示T中的第i个单位时间段,|T|为时间序列中单位时间段的个数。任意边e∈E的流量属性表示为时间序列形式,记作{f(e,t1),…,f(e,tk)}。
定义2(进/出流量) 边e的进流量指在单位时间段内进入e的移动对象数量,记作fin(e,t)=∑e′∈(E-e)f(e′,e,t),其中f(e′,e,t)表示在时间段t内从边e′进入边e的移动对象数。同理,边e的出流量记作fout(e,t)=∑e′∈(E-e)f(e,e′,t)。令边集E′为E的1个子集,则E′的入流量表示在单位时间段内从其他边进入边集E′的移动对象总数,记作fin(E′,t)=∑e∈E′,e′∈(E-E′)f(e′,e,t)。同理,E′的出流量记作fout(E′,t)=∑e∈E′,e′∈(E-E′)f(e,e′,t)。
定义3(净流量) 净流量表示在单位时间段内进入边或边集流量的净值。如果进流量小于出流量,则净流量为负值。边e在单位时间段t内的净流量记作fa(e,t)=fin(e,t)-fout(e,t)。同理,边集E的净流量记作fa(E,t)=fin(E,t)-fout(E,t)。
定义4(黑洞模式) 用S=(V,E)表示G的1个子图,其中S.V和S.E分别为G.V和G.E的子集,任意边e∈S.E的权重序列为{fa(e,ts),…,fa(e,te)},T′={ts,ts+1,…,te}是T的子序列,表示黑洞模式S持续的时间,ts和te分别表示模式的起止单位时间段。S的净流量记作S.fa=∑t∈T′fa(S.E,t)。若S满足下列条件,则称S是1个黑洞模式:
(1)S满足连通性;
(2)|T′|≥θ;
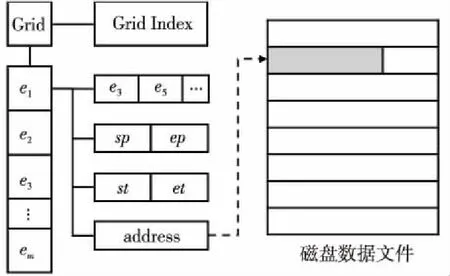
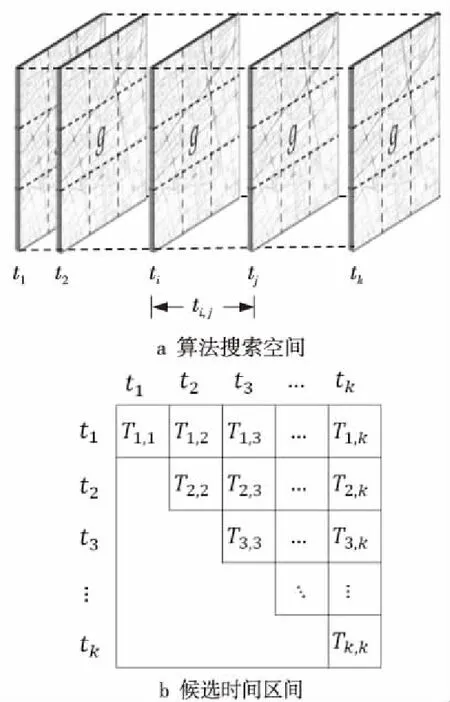
(3)MBB(S) (4)S.fa/|T′|≥δ。 其中,θ称作模式的时间阈值,它规定了聚集事件的持续过程需要满足一定时长;d称作空间阈值,它规定对聚集事件的识别在空间上需要足够精确,其中MBB指子图在空间上最小外包矩形的对角线长度;δ称作流量阈值,它规定所检测的聚集事件需要满足一定的群体流量规模,且对于持续时间较长的聚集事件,其流量规模也应较大。 问题定义给定1个动态空间网络G、时间阈值θ、空间阈值d和流量阈值δ,黑洞模式挖掘算法的目标是找到G中符合上述定义的黑洞模式集合BH={S1,S2,…,Sn},其中BH满足下列条件: (1)对于∀Si∈BH,1≤i≤n,S满足定义4; (2)对于∀Si∈(G-BH),Si不满足定义4; (3)∀Sa,Sb∈BH(Sa≠Sb),Sa.E∩Sb.E≠∅和Sa.T′∩Sb.T′≠∅不能同时成立。 实际上,同一聚集事件在网络中可能对应多种子图组合,列举出所有的子图会造成挖掘结果的高度冗余,不利于结果分析与展示。此外,黑洞模式挖掘本质上是1种基于密度的子图搜索问题,这被证明是1个NP完全问题[15]。如果列举所有的候选子图并对其逐一验证,该方法的计算复杂度为指数级。因此,在动态空间网络中,放弃挖掘黑洞模式的准确结果,而选择挖掘黑洞模式的近似结果是较为合理的。 黑洞模式挖掘的基本框架包含2部分:动态空间网络构建和黑洞模式挖掘,如图1所示。 Figure 1 Framework of black hole pattern mining algorithm图1 黑洞模式挖掘算法框架 (1)动态空间网络构建。 首先从路网数据中提取路段和路口数据,根据其拓扑关系生成空间网络。接着对轨迹数据和空间网络数据进行路网匹配,确定轨迹数据与路网中路段的对应关系,从而统计在不同时间段内各路段的流量信息,生成对应边上的动态权重,最终完成动态空间网络的构建。 (2)黑洞模式挖掘。 该部分负责对动态空间网络数据进行挖掘,生成黑洞模式结果集。算法在时空维上将网络划分为若干时空区间,并采用剪枝算法将部分流量稀疏无法形成黑洞的区间予以排除,从而降低算法计算代价,最终在候选的时空区间内搜索黑洞模式。为了避免结果集的冗余,在搜索黑洞模式的同时,更新动态空间网络数据以及候选时空区间,防止对网络的重复搜索。 本文将城市路段作为空间网络中的空间实体,将路段与路段之间的邻接关系对应为空间网络中实体的拓扑关系。原始的路网数据为空间矢量数据,不具备空间网络的图结构性质。因此,首先需要对路网数据进行预处理,从中提取路段和路口的信息,包括标识和空间位置属性,并根据其邻接关系构建空间网络。 动态空间网络的构建需要计算路段上随时间变化的流量值。而轨迹数据是移动对象在二维空间中运动形成的位置点序列,和城市道路空间没有直接的映射关系。因此,为了能够计算动态空间网络边的权重序列,需要通过路网匹配操作[16],将原始轨迹数据中的位置点对应到各路段上,接着对不同时刻下路段上的移动对象数进行统计,生成各边上的权重序列。 性质1给定路段e和时间段t,假设在t的开始时刻路段e上的移动对象数为p,在结束时刻e上的移动对象数为q,则路段e在时间段t内的净流量fa(e,t)=q-p。 证明根据净流量定义,有q=p+fin(e,t)-fout(e,t),变换可得q-p=fin(e,t)-fout(e,t)=fa(e,t)。故性质1得证。 □ 根据定义,净流量的计算需要统计各移动对象在不同路段上的进出情况,计算量较大。而由性质1,在计算单位时间段内路段上的净流量时,只需要直接计算起止时刻该路段上的移动对象数的差值即可,从而避免了净流量统计的高代价计算。 模式挖掘的过程中需要频繁访问动态空间网络数据。然而随着数据的不断累积,动态空间网络数据的规模不断增大,这导致模式挖掘过程中无法将数据全部加载在内存中,而只能将数据保存在磁盘上,造成数据访问效率低下。为了加快数据的查询效率,提高算法性能,本文针对存放在磁盘上的动态空间网络数据设计相应的索引。如图2所示,利用空间网格索引将各边分配到对应的网格单元,以提高对边数据的空间查询效率。对索引中的每一条边存储其拓扑关系和时空属性,用邻接表记录其邻边集合,sp和ep分别表示其起止端点的空间信息,st和et指其动态权重的起止单位时间段信息。数据以边为单位存储在磁盘上,每一个数据单元记录该边的权重序列,并将其磁盘偏移量记录在索引中,方便快速寻址。 Figure 2 Index of dynamic spatial network data图2 动态空间网络数据索引 黑洞模式挖掘本质上是一种图数据中的子图发现问题,其时间复杂度随着数据规模的增大呈指数级增长。由于动态空间网络数据随着时间增长不断累积,其数据量在时间维度上规模巨大,若不经优化,直接对其展开黑洞模式的挖掘将耗费大量的时间。黑洞模式对应了网络中流量相对密集的子图结构。现实中移动对象分布的不均匀性导致网络中的流量分布也是不均匀的,由此网络中部分流量稀疏的时空区间必然无法形成黑洞模式,可直接予以排除,不需要参与黑洞的检测。因此,为了压缩模式挖掘的搜索空间,本文在空间和时间2个维度将动态空间网络划分为若干时空区间,并筛选出流量相对密集的时空区间作为候选参与黑洞模式的检测。黑洞模式算法伪代码如算法1所示。 算法1黑洞模式挖掘算法 输入:动态空间网络G,时间区间T,时间阈值θ,空间阈值d,流量阈值δ。 输出:黑洞模式集合BH。 1.BH←∅; 2.GS←SpatialPart(G,d);/*空间维划分后生成候选区域集合*/ 3. for eachg∈GSdo 4.TS←TemporalPart(T,θ);/*进行时间段划分,得到不同时间段的候选区域*/ 5.FilterByF(TS);//初步过滤算法 6.FilterByH(TS);/*结合流量持续性要求进一步过滤算法*/ 7. whileTS≠∅ do 8.Ti,j←MaxUB(TS);//上界最大候选 9.BH′←BHExpansion(g,Ti,j);/*搜索黑洞模式*/ 10.BH←BH∪BH′; 11.Update(g,TS);//更新候选区间 12. end while 13. end for 首先讨论在空间维上的划分方式。由于黑洞模式挖掘最终将在候选时空区间内进行,因此对搜索空间的划分需要确保划分边界不会影响挖掘结果的完整性。受传统黑洞模式研究工作的启发,本文利用网格结构对动态空间网络进行空间维的划分。如图3所示,假设模式的空间阈值为d,用边长为d的方格对网络进行空间维上的划分,gab表示行列号分别为a和b的方格,gab.E表示方格内的边集合,则有如下性质。 性质2给定一个黑洞模式S和方格gab,若S.E∩gab.E≠∅,则必有S.E⊂AR(gab),其中AR(gab)定义为由满足|i-a|≤1,|j-b|≤1的所有方格gij组成的区域,称作网格gab的邻域,邻域内的边集记为AR(gab).E。 Figure 3 Schematic diagram of spatial division图3 空间划分示意图 性质2表明,针对任意方格内网络数据的黑洞模式挖掘,其搜索边界是方格对应的邻域。因而,通过空间维的数据划分,挖掘任务被分解为各网格及其邻域内的黑洞模式挖掘问题。以针对方格g的黑洞模式挖掘为例,如图4a所示,挖掘算法的搜索空间在空间维上是AR(g),在时间维上是T。由于黑洞模式的持续时长并不固定,因此需要在T时域上搜索满足阈值的任意长度的黑洞模式,令Ti,j={ti,ti+1,…,tj},如图4b中矩阵所示,假设模式的时间阈值为θ,则{Ti,j|1≤i≤j≤k,j-i≥θ}是所有需要搜索的候选时间区间。 Figure 4 Searching space of black hole pattern mining图4 黑洞模式挖掘搜索空间 随着数据的积累,动态空间网络数据在时间维上的规模较大,导致算法搜索空间扩大。由于现实中同一地区内不可能长时间保持人流量的高速增长,因此AR(g)中网络的净流量在T上通常是稀疏的。对于某些流量值过于稀疏而不可能形成黑洞模式的时间区间,考虑通过适当的筛选手段予以排除。下文以候选时间区间Ti,j={ti,ti+1,…,tj}为例,讨论在不同流量规模下的取舍。 性质3子图S的净流量等于对应边集在其时域内的净流量之和,即S.fa=∑t∈S.T′,e∈S.Efa(e,t)。 证明根据定义2和定义3可作如下推导: S.fa=∑t∈S.T′fa(S.E,t)= ∑t∈S.T′(fin(S.E,t)-fout(S.E,t))= ∑t∈S.T′(∑e∈S.Efin(e,t)-∑e∈S.Efout(e,t))= ∑t∈S.T′(∑e∈S.E(fin(e,t)-fout(e,t)))= ∑t∈S.T′(∑e∈S.Efa(e,t))= ∑t∈S.T′,e∈S.Efa(e,t) 故性质3得证。 □ 综上所述,对于方格g中的任意候选时间区间Ti,j而言,Fi,j和Hi,j分别为其子图净流量的2个上界,Fi,j误差较大但方便计算,Hi,j过滤效果更好但计算代价较高。因此,考虑先利用Fi,j筛选如图4b中所有的候选时间区间 ,再利用Hi,j对经过初步筛选的候选时间区间作进一步的筛选。经过时间区间的筛选,最终对剩下的候选时间区间采用下文中的搜索算法挖掘满足阈值要求的黑洞模式。 由于动态空间网络中流量的物理含义相同,故黑洞模式的搜索可继续沿用传统黑洞模式的启发式搜索策略[13]。每次从候选集中选择流量上界最大的时间区间Ti,j展开搜索。首先对方格中的每条边e计算Ti,j时间区间内的净流量和fa(e,Ti,j)。取方格g内净流量和最大的1条边构成初始子图S,其中S.T′=Ti,j,随后采用迭代的方式对子图进行扩张。在每次迭代中,取当前子图S的邻边作为候选边集合,对候选边集合中的每1条边e进行打分,取分值最高的边扩展当前子图,打分策略如下所示: 其中,Δ指的是S在加入边e之后对角线的变化值,即Δ=MBB(S+e)-MBB(S),为了便于描述,其中S+e为S中加入边e后生成的新子图的简单表示。得分为-∞或MBB(S+e)超出空间阈值的边不予扩展,当没有候选边可用于扩展时,迭代结束。若此时的子图S满足S.fa/|S.T′|≥δ,则将其作为结果输出,同时将S所涉及的边从候选数据集中删除,防止重复检测,同时刷新候选时间区间流量值。按上述算法重复搜索黑洞模式,直到候选集为空。 为了验证基于动态空间网络的黑洞模式及其挖掘算法的有效性和高效性,本文使用真实的GPS轨迹数据和路网数据进行实验。实验环境为Windows 10操作系统,处理器为Intel Core i5,主频3.20 GHz,内存12 GB,硬盘容量500 GB,硬盘转速为7 200转/秒。 实验数据为上海市路网数据和出租车轨迹数据。路网由286 591条路段和262 764个路口构成。轨迹数据是2015年4月2日上海市13 518辆出租车形成的时空轨迹。基于2类数据构建出动态空间网络,数据大小为18.5 GB。 实验将从模式定义的有效性和挖掘算法的效率2个方面对基于动态空间网络的黑洞模式挖掘算法进行评估。 在有效性方面,本文以空间网络的黑洞模式挖掘算法[12]为比较对象。将空间网络的黑洞模式简称为BH-SN(Black Hole in Spatial Network),将本文提出的基于动态空间网络的黑洞模式简称为BH-DSN(Black Hole in Dynamic Spatial Network)。由于2种模式在群体规模性和空间区域性方面的约束要求相同,因而本文从挖掘结果的重合情况及其时长2方面进行对比。如果2种挖掘算法的结果重合数量越多,则说明BH-DSN和BH-SN一样有效,如果在高重合的情况下BH-DSN比BH-SN得到更多的结果,则说明BH-DSN比BH-SN更有效。另一方面,比较重合结果的时长情况,即相同参数设置下BH-DSN结果的时间区间与BH-SN结果的时间区间存在包含、分离和相交3种情况。如果在重合结果中,BH-DSN模式的时间区间包含BH-SN模式的时间区间比较多,则说明BH-DSN模式挖掘算法能发现时长更完整的聚集过程。 在算法效率实验部分,主要对比基于网格划分的黑洞模式挖掘算法BHPM(Black Hole Pattern Mining)和对搜索空间进行剪枝的改进算法BHPM*两者的性能。效率实验分2组进行:第1组实验比较两者在不同规模数据集下的运行时间;第2组实验比较了2个算法在不同参数下的运行时间,包括BH-DSN模式定义中的时间阈值、空间阈值和流量阈值3个参数。 有效性分析的参数设置如下。BH-DSN的参数设置为:时间阈值θ=3,空间阈值d=150 m,流量阈值δ=5,动态空间网络的流量汇总时间间隔为1/2/3/4/5 min(分5组进行)。由于BH-SN模式基于流量汇总时间段内的静态流量进行定义,为了保证公平性,其流量阈值为θ*δ=15,空间阈值同为150 m,空间网络的流量汇总时间间隔为3/6/9/12/15 min。输入数据的规模为4月2日一整天的数据集。在上述时间间隔设置下,2种模式的检测结果均对应最小持续时长为3/6/9/12/15 min的聚集事件,且根据定义,2种模式所检测到的聚集事件在单位时空区间内的流量值是相同的,即检测的目标是对等的。 表1描述了2种模式挖掘结果的重合情况,重合数指BH-SN模式的挖掘结果和BH-DSN挖掘结果在空间上重合的数量,其中,若2种模式的MBB在空间上相交,则说明2者相互邻近,判定为重合。从表1可以看出,在不同的汇总时间间隔下,BH-DSN模式的挖掘结果几乎均能完全覆盖BH-SN模式的挖掘结果,不仅如此,BH-DSN模式的挖掘结果在数量上更多,而根据定义,2者的挖掘目标是对等的,因此进一步,BH-DSN模式能检测到更多BH-SN模式无法检测到的聚集事件。之所以出现这样的差异,是因为BH-SN针对空间网络中的静态流量进行定义,对于聚集事件的检测效果取决于流量汇总的时间区间。例如,若某1聚集事件形成过程的前半段和后半段被划分到不同的黑洞模式挖掘批次,则有可能因流量没有达到阈值而无法被检测。而BH-DSN模式基于动态流量而定义,检测范围覆盖任意时间区间,且群体规模随时间跨度的不同而调整,因此能对发生在任何时间区间内的聚集事件进行准确检测。实验结果表明,本文提出的黑洞模式能对区域中的聚集事件进行更有效的检测。 Table 1 Repetition of mining results表1 挖掘结果重合情况 表2分析了2种模式重合结果的平均时长以及时间区间的包含情况。其中,包含(相交、相离)比例指BH-DSN模式的时间区间对BH-SN模式呈现包含(相交、相离)关系的数量占比。结果表明,BH-DSN模式挖掘结果的时间长度比BH-DSN模式的更长,且在时间区间上普遍包含BH-DSN模式的。这是由于BH-DSN模式的定义更加灵活,能对任意时长的聚集事件进行检测,而传统的BH-SN模式的检测效果取决于空间网络流量汇总的时间间隔。实验结果表明,BH-DSN模式能对聚集事件的过程进行更完整的检测。 Table 2 Comparison of mining time表2 挖掘时长对比 本节对本文提出的算法进行效率方面的实验分析。首先进行第1组实验,分析在不同数据规模下BHPM和BHPM*的性能表现。单次实验的输入数据开始时间均为2015年4月2日上午6点,动态空间网格数据的流量汇总时间间隔均为1 min,通过设置不同的结束时间,可以控制输入数据的规模大小。算法参数设置如下:时间阈值θ=3,空间阈值d=100 m,流量阈值δ=3。 从图5可以看出,在数据规模相同的情况下,BHPM*算法的运行时间显著低于不经过优化的BHPM算法,并且随着数据规模的增大,2者的运行时间差异也越来越大。 Figure 5 Algorithm execution time varies with data scale图5 算法执行时间随数据规模的变化 第2组效率实验对比2个算法在不同参数设置情况下的运行时间。实验采用控制变量的方法进行,即在改变其中1项参数的情况下,保持另外2项参数不变,测试数据的规模均为2 h,流量汇总时间间隔为1 min。默认的参数设置如下:时间阈值θ=3,空间阈值d=100 m,流量阈值δ=3。 Figure 6 Algorithm execution time varies with time threshold图6 算法执行时间随时间阈值的变化 Figure 7 Algorithm execution time varies with space threshold图7 算法执行时间随空间阈值的变化 Figure 8 Algorithm execution time varies with flow threshold图8 算法执行时间随流量阈值的变化 图6~图8分别对比了算法执行时间在不同时间阈值、空间阈值和流量阈值下的变化情况。可以看出,相比于原始算法,BHPM*算法的性能有数量级的提升。其中,算法的执行时间随着时间阈值和流量阈值的增大而缩短,这是因为这2个阈值的增大代表着对模式的时间和流量规模的要求提高,产生的候选集较少。同理,随着空间阈值的提高,黑洞模式的候选集越多,算法执行时间随之增加。 本文提出了一种基于动态空间网络的黑洞模式,用于城市群体聚集事件的识别和检测。该模式与现有研究相比,在时空维上表现出更加准确的识别效果。由于动态空间网络数据随时间不断累积而规模巨大,为了提高模式挖掘效率,本文利用动态空间网络流量分布不均的特点对黑洞模式挖掘搜索空间剪枝,提高算法性能。通过实验分析验证了基于动态空间网络的黑洞模式在有效性方面的优势,并通过对比黑洞模式挖掘算法及其改进算法的运行时间,验证了本文提出的改进算法的优化效果。3 算法设计
3.1 黑洞模式挖掘算法框架

3.2 动态空间网络构建
3.3 黑洞模式挖掘算法

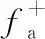
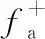
4 实验与分析
4.1 实验设置
4.2 评价方法
4.3 算法有效性


4.4 算法效率




5 结束语

