基于人机交互式图割的目标快速提取*
徐秋平
(武警工程大学信息工程学院,陕西 西安 710086)
1 引言
目标提取是指利用灰度、颜色、纹理、形状等信息从图像中提取出感兴趣的目标,它是图像工程中目标表达、特征提取和参数测量的基础,进而使得更高层的图像分析和理解成为可能。人们利用各种数学理论和模型工具,研究出了错综复杂的目标提取方法。基于能量最小化理论,学者们提出了融合高层视觉线索和先验知识的技术框架,给出了参数形式[1]、几何形式[2]及组合优化形式[3,4]的活动轮廓模型。
利用图割理论解决机器视觉问题是近年来组合优化领域发展起来的一个新兴热点分支[5]。其创新之处在于以人为本的交互方式[3]、新颖独特的纠错设计[4]、结合各种先验知识的学习机制[6 - 9]、全局最优的求解能力[10,11]以及统一的问题解决框架[12]。图割将图像映射为1个s-t网络,像素对应网络节点,像素特征对应边权值,割的容量对应能量函数,对s-t网络进行最小代价切割得到机器视觉问题的解。
就目标提取问题而言,基于图割理论主要有2类基本解决框架:一类是以GrabCut算法[13]为代表的基于区域信息的提取方法。GrabCut以高斯混和模型GMM(Gaussian Mixture Model)表征目标/背景,在GMM参数学习估计过程中用可进化的迭代算法来完成能量最小化。该方法要求概率模型有良好的表征和区分目标/背景的能力,概率模型参数的确定和海量计算是其面对的2大难题;另一类是以基于图割的活动轮廓线GCBAC(Graph Cuts Based Active Contours)算法[14]为代表的基于边缘信息的提取方法。GCBAC以边缘梯度信息来表征目标边界,从给定初始轮廓线的邻域开始,迭代切割,更新邻域,最终将活动轮廓线收敛至目标边界。该类方法采用迭代局部寻优策略,难以避免陷入局部极值。

Figure 1 Roadmap of graph cut theory图1 图割理论技术路线
国内外研究人员就运用图割理论解决目标提取问题进行了广泛深入的研究。文献[8]在Graph Cuts中加入先验信息。文献[15]提出一种新的查找最优路径算法,提高了Graph Cuts目标提取质量。文献[16]提出Lazy Snapping方法,在分割前利用K-means算法将图像分成小块,将各小块作为s-t网络中的节点,降低算法复杂度。文献[17]提出了归一化割Ncut(Normalized cut),利用轮廓特征和纹理特征构建全局最小化代价函数,生成规则超像素,但图像边界保持不完整,计算量较大,处理大图像时速度慢。文献[18]采用支持向量机SVM(Support Vector Machine)分类器对每个像素进行后验概率标记,然后使用基于图割的概率传播方法来自动提取复杂遥感图像中的路网。文献[19]综合地震中毁损建筑形状、边、角的特征,构造能量函数,采用最大期望EM(Expectation Maximization)算法设定分类阈值,实现了高分遥感图像中毁损建筑的检测。文献[20]以Lazy Snapping[16]为框架,引入多尺度分水岭进行预分割,实现了基于区域的羊体图像分割。文献[21]采用交互分水岭算法对图像进行区域划分,重新构造能量函数和s-t网络,实现了生猪目标的快速准确分割。文献[22]以interactive graph cuts[3]为框架,采用高斯混合模型计算t-link权值,去除人工标记环节,实现遥感图像中水体自提取。文献[23]先用归一化割[17]方法完成冠层初始分割,以全局最大值代替局部最大值,实现单木精确探测。
后期对前期提取结果中的局部错误进行提示反馈并能够纠正,是算法进一步提高准确率的重要举措,也是基于图割进行目标提取的特色机制。图割理论因其特有的s-t网络结构而能够便捷地进行后期纠错。如,GCBAC[14]算法通过在目标边界添加硬约束点,约束活动轮廓线必须经过所添硬约束点来实现纠错;Interactive graph cuts[3]、GrabCut[13]和OneCut[24]等算法则通过在错误区域添加目标或背景种子实现纠错;文献[25]则通过人工指定纠错域,对其重新切割实现纠错。
人机交互式方法本质在于人与机器的整合,既融入了人独有的智力判断,又利用了机器强大的计算能力,使得目标提取速度更快、精度更高、可操控性更强。人机交互式目标提取方法在诸如医学目标获取、运动目标识别等领域有着广泛应用。
本文以基于边缘信息的图割提取框架为基础,对活动轮廓线迭代过程进行深入研究分析,重新构造能量函数与s-t网络,消除前后重叠,避免重复切割,并在提取后期辅以手自结合的纠错手段,寻求一种人机交互方便快捷,纠错方式有效完备,目标提取快速准确的提取算法。
2 技术路线
图割理论的技术路线是将目标提取问题转化为能量最小化问题,并运用组合优化技术获取能量函数的全局最优解。如图1所示,首先将目标提取问题归结为将图像像素P标为L={目标,背景}的f:P→L的标号问题,进而通过构造能量函数,将其转换为1个能量最小化的优化问题;然后构造s-t网络,将问题转化为1个网络最小割问题;最后根据最大流-最小割定理将问题转化为网络最大流问题。目前已有诸多经典成熟算法可在多项式时间内对网络最大流问题求得最优解。

Figure 2 Algorithmic design图2 算法设计
3 算法设计
本文算法基本设计如图2a所示,在目标边界附近,以人机交互方式输入1条封闭的多边形折线作为初始活动轮廓线。以其为基准,向两侧膨胀固定宽度得到1个环状域。运用图割理论,对该环状域构造s-t网络并进行最小代价切割得到1条新的活动轮廓线。由此经过若干次迭代,最终活动轮廓线变形至目标边界。
4 算法实现
在图像中,目标边界像素颜色值的剧烈变化是图像重要的基本特征,因此,可通过构造能量函数对目标边界的这一重要基本特征加以表达,并映射成s-t网络,通过最小代价切割来识别目标边界。
4.1 构造能量函数
在s-t网络中,若2个相邻节点对应的像素处于非边缘处,则二者间的边权值应较大,从而将二者切断的代价较高;反之,若2个相邻节点对应的像素处于边缘处(如1个是目标中的像素,另1个是背景中的像素),则二者间的边权值应较小,使得将二者切断开的代价较低。本文算法通过式(1)来表征具备上述2个特性的2个像素间的RGB值间的距离,采用式(2)设计s-t网络边权值wij,进而构造实现目标提取的能量函数。
Cij=‖Ii-Ij‖2
(1)
其中,Ii和Ij分别为节点i,j所对应像素颜色值(一般可取RGB值)。
(2)
其中,E为s-t网络边集。
4.2 构造s-t网络
当前环状域覆盖部分目标边界段后,需要构造合适的s-t网络,使得最小代价切割后,所得活动轮廓线能够经过这些覆盖的目标边界段。
以环状域外边界作为s-t网络源点s,内边界作为s-t网络汇点t,环状域内部每个像素映射为1个网络节点,以8邻域方式连接相邻节点,边权值为式(2)中的wij。对于与源点s或汇点t相连的内部节点,其权值为该节点所对应的像素与环状域外边界或内边界中所有相连接的像素的权值累加。
在以上述方法构造的s-t网络中,边权值大小与边的粗细正相关,目标边界两侧节点所对应的像素颜色值变化剧烈,所连接的边的权值较小,目标边界经过的所有边的权值累加也为最小。因此,目标提取问题最终转化为对该s-t网络进行最小代价切割,也就是对s-t网络进行切割,得到曲线f,曲线所经过的边的权值之和为该条曲线所对应的切割代价cost(f),切割代价最小的曲线对应目标边界,即::
(3)
5 算法完善
第3节通过构造能量函数和映射s-t网络,得到了具备目标提取功能的初步算法。在具体实现中,继续对初步算法进行改进,得到1个效率更高、交互方式更为完整的完善算法:
(1)重新构造s-t网络,提高算法提取效率。初步算法的邻域是1个以固定宽度向活动轮廓线两侧膨胀的环状邻域(以下称“双侧定宽域”),如图2b所示,本文将其改造为单侧向内膨胀、宽度可变的单侧变宽域(以下称“单侧变宽域”),大幅减少切割s-t网络的时间消耗,显著提高算法效率。
(2)引入后期纠错机制,凸显人机交互特色。目标提取的复杂性使得算法难以做到完全正确提取目标,本文巧妙沿用前期目标提取算法框架,给出了一种方便快捷、安全导向、手自结合的纠错方法。
5.1 设计单侧变宽域
(1)定宽域向变宽域的改进。
当前活动轮廓线经过若干次变形后,部分活动轮廓线到达了目标边界(以下称“已达段”);部分尚未到达目标边界(以下称“未达段”)。随着迭代的进行,已达段越来越多,未达段越来越少,最终未达段消失,已达段构成目标边界。
对已达段,在之后的迭代中,由于已经到达目标边界,不再变化,显然之后对其膨胀生成的邻域进行切割已无必要。但是,初步算法没有对当前活动轮廓线进行“已达”与“未达”的分类,仍会对已达段所在邻域进行切割。随着活动轮廓线逼近目标边界,已达段越来越多,这种无效切割问题愈显突出。
因此,可对当前活动轮廓线进行“已达”与“未达”分类,迭代时仅对未达段所在邻域进行切割,从而避免无效切割,提高算法效率。要实现该思路,有2个问题要解决:一是如何判定已达段,二是如何避免对已达段所在邻域反复切割。
①已达段的判定。
已达段已经到达目标边界,因而其具有不再变化的性质。理论上,可将当前活动轮廓线Ci与前1次活动轮廓线Ci-1进行比较,其不变部分判定为已达段。但是,实际上Ci与Ci-1中可能会存在少数位置暂时不变但并未真正到达目标边界的像素,这些像素一旦被误判为“已达”后就会被错误固定下来,造成算法失败。
为避免上述问题,本文通过取连续n次(n≥2)活动轮廓线进行比较来减少误判。n值越大,误判可能性越低,但会推迟部分曲线段的“已达”判定。在实践中,n=3时即可在减少误判的同时对活动轮廓线进行有效分类。
②避免反复切割已达段。
如何实现不再对已达段所在邻域切割?考虑到不调整算法基本架构,本文采取的策略仍是统一进行切割,通过将已达段所在邻域宽度压缩为零来实现对已达段所在邻域切割代价为0,从而来等价实现避免反复切割。具体步骤为:对未达段,仍向两侧膨胀,形成固定宽度的邻域;对已达段,向外侧膨胀1个像素,形成宽度为0的轮廓线邻域。由此将原来宽度固定的环状邻域变为宽度可变的0-1脉冲式邻域。
在将上述变宽域映射成s-t网络时,变宽域内外边界分别对应s-t网络单一的源点、汇点,已达段的零宽度邻域被映射到单一的源点、汇点中,从而实现了零代价切割且切割后已达段位置保持不变。
(2)双侧域向单侧域的改进。
如图3所示,为便于观察分析,假设活动轮廓线邻域宽度为d,初始轮廓线与目标边界相距4d,二者之间为白色匀质区域。1次切割后,当前活动轮廓线变形到其邻域内边界,即活动轮廓线以每次d/2的速度逼近目标边界。
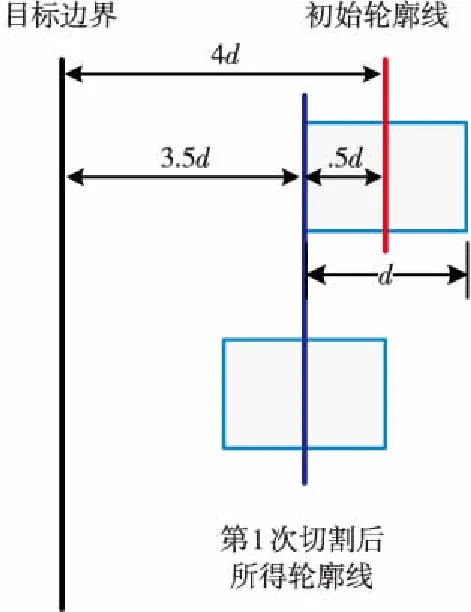
Figure 3 Improvement of neighborhood from bilateral-way to unilateral-way图3 双侧域向单侧域的改进
分析上述迭代切割过程可以发现:先后2条活动轮廓线所生成的邻域有d/2宽度的位置重叠,这种重叠会造成先后2次对该d/2宽重叠区域进行重复切割。在上述场景中,初始轮廓线与目标边界相距4d,一共要进行8次宽度为d的区域切割,会造成7次对d/2宽重叠区域的重复切割,这种对重叠区域的重复切割对算法并没有贡献。
区域重叠的原因在于初步算法以当前活动轮廓线为中心双向膨胀。而之所以双向膨胀,则是因为算法设定初始活动轮廓线在目标边界附近,即目标边界有可能在初始活动轮廓线内侧,也有可能在外侧,这样在迭代时,部分活动轮廓线要向外侧运动,其余部分活动轮廓线要向内侧运动。因此,可将初始活动轮廓线设定在目标边界外侧,使其仅向内侧单方向运动,即可避免前后邻域重叠,杜绝重复切割,提高算法效率。
(3)单侧变宽域到s-t网络的映射。
由于单侧变宽域是以当前活动轮廓线为基准单侧向内,同时注意到最大流-最小割算法切割所得轮廓线可能经过源点但不会经过汇点,因此将单侧变宽域的内侧边界映射为s-t网络的源点s,外侧边界映射为s-t网络的汇点t。
每个像素点映射为1个网络节点,相邻节点间以8邻域方式连接,边权值为式(2)中的wij。
特别地,s-t网络中的非边界节点与源点s(汇点t)连接的权值为该节点对应像素与单侧变宽域外(内)侧边界中所有8邻域方式相连接的像素的权值累加和。
5.2 设计手自结合纠错
文献[25]给出了一种基于图割的目标提取实时纠错方法,其基本流程如图4a所示:前期方法得到1条局部存在错误的轮廓线,通过鼠标在错误所在区域创建1块“纠错域”(如图4b所示),并对其构造s-t网络(如图4c所示),进行最小代价切割,得到纠错域内正确的目标曲线段(如图4d所示),且该曲线段能够与已有正确的曲线段无缝连接(如图4e所示)。

Figure 4 Later correction of local errors图4 局部错误的后期纠正

Figure 5 Effectiveness verification of preliminary extraction and later error correction图5 前期目标提取与后期错误纠错的有效性验证实验
上述方法能够以交互方式自动实现目标边界错误部分重新提取、正确部分保持不变的纠错功能。但是,自动纠错方式在目标边界不够清晰等较为极端情况下可能会失效,为此,本文对上述方法进一步进行研究分析,实现全手工方式的纠错。
如图4c所示,把s-t网络中所有与汇点t(即纠错域外边界)相连接的边记作:
ET={(k,t)|(k,t)∈E}
(4)
事实上,在调整区中,穿过边集ET的曲线段正是通过鼠标输入的折线线段。若能够控制调整区中的切割线恰好穿过边集ET,即可实现完全手工的纠错方式。因此,
对边集ET,令:
wij=0,(i,j)∈ET
(5)
在调整区中,经过边集ET的切割代价为0,而切割时轮廓线必然经过边集ET,也就是鼠标输入的折线线段,因此可通过设置边集ET的权值为0来实现完全手工的纠错目标。
6 实验分析
本文所用实验平台:(1)计算机:联想ThinkPad X280,CPU Intel i7-855U 1.8 GHz,内存16 GB;(2)操作系统:Windows 7 64位简体中文旗舰版;(3)仿真软件:Matlab R2019a;(4)图像来源:伯克利图像分割测试图库BSDS500(Berkeley Segmentation Data Set and Benchmarks 500)。
6.1 有效性实验
取1幅编号为227092的图像进行目标前期提取及后期局部纠错的全过程有效性验证实验。环状域宽度取20个像素,在目标外围人工勾划1条封闭折线(如图5a所示),以该多边形作为初始活动轮廓线,得到图5b所示提取结果。可见,活动轮廓线错误停止于陶器双耳内侧边界。分别通过2次人机交互干预,错误得到自动纠正(如图5c和图5d所示)。又因陶器底部右侧部分釉面脱落,底座与地面融为一体,致使活动轮廓错误停止于釉面断层处,未能正确停止于底座,当采用自动修正方式时,也因边界不清晰而失败。此时通过完全手工控制鼠标绘制轨迹,将该错误纠正(如图5e和图5f所示)。经过人机交互式的前期提取与后期纠错,得到最终的提取目标(如图5g所示)。
6.2 对比实验
考虑本文算法是图割中基于边缘信息类的提取算法,算法技术路线也来自于经典的GCBAC算法,因而将本文算法与GCBAC算法进行对比。
为保证算法对比科学有效,作以下处理:(1)GCBAC算法无法对彩色图像进行目标提取,因而需先将图像由彩色图像变换为灰度图像,之后根据灰度图像的提取结果获取对应的彩色图像提取结果。(2)约定2个算法的初始轮廓线相同,由于本文算法的活动轮廓线为单侧向内运动,因而初始轮廓线需在目标边界外侧而不是附近。(3)为使2个算法迭代次数相当,方便对比,本文算法邻域宽度取GCBAC算法邻域宽度的一半。

Figure 6 Comparison of extraction result and time consumption图6 提取结果与时间消耗对比实验
实验设定:待提取图像编号124084,像素大小481×321。初始轮廓线相同,GCBAC算法邻域宽度36个像素,本文算法邻域宽度18个像素。
实验结果:2个算法均迭代20次,耗时分别为0.335 s和0.947 s,目标提取正确率分别为95.83%和97.02%。
对比分析:如图6所示,(1)经过前3次(占比15%)的迭代切割,2个算法的活动轮廓线大部分已到达目标边界,剩下的17次(占比85%)迭代切割均用来获取剩余的小部分目标边界段。此时,GCBAC算法邻域定宽不变,对已达段反复切割;而本文算法邻域可变,在已达段邻域宽度为0,切割代价为0,而仅切割未达段所在邻域,切割效率显著提升。(2)随着迭代切割推进,活动轮廓线因贴近目标边界而变长。此时,GCBAC算法因邻域定宽不变,待切割的邻域随活动轮廓线长度增加而增加;而本文算法邻域可变,待切割的邻域随未达目标边界段的减少而减少,从而切割时间消耗呈现一增一减的强烈反差。(3)2个算法目标提取正确率相当,无显著差异。(4)本文算法耗时约为GCBAC算法的1/3。
如表1所示,从测试图库中选取更多图像进行对比实验。本文算法与GCBAC算法平均正确率之比为92.75∶92.78,约为1∶1,平均耗时之比为0.39∶0.99,约为2∶5,结果进一步表明总体上2个算法目标提取正确率相当,无显著差异,但本文算法耗时显著小于GCBAC算法耗时。

Table 1 Comparison of a set of experimental results表1 1组实验结果对比
上述实验结果表明,本文算法既能有效继承经典GCBAC算法目标提取精度高的优点,又能稳定实现算法效率的显著提升。当前期提取结果出现局部错误时,本文算法能够通过简单便捷的人工交互,根据需要手自结合,有效地对局部错误进行彻底纠正。此外,本文算法利用RGB颜色值表征像素距离,实现了彩色图像的目标提取,拓展了算法的应用范围。
7 结束语
目标提取是模式识别与图像分析首要解决的关键问题,也是图像处理的基础课题。因此,设计一个以人为本、快速有效的目标提取算法将为后续的目标特征提取、识别与分类、跟踪与理解等研究打下坚实基础。本文利用图像边缘信息,运用图割理论,提出了一种操作便利、响应快速、提取准确的人机交互式目标提取算法,并在算法后期辅以手自结合的完备纠错机制,满足在医学目标获取与测量等交互环境下的目标提取需求。但是,本文算法在目标背景较为复杂时容易陷入局部极值,造成提取正确率下降。对图像进行降噪预处理、探索新的目标边界特征、融合目标形状先验知识,是进一步提高本文算法提取性能的努力方向。

