基于格式保留的敏感信息加密方案*

张玉磊，骆广萍，张永洁，张雪微，刘祥震，王彩芬

(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070;2.甘肃卫生职业学院,甘肃 兰州 730000; 3.深圳技术大学,广东 深圳 518000)

1 引言

随着大数据技术的成熟，大量敏感信息的安全问题引起了各方关注，如密码、地址、手机号等在未授权下不得公开的信息都属于敏感信息。研究者提出了一系列的加密方案确保安全传输网络信息。现有的数据信息加密方案大多在加密后会对数据进行扩展，使得数据长度和数据类型发生改变[1]。对敏感信息进行加密，需要保证加密后不仅维持敏感数据的基本格式，还应确保不破坏数据用户定义的完整性约束，主要包含数据类型不能改变、不能被扩充等。格式保留加密FPE(Format-Preserving Encryption)能够保持明文的原有格式，把某种格式的明文加密成具有同样格式的密文。

格式保留加密问题在1981年由美国标准局[2]首次提出，2009年，Bellare等[3]将格式保留加密与数据库中的敏感信息保护相关联，提出了基于FPE保护个人信息的方案。2010年，Bellare等[4]提出了基于Feistel网络[5]的格式保留FFX(Feistel-based Format-Preserving)模型。该模型在Feistel网络类型和轮运算方面对Feistel有限集加密模型进行了扩展，可以解决长度为n的字符串构成的消息空间上的FPE问题。2009年，Morris等[6]改进了FFX模型，说明了调整因子的使用方法，设计了一种基于分组密码的模型，通过分组链接CBC(Cipher-Block Chaining)模式可以对字符串进行加密并保持其原有格式。2012年，刘哲理等[7]在已有的格式保留加密模型研究的基础上，提出了先编码后加密的新模型。2012年，李经纬等[8]设计了基于k-分割的Feistel网络保留格式加密方案，支持对任意数据进行FPE加密。同年，李敏等[9]设计了2种可变长度编码字符数据的FPE方案。2016年，Bellare等[10]提出基于Feistel的格式保留加密的消息恢复攻击。2017年，王鹏[11]提出了通过FPE对多类型数据进行加密。2018年，张百惠[12]提出面向大数据发布的保留格式加密技术研究。

在传统格式保留加密方案中，密钥K存储在不同设备中，每个设备直接在K下加密。但是,设备因物理因素处于边信道攻击的风险中。本文基于Bellare等[13]提出的格式保留加密方案，提出了基于身份的敏感信息格式保留加密IBSIFPE(Identity-Based Sensitive Information Format-Preserving Encryption)方案。该方案能够对数据存储、网络传输等应用环境中的敏感信息进行加密保护，同时减少公钥证书的存储和合法性验证，提高信息传输安全性，减少密钥管理系统所需的设施。

本文提出的IBSIFPE方案具有以下几个特点：

(1)与已有的FPE方案相比，本文IBSIFPE方案在混合加密体制下进行，简化了密钥管理，避免了通信前传输密钥的安全风险。

(2)引入身份加密，因此不需要颁发证书。通过密钥派生函数KDF(Key Derivation Functions)生成加密密钥和解密密钥，即使敌手截获了密文和公钥也无法破解。

(3)本方案的安全目标是伪随机置换式安全PRP(Pseudo Random Permutation)，在密钥生成过程中加入身份ID，可以唯一识别其身份信息。

2 IBSIFPE方案定义

(1)系统建立(Setup)：使用安全参数λ，获得系统参数。

(2)公钥派生(PKDF)：通过密钥派生函数输入公钥Ppub身份ID，生成公钥QID。

(3)密钥生成SKG(Symmetric Key Generation)：计算生成用户密钥dID。

(4)加密密钥派生(EKDF)：使用密钥派生函数得到加密密钥K。

(5)IBSIFPE加密(Enc)：发送方使用加密密钥对信息加密，并输出密文c。

(6)解密密钥派生(DKDF)：使用密钥派生函数得到解密密钥K。

(7)IBSIFPE解密(Dec)：接收方使用解密密钥对密文解密，并输出明文m。

3 安全模型

格式保留加密标准的安全目标是伪随机置换安全[14],即要求攻击者无法区分是保留格式加密方案，还是某个随机置换。IBSIFPE方案同样需要满足PRP安全，即要求即使敌手可以截获密文和公钥，也无法破解加密信息。并且，密钥与身份ID相关联，即使解密密钥丢失，造成的损害仅保持在该身份下，不会影响其他身份的通信安全性。

定义1假设A是基于身份的伪随机置换式安全IB-PRP(Identity-Based Pseudo Random Permutation)敌手，C是挑战者，(F,KDF)是1个IBSIFPE方案，若敌手A以不可忽略的优势在游戏中获胜，则称该方案满足适应性伪随机置换安全性。

初始阶段：输入安全参数λ，随机挑选b个比特，把生成的系统参数传送给A，保留系统主密钥s。

阶段1：A适应性地执行下列询问。

加密预言询问：A输入消息m，C使用相应算法，得到密文c。

解密预言询问：A输入密文c，C使用相应算法，得到消息m。

身份查询：A询问身份ID，C运行算法，并将对应用户密钥传送给A。

挑战：A生成2个明文消息m0和m1，以及要挑战的接收者的身份IDr。C随机选择b∈{0,1}，得到密文c并传送给A。

阶段2：A继续执行多项式询问。约束条件是：(1)不能询问目标用户ID的密钥；(2)A无法对密文c执行解密询问。

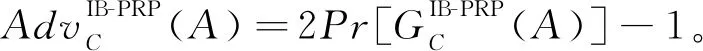
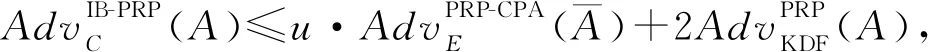
定义3假设存在1个适应性选择挑战ID和选择明文攻击下的语义不可区分安全IND-ID-CPA(IDentity-based INDistinguishable under Chosen-Plaintext Attack)敌手A以ε(k)的优势攻破本方案，A最多进行q1>0次身份询问，对加密预言机至多进行q2>0次询问。那么一定存在1个算法B至少以Advg,B(k)≥(2ε(k))/(e(1+q1)·q2)的优势解决g生成群中的双线性Diffie-Hellman问题。

4 具体方案

(2)公钥派生算法(PKDF)：定义PKDF用于生成用户公钥QID。发送方输入公钥Ppub和身份IDs生成Qs=KDF(Ppub,IDs)，作为发送方的公钥。

(3)用户密钥生成算法(SKG)：输入ID和系统参数，计算身份ID的私钥dID=sQID。

(5)IBSIFPE加密算法(Enc)：给定m和身份IDs，计算QIDs=KDF(Ppub,IDs)，通过加密密钥派生算法计算的K对m执行加密，得到密文c=(C1,C2)，其中C1=U，C2=Enc(K,T,m)。

(6)解密密钥派生算法(DKDF)：接收方输入身份IDr和系统参数，使用密钥派生函数得到解密密钥K=KDF(Ppub,e(dIDr+QIDr,C1))。

(7)IBSIFPE解密算法(Dec)：接收方利用解密密钥对密文c=(C1,C2)解密，获得消息m=Dec(K,T,C2)。

5 方案安全性及性能分析

5.1 正确性及安全性分析

正确性接收方对于得到的密文可以正确解密，根据格式保留加密的要求，加密前后消息格式不变，即发送方和接收方计算的密钥K一致。

□

证明敌手APRP首先挑选1个比特b∈{0,1}。在自适应敌手A切换挑战位前，APRP总是使用它的加密、解密预言来回复A的加密、解密查询。在A进入挑战阶段后，如果b=1，那么APRP继续使用它的加密、解密预言来回复A的加密、解密查询。如果b=0，那么APRP给出的答案从先前的查询答案中随机选择。当A输出其猜测b′时，若b′=b则输出1，否则输出0。我们要求：

□

□

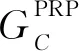
定理4假设基于身份的适应性选择明文攻击的敌手A，以ε(k)优势成功攻击本方案，假设敌手A最多进行q>0次密钥提取询问。那么存在1个不可区分的选择明文攻击IND-CPA(Indistinguishability under Chosen-Plaintext Attack)敌手B，以至少ε(k)/[e(1+q)]的概率成功击破非基于身份的公钥加密方案，运行时间是O(time(A))。那么就有算法B′，以2ε(k)/q的优势和O(time(A))的运行时间解决g生成群中的双线性Diffie-Hellman BDH(Bilinear Diffie-Hellman)问题。

证明由A定义得|Pr[c=c′]-1/2|≥ε，整个过程中算法B′不间断的概率为δq(1-δ)，当δ=1-1/(1+q)时最大，即最大值为ε(k)/[e(1+q)]。存在IND-CPA敌手B以至少ε1=ε(k)/[e(1+q)]的概率成功攻击非基于身份的公钥加密方案，Pr[c=c′|B]=1/2，则Pr[c=c′]=Pr[c=c′|B]·Pr[B]+Pr[c=c′|A]·Pr[A]≤Pr[c=c′|B]·Pr[B]+Pr[A]=1/2Pr[B]+Pr[A]=1/2+1/2Pr[A]，得ε≤|Pr[c=c′]-1/2|≤1/2Pr[A]，即Pr[A]≥2ε。B以至少2ε1/q=2ε(k)/[e(1+q)·q]的优势解决g生成群中的BDH问题。

□

5.2 性能分析

公开文献显示目前没有基于身份的格式保留加密方案，因此无法与同类方案进行效率比较。从表1可以看出，文献[12]中方案是基于对称加密的FPE方案，通过密钥分发中心KDC(Key Distribution Center)产生密钥后，在传输密钥后进行通信。文献[13]在对称加密的基础上引入身份ID，但仍使用该机制。本文方案与这2篇文献中的方案相比，实现了公钥密码体制与格式保留加密的结合，避免了通信前传输密钥的风险，通过派生函数生成加解密密钥，并且保证了PRP安全。

Table 1 Performance comparison 表1 性能对比

6 结束语

格式保留加密不仅可以保证敏感数据的机密性，而且加密前后数据长度和数据格式不变，降低了改造数据格式的成本。本文设计了1个混合加密环境下基于身份的格式保留的敏感信息加密方案。该方案结合了基于身份的公钥加密和格式保留加密的优势，能够对敏感信息进行加密传输，并确保加密前后格式不变。同时，提高了通信安全性，减少了密钥系统的相关设施。本文方案保证了基于身份的PRP安全并满足IND-ID-CPA安全。