基于非负矩阵分解法的抗水分干扰土壤有机质高光谱估算
丁仕杰,宋海燕,张智峰,韩小平
(山西农业大学 工学院,山西 太谷 030801)
土壤有机质(Soil organic matter, SOM)是植物和微生物生长所必要的营养物质[1,2]。有机质含量高的土壤既能为作物提供丰富的养分,还能减少土壤养分的流失。实时检测土壤有机质含量,对保持耕地土壤有机质平衡,提升农作物产量等有很大帮助。高光谱技术有快速、高效、低成本等优点,普遍应用于土壤有机质定量检测。近红外波段中土壤水分(Soil moisture,SM)对土壤有机质的检测有一定的干扰[3],是影响测量准确性的一个主要原因。
近年来,国内外学者尝试用各种方法来消除水分对土壤有机质预测的影响,以实现其预测精度的提高。Minasny等[4]将Roger等[5]提出的外部参数正交化(External parameters orthogonal neural network,EPO)运用到去除土壤水分对有机质检测的影响中;Changkun Wang等[6]基于EPO提出了一种新的EPO策略(EPOII),运用这种预处理方法提高了湿土土壤有机质的预测精度;陈奕云等[7]应用直接标准化(Direct standardization,DS)对湿土光谱进行校正,降低了湿度差异对光谱反演土壤有机质的影响;Ji W等[8]用分段直接标准化(Piecewise direct standardization,PDS)对近红外区域有机碳的估计进行了改进,提高了有机质的估测精度;An等[9]设计了水分吸收指数MAI,参考土壤水分梯度提出了相应的修正系数并建立土壤全氮预测模型,所测数据精度较原始模型有明显提高。然而上述方法均没有得以推广,由此可见,消除水分影响,提高土壤有机质预测精度仍是一迫切需要解决的问题。
本研究在分析比较了干土和其对应不同含水率下湿土吸光度谱图特性曲线的基础上,利用非负矩阵分解法可以从原始矩阵中提取出基础和特征2个不同的非负矩阵、完成对特征数据分离提取的特性,提出采用该方法实现削弱近红外波段中水分对土壤有机质含量预测影响的目的。
1 材料和方法
1.1 试验材料
1.1.1 研究区域概况
本文以山西省晋中市太谷县为研究区域。该区域位于山西省晋中盆地东北部,区域位置为112°28'~ 113°01′E,37°12′~37°3′2 N。其地貌形态有山地、丘陵、平原3种。该区域土壤类型为褐土,是该省主要地带性的土壤,同时也是我国北方主要的农业土壤。
1.1.2 土壤样本的制备
在太谷县内不同地区采集了50个土壤样本,采集过程及不同含水率土样的配置方法如下:
(1)土样采集:采集地面以下5~15 cm的土壤并除去土壤表面杂质。
(2)风干:将采集的土壤样本平铺置于实验室通风处,连续风干3 d。
(3)过筛:将风干后的土壤样本碾碎过2.5 mm筛子,去除大颗粒土壤。
(4)烘干:将土样各自均匀地放置于托盘上,用烘干箱在106 ℃下烘干至恒重,取出后分类放置在密闭的塑封袋中。
(5)配制不同含水率的土样:取同一土样,称取相同重量的4份,分别放入干净的烧杯中,加水配制5%、10%、15%、17%的样本。用保鲜膜将烧杯密封后静置3 d,静止期间可通过摇晃烧杯使水分均匀扩散到土壤中。土壤质量含水率计算见公式(1):
(1)
式中,M0为湿土质量/g,M1为干土质量/g。
1.2 试验方法
1.2.1 土壤有机质标准值测定
用重铬酸钾容量法测定土壤有机质的标准值。在外加热的情况下,用一定量的标准重铬酸钾-硫酸溶液氧化土壤样本中的有机碳,之后用标准的硫酸亚铁溶液滴定多余的重铬酸钾,直到溶液颜色变红且不再变化。所测土样有机质含量的计算见公式(2):

(2)
式中,c为硫酸亚铁标准溶液的摩尔浓度/(mol·L-1),V0为空白实验中使用硫酸亚铁标准滴定溶液的体积/mL,V为测定时硫酸亚铁标准溶液消耗的体积/mL,0.003为1/4碳原子的摩尔质量/(kg·mol-1),1.724为有机碳换算为有机质的系数,m为称取的试样质量/g,D为稀释倍数。
1.2.2 光谱数据采集和预处理
本试验采用ASD公司生产的FieldSpec3高光谱仪,采集波长范围为350~2 500 nm。350~1 000 nm范围内采样间隔为1.4 nm,1 000~2 500 nm范围内采样间隔为2 nm。测量时将土样置于培养皿中并用尺子将表面刮平,放入暗室内进行光谱数据采集,采集时每个样本旋转 120°测量3次,每次扫描3条,即每个样本共获得9条光谱数据,单条扫描时间为0.1 s。
为获得光滑且连续的光谱,原始高光谱数据用仪器自带的View SpecPro软件进行预处理,包括求均值(Mean)、拼接校正(Splice Correction),再经过ASCII Export导出数据并整理到Excel表格。
1.3 数据处理及分析方法
1.3.1 非负矩阵分解法
非负矩阵分解(NMF)属无监督学习方式,是一种在概率矩阵分解的基础上对分解完成的矩阵加以非负限制的计算方法。它将一个非负矩阵V分解为2个非负矩阵W和H,具有可提取部分特征来感知整体的能力。并且NMF的算法与线性光谱混合模型(Linear Spectral Mixing Model,LSMM)十分契合[10],因此可以把NMF这一方法应用到高光谱数据的波谱混合分离中。本文采用的是林智仁等[11]提出的基于投影梯度的NMF算法,相关数据计算基于Matlab2014b软件编程实现。实现方法见公式(3):
Vn×m≈Wn×k×Hk×m
(3)
同时要求:Wn×k≥0;Hk×m≥0。
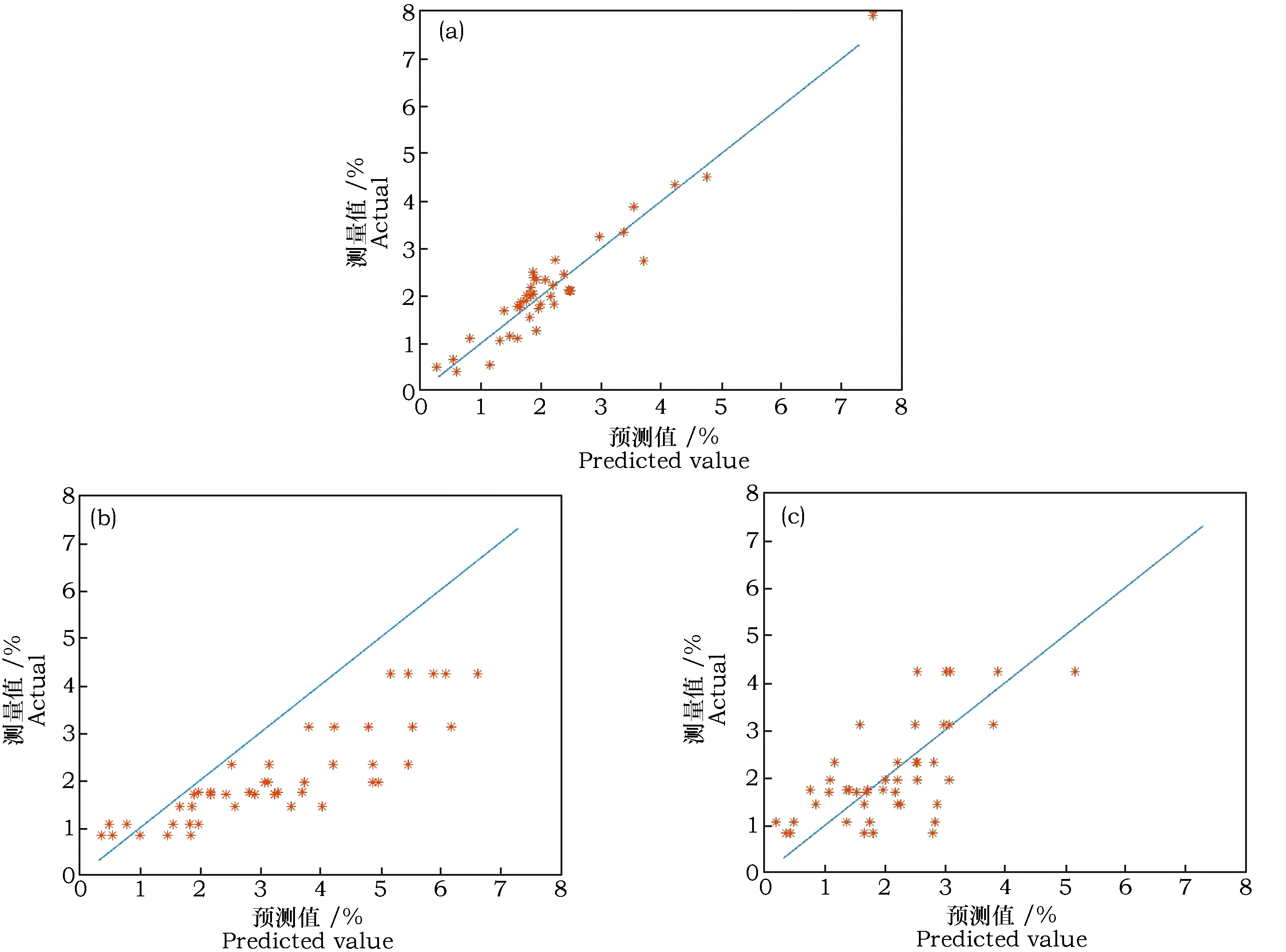
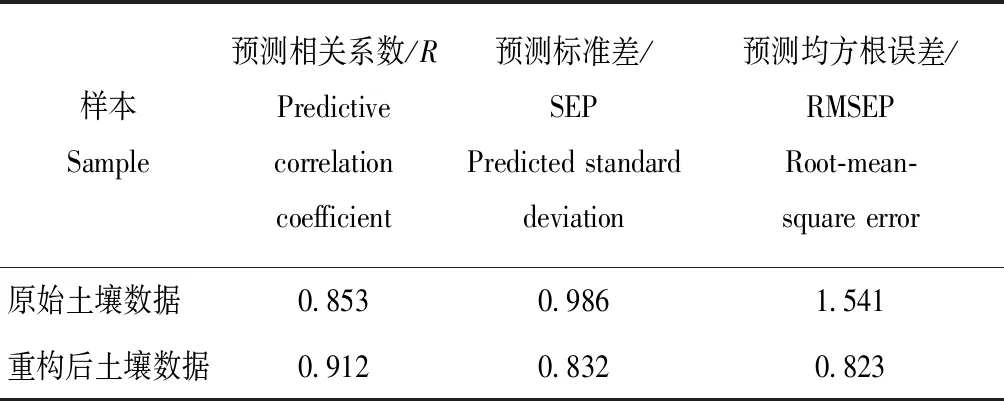
式中:Vn×m为原始矩阵;Wn×k为基础矩阵;Hk×m为特征矩阵。一般情况下要求k远小于m,即满足(n+m)×k NMF是一种困难的非确定性多项式(Non-deterministic Polynomial,NP)求解问题,可以将其看作是一个优化问题,用迭代法求解。式(3)的乘法更新迭代法则见公式(4)和(5): (4) (5) 经典的NMF算法收敛速度比较缓慢,可通过使用投影梯度法加快收敛速率,这种方法虽然过程比较复杂,但整体收敛效率更快。由于分解后的矩阵中无负数元素,故原矩阵Vn×m中的列向量可以看作分解后Wn×k矩阵列向量的加权和,基础系数为Hk×m矩阵中对应列向量的元素(称为系数矩阵)[15]。 1.3.2 偏最小二乘 偏最小二乘(PLS)是一种集成了主成分分析、典型相关性分析、线性回归分析优点的多元统计分析技术,可以在提取出数据中主要特征的同时去除数据中的噪声和自变量之间的多重相关性[16~18]。 PLS所建模型的质量通常采用以下几个统计参数来评定: (1)相关系数R,该参数用来描述自变量与因变量之间的线性相关度,求解计算见公式(6): (6) (2)预测标准差SEP,该参数用来评判预测数据偏离算数平均值的程度。求解计算见公式(7)和(8): (7) (8) 式中:Ip为预测集样本数;y^i为预测集样本的预测值;yi为预测集样本的实测值。 (3)预测均方根误差RMSEP,该参数是预测集样品的预测值和实际值之间误差大小的数学反映。求解计算见公式(9): (9) 用重铬酸钾容量法对50个土样的有机质含量进行测量,统计结果如表1所示,各样本有机质含量分布无规律,有较大的标准差与变异系数,大多数样本有机质含量分布在均值±2倍标准差以内,适合反演模型的建立,具有很好的代表性。 表1 土样有机质含量统计参数Table 1 Statistical parameters of soil sample organic matter content 土壤由多种成分组成,其组成成分和内在性质对其光谱特性有很大的影响。图1为有机质含量为1.116%的土壤在不同含水率下的光谱图,图中横坐标为波长(nm)、纵坐标为吸光度值(lg(1/R))。 图1 有机质含量为1.116%的不同含水率土壤的光谱图Fig.1 Spectra of a soil sample with 1.116% SOM under different moisture content 从图1可知,有机质含量相同的土壤在不同含水率下的谱图曲线变化趋势相似,整个区域内吸光度值随土壤水分含量的升高而增大,且在1 410 nm和1 920 nm波段附近有较强的吸收峰,这两个吸收峰是由水分子中的O-H键引起的[19~23],吸收峰的宽度和高度随含水率的增大呈上升趋势。表明土壤水分对土壤有机质近红外光谱的检测有很强的干扰。 把经预处理后的50个土样在5种含水率(干土、5%、10%、15%、17%)下的共250组高光谱数据看作是2 121个波段,250个样本所组成的矩阵Vn×m(m为光谱波段,n为样本数),用NMF法将原始矩阵分解为基础矩阵Wn×k和特征矩阵Hk×m。然后将分解后的干土的Wn×k矩阵(相对纯净且不受土壤水分和测定条件的影响[24])与湿土的Hk×m矩阵根据公式(3)进行融合得到新的光谱数据Vn×m。图2是以有机质含量1.116%为例得到的不同含水率土壤及其重构后的吸光度谱图。 由图2可知,各含水率土样数据经NMF分解重构后,在可见光范围内,含水率为15%和17%的土样重构后的吸光度值较干土有明显减少,在近红外波段范围内,除1 920 nm处的吸收峰略高于原始干土样本外,各含水率土样重构后的谱图曲线与干土谱图曲线重合效果非常好,说明在近红外区域,该方法可以很好地削弱水分影响,重现原始干土光谱特性。 图2 不同含水率土壤及其重构后的光谱数据Fig.2 The spectra of soil with different water content and its reconfiguration 此外,在运用NMF方法对土壤光谱数据进行波谱分离时,发现分离出的特征矩阵噪声含量较多,故尝试对不同含水率土样分离后的特征矩阵进行平滑度为3、5、10、20和30的平滑去噪处理,之后分别将干土的基础矩阵与经过平滑处理后不同含水率土样的特征矩阵以及未经平滑处理后不同含水率土样的特征矩阵根据公式(1)进行融合,得到2组新的光谱数据,用偏最小二乘法对其进行建模预测以评价各平滑处理的效果。结果表明:当平滑度为10、20和30时,因为平滑间隙过大,丢失了有用信息,预测相关系数均小于未经平滑处理得到的预测相关系数,当平滑度为3和5时,预测相关系数与未经平滑处理得到的预测相关系数非常相近,说明在NMF计算中已经将土壤光谱数据中的噪声分离到基础矩阵中,简化了试验步骤。 鉴于室内光谱可控因素较多,模型鲁棒性好,且NMF重构后可以在近红外区域较好地实现原始干土土样的特性曲线,为此,本研究在750~2 500 nm波段范围内采用PLS法对室内采集的41个干土样本的光谱数据建立土壤有机质定量预测模型,9个土样在5种含水率(干土、5%、10%、15%和17%)下经NMF处理前后的共45个光谱数据作为预测集进行预测分析验证。所建模型对校正集和预测集的预测效果如图3所示,(a)为所建模型校正集的预测效果(校正相关系数为0.962,校正标准误差为0.356,校正均方根误差为0.381),(b)为NMF处理前原始土壤数据作为预测集的预测效果,(c)为经过NMF分解重构后的土壤数据作为预测集的预测效果。 (a)校正集;(b)原始土样预测集;(c)重构土样预测集 (a)Correction set;(b)Original soil prediction set;(c)R-constructed soil prediction set图3 校正集和预测集的预测效果Fig.3 The prediction effect of correction set and prediction set 为了定量分析模型的预测精度,运用公式(4)~公式(7)分别计算出预测相关系数R、预测标准差SEP和预测均方根误差RMSEP,模型统计参数表如表2所示。 表2 土壤有机质含量预测模型的统计参数 由表2可见,经过NMF方法重构后预测相关系数较原始土样提高了0.059,预测标准差(SEP)降低了0.154,预测均方根误差(RMSEP)降低了0.718。预测相关系数R越大,预测标准差SEP和预测均方根误差RMSEP越小,模型预测效果越好[25,26],表明NMF分解重构后可以削弱水分对土壤有机质检测的影响。 近红外光谱能够通过对有机物特征官能团的特征吸收检测,确定未知物的化学结构以及含量,土壤有机质高光谱检测便是基于这一原理。湿土土壤中水分子的O-H键在近红外波段中有很强的吸收作用,影响了有机质含量的检测[27]。曾静等[28]在近红外光谱中检测紫色土有机质含量时发现,土壤水分在近红外波段有较高的吸收系数,直接影响了近红外技术检测有机质含量的精度。于雷等[29]研究发现水分中O-H键对近红外光谱有明显的吸收,影响了近红外波段土壤有机质含量的估测。以上研究结果均与本研究结果一致,说明水分对土壤有机质的光谱特性造成了影响。 本研究运用NMF法对土壤数据进行分解重构,得到新的光谱特性曲线,且重构后的光谱特性曲线与原干土的光谱特性曲线重合效果好,与陈红艳等[24]的研究结果一致。用偏最小二乘对室内光谱数据建立有机质含量预测模型,分别对重构前后土样预测的有机质含量进行对比分析,用预测相关系数R、预测标准差SEP和预测均方根误差RMSEP作为统计参数对模型质量进行评定[30,31]。结果表明NMF能够在很大程度上削弱水分对土壤有机质近红外光谱检测的影响,提升了对湿土土壤中有机质含量的预测精度。 本研究针对在土壤有机质高光谱检测中,影响其检测精度的主要因素水分开展研究工作,在研究过程中发现光谱反射率受含水率影响的同时,土壤粒径也对其有一定影响[32],后续的研究将综合考虑这两因素,通过与参数校正等方法的结合进一步提高预测精度。
2 结果与分析
2.1 土壤有机质含量

2.2 不同含水率土壤光谱特性

2.3 基于非负矩阵分解的土壤水分影响消除

2.4 偏最小二乘建模预测
3 讨论与结论

