基于最小角度回归模型的NIR光谱果品品质分析方法

但松健

(重庆第二师范学院 继续教育学院，重庆 400067)

果品的内在品质(如可溶性固形物、可滴定酸含量以及维生素C等)是决定其市场价值的重要因素之一，然而当前市场上以次充好等情况时有发生，如何对果品的内在品质进行精确快速检测正逐渐成为当前亟待解决的问题。传统的果品质量检测手段主要通过随机抽样的方式进行破坏性的检测，样本的制作及检测流程较为复杂，因此耗时费力，检测成本高[1～3]。近红外(Near infrared，NIR)光谱具有无损、高效、精确以及低成本等特点，得到了越来越多研究者的重视[2, 4～10]。但在基于NIR光谱的果品品质检测中，一方面采集的光谱数据存在着数据维度较高，通常难以与果品品质建立直接关联，另一方面，光谱数据收集过程中还存在着许多不可避免的各种噪声，这对于光谱数据和质量参数之间关系模型的建立造成了一定的影响，同时也给果品品质检测造成了干扰。针对上述高维度、存在噪声的NIR光谱数据，如何基于机器学习算法建立与果品品质的质量回归分析模型，是能否实现果品品质定量分析的关键。

本文主要就基于回归模型的NIR光谱果品品质检测进行详细探讨，首先分析线性和非线性2种现有的果品品质检测方法，其次提出一种基于最小角度回归的果品内在品质检测算法，并与传统的线性回归方法(最小二乘法)和非线性回归方法(最小二乘支持向量机)在预测准确率、计算复杂度和模型可理解性方面进行对比，以探讨本文所述算法在NIR光谱果品品质分析中的优势。

1 传统NIR光谱果品品质回归模型

1.1 线性回归模型

基于线性回归模型的机器学习算法是进行NIR光谱分析并以此来决定果品质量的重要方法之一。其中偏最小二乘回归(Partial Least Squares Regression, PLSR)是最常用的果品质量分析方法[1, 2, 5～7, 11～13]。PLSR是一种多元统计分析方法，主要研究多因变量对多自变量的回归建模，包括主成分、多元线性回归以及相关性分析等多种方法。当各变量内部高度线性相关时，PLSR模型更有效，特别是在NIR光谱数据集中变量个数往往远大于样本个数，但各个变量间存在信息冗余，因此PLSR能很好的建立回归模型[14]。

1.2 非线性回归模型

除了线性回归，非线性回归方法也被大量的用于果品品质检测[4, 9, 15～17]。特别是由于NIR采集过程中存在光散射的影响，因此预测值与NIR光谱之间存在着某些非线性关系，针对这些非线性光谱特征进行处理，采用非线性回归方法往往能获得一定的预测精度[18, 19]。其中，最小二乘支持向量机(Least Squares Support Vector Machines，LS-SVM)是应用最多且效果较好的NIR光谱分析方法。LS-SVM由SVM算法发展而来，由Suykens等人提出[20]，通过使用L2范数进行目标函数优化，并将支持向量机中的不等式约束替换为等式约束条件，使得LS-SVM的优化问题可以通过Kuhn-Tucker条件得到的一组线性方程组求解。

虽然非线性回归模型在处理非线性数据和准确率方面具有一定优势，但在NIR光谱分析模型的可解释性(找到最有代表性的特征)方面，线性回归模型更优。此外，还有其他特定的寻求最优特征的方法[21]，但这些方法由于模型复杂度较高，难以应用到实际中。相比而言，基于线性回归的方法更为简单、直观，且在NIR光谱分析中更容易理解，运用也较广泛。

2 基于最小角度回归(LAR)的果品品质检测

最小角度回归(Least angle regression，LAR)是一种基于线性回归的方法，虽然已在其它领域得到了广泛应用，但利用LAR进行果品质量检测还鲜有报道。因此，本文将LAR方法与其它线性和非线性方法就果品品质检测的预测精度、计算效率和模型可理解性等方面进行对比，为基于机器学习的NIR光谱果品品质检测提供了新的思路和新方法。

2.1 向前逐步回归和逐渐回归

NIR光谱具有特征维度较多的特点，例如在本文中，针对柑橘的品质检测提取了波长范围1 000～2 499 nm，间隔为1 nm的共计1 500维的光谱信息，如果直接进行回归分析，将由于变量数过多导致无法得到关于回归参数的精确解，因此对于维数过多的回归分析，进行变量选择非常重要。最直观的变量选择方法是通过将所有变量的组合排列进行遍历，并逐个进行回归测试，从而选出最优的变量组合。虽然这种方法能得到最优解，但由于其庞大的计算量使得模型难以应用。因此，实际中变量的选择是通过某种算法寻求一个计算量较小且能接近最优变量组合的次优解实现的。其中，向前逐步回归(Forward stepwise regression)和向前逐渐回归(Forward stagewise regression)是目前常用的基于特征选择的回归方法。

向前逐步回归的思路是从回归模型所有系数为0开始，从候选变量中选出一个最能改进模型的回归误差的变量，即通过加入该变量能最大程度减少初始模型在当前的残差平方和，然后对回归系数进行重新评估[22]。之后继续按照上述方法进行迭代选择候选变量，直到达到拟合精度为止。由于每次选择都使用了贪心算法即考虑最能改进模型误差的变量，因此对于所有入选的变量都重新进行了回归分析，也就是每一步都进行了多元回归。

逐渐回归方法与逐步回归的方法类似，但其改进了逐步回归中由于贪心算法带来的负面影响[23]。逐渐回归方法也从零系数的回归模型开始，首先找出与当前残差相关系数最高的变量，并再次进行回归分析，同时逐渐回归模型只针对部分的系数进行更新。在下一次选择中，其仍然针对于当前残差相关系数最高的变量进行选择，并重复上述步骤，直到达到回归精度。在逐渐回归的变量选择过程中，如果某个变量比其他变量更具有早期优势，则这一变量可能会多次选中并进行系数更新。逐渐回归每一步并非充分地求解全部回归系数，因此相比逐步回归，逐渐回归能获得更好的结果。

2.2 最小角度回归(LAR)

LAR方法参考了逐渐回归方法的思想，但使用了更为有效的计算方法。逐渐回归算法每一步仅选择一个变量，并且只更新该变量的系数，从而减少了当前残差和当前被选择变量的相关性，但是经过重复类似的步骤后，以前被选入激活的变量和当前残差的相关性有可能又变成最小而又被再次选入。因此，在逐渐回归每一步中只有该步入选变量的系数进行了修改，而其他已入选变量系数并没有变化，从而导致收敛速度慢。而LAR算法正是对该问题进行修正，其每一步变量选择过程中都会保持当前的残差和所有入选活跃集变量的相关性，即同时修正所有入选变量系数，使得这些变量和当前残差的相关性会同步减少[23]，从而减少了迭代次数。

3 结果及讨论

本文利用基于最小角度回归(LAR)算法的果品品质检测模型，对16个地区的1 600个柑橘样本(每个产地平均收集100个果实)进行了不同品质参数的果品品质检测，并与目前现有的线性和非线性的品质检测模型进行了预测准确度和计算复杂度等方面的比较。

3.1 试验数据集及评价指标

本文的试验数据集均采集自16个地区的不同的柑橘样本，其中光谱波长分布为1 000～2 499 nm。由于光谱采集设备中不可避免存在噪声，所以首先采用Savitzky-Golay卷积平滑法对原始光谱信号进行去噪。其次，为避免测试中样本选择偏差，采用5×10次交叉验证的方法进行试验，即每次选择1 280个(占样本总量的80%)样本进行训练，剩余样本作为测试数据，依次循环5次，并将上述过程重复10次，共进行了50次训练和测试，将最终的平均值作为性能结果输出。在果品质量参数方面，每个果实都对应测定了可溶性固形物含量(TSS)、可滴定酸度(TA)和VC含量等品质参数。

可溶性固形物含量(TSS)反映了柑橘的甜度，因此是一个非常重要的品质指标。在每个地区的样本中随机抽取20个果实，进行榨汁后利用多层纱布进行过滤，将果汁混匀后，取过滤后的上清液作为试样。采用手持数显折射仪(ATAGO，PAL-ES3，Japan)进行测定。

可滴定酸含量(TA)反映了柑橘的酸度，也是一个影响柑橘口感的重要指标。由于柑橘果汁中的酸主要以柠檬酸为主，因此采用中和酚酞指示剂滴定法进行可滴定酸含量测定。首先准确吸取10 mL的柑橘果汁样本，加入不含二氧化碳的蒸馏水稀释至100 mL，摇匀后用移液管取稀释液10～100 mL，加入1%酚酞指示剂2滴，并用氢氧化钠标准溶液进行滴定，至溶液出现均匀桃红色30 s内不褪色为终点，并记下所消耗的体积，最终的含酸量可以由式(1)求得。

TA/%=N×V2×0.064×100/G

(1)

式中，N为氢氧化钠标准溶液摩尔浓度/(mol·mL-1)；V2为滴定时所消耗的氢氧化钠标准溶液的体积/mL；G为用于滴定的果汁体积/(10×10/100)mL。

对于VC含量的测定，不同种类及品种的柑橘由于受不同栽培条件、不同成熟度、不同贮藏条件等影响，导致其果实中的VC含量也有所不同。本文主要采用2,6-二氯吲哚酚钠滴定法。首先精确吸取10 mL的柑橘果汁样本，加入质量浓度为1%草酸溶液稀释至100 mL，之后取稀释液2～50 mL至容器中，使用0.05%的2,6-二氯吲哚酚钠溶液进行滴定，至溶液为均匀浅红色为止，并记录所消耗的2,6-二氯吲哚酚钠溶液测定还原性VC含量，可以由式(2)得到。

VC/(g·100 L-1)=H×V×100/G

(2)

式中，H为2,6-二氯吲哚酚钠的滴定度/(g·L-1)；V为滴定所消耗的二氯吲哚酚钠体积/mL；G为用于滴定的果汁体积/(2×10/100)mL。

回归性能评价指标包括：

(1)校准相关系数(R)：

(3)

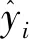
(2)校正均方根误差(RMSEC)：

(4)

RMSEC值越大，表示拟合的误差越大。

(3)预测相关系数(r)：

(5)

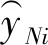
(4)预测均方根误差(RMSEP)：

(6)

RMSEP表示在测试样本集上的预测值与真实值之间的误差均方根，其值越小，表示预测越精确。

(5)偏移(Bias)：

(7)

偏移与RMSEP相似，Bias衡量测试集的预测值与真实值之间的误差平方根，其值越小，同样也表示预测越精确。

3.2 试验结果与分析

(1)预测结果性能分析

为了与本文提出的LAR模型进行对比，首先采用Matlab软件计算了线性模型PLSR以及非线性模型LS-SVM在测试数据集上基于TSS、TA以及VC等品质参数的结果(表1)。

表1 测试模型LAR、PLSR和LS-SVM在TSS、TA和VC上的性能结果

从表1可以看出，LAR回归模型明显优于常用的线性回归方法PLSR，其中在预测质量参数TSS上，LAR在相关性能指标如相关系数r以及预测误差指标RMSEP上得到了0.882 5以及0.679 5的结果，而PLSR方法在预测TSS上的r和RMSEP上仅得了0.857 1以及0.763 1。对于质量参数TA，LAR的预测性能r和RMSEP分别为0.800 5以及0.124 8，而PLSR方法在预测性能r和RMSEP上仅得到了0.783 6和0.127 3。在质量参数VC上，LAR的预测性能r和RMSEP分别为0.816 0和5.208 3 g·100 L-1，PLSR在r和RMSEP分别为0.782 3以及5.614 1 g·100 L-1。因此LAR在各个质量参数上以及性能指标上均优于常用的线性PLSR模型。

当然在表1中，非线性的LS-SVM模型获得了最佳的预测性能，其中在TSS上，LS-SVM获得了最佳的r和RMSEP分别为0.899 0以及0.631 6；在TA上为0.800 8以及0.124 6；在VC评价上为0.817 6和5.180 4。其可能的原因为，NIR光谱中存在的非线性噪声，采用非线性的LS-SVM在处理此类数据时具有一定的优势，从而得到了均优于线性模型LAR和PLSR的预测结果。

虽然PLSR在预测性能最差，但是在训练过程中，其得到了所有性能指标中最佳的拟合精度，其中在TSS、TA和VC上R分别达到了0.933 5，0.950 1和0.951 4。说明PLSR有可能进行了过度拟合的训练，造成了在预测时泛化性能下降。事实上，对于高维数据的拟合，由于样本数往往小于特征维数，如NIR光谱数据集就普遍存在着这样的问题，往往更容易造成线性回归模型训练不足从而造成过拟合，因此对于PLSR模型在基于NIR光谱分析的品质检测中，表现不如LAR以及LS-SVM具有一定的必然性。

LS-SVM在预测性能上优于LAR方法，在处理NIR光谱时，可能由于光散射效果造成的非线性关系[24]的数据分布，虽然这种非线性的干扰效果可能并不明显，但还是造成了线性方法LAR和非线性的LS-SVM之间的性能部分差距。

(2)计算复杂度及计算效率

虽然LS-SVM能获得比线性方法LAR和PLSR更优的性能，但在实际应用中，PLSR方法仍然是许多研究人员更常用的方法，其中一个重要的原因就是LS-SVM在实现以及计算上要复杂得多。特别是在大型的数据集上，PLSR在计算效能方面确实具有一定的优势，而LAR则在处理速度上更加优于PLSR算法。

另外，LS-SVM还需要对对应的核函数参数以及支持向量机惩罚因子C进行适当的选择，否则容易造成性能的下降。而PLSR和LAR模型均只有单一参数即需要选入特征的数量需要确定。更多的参数在实用中意味着更多的不确定性和复杂性，同时为了得到最优的参数，还需要额外的计算工作对参数进行优化选择。因此在实际应用中，线性的方法更为有效的用于果品品质的快速检测。

为了对以上3个模型的计算效能进行对比，本文对基于柑橘NIR光谱的TSS质量参数进行了预测，并统计了和分析了3个模型的所需的预测时间。同时为了对在不同数量的特征情况下的性能进行分析，本文在进行对比时还使用了不同的NIR光谱维数，其中维数从100到1 500以间隔100进行了多次试验。最终本文对来自16个地区的不同的柑橘样本在不同光谱维度上进行了TSS质量分析。其中仍然采用了Savitzky-Golay卷积平滑法对原始的光谱信号进行去噪，以及利用了5×10的交叉检验法取平均性能作为比较输出。

详细的试验流程为：首先，获得各个模型的在每个数据上的最佳参数；其次，利用各个回归方法在TSS质量上进行训练以得到最佳参数下的相关的回归模型；最后，利用得到的模型对测试数据集进行质量分析并获取相应的性能指标。由于计算最优的参数是实际应用中必不可少的步骤，因此本文统计了从获取模型最佳参数开始到对测试数据集进行质量分析的整个过程的时间，作为计算效能的对比依据。其中为了对LS-SVM的最优参数进行获取，本文采用传统的网格搜索算法进行相关参数的选择优化。对于PLSR和LAR方法，采用了交叉验证的方法来确定最优的参数。

其中各个模型的计算复杂度用对TSS进行质量分析的运行时间来衡量(图1)。其中可以清楚的看出，LS-SVM需要耗费比PLSR和LAR明显更多的时间，特别是随着维数的增长，虽然在耗时方面存在一定的波动，但所耗的时间总的趋势是在不断的攀升。LS-SVM在即使只采用部分光谱数据例如300维的光谱信息时，仍然需要近50 s的时间，而在采用1 000维以上的数据进行试验时，其所耗费的时间甚至超过了60 s，时间增加了近10 s之多。

而对比LS-SVM，PLSR和LAR在耗时方面随维数的增长极为缓慢切较为线性，所耗时间也较少，即使采用了1 500维特征进行训练和测试，PLSR也只要10 s以下的时间，而LAR仅需要5 s左右的时间即完成了所有的试验过程。

以上试验结果和分析说明，在计算性能上，LAR具有比PLSR更优的性能，且明显优于LS-SVM。

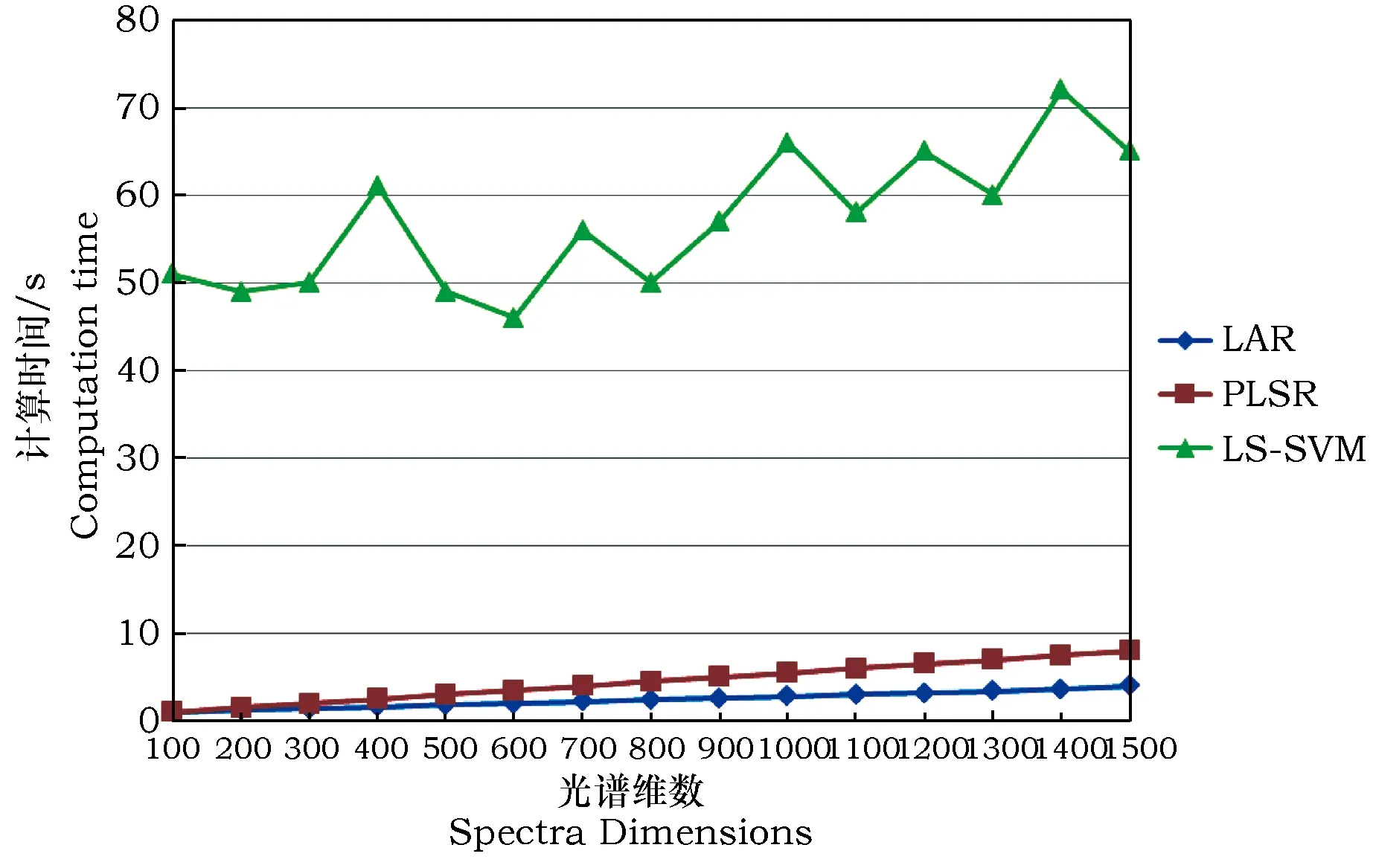
图1 在不同的NIR光谱数据维数上利用LAR、LS-SVM以及PLSR对TSS进行质量分析的时间复杂度Fig.1 Computation time of LAR, LS-SVM and PLSR to predict TSS content based on different dimensions of NIR spectra

(3)模型的可解释性与光谱分析

除了预测准确性以及计算效能以外，在某些实际应用中，模型的可解释性也是预测模型需要关注的方面。例如，在对基于NIR光谱的TSS质量预测中，期望能够明确哪些是最能影响TSS质量的光谱波段。其中光谱的指纹图谱分析(Spectral fingerprint analysis)是常用的找出与感兴趣参数最相关的光谱波段或者数值的方法[25]，也被称为光谱特征的重要性分析(spectral variable importance analysis)。通过预知光谱中最为重要的波段，可以更有针对性和选择性的收集相关的光谱数据。LS-SVM虽然在预测准确率上具有一定的优势，但由于其需要通过非线性核函数将特征映射到高维空间中进行处理，因此这些映射到高维中的特征在相关的光谱波段解释上较为困难，有些甚至是映射到了无限的空间尺度上。而线性回归方法较为直接和简单，因此线性回归方法在光谱指纹分析中更为常用。通过挖掘光谱中波长信息与PLSR的隐含变量以及回归系数之间的关系，可以得到信息量最大的光谱信息，而PLSR回归系数同样也隐含着对应光谱信息的重要性。也就是说，相关波长所对应的回归系数越大，则比回归系数较小的波长更为重要。由于PLSR模型使用了多个隐含的回归变量，因此在使用回归系数对波长信息进行分析时更为方便。LAR同样也是线性回归模型，其具有与PLSR模型相同的可解释性以及光谱指纹分析能力。

PLSR和LAR基于 NIR光谱进行TSS质量分析时的可解释性(模型的回归系数在不同NIR光谱的波长信息上的分布情况)分别如图2(a)和图2(b)所示。

(a)PLSR回归系数；(b)：LAR回归系数(a)PLSR regression coefficient; (b) LAR regression coefficient图2 LAR和PLSR模型的回归系数值在不同的NIR光谱波长信息上的分布Fig.2 LAR and PLSR regression coefficients on different wavelengths of NIR spectra

从图2可以看出，PLSR和LAR模型在系数上具有相似的脉冲分布模式，例如在波长为1 082 nm和1 083 nm处，LAR和PLSR模型都有同样的系数峰值。类似的，在1 317～1 320 nm(C-H组合的第1个谐波)、1 608～1 612 nm、1 686～1 688 nm、1 872～1 875 nm(C=O 键的第2个谐波)、2 030～2 038 nm处，PLSR和LAR模型都出现了相似的系数峰值分布；但相比PLSR，LAR模型系数分布峰值更加明显和直观，也就是说，LAR模型的回归系数更集中分布在少量的非零系数的波长上。而PLSR的系数值则较为均匀地分布在所有的波长上，分布较为扁平。其原因是NIR光谱中在不同波长中存在着很高的共线性，某个特定波长的回归系数可能受到其他共线波长的影响。这种共线性也使得PLSR模型在某些特殊波长上的系数分散，从而在分布上不能形成明显的峰值。例如，对于LAR模型在1 393～1 394 nm处(CH3谐波)有一个明显的峰值，但在对应的波长上PLSR模型却没有形成明显的系数值波峰，即这些较大的回归系数值被许多相关联的波长信息所共享。

综上，本文对提出的LAR模型与常用的线性模型PLSR以及非线性的LS-SVM算法在果品TSS、TA和VC检测上进行了对比，其中LS-SVM能获得较好的预测性能，但在计算效能和可解释性方面弱于线性LAR和PLSR模型；同时LAR在预测性能上明显优于PLSR模型，且比PLSR模型更有利于NIR光谱指纹的分析。因此，本文提出的LAR模型为基于NIR光谱的果品质量分析提供了较好的解决方案。

4 结论

本文研究了利用最小角度回归(LAR)模型对基于NIR光谱的果品内在质量进行分析的方法。

(1)在分析目前线性和非线性果品品质检测方法的基础上，提出了基于LAR模型的果品内部品质分析方法。LAR模型是一种基于变量选择的方法，能获得比向前逐步回归更优的回归效果。

(2)试验数据集中，波长集中分布在1 000～2 499 nm，同时提取的果品质量指标包括TSS，TA和VC。在预测准确度上，LS-SVM模型达到了最优预测性能，而LAR模型明显优于目前最常用的线性PLSR模型。在计算复杂度上，LAR和PLSR模型明显优于LS-SVM模型。在模型的可解释方面，LS-SVM不能用于光谱指纹分析，而LAR要优于PLSR模型。

(3)虽然LAR模型在预测精度上稍逊于LS-SVM，但在模型的实现和计算复杂度以及可解释性方面都具有明显的优势，因此， LAR模型更能有效的应用于基于NIR光谱的果品品质分析中。