基于LPP的工业过程故障检测*

王小卉

（岭南师范学院机电工程学院 湛江 524048）

1 引言

随着现代化工厂生产的不断发展和科学技术的进步，生产设备的生产效率越来越高，机械结构也日趋复杂，因此现代工厂中的控制对象普遍具有惯性大、非线性、强耦合和延时高的特点［1］。

对于实际的过程控制系统而言，很难建立精确的数学模型［2］；而基于定性经验知识的方法需要很多复杂高深的专业知识和期累积的经验，这超出了一般工程师所掌握的范围［3～4］。因此，基于数据的故障检测方法也越来越受到关注。

在过去的几十年里，许多多元统计过程监控的方法［5～7］，例如主成分分析法、因子分析法、独立成分分析法等得到了发展，这些方法进行故障检测主要包括以下几个主要步骤。

1）采集系统正常运行过程的数据；

2）对数据进行预处理和降维，通过一定的置信参数计算距离测度和设置一个合理的阈值；

3）在同一系统中采集一组新的测试数据，计算新的距离测度，判断其是否发生故障；

4）计算每个监控变量对故障的贡献值；

5）鉴别出导致故障发生的根源。

在多元统计过程监控中应用最广泛的为PCA，经过几十年的发展，已经取得了一些突出的成果。PCA的主要思想是在特征空间中寻找一组新的变量来降低原始数据空间的维数，从而从大量的过程数据中获得有用的信息。例如，2017年，张志振等人利用基于神经网络主元分析方法（PCA）对工业中的间歇过程进行故障诊断［8］。同年，杜振宁等采用小波包分解和PCA的结合方法解决传统特征提取方法在非线性特征提取和非线性关系可视上不足的缺点［9］。

但这些降维方法都存在着一个通用的问题，即这些算法在降维的过程中是利用数据的全局信息进行降维，不仅使得算法对异常点很敏感，而且忽略了数据点之间的局部邻域结构信息，使得监测效果降低。

因此，本文采用一种流形学习降维算法-LPP，将其用于工业过程的故障监测。

2 算法介绍

2.1 PCA算法介绍

PCA算法的目的是寻找一组正交基底，使得在新的特征空间里主成分方差最大，并且主成分之间两两正交。假设一个已经去中心化后的数据集其中 n 表示数据集的样本数，m表示数据集的变量个数，即系统的维数，去中心化后的数据集Z的均值为0，方差为1，目的是消除不同量纲对结果造成的影响。PCA是用来寻找一个正交矩阵P∈Rn×l，其中l＜m，其转换方程可以表示为

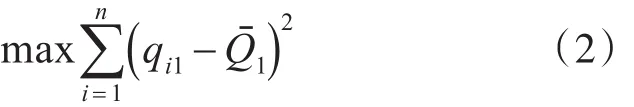
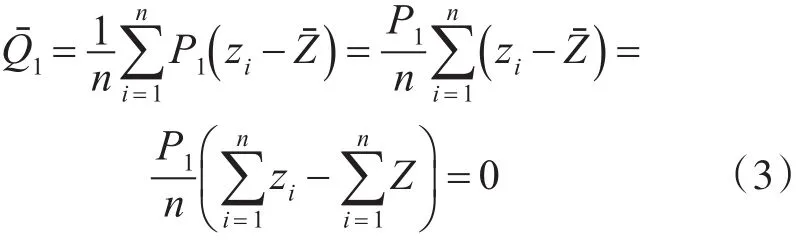
则式（2）可以简化为

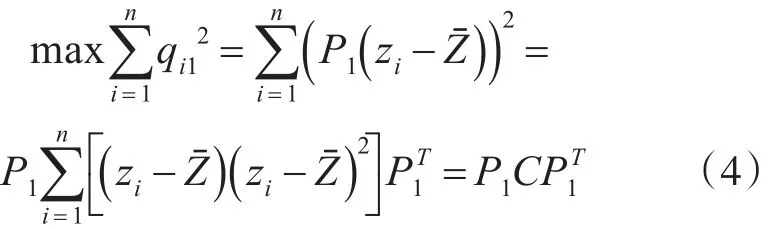
其中C表示协方差矩阵，为了满足正交基底的模为1，以及方便算法的运算，对目标函数加上一个约束条件

那么这个最优化问题同样可以转化为求解式（6）的广义特征值问题。

当第一主成分求解出来后，其他主成分的求解过程同式（2）～（6）。有关PCA算法的具体介绍可以参考文献［10～12］。从PCA算法的求解过程来看，降维后的数据是通过全局分布方差最大来得到的，忽略了数据的局部结构特征。

2.2 LPP算法介绍

LPP算法主要是通过线性近似LE（Laplacian Eigenmaps），算法的本质是一种流形学习方法，其思想是对数据进行特征降维的同时，保持数据的局部结构特征不变，即在高维空间中相距较近的点映射在低维空间中也相距较近，在高维空间中相距较远的点映射后在低维空间中也相距较远［13］。

假设一个去中心化后的数据集 X={x1，x2，…，xn}∈Rm×n。LPP的目的是寻求一个投影转换矩阵A，使得高维空间中的数据集X映射到相对较低的特征空间F∈Rd×n，其中d＜m，其转换方程可以表示为

其中，Y表示投影后的数据集，并且Y={y1，y2，…，yn}∈Rd×n，A是转换矩阵，利用转换矩阵 A投影后的数据集满足下列公式：

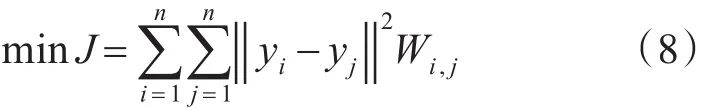
其中，J表示该目标函数，W∈Rn×n是一个权值矩阵，它代表了两个样本点 yi与 yj之间的关系，该权值矩阵的元素可以通过式（9）来确定：

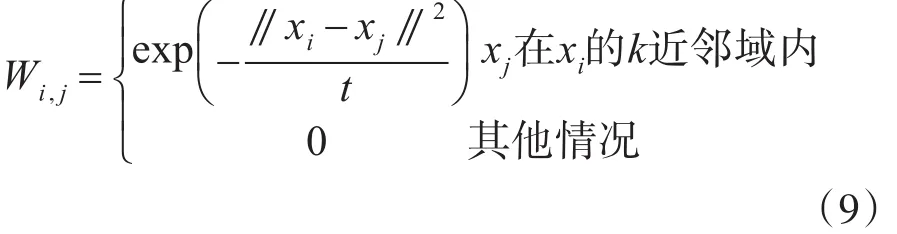
其中，t表示热核参数，t＞0。从式（9）权值矩阵W可以看出，对于两个相距较远的样本点其权值矩阵值为0，两样本点相距越近，其相应的权值矩阵越大，投影后的数据点也越近，这样就可以达到保留样本的局部领域结构，则式（8）可以写成：

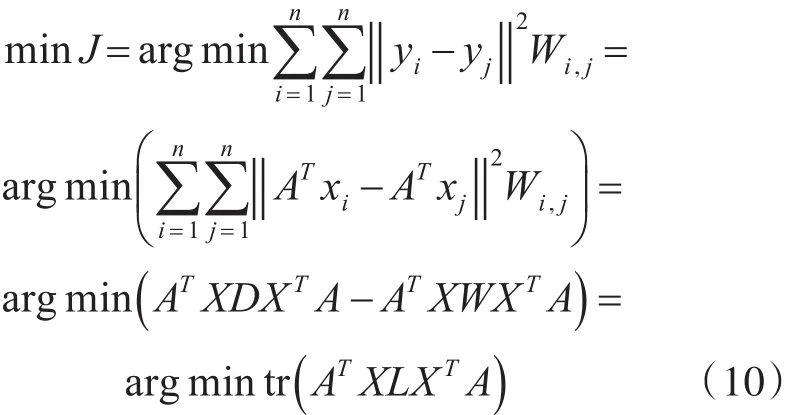
其中，D∈Rn×n是一个对角矩阵，其对角元素L=D-W 为拉普拉斯矩阵，该矩阵的目的是最优化式（10）的解，并且为了防止0向解，引入一个约束条件：

则目标函数式（10）可以写成：

那么这个最优化问题同样也可以转化为一个求解式（12）的广义特征值问题：

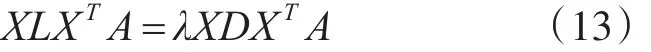
让λi∈R，1≤i≤m表示特征值分解后得到的特征值，βi∈Rm，1≤i≤m表示特征值对应的特征向量，则前d个最小非零特征值对应的特征向量组成了投影转换矩阵A：

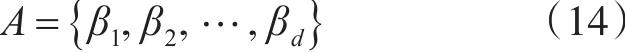
转换矩阵A确定后，就可以得到投影后的数据集Y。通过LPP算法的数学原理过程来看，高维空间中的数据集X可以转化到低维特征空间中，并且通过式（9）的热核参数W使得降维后的数据集依然能够保持高维空间中的局部领域结构。

为了比较两种算法在降维过程中的具体表现，在2.4节将用一个简单的数学仿真模型对两种算法进行对比。

2.3 过程检测方法

当利用正常数据训练出模型后，就可以用多变量统计过程控制图对数据进行监控。目前，使用最多的是平方预测误差（SPE）图、HotelingT2图。其中，T2统计量是度量数据模型主空间波动幅度的指标，SPE统计量是度量数据模型的残差子空间的指标。这两种统计量已在多种复杂的工业过程中得到应用。

T2统计量是模型主分量的标准平方和，表示单个时刻上检测数据样本偏离正常模型的程度。假设LPP算法中，对第i个时刻投影后的变量向量yi∈R1×n的T2统计量定义为

其中，yi是由LPP算法投影后的d个元素组成的向量。显然，T2统计量是由多个变量累计的标量，主要是投影后的模型变量模的波动反映多变量变化的情况。

T2统计量的控制限可以利用F分布按下式进行计算。

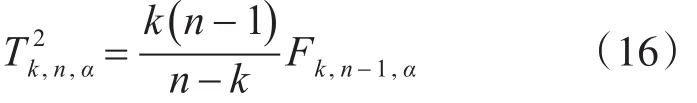
其中，n是样本的个数，k是自由度，即系统的维数，α是检验水平，Fk，n-1，α是对应检验水平为α，自由度为k，n-1条件下的F分布的临界值。

SPE统计量描述的是测量数据投影后的残差子空间变量偏离正常模型变量的程度，则第i个时刻的SPE统计量可以被定义：

其中，yi是正常数据投影后的变量向量，yi_new是测试数据投影后的变量向量。当检测水平为α时，SPE控制限可以被写成：

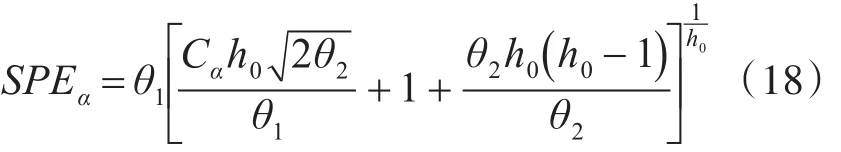
其中

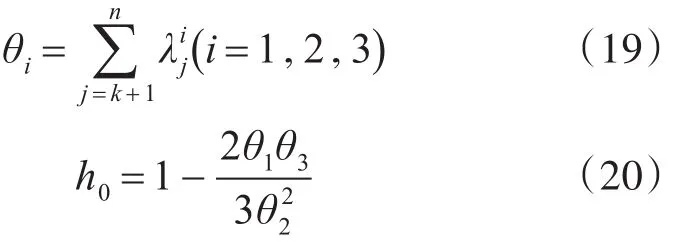
λj表示特征值分解后得到的特征值，Cα时正太分布置信度为α的统计。当两个统计量以及相应的控制限被计算出来后，SPE和T2统计量判断故障发生的规则如下：

2.4 仿真对比

假设一个三维系统的变量分布情况如图1所示。

图1 数据分布图

用PCA以及LPP算法分别对这种类型的数据进行降维，结果如图2以及图3所示。

从图3可以看出，几种颜色类别的点与原数据空间中的点分布情况一致，保留了原有数据空间中的局部领域结构，高维空间中相距较远的点在低维空间中依然相距最远。因此，LPP算法的降维效果比传统的PCA算法更加优越。

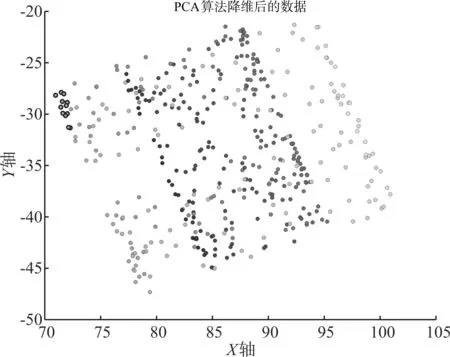
图2 PCA降维结果图

图3 LPP降维结果图

3 仿真实验

为了检验LPP算法检测能力，本章将该种方法应用于TEP仿真平台进行验证，通过在故障检测率（FDR）和检测延时（DL）两个方面和PCA算法的综合比较，来判断所采用的方法的实用性。

3.1 田纳西-伊斯曼系统介绍

TEP是一个真实化工厂的仿真程序，被广泛应用于控制与监控研究，它是一种典型的流程工业过程，有关TEP的运行模式以及生产工艺可以参考文献［14］。图4显示了TEP的五个主要单元的工艺流程图，即反应器、冷凝器、压缩机、分离器和汽提器。整个过程总共产生8个成分，分别表示为A、B、C、D、E、F、G和H。TEP有大量的监控变量，整个系统中含有12个操作变量和41个测量变量。操作变量可看作系统输入，测量变量可看作系统输出。在进行故障检测相关研究时，未加入故障的TEP已经加入了使系统稳定的闭环控制策略，亦即带有一定的稳定裕度。

3.2 数据采集

在TEP的仿真系统中总共采集了53维数据，由于其中有3个操作变量是常数，因此本文只选择了其余的9个操作变量，如表1所示。另外的41个测量变量中包含22个连续过程测量以及19个成分监控变量，有关这些测量变量的具体含义可以参考文献［15］，并且在该文献中介绍了仿真系统中有21中不同的类型的故障，在这些故障中，故障6是唯一一个导致系统停机的，因此只能采集系统运行的部分数据。

图4 TEP过程工艺图

表1 操作变量

在本次仿真实验中，总共采集了960组数据，采样间隔为1s，系统在160s时引入相应的故障。由于故障6导致系统停机，最终只采集到550组数据，并且其中前500组数据是正常数据。

3.3 故障检测性能

为了验证LPP算法的检测能力，比较2种过程检测方法对于TEP的21个故障的统计量检测率（FDR）以及检测检测延时个数（DL），两个检测指标的计算公式可以表示为

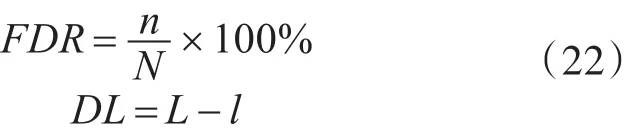
在计算FDR时，N是全部故障数据样本的数量，下载的数据中有960组数据样本，其中有800组故障数据，因此N为800，n是被算法正确检测到的故障样本数量。在计算DL时，L是系统引入故障的数据点，在本章中，系统在第160个样本开始引入故障，因此L为160，l是第一次检测到故障的样本点。故障检测要求是检测算法具有较高的检测率和较低的延时检测个数。最终两种算法的检测结果如表2所示，同时，表2给出了两种算法的故障延时检测个数，表中对于检测率高的值进行加黑加粗处理。

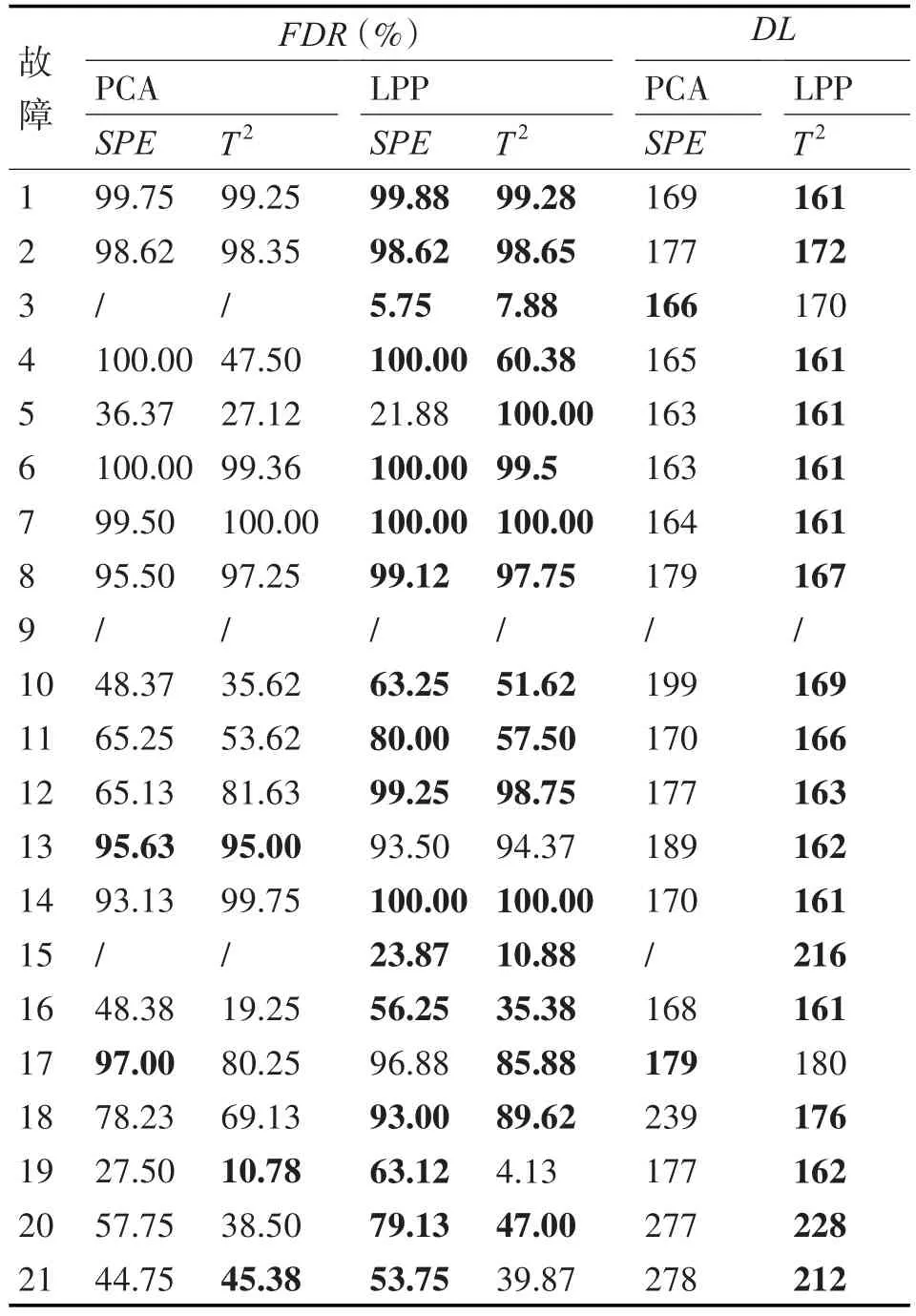
表2 TEP检测算法的检测效果比较

从表2可知，在21种故障中可以看出，故障3、9和15两种算法的检测能力都很低，因为这三种故障发生时，系统变量基本没有发生变化，因此多元统计方法都很难检测到这些故障。此外，LPP算法对于绝大多数故障的检测率均高于PCA，并且在保证具有较高的检测率外，算法的检测延时也很低，说明了LPP算法对于故障更加敏感。值得注意的是，故障5和12，LPP算法的检测效果是明显高于PCA的。图5、6、7和8分别给出了两种方法对于TEP故障5和故障12的检测结果。

故障5为冷却水入口温度的阶跃变化，该变量由于控制回路的补偿作用，即系统存在着负反馈环节，过程会进行动态的调节。从图5可以看出，PCA算法在采样361个数据点后，由于系统的控制补偿作用，整个过程会恢复至正常状态，但是实际过程中，故障5是依然存在的。

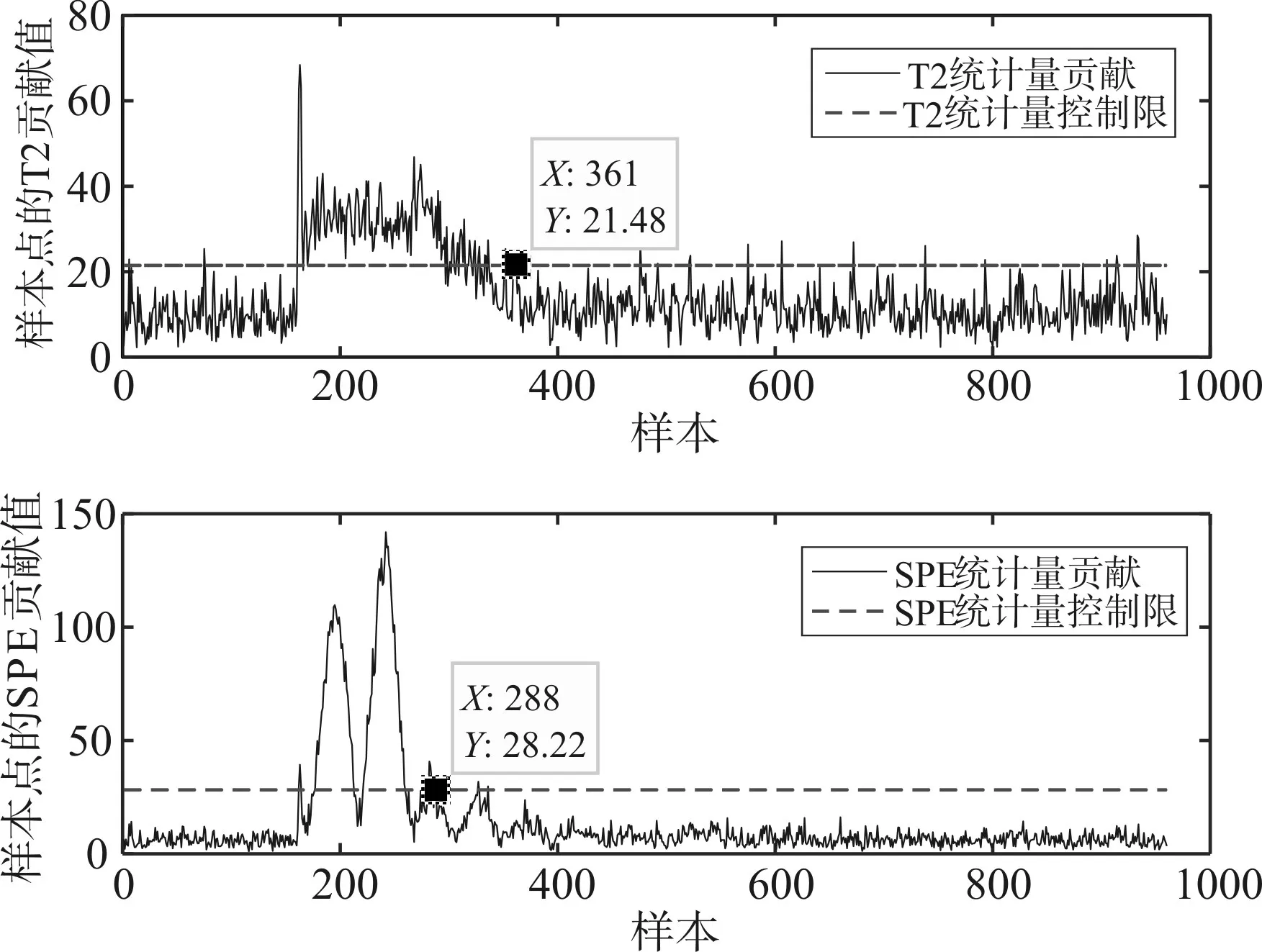
图5 TEP：PCA对于故障5的检测结果

图6 TEP：LPP对于故障5的检测结果

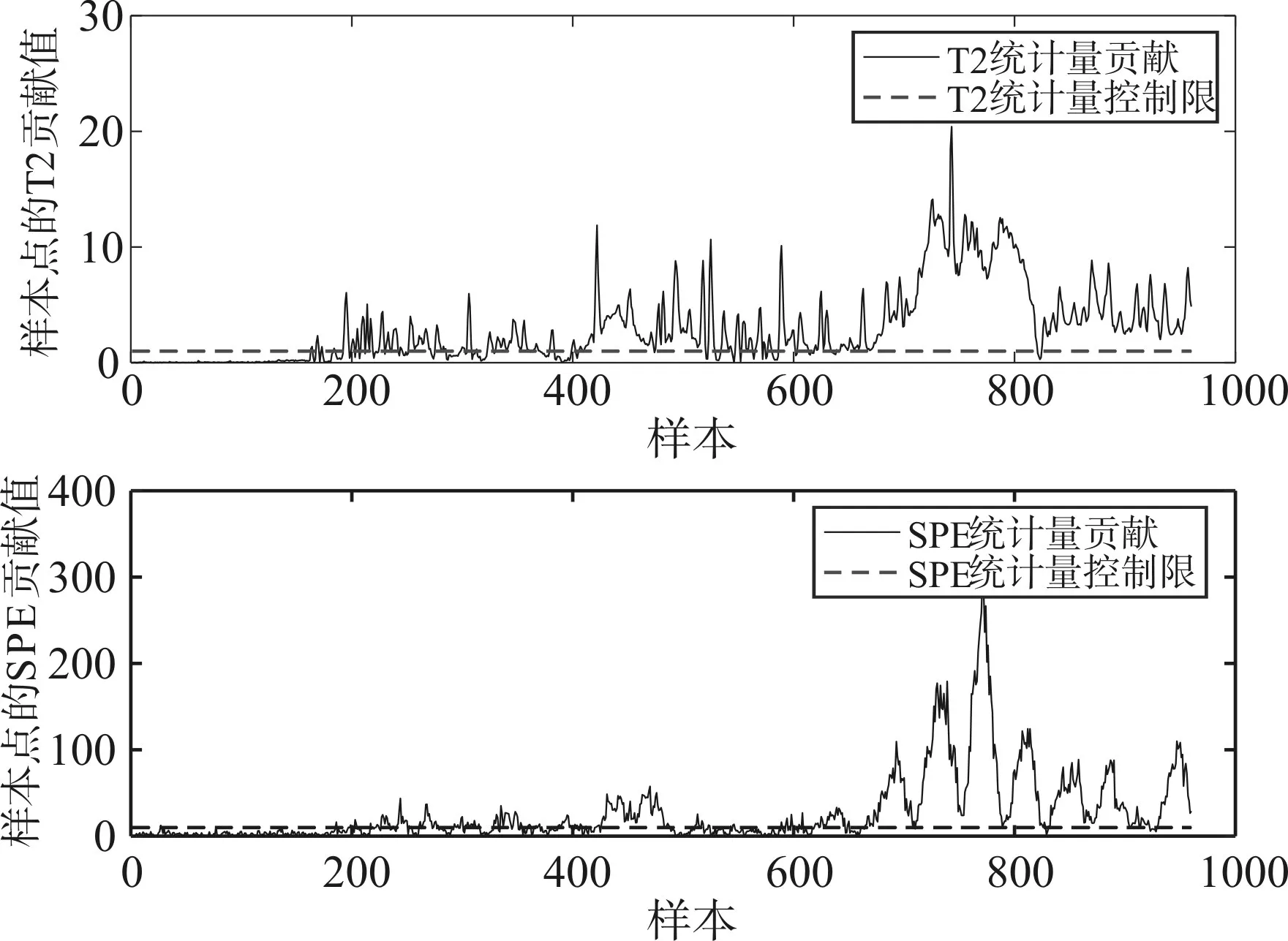
图7 TEP：PCA对于故障12的检测结果

从图6可以看出，LPP算法的T2统计量是够完全能够检测出来的，即通过LPP降维后的主空间变量变化程度是依然超过了阈值的，即使在残差子空间中的SPE统计量在最后同样下降到阈值以下，但依然从T2统计量认为故障是发生的。

故障12是因为冷凝器的进口冷却水温度产生了一个随机变化的影响，因为温度是一个延时性很强的变量加上随机变化的不确定性，当故障发生时，系统整体可能会维持正常运行一段时间，并且系统变量变化不定。从图7可以看出，PCA方法在进行检测时，检测量的值在很多时间段是来回变化的，故最终的检测率不高。但从图8可以看出，虽然LPP算法的统计量同样存在来回波动的情形，但整体的值是没有低于阈值的。因此，LPP算法的检测性能是更加优于PCA方法的。

图8 TEP：LPP对于故障5的检测结果

4 结语

本文针对传统的降维算法如PCA算法，在降维过程中存在着丢失数据的局部邻域信息的问题，采用一种流形算法-LPP对工业工程数据进行检测。首先从数学原理以及简单的数学模型对两种算法进行了比较分析，得出LPP算法不仅可以同PCA算法一样对数据进行降维，而且还能够保持数据的局部领域结构信息，最后将两种方法在传统的TEP上进行验证。

实验结果表明，LPP算法具有更高得检测率以及更低得延时检测，检测性能是优于PCA算法的。