基于多目标优化技术的多源异构数据分类研究*

王维嘉 孙亚运 孙洪亮 范 强

（国网电力科学研究院南瑞集团有限公司 南京 210012）

1 引言

各业务系统建设和实施数据管理过程中，不同存储方式产生的业务数据采用不同的数据管理系统，从简单的文件数据库到复杂的网络数据库，它们构成了企业的异构数据源［1］。异构数据库系统将相关的多个数据库系统进行集合，可以实现数据的共享和透明访问。然而，多源异构数据在分类过程中不可避免地受到数据自身不平衡性的影响［2］。不平衡的多源异构数据分类是数据挖掘和机器学习研究的重点，传统的贪婪搜索监督学习算法［3］通常在不考虑平衡比的情况下进行多源异构数据分类。文献［4］设计的分类模型没有考虑多源异构数据的不平衡问题，并且经过训练的模型由于大量的训练数据而过度拟合，由于缺乏足够的训练（欠匹配），识别少数类测试样本的识别能力极为有限。

本文在多源异构不平衡数据集分类中常用的少数类样本合成过抽样技术（SMOTE）的基础上，提出了自适应多目标群交叉优化（AMSCO），针对多数实例的优化采用群实例选择（SIS），少数实例的优化采用优化合成少数过采样技术（OSOMTE）。最终提高分类模型的可信度并保持较高的准确性

2 SMOTE

最常用的采样方法是少数类样本合成过抽样技术（SMOTE）［5］，它通常可以获得有效的性能，其原理是通过观察和分析少数类样本空间结构的特点，使算法在数据集中生成额外的少数类数据。假设过采样率为N（式（1）合成N次新的少数类样本），每个少数类样本xi∈Sminority。算法使用另一个参数k检验少数类样本中xi的k个邻域，然后利用式（1）从k个邻域中随机选择xt来生成合成数据 xnew，N。

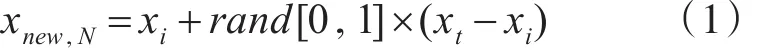
其中，rand[0，1]产生一个介于0和1之间的随机数。通过N和k的影响，得到了合适数量的特征少数类样本。解决训练阶段的分类不平衡问题包含基于集成的技术［6］和对成本敏感的学习方法［7］。集成学习的基本思想是经过几轮迭代，由一系列弱分类器对一个强分类器进行投票和集成。常用的集成学习方法有套袋算法（Bagging）、提升算法（Boost）和随机森林（Random Forest）。过采用（SMOTEBoost）［8］方法结合了自适应提升（Adaboosting）和SMOTE，并且提供了高性能。成本敏感学习［9］通过成本矩阵为混淆矩阵的每个部分分配不同的权重。通常对少数类进行错误分类的成本最大，因此为了得到成本最小的结果，分类器会偏向于对少数类。

3 AMSCO的设计

本文所提出的AMSCO主要使用两个独立运行的群优化过程，分别解决了数据实例过多和数据实例不足的问题。AMSCO的总体思想是对原始数据集进行分解，并仅使用两个群优化过程选择合格实例对其进行重新模拟。首先将原始数据集划分为两组：一组包含纯粹属于多数类的实例，另一组包含纯粹属于少数类的实例。通过群搜索过程，将实例随机编码为表示候选解的搜索粒子，粒子从随机位置迭代移动到全局最优位置。从群进程中选择的实例进行启发式增强，最后只留下一些最合适的实例。

在每次迭代结束时，最合适的粒子表示的合格实例收集到缓冲区中，准备通过交叉操作将它们打包成新的数据集。打包后的新数据集将作为当前数据集，并在新迭代中进行优化。通过这种方式，当前的数据集不断改进其质量，在迭代之后提供了越来越高的适合度迭代。最后，在整个预处理操作结束时，将最精细的数据集输出为最优数据集，从而解决了不平衡问题，最终的数据集可以诱导出性能最好的分类器。中间数据集应该是目前为止每一轮优化中最好的，它由四个可能的数据集组合而成。

四种可能的数据集是优化的多数数据集、优化的少数数据集和当前数据集的三种组合，这四种数据集是要交叉并打包成新一代当前数据集的候选数据集。从图2中，它们混合并列举如下：1）新数据集1=新的多数类数据（在多数实例上经过SIS优化后）+当前少数类数据；2）新数据集2=新的多数类数据（在多数实例上经过SIS优化后）+新的少数类数据（在少数实例上经过OSMOTE优化后）；3）新数据集3=新的少数类数据（经过少数类实例OSMOTE优化后）+当前少数类数据；4）新数据集4=当前多数类数据+当前少数类数据。

本文所提出的再平衡模型的核心是基于群智能优化算法［10］的OSMOTE和SIS算法，该算法迭代地将随机选取的解演化为全局最优解。具体来说，粒子群优化（PSO）算法［11］用于OSMOTE和SIS中，其搜索代理模仿鸟类的飞行模式。假设在D维搜索空间中由 n 个粒子分组的 X=(X1，X2，…，Xn)，该空间中的第i粒子表示为具有D维的向量Xi=(xi1，xi2，…，xiD)T，并且第 i粒子在搜索空间中的位置表示潜在的解。作为目标函数，程序可以计算每个粒子的位置Xi的相应适合度，其中第i粒子的速度是Vi=(Vi1，Vi2，…，ViD)T，每个代理的极值是Pi=(Pi1，Pi2，…，PiD)T，并 且 种 群 的 极 值 是Pg=(Pg1，Pg2，…，PgD)T。每个代理和种群的极值将更新其位置和速度。式（2）和式（3）的数学过程如下：

其中，ω 为惯性权重，d=1，2，…，D ；i=1，2，…，n；k为当前迭代时间；c1和c2为速度因子的非负常数，r1和r2为0～1之间的随机值，Vid为粒子速度。

合作进化是从生态学中的种群协调理论中汲取思想的。它模拟了自然界中不同种群之间的相互影响和相互制约，以增强每个种群和全局搜索的性能。在多种群协作算法中，粒子通过群体间的信息交互随机分为M 个子群Si（1≤i≤M）。有三种评价规则：

适应度定义为精度和Kappa或Kappa统计［12］的乘积。选择Kappa来估计分类模型的可信度。当分类器遇到不平衡数据集时，它具有高精度的标志，但Kappa值很低（零或负值）。Kappa作为指标能够较好地反映测试数据的一致性和分类模型的可靠性，从而考察性能是否属于安全区域［13］。在数学模型中，Kappa结果以步长为0.2的间隔分割在范围为［-1，1］之间的6种不同程度。当Kappa值超过0.4时，模型具有一定的可信度［14］，并且随着Kappa统计量的提高，模型的可信度也会提高。为了表示分类模型的优度，本文定义了可靠准确度（RA）的复合性能准则。因此，适应度函数是由给定数据集生成决策树的性能评估。其他的分类算法可以选择性地代替决策树。适应度RA取决于精度和Kappa，具体定义为

其中，TP、TN、FP、FN、C+和C-分别为真阳性、真阴性、假阳性、假阴性、阳性多数类实例和阴性少数类实例的计数。Po是协议的百分比，Pc是达成协议的机会。

3.1 过采样少数实例的优化（SMOTE）

OSMOTE是由合成的少数实例过采样技术（OSMOTE）［15］扩展得到，通过对少数实例进行过采样来重新平衡数据集。它的基本思想是通过沿着连接数据空间中任意或所有k个少数类最近邻的线段插入合成样本，将额外的少数类数据构建到数据集中。在SMOTE中需要两个参数，并且需要手动设置：1）N的过采样率，其主要控制合成N倍新的少数类样本，例如N=2意味着少数类数据将会增加一倍。2）k对每个少数数据的k个最近邻进行检测，生成合成数据。

本文的OSMOTE方法中，利用PSO优化算法对这两个参数进行优化：1）N表示过采样后数据集的目标量；2）k表示用于复制少数数据向量的参考邻域的范围。PSO群的每个粒子 p都编码为一个候选解，并对应N和k的范围内有一对值p=＜v，κ＞ ，其 中，v∈[1，…，∞]和 κ∈[1，…，(C+，C-)]。适应度函数是由N=v和k=κ的过采样后在数据集上建立的结果决策树。RA性能视为适应度用于评估优度。选择合适的 p使得RA等于适应度的估值。

OSMOTE的目标是提高精度和Kappa，这两个值在搜索过程中动态波动。因此，它是一个动态多目标算法。在不考虑Pareto等复杂情况的情况下，这种对偶目标算法实际上只是试图保持一定的高精度水平，同时实现可信度最大化的Kappa。图1给出了优化过程中精度和Kappa波动的示意图。

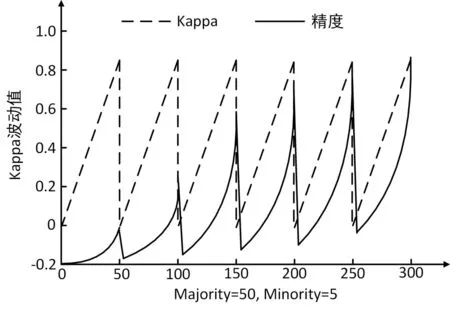
图1 在OSMOTE期间的精度和Kappa波动值

由图1所示，精度和Kappa的趋势相似，但起伏幅度不同，总体呈上升趋势。可以看到，精度和Kappa在第310个迭代周期中都达到了最大值，约为1。由于这两个目标并不相互对立，本文采用非劣集策略［16］进行优化，并针对具体的再平衡任务进行了定制。本文收集了这个多目标问题的所有可能的解决方案。非劣集中的这些解决方案满足三个更新标准来调节OSMOTE的粒子演化、优化和收敛。

1）新粒子的精度和Kappa必须优于现有粒子；

2）新粒子的精度或Kappa必须优于现有粒子，且定义的公差大于F1、ROC、BER等其他测量值的绝对差值；

3）新粒子的当前Kappa阈值必须大于旧粒子的Kappa值。

如果一个新粒子满足上述三个条件中的任何一个，它将取代当前的粒子进入下一代。否则，这个粒子将沿着它的轨迹移动到邻近的位置。该算法通过约束条件的更新逐步提高Kappa。在开始时，Kappa的初始阈值kt设置为0.4，这是Kappa的第二个底部置信水平。在每次迭代的最后阶段，当前非劣集的平均Kappa值将与最新阈值进行比较，如果平均值增加，阈值将进一步增加，反之亦然。随着Kappa阈值的提高，非劣区将逐步减少。搜索空间中非劣区域的说明如图2所示。

图2 搜索空间中非劣区域说明

阴影区域是PSO优化算法的粒子运动搜索空间，粒子群优化算法在其中搜索精度和Kappa的最大值。当非劣区域（搜索空间）被变量Kappa阈值封闭时，搜索时间显著减少。SMOTE的最终目标是找到可靠精度（RA）的最大值，这取决于Kappa和精度。对当前数据集进行搜索的约束是基于如下条件：100 ≤ N ≤ r×Size（majority data，C+）和2 ≤k ≤ r×Size（majority data，C-），其中r是原始数据中多数类和少数类的比例。算法1给出了OSMOTE的伪代码。

算法1 SMOTE的优化（OSMOTE）

指定一个群智能算法A和一个分类器C，初始化A算法和其他相关参数

定义Kappa的下限值：kt

经过调研，由于教师薪酬、院校办学经费等原因，吉林省高职院校旅游管理专业的核心课程教学任务基本上都是由本校教师承担，即使外聘教师，通常也对其学历及职称有要求，这就极大限制了旅游企业在一线实践技能高超的人员走进大学课堂。在师资引进时，各院校对应聘者学历要求是首要考虑的因素，以旅游管理专业博士研究生为主、硕士研究生为辅。从教育规律来看，硕士、博士阶段是以培养科研型人才为主，因此，进入高职院校从事教学活动的教师通常具有极高的科研能力，但是大多没有旅游企业实践经历，其实践技能相对匮乏，这就与高职院校培养高技能应用型人才产生了矛盾。

定义K和N的范围

1：加载数据集；

2：初始化粒子的位置和速度，通过SMOTE和C得到当前的Kappa和精度作为初始的种群适应度；

3：对于i从1迭代到最大迭代次数；

4：Radom从非劣解中选择全局最优解；

5：更新粒子、速度和位置，作为更新条件，新的局部最优替换原来的局部最优；

6：如果粒子满足条件，则改变位置，否则随机选择位置；

7：得到的新旧非劣解集的组合，按更新条件筛选最终结果集；

8：如果没有大于kt的Kappa值，则更新Kappa阈值，减少kt；如果解集中kappa的平均值大于kt加步长，则增加kt；

9：输出：得到最终的全局最佳非劣解。

3.2 减少大多数实例的群实例选择（SIS）

除了OSMOTE可以合成正确数量的少数数据外，群实例选择（SIS）还可以将大多数实例减少到适当的数量。这些优化的输出在其多数和少数类方面进行了重新平衡，这些优化的输出将用作交叉中重组输出数据的潜在候选项。

SIS方法是欠采样方法［17］的进化型，它可以有效地选择有用的大多数样本。由于多数类和少数类数据的不同组合与预测类之间的关系是非线性的。因此，使用分类器来实现大多数实例和少数实例的最佳组合。

考虑到实例的绝对数量，在SIS中，每个PSO粒子将候选解决方案编码为两个部分：1）从当前数据集（如果是第一个周期，则是原始数据集）的大多数实例中随机选择的实例集合；2）从当前（或原始）数据集中少数实例组的全部，与遗传算法［18］中的染色体一样，粒子的集合也会发生变化，从而形成一个由基础学习器最大性能表示的全局最优解。

PSO粒子的大小为size（p）=Random_selection（Datamaj）+Datamin。群粒子的大小受最小和最大限制，分别为Min≥r×Size（Datamaj）和Max＜r×Size（Datamaj），其中r为当前数据集的少数数据与多数数据的比值。图3给出了群实例选择方法的工作过程。

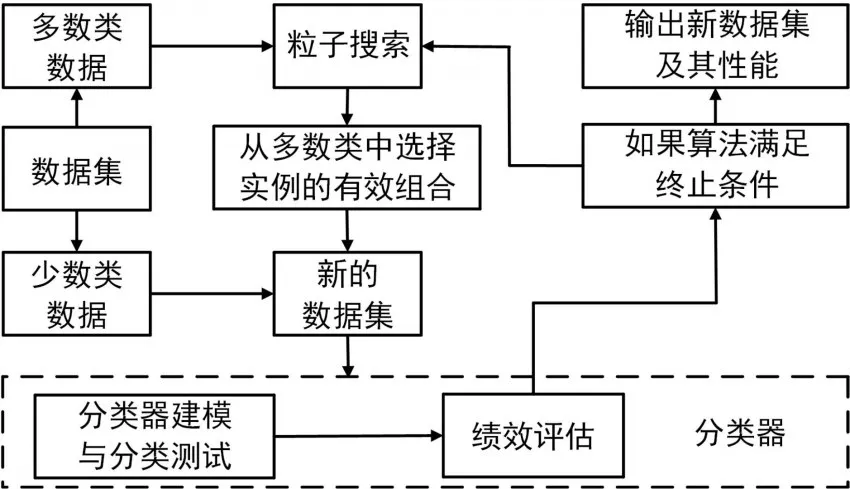
图3 群实例选择流程图

在SIS中，从多数类数据中随机选择的每个组将与所有少数类数据结合创建一个新的候选数据集，该数据集将用于构建用于性能测试的决策树。当SIS运行时，通过比较每个粒子一段时间内的适应度来选择大多数类样本的最佳组合。与其他欠采样方法相比，SIS在计算速度上存在一定的开销。然而，SIS通常可以在最后实现更好的解决方案（全局最优）。算法2给出了SIS的伪代码。

算法2群实例选择（SIS）

指定群智能算法A和分类器C

1：加载数据表；

2：初始化A算法和其他相关参数；

3：数据集通过分类器C得到初始化粒子位置和速度，得到当前可靠的准确度作为初始总体拟合度；

4：从1迭代到最大迭代次数；

5：选择全局最优解，如果当前最优解小于新的最优解，则进行替换操作，否则，继续迭代；

6：随机选择最优解，如果满足最终迭代条件，则结束迭代；

7：输出：获取实例的最佳组合以构建具有其性能的新数据集。

4 实验分析

本文的实验采用了八种平衡方法对所提出的方法与传统方法的性能进行了比较。首先比较了基本分类算法，决策树在没有任何预处理情况下的再平衡，三种方法在算法层面上常用到分类器的偏置，另外四种是采样方法，其中包括传统的过采样方法与三种群再平衡算法。

1）决策树（DT）：在不平衡数据集分类中往往表现出良好的性能。文献［19］对C4.5进行了不平衡数据集的研究，有效地提高了不平衡数据集采样技术的性能。

2）套袋算法（Bagging）：Bagging+DT。

3）AdaBoost.M1（AdaBM1）：AdaBM1+DT。Ada-Boost.M1表示经典的AdaBoost的离散形式。

4）成本敏感（CTS）：CTS+DT。代价矩阵与混淆矩阵、TP和TN的代价元素分别匹配的值为零。FN为误分类的少数类样本，其成本为10。FP为大多数分类错误的样本，其代价为FN的一半。

5）合成少数过采样技术（SMOTE）：SMOTE+DT。使用默认值手动选择这两个参数。其10次运算的平均值作为最终性能。

6）群实例选择算法：SIS+DT。

7）SMOTE优化算法（OSMOTE）：OSMOTE+DT。

8）SIS-OSMOTE：SIS-OSMOTE+DT。这两个优化过程是按顺序放置。当SIS的Kappa大于0.3或达到最大迭代时，OSMOTE将从SIS加载新的数据集。在这种情况下，SIS和OSMOTE可以独立运行，且不需要交叉优化数据集。

9）AMSCO：自适应多目标群交叉优化。

为了公平比较，将 Bagging、AdaBM1、SIS、OSMOTE、SIS-OSMOTE和AMSCO的最大迭代标准化为100。Bagging基础分类器的数量、SIS、OSMOTE、SIS-OSMOTE和AMSCO的种群数设为20。分为10层交叉验证法进行验证和测试。从文献［20］的100个二进制类不平衡数据集中选择30个不平衡数据集用于基准测试。这些数据集的Kappa统计值很低。表1给出了这些数据集的特征，Maj和Min分别表示多数类和少数类，Imb.r表示不平衡比率（多数/少数），且失衡比率从1.87到129.44不等。仿真软件采用Matlab 2014b编写，仿真计算平台采用CPU：E5-1650 V2@3.50 GHz，RAM：32GB。

表1 实验数据集的特点

为了便于比较，将30个基准数据集的平均性能值绘制成直方图，与所有重新平衡算法（群集算法和传统算法）进行对比。研究结果一致表明，AMSCO的表现优于其他方法。图4给出了总体性能比较图。

图4 再平衡方法在Kappa、准确度和可靠准确度比较

从结果中可以看出，在不进行任何再平衡的情况下对原始数据集进行分类的决策树，其精度和Kappa都表现最低。在四种典型的方法中，SMOTE的性能相对较好，AdaBM1优于Bagging。对成本敏感的学习比Bagging更有效。本文使用群的个体类优化方法比传统的方法好得多，证明了群优化的有效性，除了SIS比SMOTE较差。少数数据的OSMOTE比SIS更有效。与传统方法相比，AMSCO的Kappa值在30例中有26例保持在0.9以上，在30例中有3例表现良好。与其他方法相比，AMSCO也相对稳定。精度和Kappa的平均值最高，AMSCO两种性能指标的标准差最低。

5 结语

本文提出了AMSCO算法来处理并行采样两个类时的类不平衡数据集。AMSCO的目标是在合理的时间内重新平衡数据集，以此提高分类模型的可信度并保持较高的准确性。该算法采用两种群优化算法，逐步找出特定分类器的最佳性能：1）将SMOTE扩展为OSMOTE用于将少数数据扩充到适当的数量；2）利用SIS选择有用的实例来过滤大部分数据。实验结果表明，AMSCO在不同类别的再平衡方法中表现出明显的优势。