基于光谱指数和机器学习的土壤有机质含量反演

朱传梅 王宏卫 谢霞 马利刚 仝雁军 古力孜热·买买提

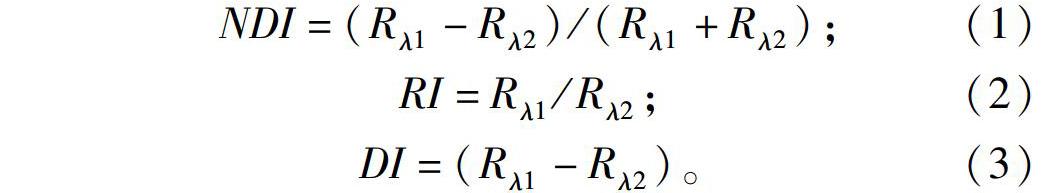
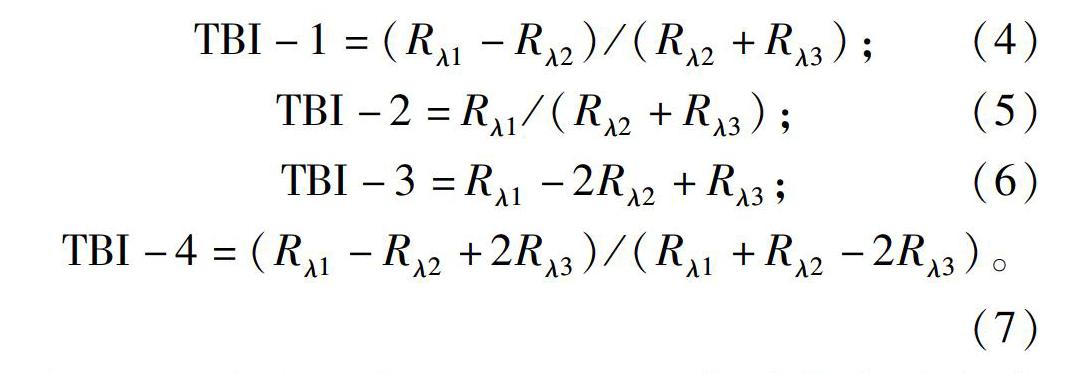
摘要：土壤有机质（SOM）是衡量矿区生态环境质量的重要指标之一。为了提高SOM含量的估算精度，在已有二波段指数的基础上加入第3个波段，构建新的三波段指数，利用极限学习机（ELM）和随机森林（RF）分别建立SOM含量的预测模型。在新疆准东煤田采集168个土壤样点，在室内进行SOM含量、光谱的测定。对光谱数据进行平滑和预处理后，构建多个两波段、三波段光谱指数，随后分析不同维度光谱数据与SOM含量的敏感程度和敏感区域。ELM和RF被用于对每个維度最优光谱参数建立预测模型。研究结果显示，无论采用哪种方式建模，每个维度的光谱数据与SOM含量的敏感程度和建模精度均随信息维度的增加而增加，即三波段指数（TBI）>二波段指数>一维光谱数据。在三波段指数中，ELM的预测效果要优于RF，其中（TBI-4）-ELM的预测效果最好，决定系数（r2）=0.87，均方根误差（RMSEP）=4.07，相对分析误差（RPD）=2.63。三波段指数与ELM的结合，可以很好地减弱土壤信息噪声，提高SOM含量的预测精度。

关键词：遥感;光谱分析;土壤有机质;光谱指数;机器学习

中图分类号：S153.6+21文献标志码：A

文章编号：1002-1302（2020）22-0233-09

作者简介：朱传梅（1993—），女，新疆昌吉人，硕士研究生，主要从事绿洲聚落景观与土壤有机质研究。E-mail：aspiration818@163.com。

通信作者：王宏卫，博士，教授，硕士生导师，主要从事干旱区绿洲聚落生态安全格局与土壤重金属研究。E-mail：wanghw_777@163.com。

矿产资源的开采和加工可以带来更多的经济效益，但是开采煤矿会干扰土层，破坏植被，使土壤失去利用价值，这对土地资源的可持续发展和生态环境构成严重威胁[1]。在我国，大型的露天煤矿多集中分布于干旱、半干旱生态脆弱的地带，该地区土壤自身修复能力极弱，生态敏感性极强，再加上矿产资源长期大量被开采和加工，导致当地环境问题和生态修复问题日益突出[2]。土壤是陆地生态系统中许多生态过程（例如养分循环、水平衡、凋落物分解等）的基础，土壤有机质状态是衡量退化生态系统中生态功能恢复和维持的关键指标[3]。因此，无损地监测土壤有机质（SOM）含量有助于矿区环境管理和生态恢复。一般的SOM含量测定多基于大量的野外土壤采样和繁琐的室内化学分析方法，较费时、费力、耗资，无法满足现代精细农业发展的需要[3]。与传统的方法相比，遥感技术是一种很有前景的土壤属性定量评估方法，具有快速响应、成本低、采集快等特点，可以很好地用来描述、评估不同尺度下表层土壤的各种特征[4]。因此，基于不同的光谱反射和吸收特性，可见光-近红外光谱（VIS-NIR）分析技术可以作为一种替代方法，保证SOM含量的准确估算。

土壤是由多种物质组成的混合物，其反射光谱常包括背景噪声、基线漂移、倾斜等干扰信息，直接用来进行SOM含量的估算得到的结果并不理想[5]。相关研究表明，光谱预处理方法能够较好地移除噪声、突出光谱曲线特征、去除或减弱其他因素的影响，为建立具有较高精度的估测模型提供可能[5]。光谱微分是增加信噪比的主要技术手段之一，其中一阶微分（FD）可去除不同的背景噪声和基线漂移，扩大样本间光谱的差异，反映被测物体的本质特征。连续统去除（CR）法可减小散射对目标光谱的影响，同时可放大微弱光谱的吸收特性[5]。这2种预处理技术被广泛地应用于VIS-NIR分析中，对建立预测能力强、稳健性好的分析模型至关重要。

以往对于SOM的研究是在一维层面（全波段反射率或对应的数学变换）上选取单个敏感波段或多个敏感波段进行建模，该方法仅考虑了SOM与光谱间的关系，并没有考虑光谱间的重叠吸收或相互影响[3-4]。光谱指数是由几个窄波段或宽波段组合而成，可通过分析特定波段间的相互作用，提高对待测属性的敏感程度。Wang等采用最优两波段指数对土壤盐分含量进行分析和预测，取得了较显著的成果[3]。然而，Tian等在水稻叶片氮浓度的定量估测中，对比了两波段指数和三波段指数的估算能力[4]，这些研究和提出的指标表明，通过两波段指数评估某些参数存在不足。对于土壤这种组成极为复杂的物质，两波段指数能否很好地消除或减弱土壤中其他物质产生光的散射和分子的非特征吸收的干扰有待于进一步研究。

机器学习算法在解析非线性问题时表现能力较好，常用于土壤属性的定量化估测，其中，极限学习机（ELM）和随机森林（RF）更是研究的焦点。Douglas等在估算土壤中总石油烃（TPH）含量时，发现与线性偏最小二乘回归（PLSR）法相比，RF模型能更好地反映土壤光谱的非线性响应，从而提供更高的预测精度[6]。然而，ELM和RF能否在较多的土壤信息噪声中（如严重的人为影响）和较低的SOM水平（如干旱区严重的荒漠化影响）下，建立SOM含量和光谱参数的联系，并达到一定的预测精度，有待进一步研究。

本研究的目的：（1）利用波段优化算法，构建新的三波段光谱指数;（2）量化不同维度的光谱参数对SOM的响应;（3）通过比较SOM的预测精度，寻找最有效的建模方法。

1材料与方法

1.1研究区介绍和土壤样本的制备

研究区为准东煤田，位于我国新疆准噶尔盆地东南缘（43°45′～45°00′N，88°45′～91°10′E）为13000km2的露天煤田，煤炭储量预估可达到3900亿t[2]。它是世界上最大的综合煤田，被誉为“中国工业粮仓”。该地为极端干燥的大陆性气候，年平均降水量、温度分别为140～183mm、5.3～7.3℃。土壤母质为第四纪冲积沉积物，地表植被稀疏。准东煤田的主要土地利用和土地覆被类型为荒地、草地、农田等。自2006年准东煤矿启动以来，大量的工矿活动已造成了生态失衡和严重的环境污染，土壤性质可能正在发生变化。

2014年6月，笔者所在研究团队收集了168个土壤样本，期间未发生极端天气（如大雨或强风）。研究区主要地形为丘陵，因此该试验的主要设计路线是沿着道路进行。在确保车辆和人员安全的前提下，选择距离道路较平坦的区域（>300m）作为采样地点。在每个采样点，用木铲收集直径在10m以内的5个子样本的表土样本（土壤深度为0～20cm），并混合成复合样本（质量约1.5kg）。将复合样品立即装入带标签的防水自封袋中，并使用手持全球定位系统（GPS）和植被覆盖率仪记录样品的坐标、高程、植被覆盖率等信息。将样品送回实验室进行室内空气干燥2周（室温26～28℃），小心去除非土壤物质（砾石、植物根、其他物质），然后用玛瑙研钵研磨并通过1.5mm筛，以减小粒径的影响。SOM含量通过重铬酸钾外部加热法[5]进行测定。

1.2光谱数据的采集和预处理

利用ASD地物光谱仪进行土壤样本的光谱采集，该仪器在350～1000nm与1000～2500nm区间的采样间隔分别为1.4、2.0nm，重采样间隔为1.0nm，输出波段数为2151个。土壤光谱的测定应避免外界光源的干扰，因此试验在暗室中进行，选用50W的卤素灯，探头的视场角为5°，探头距离土壤表面30cm，每测定10次进行1次白板定标，每个土壤样本重复测定10次，剔除异常光谱后取其算术平均值作为该样品的反射率。

位于两端（350～399nm和2401～2500nm）处的光谱数据通常存在高频噪声，因此对其进行剔除。对168个土壤样本的400～2400nm反射率光谱进行多项式阶数为2、平滑窗口为9点的Savitzky-Golay平滑。高光谱数据的维数较高，存在的多余重复信息和相邻波段间高度相关。已有文献表明，重采样高光谱数据能够降低信息冗余，提高计算的准确度、速度、反演精度[4]。因此，对光谱数据重采样到10nm，每个光谱由此获得201个波段，降采样后的光谱被定义为原始光谱（R）。

本研究引入了2种光谱预处理方法：用于去除地物背景噪声、修复基线漂移的一阶微分和用于消除散射、突出光谱特性的连续统去除法。预处理工作均在MATLAB2018b中完成。

1.3二维、三维相关系数

相关性分析有助于揭示SOM含量与光谱间线性相关关系的强弱，这种关系通常以一维线性数据的形式展示。近年来，许多研究以可视化的形式展示了常见光谱指数与待测属性的相关关系，该方法不仅将光谱特性从一维扩展到了二维，而且充分考虑了光谱间的相互关系[3-5]，公式如下：

选取特定敏感区域的第三波段叠加在两波段光谱指数上，往往能够增加指数的精确性，增强抗干扰性，清除常用两波段指数存在的易饱和现象等。本研究在所选3种指數的形式基础上增加第3个波段λ3，使用MATLAB2018b做400～2400nm的全波段循环，并选择最优三波段指数构建估测模型。本研究具体涉及如下：

1.4建模预测

为了保证建模集和验证集数据尽可能地涵盖SOM含量的全部范围，本研究使用Kennard-Stone（K-S）算法进行样本集合的划分。该算法根据已选择对象的重要主成分数量来将欧氏距离（Euclideandistance）最大化。168个土壤样本被分成2个部分，其中112个样本用于建模，剩余56个样本用于验证建模结果。

1.4.1极限学习机

极限学习机（ELM）是由Huang等提出的基于单隐含层前馈神经网络的机器算法[7]。与传统的神经网络模型例如反向传播前馈（BP）神经网络模型相比，其学习方式不同，BP神经网络模型利用梯度下降算法，通过反向传播方式进行学习，在学习过程中须要不断地进行迭代来更新权值和阈值。而ELM仅须要添加隐含层节点的个数，利用正则化计算网络的输出权值来达到学习的目的，网络中输入层和输出层的权值和阈值通过随机初始化得到，且不影响网络的收敛能力。因此，它的学习速度比BP等提高了数千倍，且不会出现过拟合现象。

ELM中，连接层的激活函数采用更加接近生物学激活模型的softplus函数代替传统的sigmoid函数，已有在不同数据库的大量实验证明了softplus激活函数具有更好的泛化性能。本研究通过将步长从3增加到150，每次增加3个步长来确定隐含层的最优节点数，每个模型重复50次以减少随机误差。本研究利用MATLAB2018b对Huang等编写的ELM源码[7]进行了部分修改和调试。

1.4.2随机森林

随机森林（RF）是用于分类和回归的一种机器学习算法。RF以决策树学习和简单平均算法为基础，根据每个二叉树上的节点数（m）和自助法（Bootstrap）抽换选取n个样本构建决策树，利用未被选取的样本对每颗树进行预测，由于RF随机选择特征和变量，使模型不容易陷入过度拟合。

为了建立RF模型，对模型中二叉树节点处的变量个数（mtry）和决策树数量（decisiontree）进行调整。选择均方差（MSE）的倒数作为适应度函数值，即最优模型的适应度函数值越小，它与期望值间的误差就越小。mtry以1～9为间隔，每次移动的步长为1，决策树数量以100～2000为间隔，每次移动的步长为100。

1.5模型的精度检验

本研究从拟合程度、估算能力、准确性等3个方面对模型进行验证。模型的拟合度用决定系数（r2）评价，r2越接近1说明模型的拟合程度越好。模型的估算能力用验证集均方根误差（RMSEP）评价，RMSEP越小说明模型的估算能力越好。估算模型的准确性用相对分析误差（RPD）来评价。

2结果与分析

2.1不同的SOM含量和反射光谱曲线

表1显示，168个样点的SOM含量为0.255～45.708g/kg，平均值为7.461g/kg，标准差为8.747g/kg，变异系数为117.23%，为强变异，这表明准东煤矿SOM含量空间变异较大，这可能由不同土地利用方式和人为影响造成的。建模集和验证集间的F-test得出P=0.72>0.05，表明集合的划分比较相似，但差异不显著。

由原始光谱曲线（图1-a）可知，研究区不同SOM含量的光谱曲线形态基本一致，该地区土壤光谱在可见光波段陡峭上升，反射率与SOM含量呈明显的负相关关系，即SOM含量越高反射率越低，土壤光谱曲线在1400、1900、2200nm附近都存在水分吸收谷，在1900nm处较为明显[5]。如图1-b所示，在580、1350、1900nm附近分别出现了不同的正负峰值，可见一阶微分有利于显示原始光谱的部分肩峰。如图1-c所示，反射率经过连续统去除吸收特征得到了明显的放大，其中500、1900nm处的为弱吸收带在连续统去除曲线中可以观察出来，而在反射率曲线中则不明显。

2.2一维相关性分析

由图2可知，R与SOM含量的相关性曲线较为平滑，且没有波段通过0.01水平上的显著性检验，说明R与SOM含量的敏感性较低。然而R经过FD处理后，显著性明显提升，尤其是在640～1110nm处，最大相关系数在840nm处，为0.52，因为该波段附近存在C—H吸收带，与SOM含量直接相关[5]。R经过CR处理后，在1110～1380nm出现了1个相关系数高峰，相关系数为0.3～0.4，使原来弱的吸收特征得到了增强。600、840、2250nm分别为R、FD、CR相关系数绝对值最大的波段，本研究提取了不同处理中相关性最强的波段数据，用于后续的对比分析和估算建模（表2）。

2.3二维相关性分析

图3为基于不同光谱处理得到的两波段光谱指数（NDI、RI、DI）的二维相关系数图，图中横轴代表λ1，[CM（20*2]波长范围为400～2400nm，竖轴代表λ2，波长范围为400～2400nm，右边的颜色轴代表相关系数值到颜色图的映射，颜色轴的上限和下限为最大正相关系数和最大负相关系数。与图2相比，二维相关系数值的阈值范围均大于一维相關系数。其中以SOM含量与CR的差值指数（DI）的相关性为例（图3-i），最大相关系数与（图2）中CR的一维最大相关系数相比提高了0.12。R和CR构建的两波段指数其相关性较好的波段主要集中在可见光和短波近红外区域（图3-a、图3-b），这与Zhang等的研究结果[5]一致。在每个两波段指数中，FD对SOM含量的敏感性最强，其中FD-NDI、FD-DI（图3-b、图3-h）得到的相关系数较大，约为0.55。提取每个指数的最优波段组合并计算其与SOM含量的相关系数，结果列于表2中。

2.4三维相关性分析

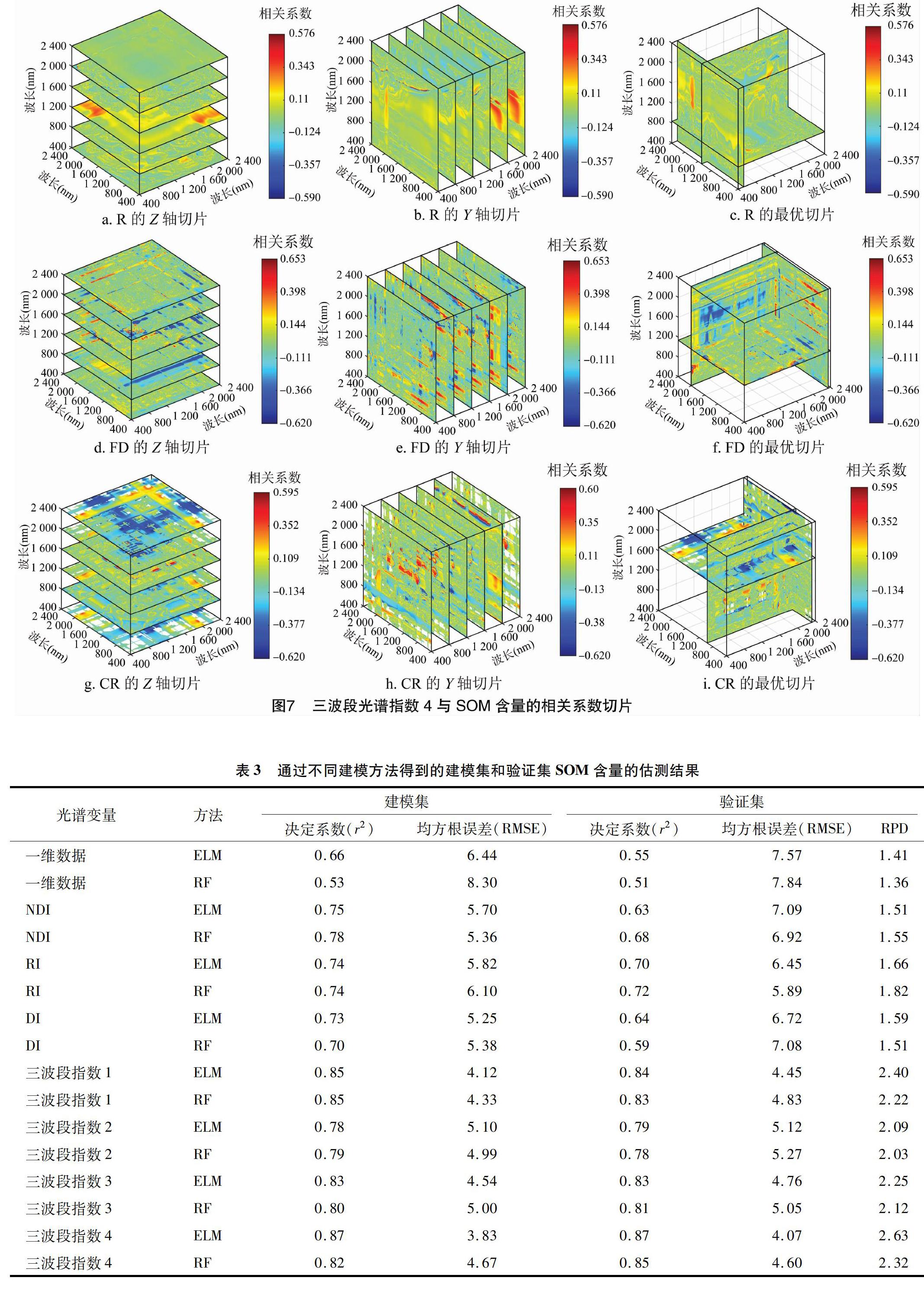
为了充分挖掘光谱数据，根据前人的研究[5]进展，本研究在两波段（λ1、λ2）指数的基础上增加第3个波段λ3，构建新的三波段指数。三波段指数在两波段光谱指数的基础上放大了与SOM含量相关系数的阈值范围（图4至图7）。同时，本研究发现在R所构建的三波段指数中（图5至图7），最优指数的波长基本都在可见光和近红外短波范围内，820～850nm为主要敏感区，已有研究发现820nm附近存在C—H吸收带，这与SOM含量直接相关[5];在FD中（图4至图7），最优指数集中在长波近红外范围，每个指数中均有1个或多个波靠近1450、1950nm的水分吸收带。同时，除TBI-4外，其余3个三波段指数中均有1个波段靠近2300nm，已有研究证明2300nm附近存在1个与SOM含量相关的C—H特征峰[8-9]，在每个三波段指数中，FD的敏感性均最强，但从切片图（图4至图7中的d、e、f）中来看，敏感区域较为分散，不集中;在CR中（图4至图7），780～1100nm的短波近红外为敏感区域，880、950、1020nm为主要的敏感波段，在TBI-2和TBI-3中均有出现。在所有三波段指数中，TBI-4（FD2020，FD2360，FD1150）的效果最优，最大相关系数为0.65，相比于FD的两波段指数（图3-b、图3-e、图3-h）提升了0.1。因此，优化后的三波段指数是估测SOM含量较为有前景的指标，同时也表明两波段指数存在一定的不足。提取每个三波段指数的最优波段组合并计算其与SOM含量的相关系数，结果列于表2中。

2.5建模与预测

利用ELM和RF2种机器算法分别建立SOM含量预测模型，不同维度的最优光谱参数（表2）和建模集中的SOM含量作为机器算法的训练样本（表1），验证集中的SOM含量作为机器算法的预测样本（表1）。

结果表明，无论采用哪一种模型，一维光谱数据的预测效果明显不如多维指数的建模预测结果，r2（0.55，0.51）、RPD（1.41，1.36）较低，RMSE（7.57，7.84）相对较高（表3），虽然ELM的估算精度略高于RF，但该模型仅具有区分样本数据含量高低的能力，量化能力较弱。

两波段指数的建模效果相较一维光谱数据有所提升，r2为0.59～0.72，RMSE为5.89～7.09，RPD为1.51～1.82。三波段指数的估算效果均优于前两者，r2为0.78～0.87，RMSE为4.07～5.2，RPD为2.03～2.63。此外，在三波段指数的建模结果中，ELM对SOM含量的估算能力普遍优于RF。其中使用三波段指数4-ELM的预测效果最好（r2=0.87、RMSE=4.07、RPD=2.63），其拟合程度、估算能力和准确性均优于本研究中的所有模型。

3结论与讨论

光谱指数根据地物的光谱特性，对波段进行简单组合，以达到对地表参量简单有效的度量[10]。前人研究发现由于研究人员自身客观条件的局限性，研究所用的试验数据往往来自某一特定地区，使光谱指数往往具有一定的局限性[11-14]。本研究参考植被光谱分析方法，采用波段优化算法分析了在400～2400nm范围内任意2个波段的NDI、RI、DI与SOM含量间的关系，发现其对SOM含量的响应大大提升。

本研究发现，光谱指数法可在一维线性数据的基础上更为深层次挖掘光谱信息，充分考虑波段间的相互关系和提高建模预测的精度。通过在已有的两波段指数中添加第3个敏感波段，构建新的三波段指数，发现三波段光谱指数放大了与SOM含量相关系数的阈值范围，其中FD的三波段指数4效果最优，最大相关系数为0.65。利用ELM和RF对不同维度的最优光谱参数分别建立预测模型，发现无论采用哪种模型，预测精度均跟据光谱参数维度的增加而增加，并且在三波段指数中，ELM的建模效果均优于RF。其中，三波段光谱指数4-ELM的预测能力最优，r2=0.87，RPD=2.63。该研究结果对减少土壤中其他信息噪声的干扰和土壤属性的定量估算具有一定的参考价值，为估测土壤中其他属性提供了新的思路。

参考文献：

[1]BaoNS，WuLX，YeBY，etal.Assessingsoilorganicmatterofreclaimedsoilfromalargesurfacecoalmineusingafieldspectroradiometerinlaboratory[J].Geoderma，2017，288：47-55.

[2]彭丽萍，戴岳，师庆东.新疆准东荒漠区5种典型植物水分来源[J].干旱区研究，2018，35（5）：1146-1152.

[3]WangXP，ZhangF，DingJL，etal.Estimationofsoilsaltcontent（SSC）intheEbinurLakeWetlandNationalNatureReserve（ELWNNR），NorthwestChina，basedonaBootstrap-BPneuralnetworkmodelandoptimalspectralindices[J].ScienceoftheTotalEnvironment，2018，615：918-930.

[4]TianYC，YaoX，YangJ，etal.Assessingnewlydevelopedandpublishedvegetationindicesforestimatingriceleafnitrogenconcentrationwithground-andspace-basedhyperspectralreflectance[J].FieldCropsResearch，2011，120（2）：299-310.

[5]ZhangZP，DingJL，WangJZ，etal.PredictionofsoilorganicmatterinnorthwesternChinausingfractional-orderderivativespectroscopyandmodifiednormalizeddifferenceindices[J].CATENA，2020，187：104257.

[6]DouglasRK，NawarS，CipulloS，etal.Evaluationofvis-NIRreflectancespectroscopysensitivitytoweatheringforenhancedassessmentofoilcontaminatedsoils[J].ScienceoftheTotalEnvironment，2018，626：1108-1120.

[7]HuangGB，DianHW，YuanL.Extremelearningmachines：asurvey[J].InternationalJournalofMachineLearning&Cybernetics，2011，2：107-122.

[8]史舟，王乾龍，彭杰，等.中国主要土壤高光谱反射特性分类与有机质光谱预测模型[J].中国科学：地球科学，2014，44（5）：978-988.

[9]郑曼迪，熊黑钢，乔娟峰，等.基于综合光谱指数的不同程度人类干扰下土壤有机质含量预测[J].江苏农业学报，2018，34（5）：1048-1056.

[10]张子鹏，丁建丽，王敬哲.基于谐波分析算法的干旱区绿洲土壤光谱特性研究[J].光学学报，2019，39（2）：391-401.

[11]张贤龙，张飞，张海威，等.基于光谱变换的高光谱指数土壤盐分反演模型优选[J].农业工程学报，2018，34（1）：110-117.

[12]尼加提·卡斯木，茹克亚·萨吾提，师庆东，等.基于优化光谱指数的土壤有机质含量估算[J].农业机械报，2018，49（11）：155-163.

[13]章涛，于雷，易军，等.高光谱小波能量特征估测土壤有机质含量[J].光谱学与光谱分析，2019，39（10）：3217-3222.

[14]徐丽华，谢德体.土壤有机质含量预测精度对光谱预处理和特征波段的响应[J].江苏农业学报，2019，35（6）：1340-1345.