输电线路中频融冰频率与热功率均匀度分析

谷文升，汤赐，张承烨，李昭良，陈立君

(长沙理工大学 电气与信息工程学院，湖南 长沙 410114)

输电线路的覆冰会引发线路过负载、绝缘性能降低、杆塔倒塌、导线舞动等事故[1-5]。目前，国内外比较成熟的解决方法主要是基于单相、两相或三相导线短路产生欧姆热的原理，对输电线路进行融冰[6]，此种融冰方法又可分为交流短路融冰和直流短路融冰2类[7]。交流短路融冰可直接利用变电站一次设备提供短路电流，无需额外配置融冰电源，具有技术简单、易于实施、成本低廉的优点；但不足的是融冰无功消耗大、倒负荷繁琐、沿线电流和焦耳热分布不均匀，从而制约融冰效果[8-9]。直流短路融冰与交流短路融冰相比而言，没有诸多不足，只要直流融冰电源容量足够大，则融冰线路长度不受限制，而且沿线电流和焦耳热也分布均匀[10-11]；但其最大的不足是大容量直流电源利用率较低且成本高昂[12]。以上2种主流的短路融冰方法都存在着各自不可克服的缺陷，因此探索新型的融冰技术依旧是当前电力系统的重要课题之一。

2001年，MCCURDY J D等[13]基于在中高频时冰层的介质损耗效应与输电线路的集肤效应均会显著增强的特点，提出了利用60～100 kHz的中高频融冰电源对输电线路进行融冰。当采取适当频率时，结合传输线末端短路时电压电流的准驻波效应，2种热效应将以近似互补的形式实现线路均匀融冰。文献[14-15]分别从融冰原理、临界融冰电流特点、融冰时间长短等方面对高频融冰与交流短路融冰进行了对比分析，得出了高频融冰法具有高效性、临界融冰电流较小及融冰时间短等优点。文献[16]基于高频融冰理论，研究了高频激励下最佳融冰频率的选取、冰层介质损耗角对融冰效果的影响等问题。文献[17]给出了冰层损耗角正切值为0.09时，50 km线路的高频激励融冰电源工作频率和电压，并基于ANSYS进行了电磁-热仿真验证;但是当冰层介质损耗角正切值较小时，所提出的选频方法需要融冰电源频率极高，这会极大增加融冰装置的研制成本，且对线路通信设备造成极大干扰。

本文以长度为100 km，电压等级为220 kV输电线路为例，基于均匀传输线理论和Python程序语言，给出了融冰线路沿线电压、电流和功率因数分布规律；对融冰频率与热功率均匀度两者的关系进行了仿真分析，提出了以牺牲一定热功率均匀度为代价的中频融冰选频方法，在满足全线融冰要求的前提下，可极大降低融冰电源频率。

1 高频融冰线路模型

为简化分析，忽略相邻导线间的相互作用，仅考虑由单根输电导线经由陷波器与大地之间构成的回路，此时覆冰导线模型如图1所示。其中，设导线半径为r，覆冰厚度为t，导线距地高度为h，Cice为导线表面对冰层外表面单位长度电容，C为冰层外表面对地单位长度电容，Gice为冰层的单位长度电导，该参数与冰层的介质损耗角有关。

为方便分析高频时传输线路上的各处电压电流，本文假定线路上各处冰层厚度均匀，即线路各处参数均匀分布，覆冰线路可视为均匀有损传输线，此时覆冰导线的分布参数电路模型如图2所示。图2中:R0为长度为x的导线单位长度dx的电阻，在高频激励下，输电线路的集肤效应使得R0显著增加；L0为线路单位长度电感;ix、ux分别为线路电流和电压。

图1 覆冰导线模型Fig.1 Icing power line model

图2 覆冰线路分布参数电路Fig.2 Distributed parameter circuit oficing power line

上述分布参数的具体计算式如下[18-19]：

(1)

(2)

(3)

(4)

Gice=ωCicetanδ.

(5)

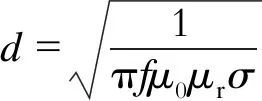
(6)

式(1)—(6)中：σ为导线电导率；d为电磁波在导线中的透入深度；μ0和μr分别为真空磁导率和导体相对磁导率；ε0和εr分别为真空介电常数和冰层的相对介电常数；tanδ为冰层的介质损耗角正切值；f为线路交流频率；ω为角频率。

将图2覆冰线路分布参数电路进行等效化简，得到与经典传输线理论相同的电路模型如图3所示。

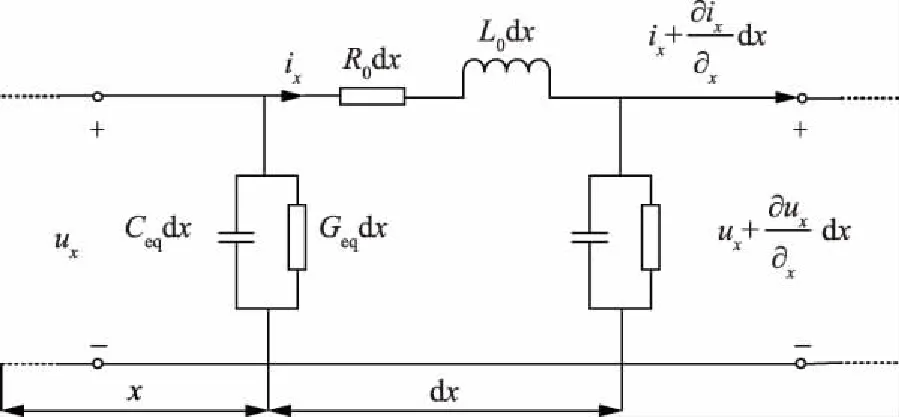
图3 覆冰线路等效电路Fig.3 Equivalent circuit oficing power line

图3中等效电容Ceq与等效电导Geq分别为：

(7)

(8)

(9)

式中：l为需要融冰的线路总长度；γ=α+jβ(α、β分别为γ的实部和虚部)和Zc分别为线路的传播常数和波阻抗，且

(10)

单位欧姆热有效值Pohm、介质热有效值Pdi与合成热有效值Psum的沿线分布关系为：

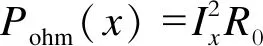
(11)

(12)

Psum(x)=Pohm(x)+Pdi(x).

(13)

式中Ux、Ix分别为沿线电压和电流相量的幅值。

2 融冰频率与电压分析

经过计算仿真，本文发现在中高频电压激励作用下，当线路末端短路时，线路的电压与电流幅值成准驻波分布，相位差为90°；又根据式(11)、(12)可以推论出线路上的单位欧姆热和介质热也成准驻波分布。这样，当融冰电源频率选择为一定数值时，将使2种热效应振幅相同，实现线路的均匀融冰；此外尽可能考虑减小电源的容量，降低融冰装置成本，同时融冰电源频率要尽可能满足功率因数为1。

融冰电源频率的确定可以分为2步：首先根据融冰均匀度要求筛选出符合条件的频率段；然后在该频率段下找出使电源端功率因数最大的一个频率。

本文定义热功率均匀度

(14)

对于有损传输线，当线路末端短路时，结合式(9)，电源端口的输入阻抗

(15)

代入γ=α+jβ对上式进行展开可得

(16)

在中高频激励作用下，传输线路的参数满足ωL0≫R，ωCeq≫Geq(ω为角速度)，所以波阻抗Zc的虚部远大于实部，其幅角接近于0；输入阻抗的幅角主要取决于式(16)的分子部分。考虑当β=kπ/2l(k=1,2,...,n)时，分子的虚数部分为0，则此时始端输入阻抗可视为纯电阻，电源端功率因数为1。

传输线的λ、β与l之间的关系为

(17)

可以推断出，当调整融冰频率使融冰线路长度为四分之一波长的整倍数时，融冰电源的功率利用程度最高。

根据以上的步骤选定好既符合均匀度要求、又使融冰电源利用率最大的融冰频率后，接下来要确定的是使线路各处都能融冰的电源电压。

通常情况下传输线路上保持50 W/m的热功率一段时间就可融化厚度为0.015 m的冰层[13]，即当minPsum(x)≥50时，线路的各处都能达到融冰的功率要求。由式(9)、(10)、(13)可知，Psum(x)是一个关于频率f和电源电压幅值Us的函数，当频率和其他各项参数确定后，只需电源电压保持一定值，即可满足全线路融冰要求。

3 仿真结果分析

本文基于Python程序语言，以220 kV电压等级输电线路为仿真对象，对基于传输线理论的中频激励融冰过程进行理论建模。设融冰线路长度为100 km，导线型号为LGJ-400/50，基本参数取r=0.013 m、t=0.015 m、h=15 m，导线电导率σ=3×107S/m，导线相对磁导率为1，取冰层相对介电常数εr=3。

受气温、气压、杂质含量等诸多因素的影响，冰层的介质损耗角变化范围较大。当施加高频融冰电源时，在几千赫兹到上百千赫兹频率范围内，tanδ位于0.01到1之间[21-22]。

3.1 电压、电流以及功率因数分布

图4给出了tanδ取0.08时电压、电流幅值以及功率因数在沿线的分布情况，此时融冰电源频率为51.15 kHz，电压为23.1 kV。

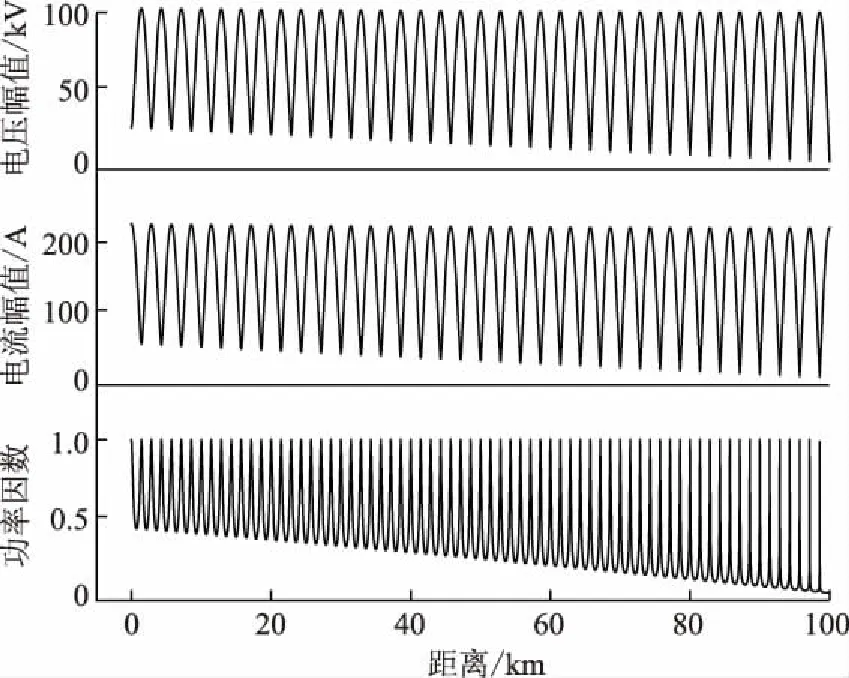
图4 tan δ=0.08时电压、电流与功率因数沿线分布Fig.4 Voltage, current and power factor distribution along the line when tan δ=0.08

由图4可以看出，电压电流幅值在线路上成准驻波分布，并且电压电流相差半个周期。功率因数在输电线路上同样表现出一定的准周期性，即在电压幅值(或电流幅值)波谷和波峰处，功率因数都存在极大值，其值接近于1。此时的融冰电源处功率因数接近100%，能实现融冰电源容量的最大利用；但是为尽可能减轻融冰电源处的绝缘负担，并降低整流逆变单元电力电子器件的复杂程度，应在电压波谷处接入融冰电源，这样能大幅度降低融冰装置的制造成本。

重新考虑式(16)、(17)电源处功率因数为1时线路长度l与电磁波波长λ的关系。当β=kπ/2l中的k分别取奇数与偶数时，输入阻抗可化简为

(18)

3.2 融冰频率与功率均匀度分析

图5—图7分别为tanδ取0.08时，根据不同功率均匀度要求得到的单位欧姆热、介质热与合成热沿线波形。由图5—图7可以看到，沿线欧姆热与介质热两者相位差为90°，恰好形成交替互补效应，最终得到相对均匀的合成热。再参见表1给出的tanδ取0.08时不同热功率均匀度下沿线各项关键参数可以得出：在满足全线路融冰功率均不小于50 W/m的前提下，牺牲一定的沿线热功率均匀度，尽管会抬高沿线最大电压和电流幅值，并小幅度增加融冰电源容量，但仍满足220 kV线路最大允许电压和电流要求，小幅度增加的电源容量也并不会过度影响融冰电源成本；而相比于带来的这些影响，牺牲一定的热功率均匀度能大幅度降低融冰电源频率，从而极大减小融冰电源的研制成本和高频谐波对线路的影响。图5中热功率均匀度为90.62%时，融冰电源频率为51.15 kHz；图6中热功率均匀度为83.58%时，融冰电源频率为40.93 kHz；图7中热功率均匀度为65.43%时，融冰电源频率为23.40 kHz。可以明显看到随着均匀度要求的降低，融冰电源所需频率也随之大幅减小。表2列出的当tanδ=0.13时不同热功率均匀度下沿线各项关键参数，进一步验证了以上结论的正确性。

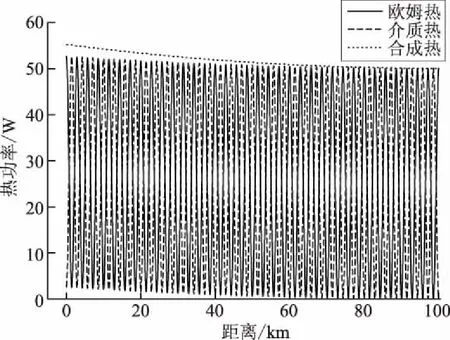
图5 tan δ=0.08，功率均匀度为90.62%时欧姆热、介质热与合成热沿线波形Fig.5 Waveforms of ohmic heat, medium heat, synthetic heat when tan δ=0.08 and thermal power uniformity is 90.62%

图6 tan δ=0.08，功率均匀度为83.58%时欧姆热、介质热与合成热沿线波形Fig.6 Waveforms of ohmic heat, medium heat, synthetic heat when tan δ=0.08 and thermal power uniformity is 83.58%

图7 tan δ=0.08，功率均匀度为65.43%时欧姆热、介质热与合成热沿线波形Fig.6 Waveforms of ohmic heat, medium heat, synthetic heat when tan δ=0.08 and thermal power uniformity is 65.43%

表1 tan δ=0.08时不同功率均匀度下沿线各项关键参数Tab.1 Key parameters of different power uniformity along the line when tan δ=0.08

表2 tan δ=0.13时不同功率均匀度下沿线各项关键参数Tab.2 Key parameters of different power uniformity along the line when tan δ=0.13

表3分别给出了几个不同tanδ时最佳功率均匀度下沿线各项关键参数，此时全线路融冰功率均不小于50 W/m。结合表1—表3数据分析得到：在相近功率均匀度要求下，随着tanδ的增大，所需融冰电源频率与电压逐渐降低，但沿线最大电压与电流也随之增大。所以当tanδ值较小时，沿线最大电压与电流较低、融冰频率过高是主要问题，为降低融冰电源频率，可牺牲一定程度的功率均匀度；当tanδ值较大时，所需融冰频率较低、沿线最大电压与电流过高是主要问题，为保证其满足线路要求，要维持较高的功率均匀度。此外在较高tanδ值时，维持较高的功率均匀度也能降低电源容量，减小装置成本。

4 结论

本文基于均匀传输线理论，对中频融冰分布参数电路进行了理论建模，给出了各分布参数计算式。通过理论计算与仿真，得出以下结论：

表3 不同tan δ时最佳功率均匀度下沿线各项关键参数Tab.2 Key parameters of optimal power uniformity along the line when tan δ is different

a)电压、电流幅值和功率因数在输电线路上均成准驻波分布，且在电压幅值(或电流幅值)波谷和波峰处，功率因数存在极大值，其值接近于1。

b)由融冰激励在线路上产生的介质热和焦耳热两者相位差为90°，恰好形成交替互补效应；当选取合适融冰频率时，可得相对均匀合成热。

c)输电线路中频融冰最佳电源频率的确定分为2步：①根据不同tanδ值给定不同热功率均匀度要求，即tanδ值较小时均匀度要求低，tanδ值较大时均匀度要求高，并筛选出符合条件的频率段，②在符合条件的频率段下找出使融冰线路长度为二分之一波长的整倍数且满足电源在电压波谷处接入的最小频率。

对于长100 km、电压等级为220 kV且不同的冰层环境下的覆冰线路，通过本文提出的选频方法，施加融冰频率不超过50 kHz，功率因数接近1，总容量约为5.2 MVA的融冰电源，在满足全线融冰要求的前提下，可大幅度降低融冰电源频率，从而极大减小融冰电源的研制成本和高频谐波对线路的影响。