人字闸门底枢摩擦副模拟试验台液压系统分析与优化
徐翔,黄柏军,赵新泽,董江安
人字闸门底枢摩擦副模拟试验台液压系统分析与优化
徐翔,黄柏军,赵新泽*,董江安
(三峡大学 机械与动力学院,湖北 宜昌 443002)
为研究人字闸门底枢摩擦副运行时的摩擦磨损情况及主要影响因素,根据相似性设计并建造了液压驱动式模拟试验台。调试过程中发现闸门运行时抖动厉害。为减小闸门的抖动,对其液压系统进行数学建模,并借助Simulink进行动态特性分析。将理论计算结果与试验数据进行对比分析,结果表明:闸门在运行过程中出现抖动是由于在振荡时间内闸门速度发生波动引起的,并且发现闸门的抖动与负载无关,而与流速有着密切的关系;并提出了通过振荡时间内改变流速的方法来减小闸门的抖动,有效地减小闸门的抖动以及抖动的时间。
人字闸门;底枢摩擦副;模拟试验台;液压系统;动态特性
船闸是重要的水路通航建筑物,人字闸门是船闸工程中最常采用的闸门形式之一,底枢则是人字闸门重要的支承运转部件[1]。由于其长期在低速重载条件下启闭运行,加上处于水下,泥沙污染大,磨损状况非常严重。底枢摩擦副一旦过度磨损,就会使闸门体倾斜,从而导致闸门运行不稳定、止水不严等问题。因此,底枢摩擦副磨损失效及寿命预测问题,一直是工程界和学术界关注的焦点。目前在底枢结构的应力分析[2]、摩擦副配对材料研究[3]等方面已取得显著成果。为了更真实的模拟底枢摩擦副的运行工况,深入研究其摩擦磨损机理并进行寿命预测,现以三峡闸门底枢为模拟对象,设计并建造了液压驱动式底枢摩擦副模拟试验台。调试过程中发现闸门启闭时抖动严重。初步分析认为问题出在液压系统部分,现对液压系统的动态特性进行分析与研究。
在液压系统动态特性的分析与研究方面,孔祥东等[4]曾利用Simulink建立了汽车防抱死系统的液压控制单元的模型,并通过试验验证了所建立模型的准确性;陈晨等[5]对新型液压式全可变配气系统的液压系统使用Simulink建立了仿真模型并进行了不同参数下的仿真,提出了改善系统动态特性的方法;杜润等[6]通过对先导式溢流阀的结构和工作原理的研究,得出来先导式溢流阀调整压力的计算方法;孔令喜等[7]对主振机给料装置进行Simulink仿真,得出了主振机的稳态时间、衰减时间以及稳态振幅均随着阻尼比的增大而减小;杨红艳[8]等通过了对进油、回油节流阀节流调速系统进行了数字与实验研究,获得了节流调速系统在不同工作状态下的瞬态特性。
本文根据试验台液压系统图得到每个元件的传递函数,并在Simulink中建立其仿真模型,进行理论分析。将理论分析结果与试验数据相比较,分析闸门在运行过程中出现抖动的原因,提出优化方案。
1 试验台工作原理
摩擦副间的相对速度和接触压力是影响磨损的关键参数[9]。本文以三峡大坝的闸门底枢摩擦副为模拟对象,按照相似原理建立模拟试验台。三峡大坝单扇闸门重达850 t,底枢蘑菇头直径为1 m,蘑菇头帽/蘑菇头间的接触应力达17 MPa。除自重外,人字闸门运行时,还受到风压力、涌浪载荷、动水压力等,为了保证试验台上摩擦副的接触状况与实际运行工况一致,设计试验台加载系统如图1所示,闸门底枢摩擦副模拟试验台的液压系统的工作原理图如图2所示。该试验台的工作顺序为加载-闸门启闭循环-卸载。

(1)加载时,电磁铁YA4得电,液压泵1的压力油通过阀2、3、4、6进入到液压缸7的上腔内,实现液压缸7对闸门的加载。
(2)闸门启闭循环时,保持电磁铁YA4得电,保持加载状态的同时,使电磁铁YA1和YA2交替得电。电磁铁YA1得电时,液压泵1的压力油通过阀2、3、5进入液压缸8的左腔内,活塞杆驱动闸门关闭;电磁铁YA2得电,液压泵1的压力油通过2、3、5进入液压缸8的右腔内,闸门在活塞杆的带动下开启。
(3)闸门启闭循环结束后,对闸门进行卸载,此时电磁铁YA3和YA5得电,其余电磁铁均失电,加载液压缸7上腔中的液压油经过阀6、4回到油箱内,实现卸压。
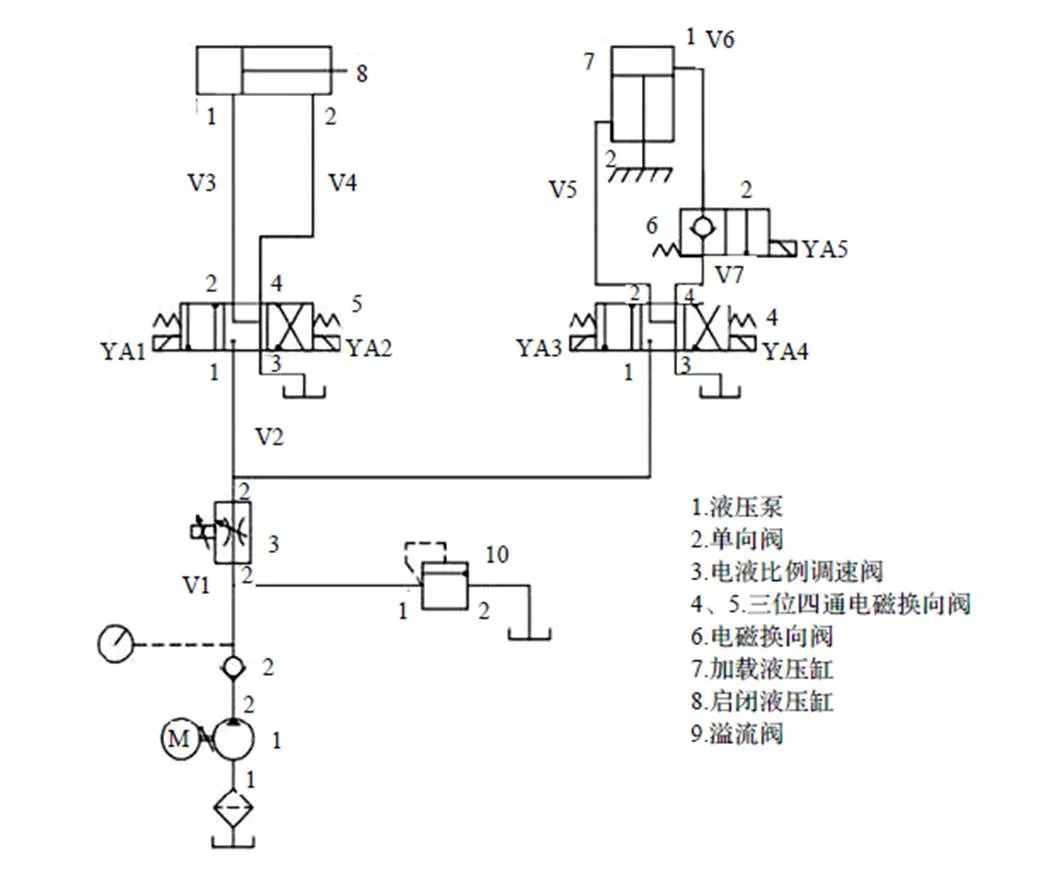
图2 试验台液压系统原理图
闸门运行过程中,由启闭力平衡,可得:
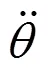
启闭力矩也可用以下公式表示:
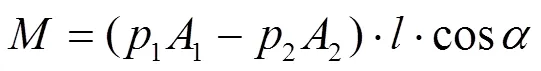
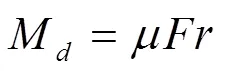
式中:1和2分别为启闭液压缸无杆腔和有杆腔的油压,MPa,可由液压系统压力传感器直接测得;1和2分别为启闭液压缸无杆腔和有杆腔的有效作用面积,m2;M为底枢的摩擦力矩,N·m;为作用在底枢的合力,N;为底枢的最大半径,m;为底枢的平均摩擦系数。
试验台底枢采用45#钢对锡青铜的配副形式,以脂润滑方式进行润滑,故取底枢摩擦系数为0.1,阻尼负载由试验台自身调节,经测量得阻尼负载M=400 N·m。由式(1)可知,通过改变启闭液压缸的进油、出油压力即可改变,其中启闭液压缸的出油口连接油箱,即要改变只需改变启闭液压缸的进油压力。
2 数学建模
建立数学模型的主要目的是预测被驱动负载在控制阀上的输入指令下的速度和位移的响应[10]。由于液压系统是非线性的,因此分析液压系统的动态特性时需要采用集中参数法对非线性模型进行合理的简化。为此,需对系统进行合理的假设:液压泵的驱动速度是定值;由于管路比较短,管路内流动液体的惯量和液阻对负载位置响应的影响可以忽略;滤油器的液阻忽略不计,其液容与液压泵、阀之间的管道
液容合并[11]。
2.1 液压容腔
液压系统是由多个液压元件通过管路连接而成的,且每个液压元件具有多个油口,故一个液压元件可以与多个其它液压元件相连。通过管路相连的多个液压元件之间构成液压容腔。为了建立流量平衡方程,把管路相汇的点定义为节点,通过节点的流量平衡方程来表征节点压力和进出该节点流量之和的关系,即采用容腔节点法[12]。设∑Q是进出容腔流量总和,则容腔压力为:
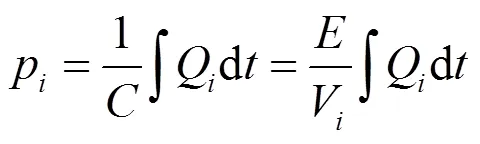
式中:p为节点压力,MPa;Q为节点流量,L/s;V为第个容腔内的容腔体积,m3;为油液的体积弹性模量,MPa;为时间,s。
闸门底枢摩擦副模拟试验台的液压系统根据其液压元件之间的连接可以划分为1~7一共7个液压容腔,同时给液压元件加上油口号用于区分液压元件的不同油口,如图2所示,据此来建立数学模型。
2.2 定量泵
对于定量泵,在忽略液体不可压缩的基础上,还可以忽略泵的移动部分的惯性和内摩擦。已知泵的1油口连油箱,p1为泵1油口压力,则p1=0,泵的特性方程为:
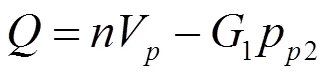
MPa;为泵的驱动速度,r/min;V为排量,mL/r;1为液导,m3/(s·Pa)。
2.3 溢流阀
对于溢流阀除了对其本身进行专门研究时,其余情况下其的动态特性可以忽略不计。
溢流阀的静态特性方程为:
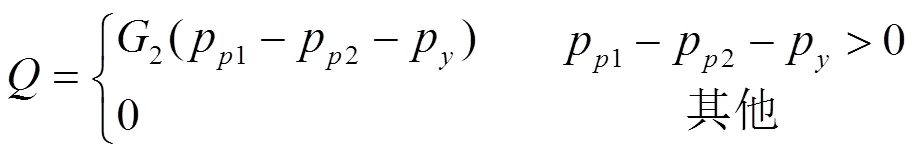
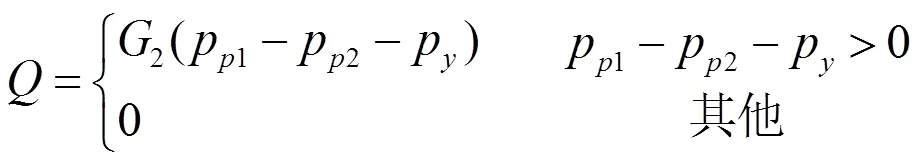
式中:2为溢流阀导通时的液导,m3/(s·Pa);p为溢流阀的调定压力,MPa。
2.4 换向阀
对于换向阀而言,其特性方程可简化为:
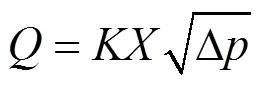
式中:为换向阀阀口综合系数;为阀芯位移引起的开口量,m;Δ为进出阀口的压力差,MPa。
2.5 电液比例调速阀
电液比例调速阀因为其具有控制灵活、精度高、响应快等优点而广泛的应用于工程机械和工程建设机械当中[13],因此采用电液比例调速阀来实现对液压系统的调速,电液比例调速阀的特性方程[14]为:
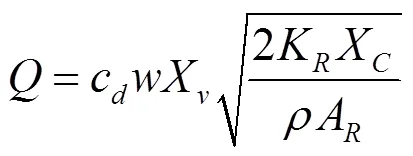
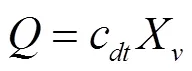
式中:c为调速阀节流口流量系数;为阀芯周长,m;X为调速阀节流阀芯位移,m;为液压油密度,kg/m3;K为调速阀减压弹簧刚度,N·mm;X为调速阀节流口开口为0时的弹簧压缩量,m;A为调速阀减压阀芯最大截面积,m2;c为调速阀的综合流量系数。
2.6 液压缸
根据图2,可以通过以下方程组来表征液压缸的数学模型[15]:
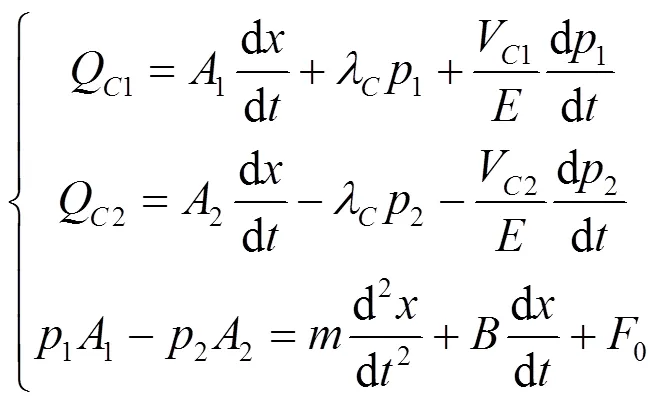
式中:Q1和Q2分别为流进、流出液压缸的流量,L/s;V1和V2为液压缸进油腔、出油腔的容积,m3;λ为液压缸的泄露系数;为黏性阻尼系数;为油液的体积弹性模量,MPa;为活塞位移,m;0为负载力,N。
3 仿真模型
利用Simulink,根据各个液压元件的数学模型搭建试验台液压系统的仿真模型,如图3所示。根据实际选型,各液压元件的相关参数如下:
定量泵的排量V=20 mL/r;额定转速=1450 r/min;定量泵的液导1=2×10-11m3/(s·Pa);加载液压缸型号为HSG100/70-80,无杆腔的有效面积A1=3.2×10-3m2,有杆腔的有效面积A2=1.62×10-3m2;启闭液压缸型号为HSG40/25-480,无杆腔的有效面积1=1.26×10-3m2,有杆腔的有效面积1=7.65×10-4m2;黏性阻尼系数=15680 (N·s/m);漏系数λ=4.47×10-11m3/(s·Pa);运行闸门的总质量=900 kg;油液的体积弹性模量=750 MPa;溢流阀的液导2=2×10-11m3/(s·Pa),溢流阀的调定压力p=10 MPa;换向阀阀口的综合系数=2×105;电液比例调速阀综合流量系数c=0.022 m2,油液密度=900 kg/m3。
仿真时采用Runge-Kutta四阶算法,时间步长设定为0.01 s。
4 仿真结果与分析
4.1 仿真结果实际结果对比
如电液比例调速阀的阀口开启量为X=0.015 m,通过仿真和试验实测,得到启闭液压缸关闭闸门时的速度曲线,如图4所示。
由图4根据仿真的结果以及试验实测数据,可得出当<0.02 s时速度会出现负值;在0.05 s左右闸门速度达到峰值,仿真速度的峰值为0.066 m/s,实测速度的峰值为0.062 m/s,两者误差为6%;随后经过一段速度振荡的时间,仿真速度稳定值与实际速度稳定值均在0.046 m/s左右,仿真速度趋于稳定的时间为0.21 s,实际速度趋于稳定的时间为0.28 s,两者误差为25%。
闸门关闭初始速度出现负值,这是由于液压缸在启动的瞬间液压油被压缩引起的,实测速度曲线的振荡时间比仿真的速度曲线的振荡时间略长,这是由于仿真时忽略了流动液体的惯性和液阻造成的。从上述的数据中可以得出:闸门的抖动时间随着振荡时间的增加而增加,抖动的幅度也随着速度峰值的增加而增加。仿真速度曲线与实测速度曲线运动趋势大致重合,峰值误差不超过10%,趋于稳定时间的误差不超过30%,说明了建立的数学模型以及Simulink仿真模型是合理可行的,可以采用该仿真模型研究该液压系统的动态特性。
4.2 负载力对系统动态特性的影响
在其余仿真参数均不改变的情况下,改变加载液压缸的进油口的压力,得到不同的进油口压力下对系统动态特性的影响如图8所示。
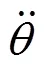
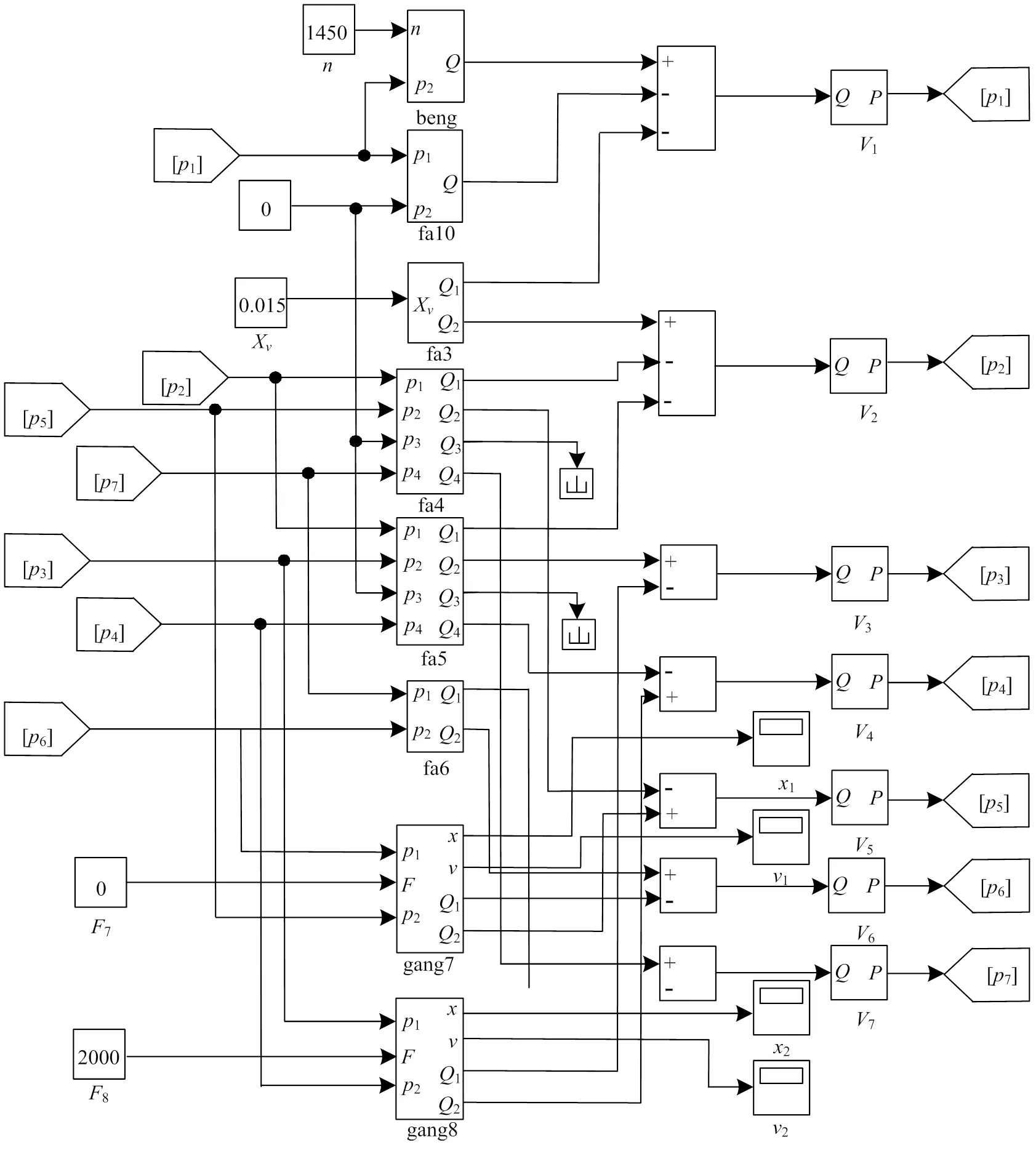
图3 闸门底枢磨损模拟试验台液压系统仿真模型
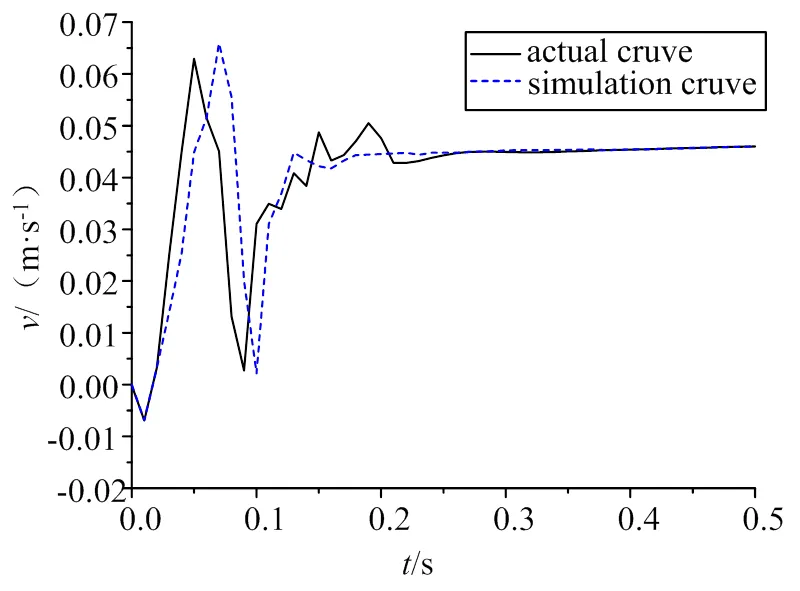
图4 闸门关闭时启闭液压缸速度曲线
4.3 流速对系统动态特性的影响
本试验台以闸门关闭的运动过程为研究对象,通过调整电液比例调速阀阀口开启量的大小来控制液压油的流速,从而控制底枢摩擦副的相对运动速度。从电液比例调速阀的特性方程可得出液压油的流速与阀口开启量的大小呈线性关系,故通过分析阀口开启量的大小对系统动态性的影响即可得到流速对系统动态特性的影响。在其余仿真参数均不改变的情况下,改变电液比例调速阀的阀口开启量,得到不同的阀口开启量对系统动态特性的影响如图6所示。
由图6可知当阀口开启量为0.02 m时,闸门速度的峰值为0.079 m/s,稳定值为0.062 m/s,速度趋于稳定所需的时间为0.24 s;当阀口开启量为0.015 m时,闸门速度的峰值为0.066 m/s,稳定值为0.045 m/s,速度趋于稳定所需的时间
为0.18 s;当阀口开启量为0.01 m时,闸门速度的峰值为0.045 m/s,稳定值为0.035 m/s,速度趋于稳定所需的时间为0.15 s。从上述的数据可得:随着电液比例调速阀阀口开启量的增加,即流速的增加,闸门关闭速度的峰值和振荡的时间均随之增加,导致了闸门的在关闭过程中的抖动幅度和抖动时间也随之增加。
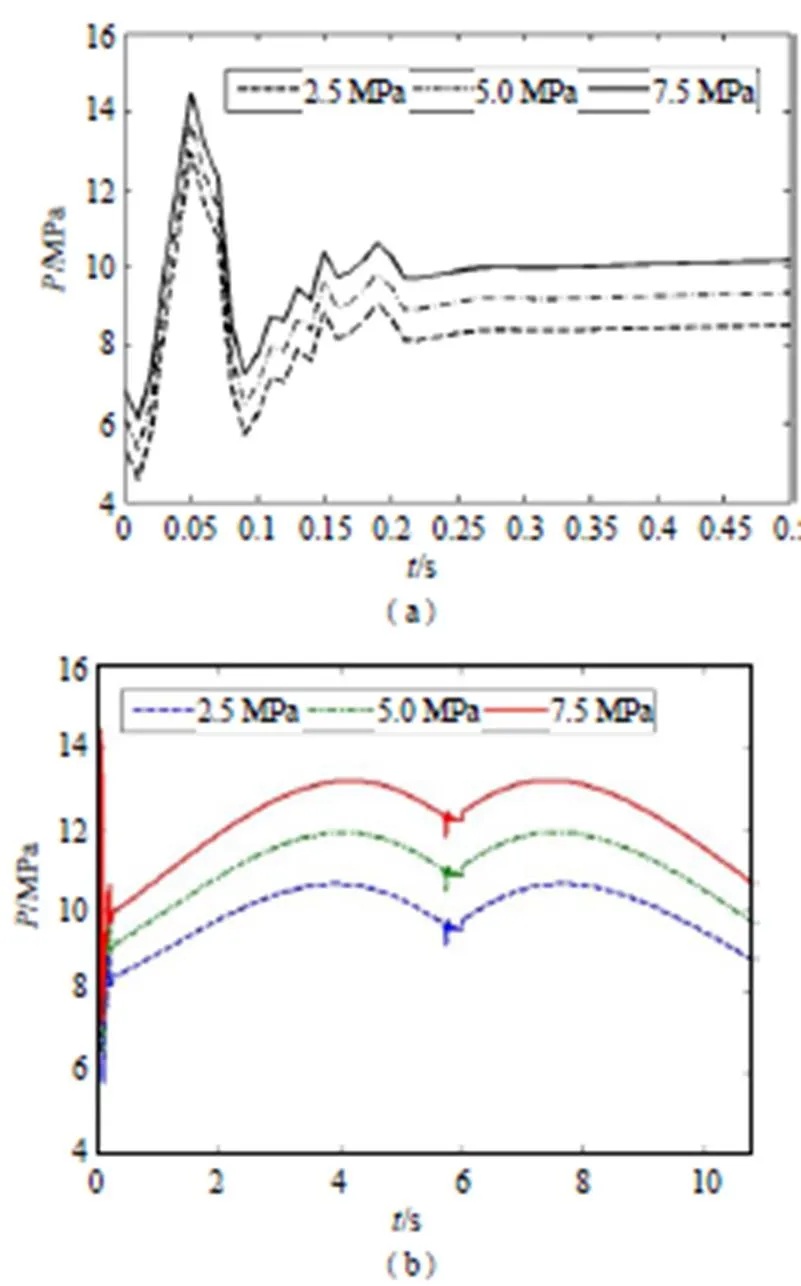
图5 不同进油口压力下的启闭液压缸入口压力随时间的变化曲线图
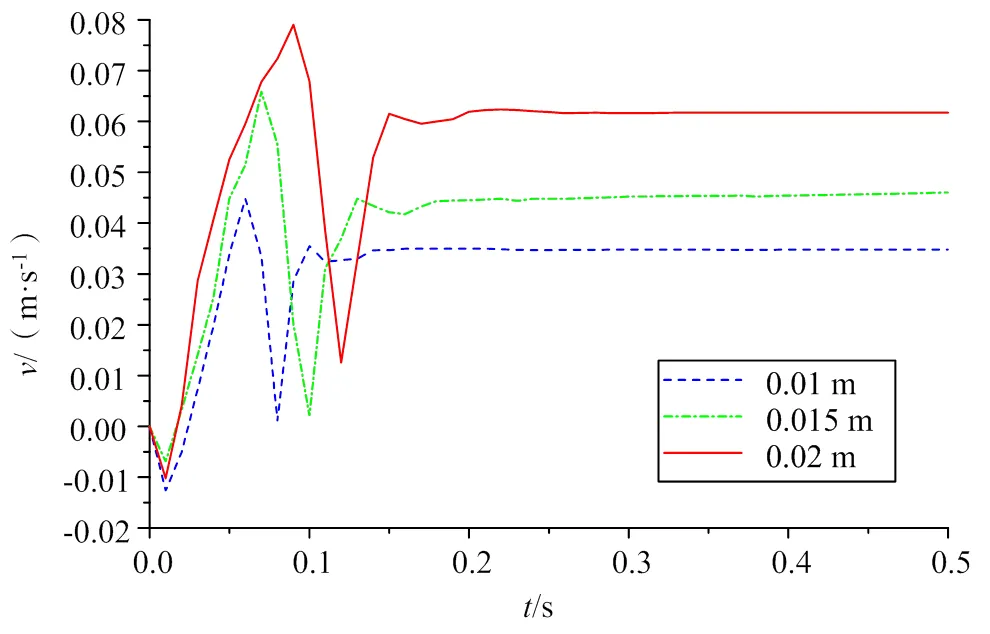
图6 不同阀口开启量下启闭液压缸仿真速度曲线
从对负载力以及流速对系统动态特性的影响的分析中可得,闸门运行过程中出现的抖动现象与负载力的大小无关,而与流速的大小密切相关,因此要减小闸门的抖动,可以通过减小流速来实现,即通过调节电液比例调速阀阀口开启量来实现。
5 优化方案
通过上述分析,只需减小流速即可减小闸门启闭初期的抖动,但是又要保证闸门在稳定运行时以较高的速度运行。因此此处采用先将阀口开启量调到一个较小值,并且在该值对应的振荡时间内再将阀口开启量适当调大的方法,这样既可以减小闸门运行初期过程中的抖动幅度和抖动时间,又能保证闸门在稳定运行过程中以较高的速度运行,则在振荡时间内阀口开启量X的值满足下列条件:
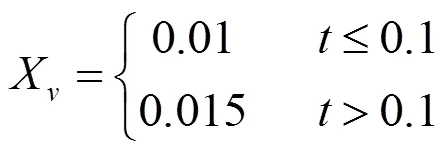
图7为优化后的仿真曲线与当X=0.015 m时的实测速度曲线比较图。可见,优化后在振荡时间内速度的波动幅度总体小于实测值,峰值由0.062 m/s降低至0.045 m/s,降低了27.5%,振荡时间由0.27 s降低至0.15 s,缩短44.5%,两者的稳定值均趋于0.046 m/s。可见:试验台关闭过程中先将阀口开启量调到一个较小值(约0.01 m),并且在该值对应的振荡时间内将阀口开启量适当调大(约0.015 m),既能够有效地减小闸门在运动过程中的抖动幅度以及抖动时间,又能保证闸门在稳定运行过程中以较高的速度运行。
6 结论
(1)建立了闸门底枢摩擦副模拟试验台液压系统的数学模型以及Simulink仿真模型,并将闸门在关闭时的仿真结果与实际运行速度曲线进行比较,结果表明:仿真速度的峰值为0.066 m/s,实测速度的峰值为0.062 m/s,两者误差为6%;随后经过一段速度振荡的时间,仿真速度稳定值与实际速度稳定值均在0.046 m/s左右,仿真速度趋于稳定时间的为0.21 s,实际速度趋于稳定的时间为0.28 s,两者误差为25%,仿真的速度曲线与实测的速度曲线运动趋势大致重合,说明了建立的数学模型以及Simulink仿真模型是正确的,故可以采用该仿真模型研究不同仿真参数下的液压系统的动态特性。
(2)闸门的抖动与负载力的大小并无直接关系,主要受流速的影响。随着流速的增加闸门抖动的幅度以及抖动的时间都会随之增加,故可以通过减小流速来减小闸门的抖动幅度和抖动的时间。
(3)为减小闸门在初期运行过程中的抖动幅度和抖动的时间,并能保证闸门在稳定运行时以较高的速度运行,先将阀口开启量调到一个较小值,并在该值对应的振荡时间内再将阀口开启量适当调大,该优化方法既能有效地减小闸门在运动过程中的抖动幅度以及抖动的时间,又能保证闸门在稳定运行时以较高的速度运行。
[1]顾蓉. 船闸人字闸门底枢摩擦副接触应力分析[D]. 南京:河海大学,2008.
[2]岳陆游,丁建宁,杨继昌,等. 船闸蘑菇头和帽接触有限元计算与优化[J]. 农业机械学报,2006(9):157-160.
[3]刘海,王树林. 船闸底枢摩擦副设计及摩擦学行为分析[J]. 排灌机械工程学报,2015,33(11):960-964.
[4]张晋,孔祥东,姚静,等. 汽车防抱死制动系统液压控制单元的建模与仿真[J]. 中国机械工程,2016,27(21):2967-2974.
[5]陈晨,王自勤,田丰果,等. 基于Simulink的液压系统动态特性仿真研究[J]. 液压与气动,2016(2):67-71.
[6]杜润,杨大治. 先导式溢流阀调整压力分析[J]. 液压气动与密封,2017,37(7):55-57.
[7]孔令喜,张燚,田宝桢. 主振机给料装置的Simulink仿真分析[J]. 机械,2017,44(9):8-11,26.
[8]杨红艳,崔昭霞. 节流调速液压系统动态特性研究[J]. 中国机械工程,2014,25(20):2724-2728,2739.
[9]温诗铸,黄平. 摩擦学原理[M]. 4版. 北京:清华大学出版社,2012.
[10]赵新泽,汪杰,彭巍. 基于Simulink的冲床液压系统建模与仿真[J]. 机床与液压,2012,40(23):161-163.
[11]高钦和,黄先祥. 基于Simulink的重物举升液压控制系统建模与仿真[J]. 机床与液压,2001(1):61-62.
[12]张强,姜毅,傅德彬,等. 基于容腔节点法的液压起竖系统仿真[J]. 机床与液压,2010,38(11):79-82.
[13]张兵,邓子龙. 基于Simulink的比例阀控液压缸的建模与仿真[J]. 机械制造与自动化,2016,45(3):105-108.
[14]杨建峰,王强,王璞. 基于Matlab/Simulink的某电液比例调速阀控同步系统仿真[J]. 机床与液压,2011,39(1):115-117.
[15]赵新泽,彭巍,杨明松. 基于Simulink的镗床液压进给系统建模与仿真[J]. 三峡大学学报(自然科学版),2011,33(3):74-77.
Analysis and Optimization of Hydraulic System of Simulation Test Bench for Bottom Hinges’ Friction Pair of Miter Gate
XU Xiang,HUANG Baijun,ZHAO Xinze,DONG Jiang'an
(CollegeofMechanical&PowerEngineering,ChinaThreeGorgesUniversity,Yichang443002, China)
This paper studies the friction and wear conditions and main influencing factors of the bottom Hinges’ friction pair of miter gate. A hydraulically driven simulation test bench is designed and built according to similarity. However, gate jitter occurs during debugging. In order to reduce the jitter of the gate, a mathematical model of the hydraulic system is proposed and dynamic analysis is carried out based on Simulink. Compared the theoretical calculation results with the experimental data, the results show that the gate jitter during operation is caused by fluctuations in the gate speed during the oscillation time, and that the gate jitter is independent of the load but has a close relationship with the flow rate. Finally the paper proposes a method to reduce the jitter of the gate by changing the flow rate during the oscillation time, which effectively reduce gate jitter and jitter time.
miter gate;bottom hinges’ friction pair;simulation test bench;hydraulic system;dynamic characteristics
U641
A
10.3969/j.issn.1006-0316.2020.01.003
1006-0316 (2020) 01-0015-08
2019-06-26
湖北省技术创新专项(重大项目)(2016AAA076);水电机械设备设计与维护湖北省重点实验室(三峡大学)开放基金(2017KJX01,2017KJX06)
徐翔(1981-),男,湖北鄂州人,博士,副教授,主要研究方向为摩擦学及表面工程。*
赵新泽(1964-),男,湖北潜江人,博士,教授,主要研究方向为摩擦学。

