基于初始条件优化的GM(1，1)幂模型及其应用

丁 松，李若瑾，党耀国

(1.浙江财经大学经济学院,浙江 杭州 310018; 2.浙江省之江青年区域经济与统筹发展研究中心, 浙江 杭州 310018；3.南京航空航天大学经济与管理学院,江苏 南京 211106)

1 引言

灰色预测理论以其在对“贫信息、小样本”特征数据建模拥有独特优势而受到众多学者的关注。GM(1,1)模型和灰色Verhulst模型是灰色预测模型体系中比较重要的两类模型，学者从背景值[1-2]、灰导数[3-4]、参数优化[5-6]、模型外推[7-8]等方面对两类模型进行了一定的优化与拓展，进一步提升了模型的建模效果和应用领域。一般情况下，这两种模型适用于近似灰指数率和灰饱和率的单调小样本序列建模，对于波动性较强序列则束手无策。

GM(1,1)幂模型是GM(1,1)模型和灰色Verhulst模型的延伸，因其幂指数的不确定，可以根据建模数据的特点，如饱和序列、波动序列、高速增长序列等等，借助一定的技术手段，对幂指数进行优化求解，进而对多种特征序列具有很好的适应性和建模有效性，因此在经济社会中得到较广泛应用。邓聚龙教授[9]首次提出GM(1,1)幂模型，但没有给出幂指数的求解方法；王正新等[10]针对幂指数求解问题，借助灰色系统信息覆盖原理首次给出了其求解路径，并讨论了不同幂指数对应模型的极限性质；李军亮等[11]在分析幂模型建立机理基础上，分析了曲线图形与幂指数及发展系数间的关系，利用粒子群算法解出幂指数，取得较好的建模效果。丁松等[12]提出多变量离散灰色幂模型，并给出其参数估计方法和构造驱动控制的灰色幂模型。Hsu[13]分别利用遗传算法优化幂模型的幂指数，并将其应用到电力载荷和集成电路产业预测中，取得了较好的预测效果。杨保华和赵金帅[14]提出了能够表现指数型发展系统和幂函数型发展系统间相互作用关系的离散灰色幂模型，利用参数间的约束关系，构建了离散灰色幂模型初始条件的优化模型，并在中国网络购物人数数据预测中取得较好的应用效果。王俊芳和罗党[15]提出了一种新的分数阶离散GM(1,1)幂模型，借助正则化算法求解参数以消除模型可能存在的病态性问题。为了改善GM(1,1)幂模型的建模精度，王正新、党耀国等还分别从幂模型的无偏性[16]、病态性[17]、自记忆性[18]、时变参数[19]等角度进行了一定的拓展研究，并且在实践应用中获得了众多学者的认可。

上述对GM(1,1)幂模型的改进均是从灰色微分方程的角度加以优化，在一定程度上提升了模型的建模精度，但对于灰色模型求解，初始条件的选取也是影响模型精度的关键因素之一。纵观以往文献的研究可以发现，对于GM(1,1)幂模型初始条件的优化研究主要分为三类，第一类：在以第一个分量x(1)(1)作为模型的初始条件[9]，该方法是传统幂模型的初始条件选择，应用较广泛，其不足主要是选择距离系统趋势较远的初始序列，没有考虑新信息的作用，对于系统未来发展预测可能会存在一定偏差；第二类：Dang Yaoguo等[20]基于“新信息优先原理”，以第n个分量x(1)(n)作为初始条件，一定程度上改善了预测效果，但过度强调新信息对模型建模的影响，忽略旧数据对系统趋势的修正作用；第三类：王正新等[21]以x(1)(1)和x(1)(n)线性组合，作为初始条件，通过构建非线性约束模型对最优组合权重进行求解。该方法一定程度上利用了最旧信息和最新信息，但其对于中间部分的有效信息没有充分利用，对于已经是“少数据、贫信息”的灰色系统建模，势必会对有效信息未能充分提取，造成信息浪费，从而影响灰色建模效果。

因此，本文将在上述研究的基础上，对GM(1,1)幂模型的初始条件进行优化，充分利用旧数据的经验知识和新数据的趋势信息，综合考虑新旧信息间的权重分配关系，实现初始条件最优化。在此基础上，以相对误差绝对值和为目标函数，构建初始条件和幂指数协同优化的GM(1,1)幂模型，利用智能算法或软件进行参数优化求解。最后通过对我国网络购物用户规模预测的案例，对比GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)和PIGPM(1，1,γ)四种模型的优劣。

2 GM(1，1)幂模型及其参数求解

2.1 GM(1，1)幂模型的三种基本形式

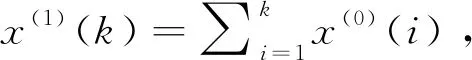
定义1对X(0)，X(1)，Z(1)的定义如上所述，则称灰色微分方程：

x(0)(k)+az(1)(k)=b(z(1)(k))γ,γ≠1

(1)

为GM(1,1)幂模型。

定义2设a为发展系数，b为灰作用量，则称

(2)

GM(1,1)幂模型的白化微分方程。

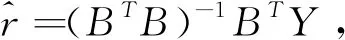
证明：略

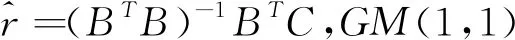
(1)白化方程的时间响应函数表达式为:

(3)在初始条件x(1)(t)|t=1=x(1)(1)时的时间响应式为：

(4)

(3)在初始条件x(1)(t)|t=n=x(1)(n)时的时间响应式为：

(5)

(4)在初始条件x(1)(t)|t=β=βx(1)(1)+(1-β)x(1)(n)时的时间响应式为[21]：

(6)

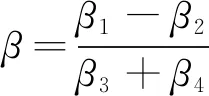
-b/a)e-(1-γ)ak

β4

(5)当k=2,3,…,n时，还原值为

(7)

证明：略

上述为传统GM(1,1)幂模型的建模机理，幂指数γ是未知的，这就使得GM(1,1)幂模型有很大的灵活性去适应高速增长(或递减)、饱和增长(或递减)、波动震荡等多种特征序列。目前，对于幂指数γ求解主要采用两种方法：(1)利用灰色系统信息覆盖思想[10]，借助一阶和二阶灰导数特性对幂指数进行求解，但该方法未以提升模型精度为依据，因此未必能获得较好的精度；(2)借助非线性无约束优化模型，利用LINGO、MATLAB等软件或者智能算法(粒子群、遗传算法等)，实现对幂指数的最优化求解[11]。该方法以平均相对误差最小化为目标，实现建模过程和模型检验标准相一致。定理2中分别给出了目前最常用的三个初始条件下GM(1,1)幂模型的表达式，分别记为GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))和GPM(1,1,β)。

2.2 GM(1，1)幂模型的的幂指数优化

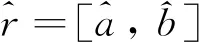
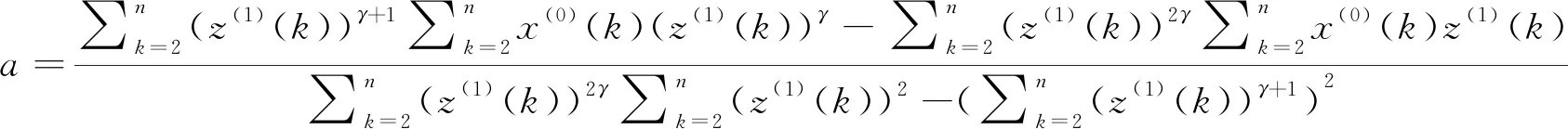
(8)

(9)

为了保证参数优化的目标函数与模拟预测结果检验准则统一，本文以平均相对误差最小化为目标，将幂指数γ与系统参数a和b之间的关系作为约束条件，建立式(10)的非线性优化模型：

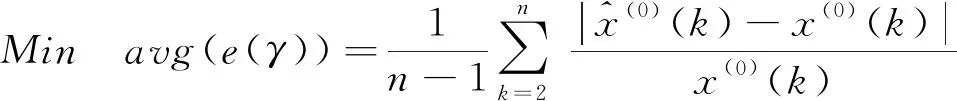
(10)

通过式(10)求解出幂指数参数后，再代入定理1求出系统参数a和b，进而利用定理2进行模拟和预测，实现幂指数最优化的GM(1,1)幂模型构建与应用，记幂指数优化GM(1,1)幂模型为GPM(1，1,γ)。

3 优化的GM(1，1)幂模型构建及参数求解

通过研究众多文献发现，初始条件的选择对于灰色预测模型的精度有着重要的影响，在这部分，将提出GM(1,1)幂模型初始条件的新表达方式，并讨论对初始条件及与幂指数γ的协同优化方法，然后研究时间参数的求解路径。

3.1 GM(1，1)幂模型初始条件优化

实际建模过程中，GM(1,1)幂模型的模拟预测值不仅与第一个分量x(1)(1)或者第n个分量x(1)(n)有关，其应该与X(1)的每个分量都有着密切关系。根据新信息优先原理，新信息中包含了大量系统趋势变化信息，对系统未来发展的认知作用大于旧信息，因而在建模时应赋予新信息较大的权重比例。与此同时，虽然旧信息的有效性在逐渐下降，对未来系统行为的预测作用在减弱，但也不能完全摈弃，旧信息中还存在部分价值数据，具有一定的经验指导作用。因此，如何根据数据序列的实际意义处理新信息与旧信息间的权重分配问题以较为真实地反映权重信息在初始条件构建中的变化规律，是提高灰色建模功效的关键。为了充分考虑新旧信息对预测模型的影响，本文引入权重系数λn-k(0<λ<1)，k=1,2,…,n，以X(1)的每个分量的加权和作为初始条件对GM(1,1)幂模型进行优化，即以

(11)

为初始条件。权重系数λn-k(0<λ<1),k=1,2,…,n随着时间由远及近呈现递减趋势，并且其递减速率与λ取值相关，取值越大，递减越慢，反之越快，如示意图1所示，该图中取k分别取1-10，在λ的不同取值下，权重系数的变化情况描述。该系数一定程度上揭示了一阶累加序列的各分量作用随着时间的往后推移在不断变化，比较贴近实际。权重系数的选择主要与数据序列在现实意义下的递减规律所决定，不是人为设定。从图1中可以看出，X(1)的各个分量的权重满足λk-1<λk-2<…<λk-n，即新信息的权重大于旧信息的权重，并且各分量的作用均被考虑到，既满足新信息优先原理，又充分利用各分量信息。

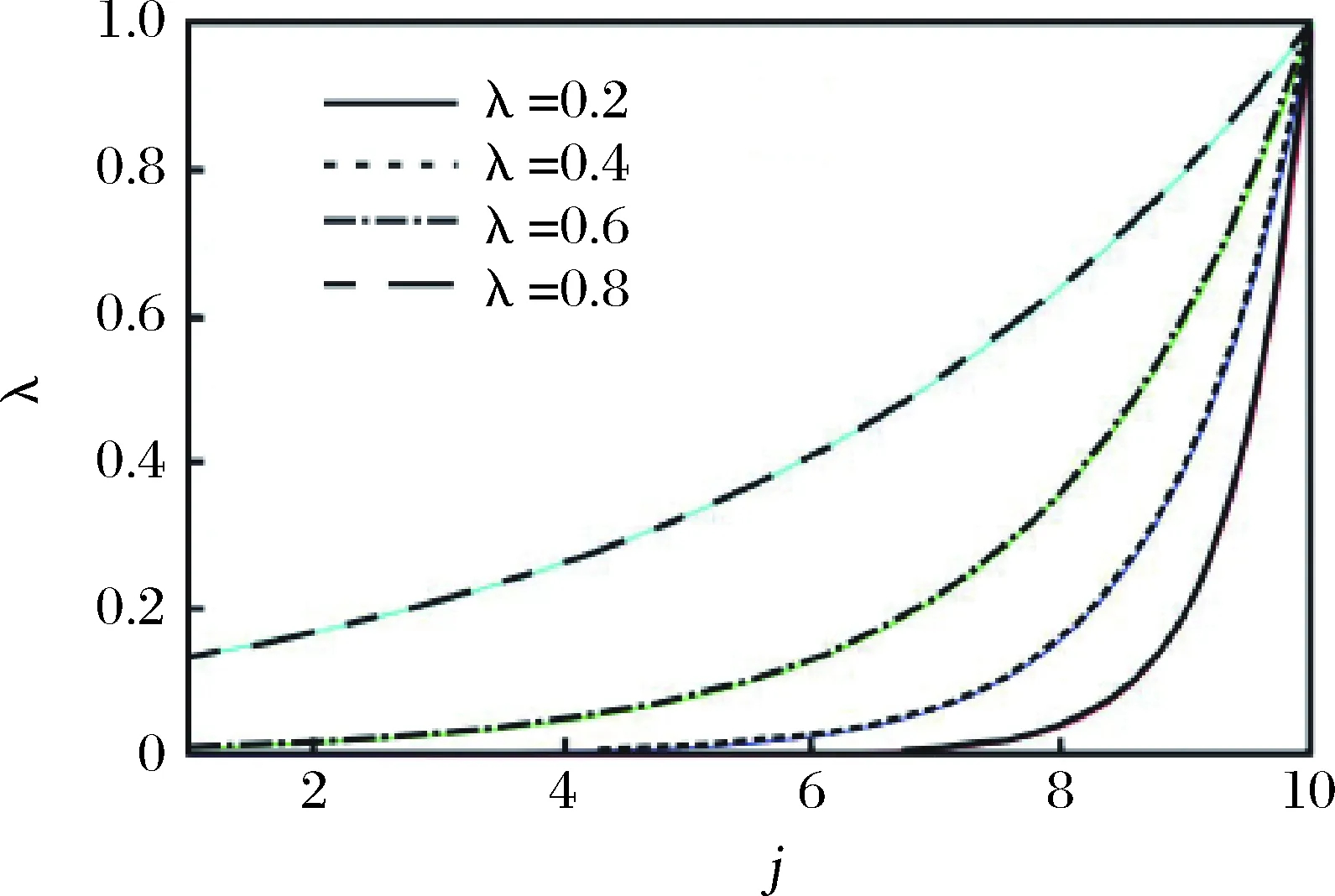
图1 不同λ对应其权重系数递减速率变化

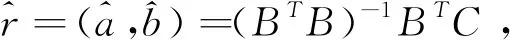
(12)

(2)还原值为

(13)

离散化可得时间响应式为

定理得证。

上述模型称为全信息初始条件优化的GM(1,1)幂模型，记为PIGPM(1，1)( Grey Power Model Based on Perfect Information).该模型能够更好的体现“新信息优先”和“信息充分利用”原理，综合考虑各个变量的变化规律，并将其引入到模型初始条件中，克服了GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))和GPM(1,1,β)的缺陷：分别为对新信息利用不足，过分重视新信息，忽视中间信息的作用。另外，鉴于GM(1,1)模型和灰色Verhulst模型是GM(1,1)幂模型的特殊形式，对于GM(1,1)模型和灰色Verhulst模型也可以采取上述初始条件优化方法，可以进一步提升两种模型的建模精度。

3.2 GM(1，1)幂模型的初始条件与幂指数协同优化建模

通过上述对GM(1,1)幂模型的初始条件优化，我们可以结合幂指数的优化方法，对初始条件参数φ和幂指数γ一并建立优化模型，进而实现初始条件和幂指数的最优解，进一步提升GM(1,1)幂模型的精度。

(14)

通过经典处理软件(LINGO、MATLAB、EXCEL等)或者智能优化算法(粒子群、遗传算法等)可以很方便的对上述模型进行求解，得到GM(1,1)幂模型的模型参数φ,γ,a和b，称初始条件和幂指数协同优化的GM(1,1)幂模型为PIGPM(1，1,γ)。

4 实例分析

目前，中国经济发展已经迎来“中高速增长”的新常态，进入深层次调整期，其关键就是新经济增长点的不断涌现和旧增长点的逐渐淡出。在我国经济增长的“三驾马车”中，消费已经超过投资，成为中国经济增长的第一动力，中国经济的“顶梁柱”。国家统计局数据显示，2015年我国社会消费品零售总额30.1万亿元，同比增长10.7%，消费对GDP的贡献率从2011年的51.6%升至2015年的66.4%。与此同时，传统线下零售业迎来比以往更大的挑战，自2012年以来出现增速连续四年下降，而网络消费却爆发出强劲增长动力，尤其是手机网络购物发展势头迅猛，成为引领消费市场的新增长点。2015年全国网络零售交易额达到3.88万亿元，同比增长33.3%，占全社会消费品零售总额比重持续增长至12.9%。截至 2015 年 12 月，我国网络购物用户规模达到 4.13 亿，较 2014 年底增加 5183 万，增长率为 14.3%，高于 6.1%的网民增速。网购用户规模的快速扩张，网购群体主流年龄跨度增大，有向全民扩散的趋势，为我国网络消费市场的高速发展奠定良好的用户基础，释放着巨大的市场潜力。

随着当下我国“互联网+”、“一带一路”以及一系列有利于促进和保障我国网络购物市场健康稳定发展的战略、政策的出台，我国网购市场的发展远未饱和，市场前景广阔。根据中国互联网络信息中心(CNNIC)发布的2013-2015年《中国网络购物市场研究报告》，本文列出了2006-2015年我国网络购物用户规模的数据，见图2。由图可见，我国网络购物用户规模呈现快速发展的趋势，网购用户占网络用户比重不断上升，从近三年看，网购用户规模增速已经出现减缓势头，整体具有一定的饱和性，即S型增长。因此本文提出的幂指数模型能够较好的描述网购用户规模的发展规律，进而为未来用户增长预测提供一种有效的工具。

在建模数据选择上，本文以2006-2012年我国网络购物人数为建模数据，2013-2015年为预测对比数据，数据见图2。在模型的选择方面，本文选取目前常见的三种初始条件优化的GM(1,1)幂模型和本文提出的基于全信息初始条件优化的GM(1,1)幂模型，分别记为：GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)和PIGPM(1，1,γ)。

图2 2006-2015年网络购物用户规模及渗透率

根据定理2中三种初始条件优化的GM(1,1)幂模型的计算公式可得：

GPM(1,1,x(1)(1))模型：

GPM(1,1,x(1)(n))模型：

GPM(1,1,β)模型：

对于本文提出的初始条件和幂指数协同优化PIGPM(1，1,γ)模型，参数优化结果为：幂指数γ=0.6932，λ=0.1436，φ=7.3872，模型的预测计算公式为：

表1 4种模型的模拟值、预测值及相对误差

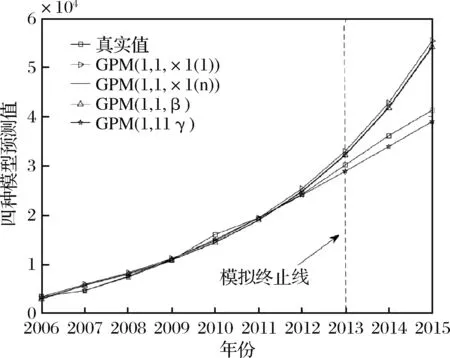
图3 四种模型模拟和预测效果对比图

从表1和图3中可以看出，传统以x(1)(1)为初始条件的GPM(1,1,x(1)(1))模型的模拟和预测误差最大，基本已经失去预测价值，分别达到9.07%和20.64%，高于其他三种模型，主要是因为传统模型在初始条件选取方面未考虑新信息对系统趋势的影响，因此在预测时表现出与真实值较大的差异。对于GPM(1,1,x(1)(n))和GPM(1,1,β)模型，在引入新信息作为初始条件后，其模拟和预测精度有了一定的改善，模拟精度分别提升为8.4%和8.52%，预测精度分别提升为18.17%和17.71%，但是预测误差还是比较大，不适合对我国网络购物用户规模做中长期预测分析。对于本文提出的PIGPM(1，1,γ)模型，在模拟和预测两方面均表现出良好的适应性，精度分别取得了1.68%和5.30%，远远高于其他三种初始条件优化的GM(1，1)幂模型，说明本文在引入权重信息控制参数优化的初始条件具有很好的实际应用价值，充分展示了新旧信息在网络购物用户规模预测模型初始条件构建中的变化规律，既符合了“新信息优先原理”，又符合“信息充分利用原理”，优化的PIGPM(1，1,γ)模型适合作为我国网络购物用户规模的预测。

因此，基于本文提出的PIGPM(1，1,γ)的模型，对我国未来网络购物用户规模进行预测。借鉴新陈代谢的思想，不断利用新数据淘汰旧数据，本文选择7年的数据作为建模数据维度，分别预测下一年的数据，对我国2016年-2020年的网络购物用户规模进行建模预测。模型参数优化结果见表2，2016-2020年间每年的预测建模数据见表3，从表2和表3可以看出，对于预测我国2016-2020年网络购物用户规模模型模拟结果依然保持较高的精度，平均模拟误差维持在区间[0.69%，1.55%]，因此，利用5年的预测公式对2016-2020年我国网络购物用户规模进行预测的可信度比较高。模型的预测计算公式为：

预测2016年网购用户规模公式：

-29122.04)1.11297

预测2017年网购用户规模公式：

-18798.0)1.2164

预测2018年网购用户规模公式：

-35739.0)1.5714

预测2019年网购用户规模公式：

-106977.0)1.0414

预测2020年网购用户规模公式：

-200044.0)0.9924

表2 2016-2020年预测模型的参数优化值

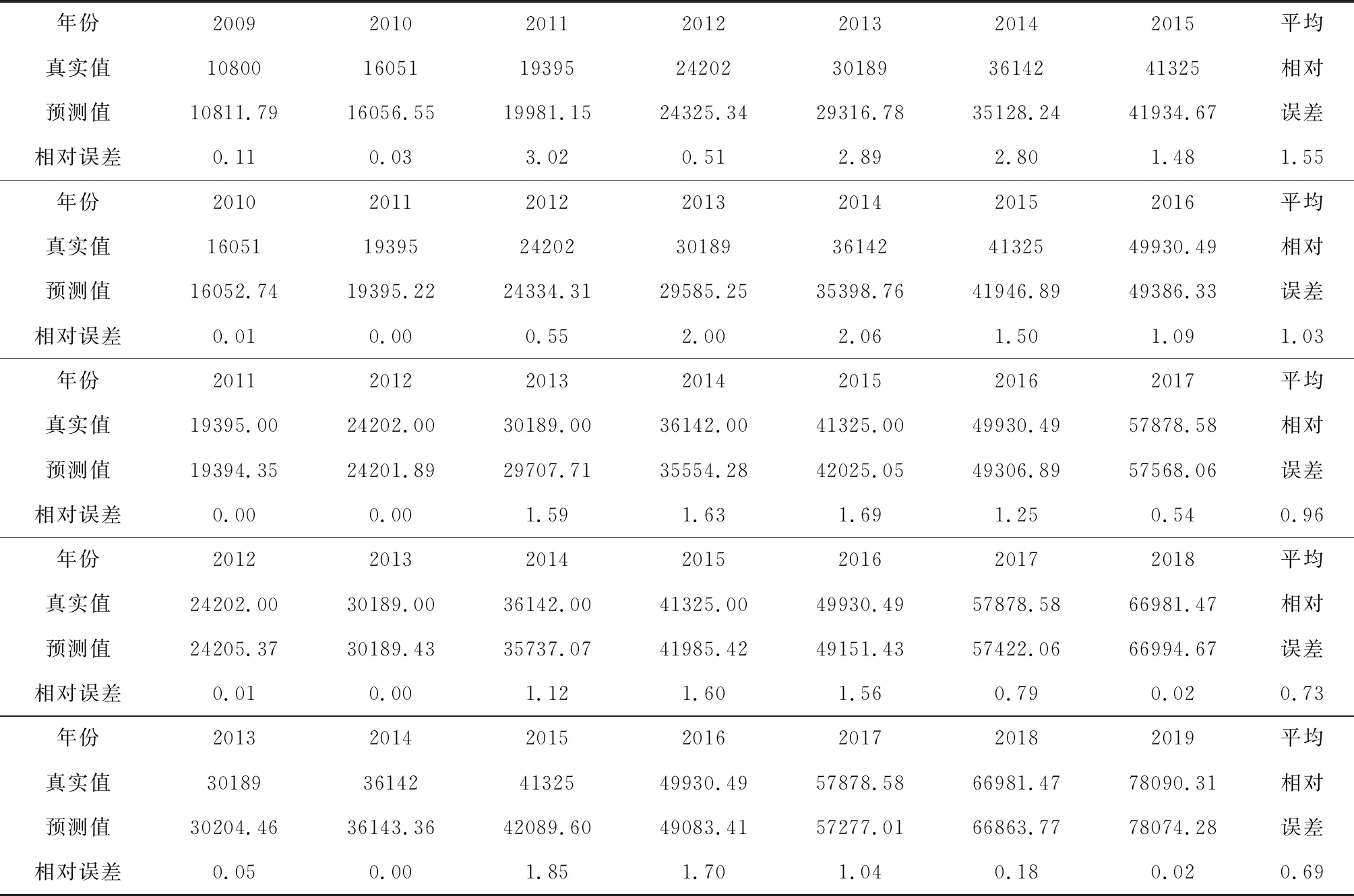
表3 我国未来网络购物用户规模建模数据的模拟值

为了进一步发展网上购物等电子商务的发展，我国已经从多方面展开布局，推动以拉动消费为主的经济发展方式。在宏观政策上，进一步完善“互联网+”顶层设计，促进互联网与传统产业融合，通过电子商务培育经济发展新动力；在发展农村电子商务方面，推动“网货下乡”和“农产品进城”双向流通，从基础设施建设、人才培养、金融支持等多方面促进农村电子商务发展，进一步释放农村居民网络购物消费的发展潜力；在跨境电商方面，通过降低关税、扩大支付限额、提高通关率等政策措施，为跨境电子商务发展提供便利，进一步规范海外网购发展。从见表4可以看出，在众多利好政策的刺激下，我国未来网络购物将会继续保持快速、稳健的的发展趋势。根据中国互联网络信息中心发布的最新《第43次中国互联网络发展状况统计报告》，2016-2018年间，我国网络购物用户规模分别达到46670、53332、61011(万人)，与表4中本文模型预测的结果相比，精度分别为6.99%、8.53%和9.79%，均小于10%，达到较好的预测效果，预计到2020年我国网购用户规模将突破9亿人，可见，网上购物在未来将会成为一种消费习惯，是网民常态化的购物方式。

表4 2016-2020年我国未来网络购物用户规模预测值

5 结语

对于GM(1,1)幂模型，幂指数γ取值的多样性使其能够面向含有多种特征的序列进行预测建模，进而赋予其超越GM(1,1)模型和灰色Verhulst模型更广阔的应用领域。然而其幂指数求解一直是困扰该模型进一步推广应用的瓶颈，本文借助非线性优化方法和工具实现GM(1,1)幂模型的参数优化，是一种改善模型精度的有效方法。

另外，鉴于初始条件对灰色幂模型精度的重要影响，以及新旧信息在初始条件选取方面作用的差异，本文通过设计权重系数控制函数，并结合一阶累加生成序列各时点数据的实际值，构造新型优化的初始条件。该新型优化的初始条件不仅能体现新信息优先原理，更能表现新旧信息作用变化规律。与此同时，利用非线性优化方法协同优化初始条件和幂指数，可以显著地提升GM(1,1)幂模型的模拟和预测精度。

最后，在对我国网络购物用户规模预测实例中，本文提出的初始条件优化模型取得了较好的模拟和预测效果，并结合新陈代谢思想，对2016年-2020年的网络购物用户规模进行预测。通过对比常见的三种优化模型：GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)，模拟和预测结果显示，本文模型在模拟和预测阶段都能表现出良好的建模效果，具有很好的适用性和稳定性。最后，采用本文优化模型对未来2016-2020年我国网络用户规模进行预测，通过收集2016-2018年的真实数据，对比突出本文优化模型的真实预测效果。结果显示，本文模型在实际应用中能高精度预测未来我国网络用户规模的动态变化，预计2020年我国网络购物用户规模将会突破9亿人，网上购物将会成为一种居民生活消费习惯，是网民常态化的购物方式。

单变量灰色幂模型因其特有的幂指数结构而具有对多种特征序列具有较强的适用性，未来将对其多因素影响下的多变量幂模型结构进行研究，并探讨其病态性和稳定性。