归纳推理热点题型展播
景在荣
推理与证明问题综合了函数、方程、不等式、解析几何和立体几何等多个知识点,需要采用多种数学方法才能解决问题,是提高成绩区分度、增强选拔功能的重要题型.因此,在近几年的高考试题中,推理与证明问题成为一个热点题型.归纳推理是由部分到整体、由特殊到一般的推理方法,即归纳推理思想是在解决问题时,从特殊情况入手,通过观察、分析、概括、猜想得出一般性结论,然后进行证明.这一数学思想方法在解决探索性问题、存在性问题或与正整数有关的问题时有着广泛的应用.其思维模式是“观察—归纳—猜想—证明”,解题的关键在于正确的归纳猜想.
1 结论型
结论型归纳推理是指通过对特例的观察和综合去发现一般规律.解题的基本步骤是:先在诸多特例中发现某些相似性,再把相似性推广为一个能明确表述的一般命题.

……
照此规律,当n∈N*时,
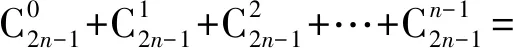


2 周期型
此类问题一般会在周期上设置障碍,要通过周期的定义或有关结论算出已知式子的周期,再进行求值运算,特别是抽象函数,要能够熟练运用赋值法.此类问题往往以函数、数列为载体,考查学生对周期的求解.


S2 018=a1+…+a2 018=a1+a2=3.

3 分组型
分组型归纳推理题目呈现方式为一些有规律的数组,考查归纳推理能力,解答这类问题的关键是明确题意,发现题目中的变化规律.



4 递推型
递推型归纳推理题是依据问题所呈现的数量间的关系或相关规律,辅以一定方法来递推归纳,得出问题的通式,从而探知变化规律.



5 推断型
逻辑推理题是近几年高考的创新题型,由于该题不涉及数据,也没有几何图形,只涉及一些相互关联的条件,故该类问题是考查学生抽象思维的很好载体,逐渐受到命题者的青睐.解决这类问题常用的方法有直接法、假设法、排除法、列表法和枚举法等.

甲:我的成绩比乙高.
乙:丙的成绩比我和甲的都高.
丙:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为( ).
A. 甲、乙、丙 B. 乙、甲、丙
C. 丙、乙、甲 D. 甲、丙、乙

甲:甲>乙;乙:丙>乙且丙>甲;丙:丙>乙.
因为只有一个人预测正确,所以分析三个人的预测,可知:乙、丙的预测不正确.如果乙预测正确,则丙预测正确,不符合题意.如果丙预测正确,假设甲、乙预测不正确,则有丙>乙,乙>甲,因为乙预测不正确,而丙>乙正确,所以只有丙>甲不正确,则甲>丙,这与丙>乙,乙>甲矛盾,不符合题意.因为只有甲预测正确,乙、丙预测不正确,所以甲>乙,乙>丙.故选A.

6 信息型
近年来的高考题中,涌现出一种新型试题——新信息型问题,主要考查学生阅读、分析、归纳、内化等综合能力,同时在解题过程中又可应用许多新方法、新观念,从而增强学生创新意识.

A. 18个 B. 16个 C. 14个 D. 12个

根据题意可得,必有a1=0,a8=1,而其余的各项a2,a3,…,a7中有3个0和3个1,并且满足对任意k≤8,a1,a2,…,a8中0的个数不少于1的个数.可以一一列举出不同的“规范01数列”,除第1项和第8项外,中间6项的排列如下:000111,001011, 001101, 001110, 010011, 010101, 010110, 011001, 011010, 100011, 100101, 100110, 101001, 101010,共14个(列举时,可用列表的方式,如图1).
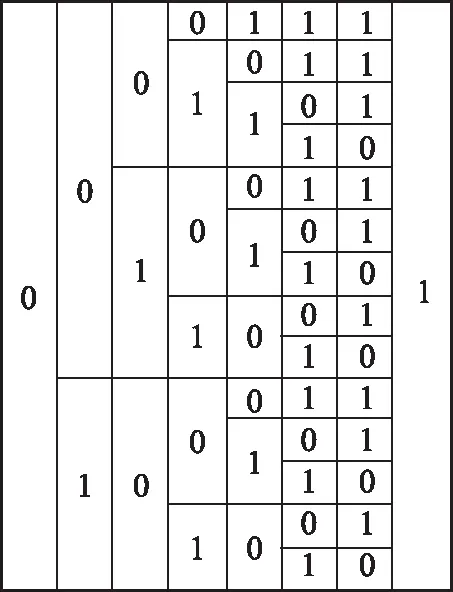
图1
方法2分类计数法.
根据题意可得该“规范01数列”共有8项,其中a1=0,a8=1,则不同的“规范01数列”的前4项按照0的个数进行分类讨论.若前4项全为0,则后4项一定全为1,这样的“规范01数列”只有1个;若前4项有3个0,则前4项的排列有3种,后4项的排列也有3种,这样的“规范01数列”有3×3=9个;若前4项有2个0,则前4项的排列有2种,后4项的排列也有2种,这样的“规范01数列”有2×2=4个.故不同的“规范01数列”共有14种.


