基于非中心分布三个结论的证明

钟韵宁

(广西师范大学数学与统计学院，广西桂林 541000)

0 引言

正态分布是自然界中最常见的一种分布，在正态样本下去构造统计量得到各种统计推断是很有意义的.同时，非中心分布族是常用分布族，在多元分析理论与应用研究中得到广泛重视，很多学者作出了重要研究，例如推导了非中心分布和双非中心分布诸统计量的概率分布密度函数公式[1]，借助超几何函数得到非中心卡方分布的特征函数和非中心F分布的高阶矩[2]，推导广义非中心卡方分布的精确表达式[3].本文基于非中心分布的三个重要结论给出了详细的证明过程.

引理1[4](非中心Gamma分布的可加性)：若X1～Ga(α1,λ,γ1)，X2～Ga(α2,λ,γ2)，且X1和X2相互独立，则X1+X2～Ga(α1+α2,λ,γ1+γ2).

1 结论1

证明：

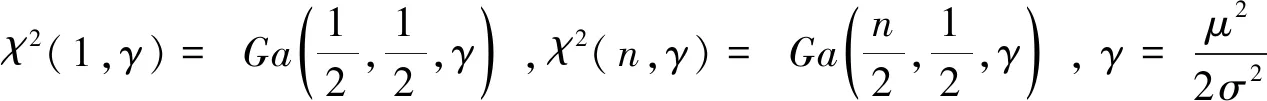
FY(y)=Pr(Yy)

等式两边同时求导，得到的密度函数为

则

由引理1的非中心Gamma分布的可加性，且X1，X2，……，Xn相互独立，所以有

得证.

引理2[4]：设X1，X2，……，Xn是来自N(0,σ2)的一个样本，则

2 结论2

设X1，X2，……，Xn1是来自N(μ,σ2)的一个样本，Y1，Y2，……，Yn2是来自N(0,σ2)的一个样本，且Xi与Yj相互独立，则

证明：

则对(U,V)的联合密度函数关于V积分得到U的密度函数为

所以

3 结论3

设X0～N(μ,σ2)，X1，X2，……，Xn是来自N(0,σ2)的一个样本，且X0与Xi相互独立，则

证明：由X0～N(μ,σ2)，有X0/σ～N(μ/σ,1)，记X=X0/σ，且

则

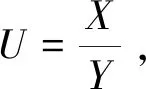
由

则二重积分

其中

所以

所以U的密度函数与t(n,γ)，γ=μ/σ的密度函数相同，得证.

4 结束语

本文中的三个结论对数理统计的基础学习很重要，通过对三个结论的证明过程详细推导，对理解这三个结论和对以后构造统计量得到其他分布有一定的借鉴意义.