关于数列不等式放缩技巧的解析探讨

韩 俊

(江苏省溧阳中学 213357)

一、利用不等式性质，递推巧放缩

求解不等式问题最为基础的方式是结合不等式的性质来逐步推理，对于融合了数列的不等式复合问题同样有效，也更为实用.即首先结合题干信息构建基础不等式，然后分析基础不等式与目标不等关系之间的结构特点，最后结合不等式的相关性质适当放缩，逐步向求证结论推理靠拢，从而完成求解.

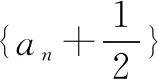
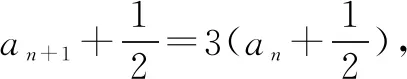
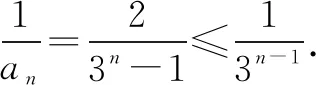
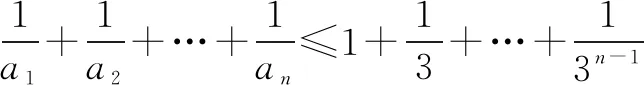
二、调用常见公式，裂项巧放缩

裂项放缩是使用放缩法解题的常用技巧，即通过裂项的方式来达到放缩求解的目的.考虑到数式的结构较为复杂，因此在实际解题时一般需要调用常见不等式，利用公式模型来提高解题效率.

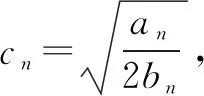
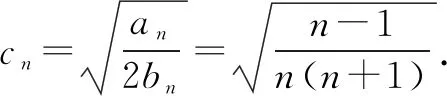
三、调用函数性质，求导巧放缩

数列不等式问题的难点在于将数列和不等式知识有效地融合在一起，从而使问题兼具规律性和推理性.我们知道使用函数的性质可以求解一些最值问题，考虑到不等式与最值之间的关联性，在放缩法解题时也可以调用函数的性质，通过求导的方式来放缩解题.

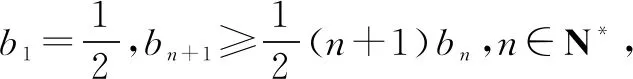
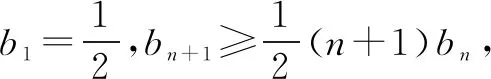
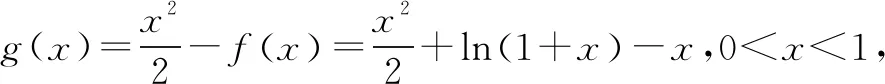
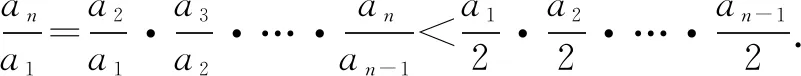
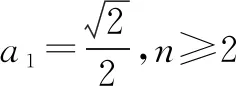
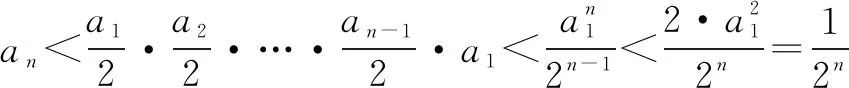
结合①和②式，可得bn>an·n!，证毕.

总之，数列不等式具有数列和不等式的双重特性，因此掌握数列和不等式的基本性质是解题的基础.利用放缩法求解数列不等式问题的技巧有很多，上述所探讨的利用不等式性质、调用不等公式和函数性质只是其中常用的三种，实际上就是利用数学对应知识的整体性、有界性和递推性来进行缩放.而在实际解题时需要我们充分利用问题条件，善于分析不等式的结构，灵活选用放缩技巧来转化突破.