例谈高考数学估算型试题解题策略

纪定春 蒋红珠 周思波

(1.四川师范大学数学科学学院 610068；2.广东华南师范大学数学科学学院 510631)

一、估算的教育价值

精算与估算相结合是数学教学的重要原则.估算和精算系统之间有着密切的联系，相互支撑，共同发展.纵观我国数学教育(或教学)史，数学教育(或教学)一直以来注重学生的精算能力的培养，忽略估算素养的形成.估算是指个体在利用一些估算策略的基础上，通过观察、比较、判断、推理等认知过程，获得一种概略化结果.可见，估算是一种创造性的数学思维活动，需要学生根据已有的知识基础，通过观察、比较、判断、推理等认知过程创造性地进行“粗略”计算而得出概略化结果的方法.估算不同于精算，精算是需要一定的数学符号，遵循算法和算理，按照一定的步骤得出较为精准的结果，即定量分析；而估算只需要进行定性分析，得出一个“大概”或者是“粗略”的结果.高考数学估算型试题，可以有效地激活学生的数学创造性思维，对培养学生数学创新意识和数学创新能力具有重要的作用.本文拟以审美估算、极限估算、特殊值估算、常识性估算等策略，对近年高考数学估算型试题进行了分析与点评.

二、高考数学试题的常见估算策略

1.审美估算策略

教育部2017年版普通高中课程标准指出，要让学生认识数学的科学价值、应用价值、文化价值和审美价值.可见，数学教育不仅要教会学生数学审美，更要让学生学会欣赏数学美、创造数学美.正如苏霍姆林斯基所讲“没有审美教育，就没有任何教育”.学会审美不仅可以陶冶情操，而且能够改善思维品质.数学中的美包括简单美、对称美、奇异美、和谐美等.审美估算策略，就是用数学美的眼光来欣赏、判断、解决数学问题的一种估算方法.审美估算型试题是近年高考数学的热点题型，值得关注.

例1(2017全国理科卷Ⅲ第11题)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点，则a=( ).

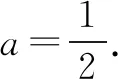
点评该试题蕴含丰富的数学美，如对称美和简单美，函数的图象是高度对称的，并且极值点恰好就在对称轴处取得.可见，该题的设计含有“数学美”的“美育”意图.利用二次函数的对称性和指数函数的对称性来估算，简单有高效.可见，用欣赏数学美的眼光来解决高考数学试题，亦是一种有效的解题策略，若用导数工具来研究函数f(x)的性质，则显得相对繁琐.

2.极限估算策略

极限思想作为一种重要的数学思想，是有限到无限的桥梁，贯穿于整个高等数学.高中数学也不乏极限思想的渗透，如函数单调性定义中的“任意性”，用于描述函数切线变化情况(割线的极限)的导函数，用有限步骤来证明无限命题成立的数学归纳法等，无不涉及极限(无限)情形.极限估算策略是一种用极限的眼光和极限的思维来观测、估算动态最值或极值的一种策略的.极限思想具有丰富的内涵，对处理无穷问题提供了有力的工具，同时对进一步学习高等数学具有重要的价值和深刻的意义.

例2(2017全国理科卷Ⅰ第10题)已知F为抛物线C:y2=4x的焦点，过F作两条相互垂直的直线l1，l2，直线l1与C相交于A，B两点，直线l2与C相交于D，E两点，则|AB|+|DE|的小值为( ).

A.16 B.14 C.12 D.10

思路1估算法

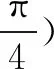
思路2极坐标法

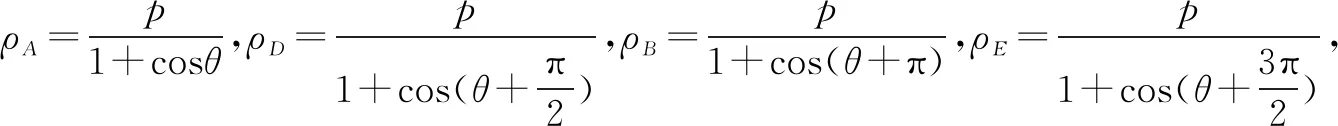
点评该试题若用直接设点求最值的方法可以做出来，但是过程繁琐，运算量大且容易出现过程性失误.利用两条直线的互相垂直及所求，将两条直线“运动”(极限过程)起来，定性分析两条线段相加后所得值的一种“趋势”，判定不可能的情况，进而作出合理的猜测和估算(估计)，这样可以有效地提高问题解决的速率和准确率.对比思路1和思路2，可以发现，虽然用极坐标更简捷地解决了该问题，但是思维量仍然不小.可见，利用极限估算策略极大地降低了思维量，这正体现了高考数学试题“多想少算”的命题原则.

3.特殊值估算策略

特殊值估算策略，就是一种在充分地挖掘题干已知条件基础上，利用题的特殊性质、特殊点、特殊值等进行推理、判断的数学思维方法与思维活动.特殊值不仅限于有限的特殊值，可以是“无穷”的特殊值，如正无穷、负无穷.近年，高考数学选择题就出现了很多关于图象判断的试题，这类试题在平时的检测中较为少见，对这类题目缺乏练习和经验的积累，考生在考场遇到此类试题有些不知所措，因此要关注高考数学中的特殊值估算法.

例3(2016全国理科卷Ⅱ第7题)函数y=2x2-e|x|在[-2,2]的图象大致为( ).

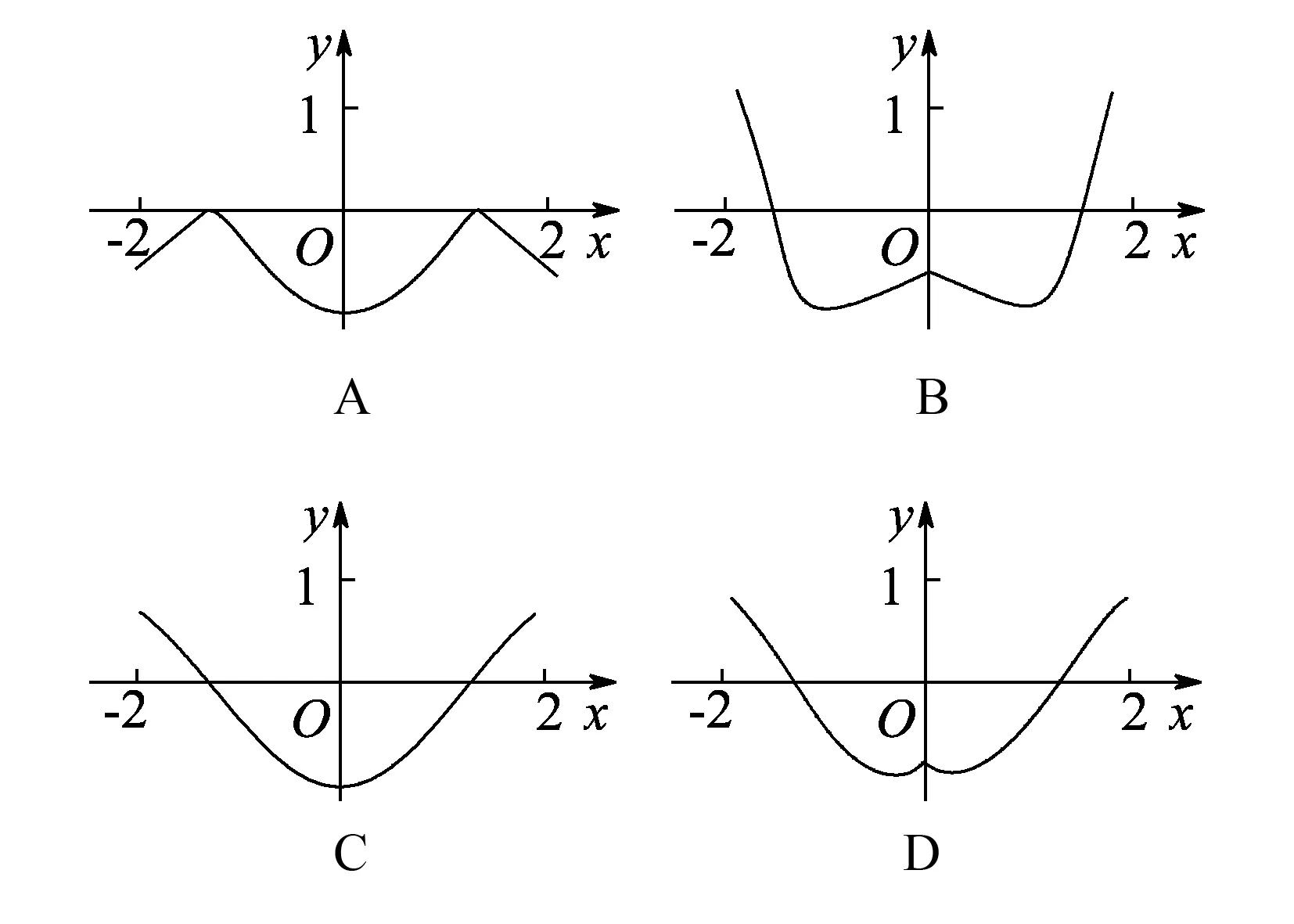
解析由题可知，这是关于闭区间上连续函数的图象性质判定问题，可以考虑使用特殊值估算策略.注意到特殊点“右端点”，当x=2，估算可得y≈0.5，观察上述四个选项，可以先排除选项A和B，选项A明显不对.选项B的错误不够明显，仔细观察会发现，当x=2时，函数值y明显大于1，故排除选项B.对于选项C和D，由于对称性，可以只考虑y轴右边部分.观察发现，两个图象的唯一区别就是两个选项的图象在x∈(0,2)上有无极值点，考虑用导数来研究函数极值存在的情况.对x求导，可得y′=4x-ex，取特殊值点x=0以及x=2.可得，当x=0时，y′=-1<0，当x=2时，y′>0.故导函数y′=4x-ex在区间x∈(0,2)上有零点，故原函数存在极值点，所以排除选项C，故选D.

点评该试题主要考查函数的局部性质和局部的图象，具有较强的综合性.根据当时的考试情况，因为没有注意细节和取特殊值进行估算，很多学生最后无法判断选项B和选项D.选项B的判断，充分地体现了特殊值估算策略的优势.对于选项C和D的判断，充分地利用了导函数在x=0和x=2处这两个特殊值(取x=0及x=1同样可行).

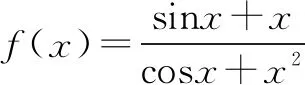
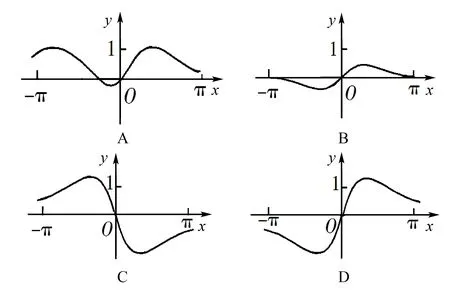
解析显然，可知函数f(x)的分子为奇函数，分母为偶函数，经过复合之后，可得函数f(x)为奇函数，故可以直接排除选项A.注意到这是判断闭区间上函数的图象，故可以考虑估算特殊值点x=π处f(x)的值，代入可得f(π)>0，可得选项D正确，故选D.

点评该题主要考查函数的性质：奇偶性.显然这个函数的奇偶性隐藏得比较“深”，一般不容易察觉，从考试的情况反映出，高考中有很多考生都错选成A，这表明很多考生并没有判断出函数的奇偶性.如果借助导函数来研究函数的性质，将是困难和繁琐的，此处用取特殊值策略对排除无关选项起到了关键性的作用，更好地正确解决了该问题.

4.常识估算策略

对数学的知识的认识水平，可以大致可以分为常识、理解、记忆、应用、评价和创造等，评价和创造属于对数学的高级认知能力.常识性知识是在生活的过程逐渐积累形成的感性经验，是一种不需要教的知识(不教而会的知识)，符合人们对事物认知的知识.常识估算策略就是采用数学常识、生活常识及其它常识性知识来解决数学问题的一种方式.

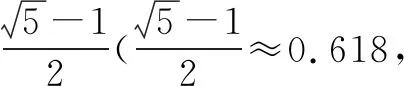
A.165cm B.175cm C.185cm D.190cm

解析该题主要考查学生的阅读理解能力、生活常识、估算能力等.最简单的方法是“猜”，就是根据常识去“猜测”、去合理地“估算”(这里的“估算”不是统计中所说的“估值”)，然后再去检验.通过常识猜测，可直接排除选项C和D，这是因为古代人身高普遍比现代人身高低，断臂维纳斯作为古希腊“美”的象征，显然不符合当时的审美要求.对于选项A，维纳斯是欧洲人(希腊人)，一般要比中国人高，故选择B.可见猜测就是一种从“审美”和“常识”的视角出发，来推测正确答案的方式.若出于放心的选择“猜测”，可进行验算(粗略的估算).除了从常识的视角来解答外，还可采用估算的方式，将黄金分割数0.618近似的看成0.62或0.6来计算(估算)，这样最大限度地可降低运算量，提高准确性，同时可在估算过程中培养学生的创造性思维、数据处理能力及数学直觉思维等.选B.

点评试题以古希腊“断臂维纳斯”为背景，其设计意图内涵丰富，第一揭示数学中美的标准就是黄金分割；第二数学是判断(检验)美的一种标准；第三具有“文化育人”的价值，引导数学教学要重视“数学美”的渗透，进而重视数学文化的教育.高考后发现，本题是让很多考生头痛的“难题”，第一是很多考生误认为是计算“断臂维纳斯”的身高；第二是不知道如何列式计算；第三是感到计算量太大，不知该题的本质主要是考查估算能力；第四是题中“某人”身高是不确定的，属于“结论开放性问题”，考生对这种开放性问题没有在教学和训练范围之内，缺乏解题经验和思路.

高考数学估算型试题作为一种重要的试题类型，在高考数学中占据重要的地位，估算型试题对于培养学生灵活处理问题的能力和激活创造性思维具有重大的教育意义.我国数学教学历来注重精算能力的培养，也注重精算能力的考查，这是必要的也是合理的，但同时要关注学生估算能力的发展，要做到数学思维“两条腿”走路，即精算和估算协调发展.

数学教学是数学思维的教学.估算是通过观察、比较、判断、推理等认知活动过程共同协调完成的，获得的是一种粗略化的思维结果，对降低学生的思维负担具有重大价值，这样可以留出更多的时间来供学生思考更有价值和意义的问题.心理学研究表明，兴趣来自于对成功的体验.因此，在数学教学过程中，要善于抓住机会，通过估算教学来展现估算的魅力和神奇，让学生在体验成功估算的过程中激发学生对数学的学习兴趣，启迪学生的数学思维，并在估算与精算的相互协调中，促进学生对数学知识理解，对数学本质的理解及数学思维的形成.