轮辐式航线网络下的超售策略研究①

王丹丹 秦雪婷 沈佳 岳晶晶 张淳熙 张蒙明月

(中国民航大学理学院 天津 300300)

轮辐式航线网络是指一个航空公司将其所有的航线以枢纽机场为起点，各目的地机场及其他枢纽机场为终点进行布局的航线网。过去的收益管理一般是在单航段情况下进行的，但是单航段的收益最大，并不能确定多航段航线收益最大化。基本的存量控制模型(EMSR）方法是基于航段的收益最优化方法，张宇宁，牟德一，赵宇洋，姚雨沁，高忠文，何楚君[1]所做的基本假设与本文接近，确定航班各舱位座位数量，使航线而非航段收益最大化，建立随机规划模型，并使用蒙特卡罗方法对现实情况进行仿真,再利用冒泡搜索算法,搜索出模拟情况中使超售成本最低的超售数量，但是未考虑舱位嵌套控制。其模型假设及航线整体思想对本文具有一定的参考意义。高金敏，乐美龙[2]研究轮辐式航线舱位控制，假设不同舱位需求独立且服从正态分布，不同票价的旅客订座顺序不同，且不考虑no-show情况，此项目在提高航班的收益上具有一定创新性和有效性。

本文讨论最大收益下的最佳超售数，舱位控制涉及较少，均看作同等舱位。收益管理分为四个主要部分：需求预测，订价，舱位控制和超售。机票超售的原因是旅客订票后并未购买或购票后在不通知航空公司的情况下放弃行程，从而造成航班座位虚耗。为了满足更多旅客的出行需要和避免航空公司座位的浪费，航空公司会在部分容易出现座位虚耗的航班上，进行适当的超售。但是另一方面，若出现超售数目过多，则会造成旅客被拒载的情况，这无疑为航司还有旅客增加经济上以及时间上的负担。因此，本文一个关键点就在模拟旅客退票情况，控制超售数目，寻找收益最大化的超售数。

1 轮辐式航线网络下的超售策略研究问题描述

轮辐式航线网络下的超售策略研究旨在利用运筹学、统计学相关知识及MATLAB软件解决民航企业中管理问题——收益管理。在以往已经成熟的单航段超售模型基础上，建立网络环境下超售的随机规划模型，并结合实际研究模型的应用案例，对模型进行解释与评估。

轮辐式航线网络结构与单航线结构相比较，其特点便是存在中转联程航班，所以其中每个航班不仅承载着直达旅客，并且同时承载着相应的联程旅客。网络环境下，超售策略的实施需要对每段航程与联程航班no-show数进行预测。航空公司根据历史数据和现有的市场分析，对单段航程和联程航班的no-show数进行预测，并充分利用预测结果，确定每段航程与联程的座位超售数。对出现空位和拒载的情形采用互补方式，以尽可能减少出现座位虚耗与拒载情况，故而实现收益的最大化。问题研究将会分别介绍单航程与联程航班的超售情况，通过对比收益大小说明轮辐式航线网络下的超售策略的优越性。

2 单航节超售模型

2.1 模型建立

假设飞机容量为n，超售数量为r，已订票而未按时登机的乘客数为q（q是一个变量），假设每位订票乘客不按时登机的概率即no-show率为b，他们是否按时登机相互独立，假设每张机票价格为p，s表示因为超售导致飞机满员而发生拒载而对乘客的补偿为（包含退还机票款）。

根据已经购票而未按时登机的旅客数量q的多少，航空公司的收益有两种情况：

当q≤r（n+r-q≥n）时，即按时登机的旅客数量大于航班座位数，发生拒载情况，则只有n名旅客可以登机，机票收入为p*n，剩下r-q位旅客因无法登机而得到的补偿为s(r-q)，于是航班收益为p*n-s*(r-q);

当q＞r（n+r-q＜n）时，即按时登机的旅客数量小于或等于航班座位数，则他们均可登机，航班的收益为p*(n+r-q);

综上，记该航班的收益为s(q,r)，则

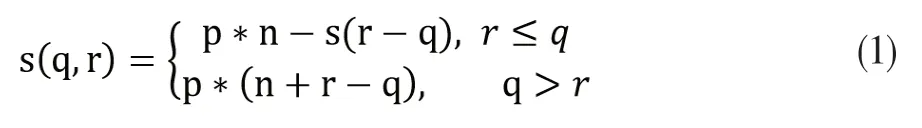
对于已订票的n+r位旅客中恰有q位不按时登机的概率记作f(q),q=0,1,…,n+r，则航班的收益的期望值记作E(r)

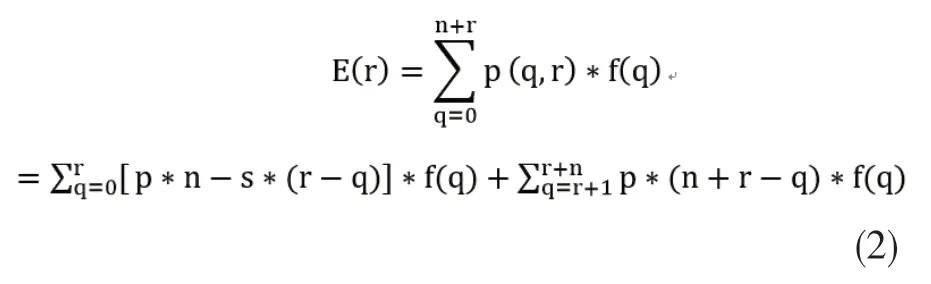
其中，每位乘客的no-show率为b，且他们是否按时登机服从二项分布，则变量q服从二项分布

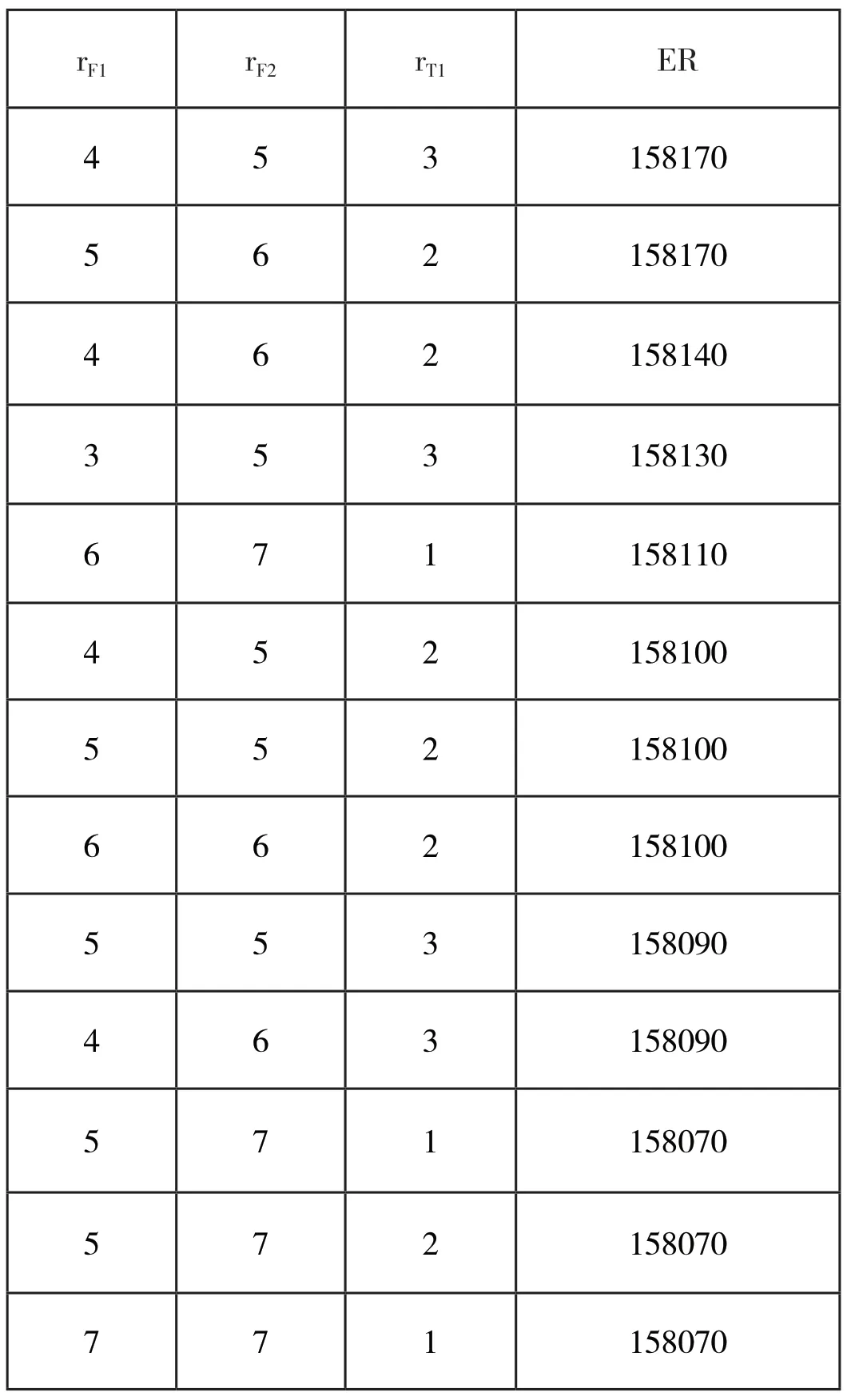
表1 穷举法下超售数组合及其对应收益

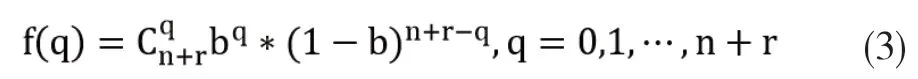
运用离散需求下的报童销售模型，可以得到最优的r满足如下不等式

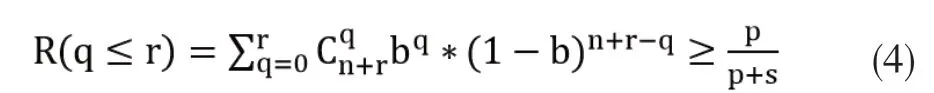
基于上述不等式，利用MATLAB软件逆二项分布求解出最佳超售数r的取值。

2.2 算例分析

假设航班从A飞往B，各项参数如下：

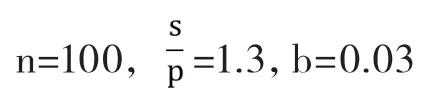
得出最佳超售数为4。即在座位数是100，no-show率为3%的情况下，如果发生拒载，补偿给乘客的金额为机票价格的1.3倍。此时，最佳的超售数为4。

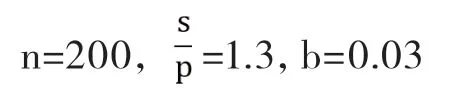
得出最佳超售数为8。即在座位数是200，no-show率为3%的情况下，如果发生拒载，补偿给乘客的金额为机票价格的1.3倍。此时，最佳的超售数为8。

3 轮辐式航线网络下（多航节）的超售模型

3.1 模型建立

如图1，本模型的建立是基于如下假设：（1）每位旅客按时登机的概率服从二项分布，且是否按时登机的行为相互独立；（2）没有按时登机的人数即no-show数是一随机变量；（3）舱位不分等级，均按同等级舱位处理；（4）航班飞行成本和联程航班飞行成本相同；（5）航班于联程航班对于拒载旅客的补偿价格相同；（6）放出的机票全部卖出，对于no-show的旅客实施退票处理。

模型中用到的符号定义如下：

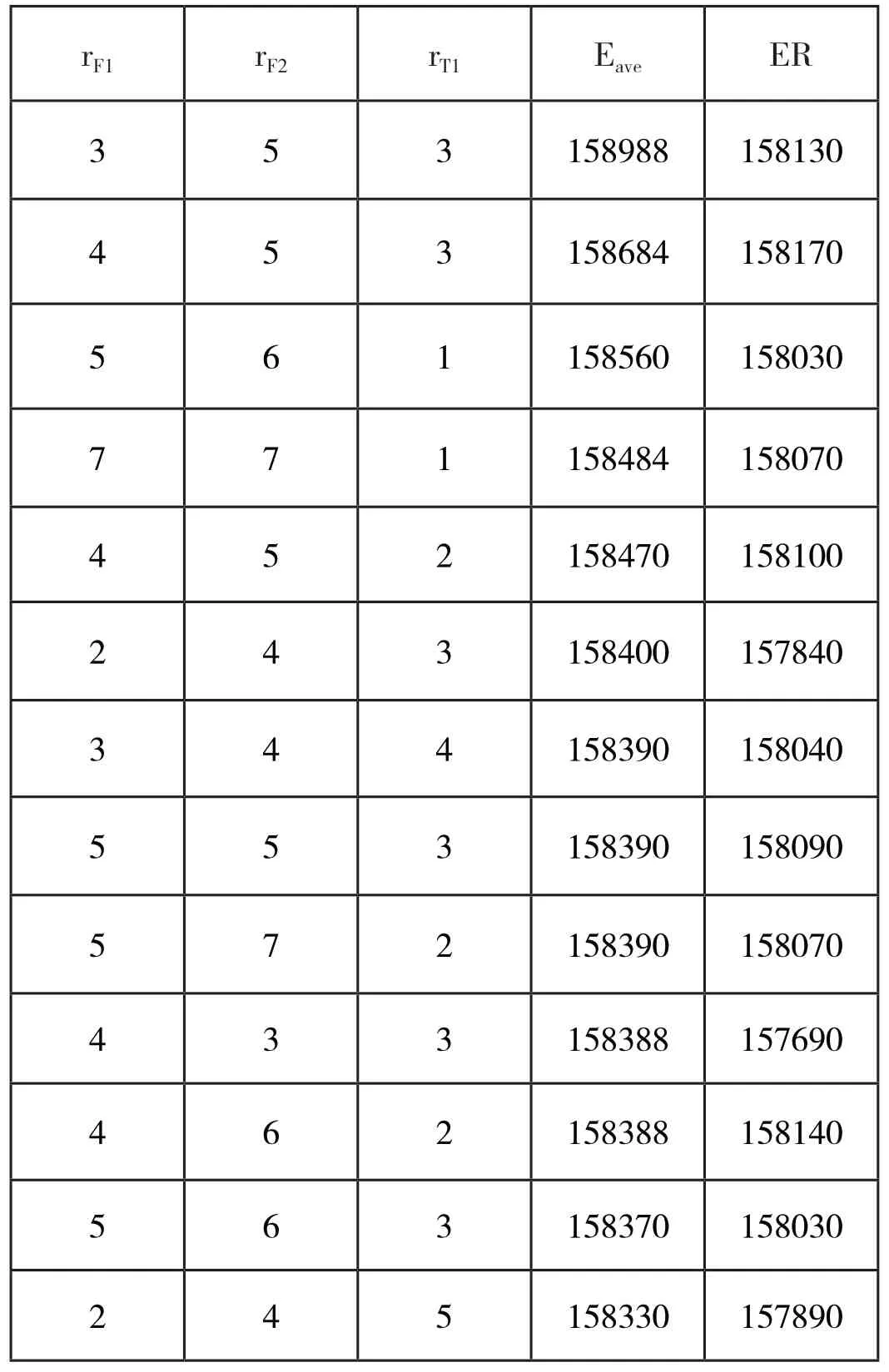
表2 仿真模拟法下超售数组合及其收益

集合F为航班集合；T为联程航班集合

下标f为航班下标，f∈F，f=1,2,3,……,i；t为联程航班下标，t∈T，t=1,2,3,……,j；

参数pFf、pTt分别为航班和联程航班票价；nFf、nTt为座位数；rFf、rTt为座位超售数；qFf、qTt为no-show数；s为拒载旅客的补偿价格；α为飞行成本；EFf、ETt为期望收益。

航班F1、F2与联程航班T1预先分配座位分别为nF1,nF2,nT1。

考虑AB航段，若航班F1在单航线模型下出现拒载情况，而联程航班T1在单航线模型下出现空座情况时，则将联程航班T1的空座分配给航班F1；反之，亦然。考虑BC航段，航班F1的旅客全部离开，保持到达B地时的联程航班T1的旅客座位数不变，此时问题可转化为单航线模型进行讨论。

下面分四种情形进行讨论。

情形Ⅰ. AB航段中航班F1与联程航班T1均存在空座情况(rF1＜qF1,rT1＜qT1)，讨论BC航段。

若航班F2在单航线模型下出现拒载情况，且拒载人数大于联程航班T1的空座数，则BC航段出现实际拒载情况，即rF2＞qF2且(rF2-qF2)＞(qT1-rT1)时，总收益为

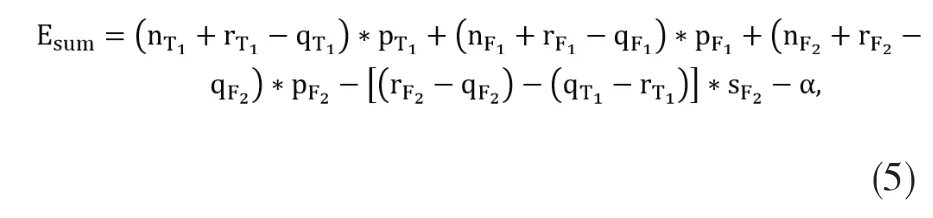
反之，若各个航段均不出现实际拒载情况。此时收益如下：

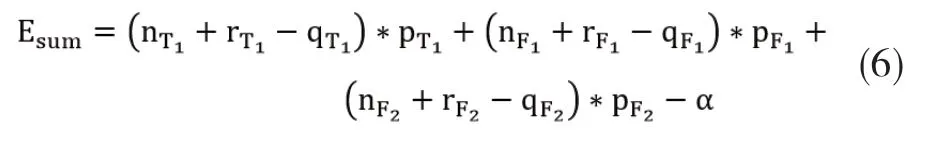
情形Ⅱ. AB航段中航班F1在单航线模型下出现拒载情况而联程航班T1存在空座情况(rF1＞qF1,rT1＜qT1)，则航班F1与联程航班T1的收益如下：

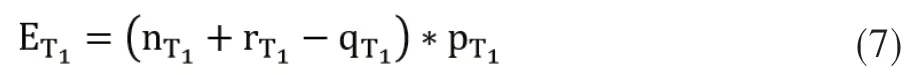
当(rF1-qF1＞(qT1-rT1)时，即F1航班拒载人数大于T1航班空座人数时，

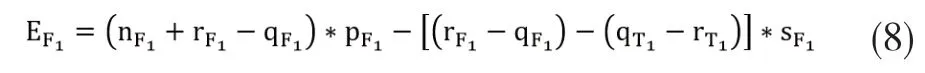
当(rF1-qF1)≤(qT1-rT1)时，即F1航班拒载人数小于等于T1航班空座人数时，

接下来我们讨论BC航段的情况，到达B地若联程航班T1还有空座，则空座数为(qT1-rT1)-(rF1-qF1)。若航班F2在单航线模型下出现拒载情况，且拒载人数大于联程航班T1的空座数，即当(rF2-qF2)＞(qT1-rT1)-(rF1-qF1)时，航班F2收益为；

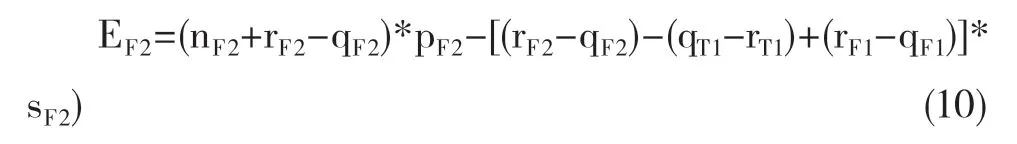
反之，当航班F2没有出现拒载情况，或者出现拒载情况，但拒载人数小于或等于航班T1空座人数时，即(rF2-qF2)≤(qT1-rT1)-(rF1-qF1)，此时航班F2收益如下：

总收益如下：

情形Ⅲ.AB航段中联程航班T1在单航线模型下出现拒载情况而航班F1存在空座情况(rF1＜qF1,rT1＞qT1)，则航班F1与联程航班T1的收益如下：

当(rT1-qT1)＞(qF1-rF1)时，即T1航班拒载人数大于F1航班空座人数时，

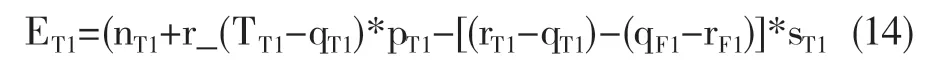
当(rT1-qT1)≤(qF1-rF1)时，即T1航班拒载人数小于等于F1航班空座人数时，

到达B地时，在原单航线模型下联程航班T1仍存在拒载情况，引入符号γ表示此时联程航班T1超出预先分配座位数nT1的部分(γ=min{(rT1-qT1),(qF1-rF1)})，则航班F2收益如下：

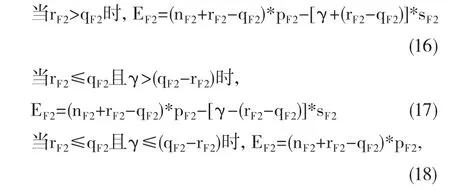
总收益为：

情形Ⅳ.AB航段中航班F1与联程航班T1均存在拒载情况(rF1＞qF1,rT1＞qT1),则航班F1与联程航班T1的收益如下：

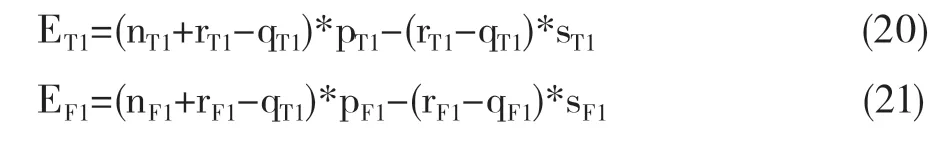
到达B地时联程航班T1的旅客数等于预先分配的座位数，只需考虑航班F2的情况。则航班F2收益如下：

当rF2＞qF2时，即超售数目大于没来旅客的数目情况下，

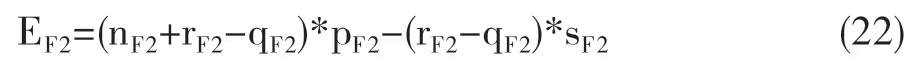
当rF2＞qF2时，即超售数目小于或等于没来旅客的数目情况下，

总收益如下：

3.2 算例分析

通过计算，在单航线模型（4）的结构下，得出座位数为200时的最佳超售数为8，于是我们认为，在座位数为100的情况下，确定超售数目rF1,rF2,rT1的取值范围在0～8之间，即0≤rF1,rF2,rT1≤8。

为寻找固定座位数组合下使收益达到最大的最佳超售数组合，使用如下方法：

方法一：运用穷举法，对所有超售数组合的期望收益计算其精确值，最大的期望收益精确值所对应的超售数组合即为最佳超售数组合。

期望收益精确值的计算公式为：

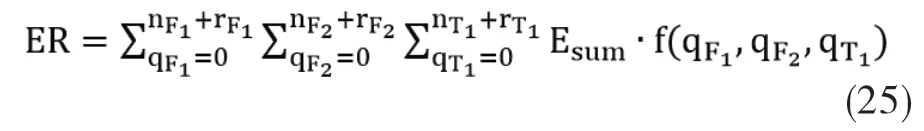
其中

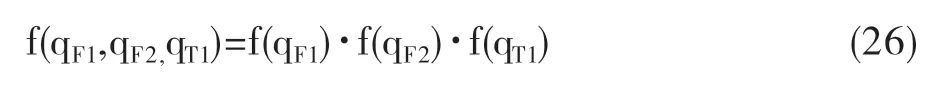
因超售数目服从二项分布，于是我们有qj～B(nj+rj，pj)，其中j表示航班。

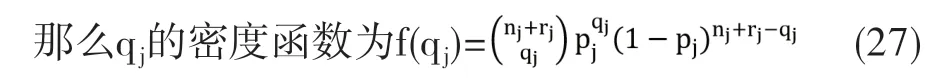
我们假定各个航段的旅客没来的概率均为0.03，通过上述模型运用MATLAB软件计算得到如表1。

此种方法下得到的最佳超售数组合有两组，分别为：

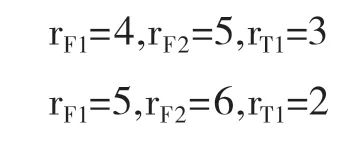
由表1可以看出，当航班F1、航班F2和联程航班T1的超售组合分别为（4,5,3），或（5,6,2）时，航空公司的期望收益精确值达到最大。

方法二：首先，运用仿真模拟的方法，在每种不同的超售数组合下，随机生成30组no-show数组合，计算其对应的收益后取均值得到平均收益Eave；其次，选取Eave最大的几组超售数组合，并计算其对应的期望收益精确值ER；最后，最大的期望收益精确值ER所对应的超售数组合即为最佳超售数组合。

仿真模拟的得到的特定超售组合下的平均收益Eave虽存在较大随机性，但是根据期望收益精确值ER较大的超售数组合在多次模拟中更倾向于得到较大的Eave，认为此种仿真模拟方法是可取的。此外，方法二兼顾了仿真模拟与理论期望，且在运行速度方面明显优于方法一。

结果如表2所示。

此种方法下得到的最佳超售数组合为：

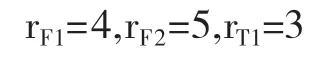
即在航班座位数为100的情况下，当航班F1、航班F1和联程航班T1的超售数分别为4、5、3时，仿真模拟得到的平均收益是较大的，且在仿真模拟得到的平均收益值降序排列的几组超售数组合中，此种策略将使航空公司的期望收益精确值也达到最大。

4 轮辐式航线网络下的超售策略研究结论

本文主要研究轮辐式航线网络下的超售策略，通过仿真模拟的方法求出联程航班中每个航班的超售数，并分析4种情形下的联程航班的最终收益。在与同段单航线航班的收益进行对比后，说明轮辐式航线网络下超售策略的优越性。其结论通过如下示例说明：

在模型假设下，F1、F2、T1，三个航班分别有100个座位，根据上述结论，

各航段超售数分别为rF1=4,rF2=4,rT1=4。F1、F2、T1航段的机票价格分别为800元、1200元、2000元，飞行总成本为240000元。

首先，运用MATLAB仿真模拟旅客是否来到的情况，在每个航段下，随机生成30组no-show数组合，计算其对应的收益后取均值得到平均收益，并求和减去飞行成本，得到单航线下模型下航班的总收益E，此时由模型（4）得到100座下的最佳超售数为4，所对应的航班超售组合为（4,4,4），此时各个航班及总收益值结果如下：

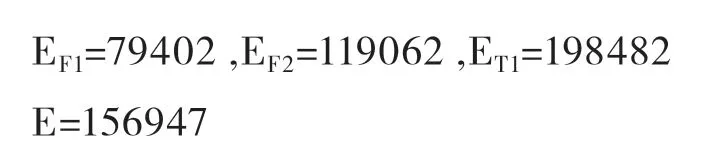
接下来计算在固定超售数组合（4,4,4）情况下，利用多航节模型对旅客的座位进行调整后的航班收益。即将某一航班拒载的旅客调换到另一具有空座情况的航班上，也就是对拒载的旅客进行座位分配，再计算总收益。此时运用多航节下的模型（25）得到新的收益值，记为E1，计算结果为E1=157930。可以看出该收益值与原来没有对旅客进行座位分配得到的收益值相比，有了明显的提高。

随后，进一步对航线网络各航段的超售数进行调整，同时对旅客进行座位分配，此时再计算航班收益。在模型（25）的基础上，利用MATLAB软件模拟计算各个超售组合下的收益值，得出使收益最大的超售组合和最高收益值E2，结果如表2所示。从表中可以看出，当超售组合为（4,5,3）时，对应最佳收益值为E2=158170，此结果和模型（4）得出的收益值相比，有了更显著的提高。

由上述示例可以看出，与单航线下模型下航班的总收益相比，在固定原有超售数，并对拒载旅客进行座位分配的情况下，收益提高了0.63%；进一步，通过对超售数进行调整后，收益提高了0.78%。

综上所述，通过比较单航线模型和联程航线模型下计算的航班收益，可以得出轮辐式航线网络下的超售策略可以有效提高航空公司的收益，证明了轮辐式航线网络下的超售策略相对于单航线情况下的优越性，同时凸显其研究意义。

5 结语

航线网络是指某一地域内的航线按一定方式连接而成的构造系统，其由机场、航线和飞机等要素构成，其中机场和航线构成了航空运输的空间分布，决定了航空运输地面和空中保障能力，而飞机则通过航线由一个机场飞到另一个机场已实现旅客、货物、行李和邮件的空中位移。航线网络是航空公司航班计划和机组安排等运行计划的先决条件，对航空公司的运行效率和客户的服务质量有着重要的影响作用，是航司生存和发展的基础。

航线网络分为点对点、城市对、中枢轮辐式等几种网络结构，其中轮辐式航线网络具有规模经济性、范围经济性、信息经济性等特点，然而它却存在有更长的飞行距离、更多的起降、地面操作成本以及更大的飞机利用率挑战等劣势。对于旅客来说，航班频次的增多无疑方便了旅客的出行，但同时，枢纽航线网络的延误、拥挤会严重影响商务旅客的出行时间，从而使得其对航司的好感度降低。

因此，虽然超售在一定程度上的确能够减少航班收入损失，提高公司收益，但对于一家航司来讲，其更要注重的是航线的排布，以及自家航司的产品、服务质量。只有根据自家航司的特点，创造自有特色的产品和服务，才能为公司带来更大的收益。