多欧拉域耦合法在平尾鸟撞中的应用
胡文刚,林长亮,王刚,门坤发
航空工业哈尔滨飞机工业集团有限责任公司 飞机设计研究所, 哈尔滨 150066
鸟撞是指飞行器与天空中飞行鸟类相撞造成的飞行事故。目前,对于飞机机头罩、风挡、机翼、尾翼前缘、发动机叶片等易遭受鸟撞的结构,国内外都开展了大量的试验和分析研究。
Reza和Saeed[1-2]讨论了不同鸟体形状对冲击的影响,通过数值计算与试验对比,确定了仿真的鸟体形状,并采用野鸭的物理模型,研究了真空、空气和不同撞击方向对鸟撞响应的影响。McCallum等[3-4]用天鹅物理尺寸建立鸟体,通过研究发现,含头、长颈的鸟体模型能正确预测冲击载荷及靶体破坏,且计算结果冲击时程更长,冲击力极值更大。Lakshmi[5]建立了真实鸟体模型,对不同部位取不同密度,通过研究发现,分析小鸟体鸟撞问题时可用传统的简化鸟体躯干模型,但在分析大鸟体鸟撞时鸟体中的其他部位不可忽视。Hedayati等[6-7]建立几何形状更准确精细的鸟体模型,研究真实形状鸟体从各部位对结构冲击的靶体损伤,并将真实形状鸟体计算结果与替代模型计算结果及试验结果进行了对比,结果表明真实鸟体模型计算结果与理论计算值差别较大,与试验值吻合较好。Guida等[8]对设计的3种纤维金属层合板前缘结构进行冲击能量吸收性能测试,对比分析了3种结构的抗鸟击性能;Dar等[9]研究了不同撞速和不同撞击角度下风挡的鸟撞动响应。Liu等[10]采用有限元与光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)结合的方法对某商用飞机平尾前缘进行了鸟击仿真,与试验结果进行了验证,并提出了在前缘结构中引入三角钢筋构件,能够显著提高前缘结构的抗鸟撞性能。Caprioa等[11]研究了垂尾前缘的抗鸟撞性能,讨论了不同材料系统如何满足前缘结构的减重需要和抗鸟击性能,采用经过试验验证的数值程序,分析了几种典型前缘结构的抗鸟撞性能。Yu等[12]提出了一种确定鸟类撞击造成最严重损伤的临界位置的分析方法,利用PAM-CRASH软件,分析了鸟体垂直于机翼前缘的冲击损伤,指出传统的鸟体平行于前缘冲击得到的临界速度不是结构抗鸟撞的最小速度。Xie等[13]采用霍普金森拉杆(SHTB)系统进行了平尾前缘常用的2024-T3和7075-T6铝材不同应变速率下的拉伸试验,建立了反映铝合金应变率硬化效应的约翰逊-库克模型。中国ARJ21垂尾抗鸟撞设计是通过与美国ASC公司合作通过适航审查的。Wilbeck和Barber[14]采用10%孔隙率的明胶,制作2∶1的圆柱体来模拟鸟体,通过大量试验和计算,指出在50~300 m/s的冲击速度下,鸟撞可看作非恒定的流体动力学过程。总结了鸟撞过程主要分为初始撞击、压力衰减、恒定流动和流动结束。Zhang和Fei[15]采用SPH粒子法,对比了经典的半椭圆球形鸟体和真实鸟体对发动机风扇的冲击响应,结果表明鸟体形状和撞击方向对鸟撞结果有很大的影响。
陈贺贺等[16]研究了4种鸟体本构模型对风挡的鸟撞,提出SPH粒子法和自定义本构鸟体的计算精度较高。潘春蛟等[17]对直升机主桨变距拉杆鸟撞进行了数值模拟,提出高速鸟撞造成变距拉杆功能失效的危害较大。朱贝蓓和蔡景[18]采用马尔科夫链蒙特卡洛法,对中国运输机鸟撞冲击能量开展了研究,建立了鸟撞冲击能量的概率分布曲线。陈静和蔡景[19]提出了一种基于SPH粒子的鸟撞修正算法。张海洋等[20]使用PAM-CRASH软件,对发动机吞鸟导致的叶片损伤进行了数值模拟,给出了叶片的主要损伤形式和部位。庞华华和韩全民[21]建立了全尺寸复合材料平尾有限元模型,通过对比试验结果,对模型做出修正。幕琴琴等[22]研究了旋转离心力对鸟撞叶片响应的影响。刘军等[23-24]对鸟体本构模型进行了反演,研究表明鸟体与平板之间存在强烈的耦合效应,中心点最大变形是平板厚度的7.9倍,鸟体撞击速度越高,流体特性越明显。王计真和刘小川[25]提出了一种鸟体本构参数识别方法,并通过鸟撞试验验证了该方法的准确性。
综上,已有的研究大都限于数值计算,鸟体本构以及简单试件或结构的鸟撞试验,分析区域多是鸟体的第一撞击部位。对大型全尺寸结构以及鸟体穿透撞击点后,对其他结构撞击的分析研究较少。本文建立了全尺寸平尾模型,使用多欧拉域耦合的方法,在考虑空气影响的前提下,分析了鸟撞对平尾整体结构的影响和前缘损伤,并与试验结果进行了对比。
1 鸟撞试验
根据CCAR29部第29.631要求,旋翼飞行器在速度等于最大极限速度(VNE)或者最大平飞速度(VH)(取较小者)受到1.0 kg的鸟击后能够继续飞行或者安全着陆。根据要求,试验的鸟弹质量为1.0 kg,撞击速度为90.6 m/s。撞击位置选择在鸟撞击平尾后能够使平尾产生最大弯矩的位置。因此,撞击点选择在平尾最外侧前缘2个小肋之间。平尾通过钢制支撑结构与试验平台连接,试验平台装置及工装见图1和图2。试验设备由发射系统、试验靶架系统、速度测量系统和高速摄像系统组成,见图3。
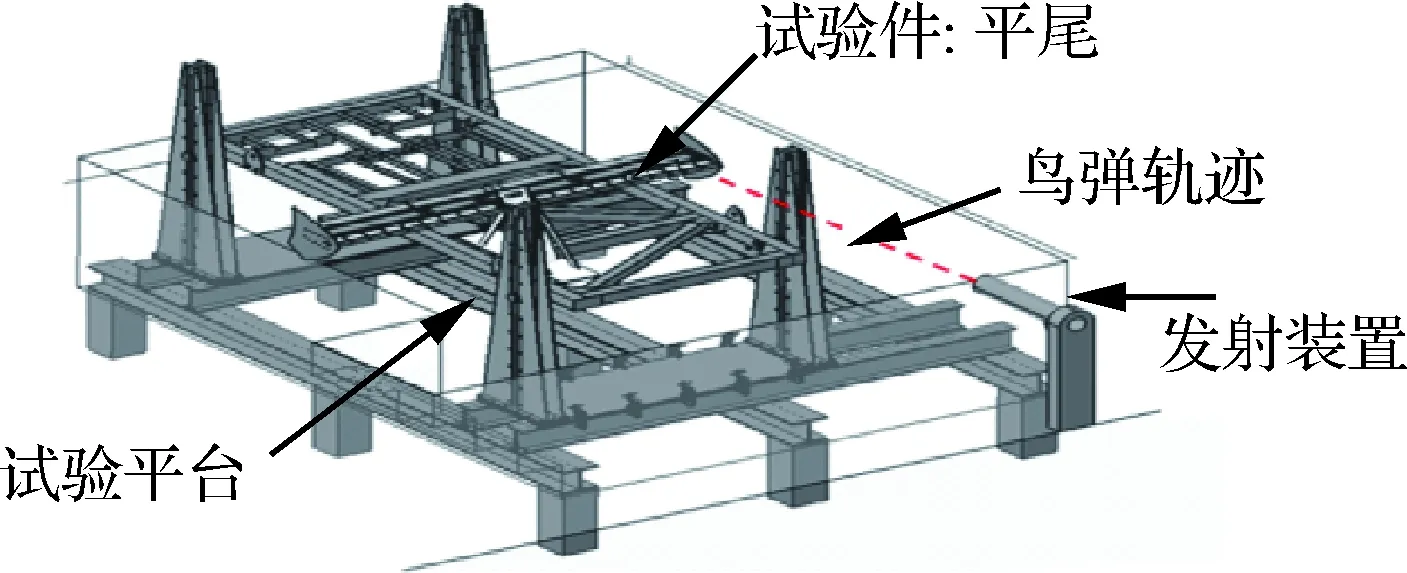
图1 鸟撞试验平台示意图Fig.1 Diagram of bird strike test platform

图2 平尾鸟撞工装Fig.2 Bird strike with flat tail worksuit

图3 鸟撞试验平台Fig.3 Bird strike test platform
试验中,将鸟体和弹托预先放入发射装置中,待控制气罐压力达到预定值并稳定后,开启压力阀,高压气体从控制罐进入发射腔,推动鸟体和弹托在炮管内滑行,经过弹托分离机构分离鸟体和弹托[26],鸟体撞击到固定在试验平台上的平尾。
2 鸟撞数值模拟
2.1 鸟体本构模型
鸟撞击靶结构的过程见图4[27],图中:V为鸟体速度;Vx为激波速度。鸟体撞击靶体过程会经历初始撞击、压力衰减、恒定流动和流动结束4个阶段,根据这种鸟撞特点,本文采用了文献[14]的经典鸟体本构模型,鸟体使用圆柱体模拟,长径比2∶1,鸟体参数见表1。空气参数见表2,在鸟撞冲击中,采用ESPOL多项式状态方程模拟鸟体:
(1)
式中:p为压力;e为单位质量的比内能;ρ为密度;ρ0为参考密度;a1~a6和b0~b1为自定义系数;μ=η-1,η=ρ/ρ0。
空气采用γ律状态方程定义:
p=(γ-1)ρe
(2)
式中:γ为比热比。
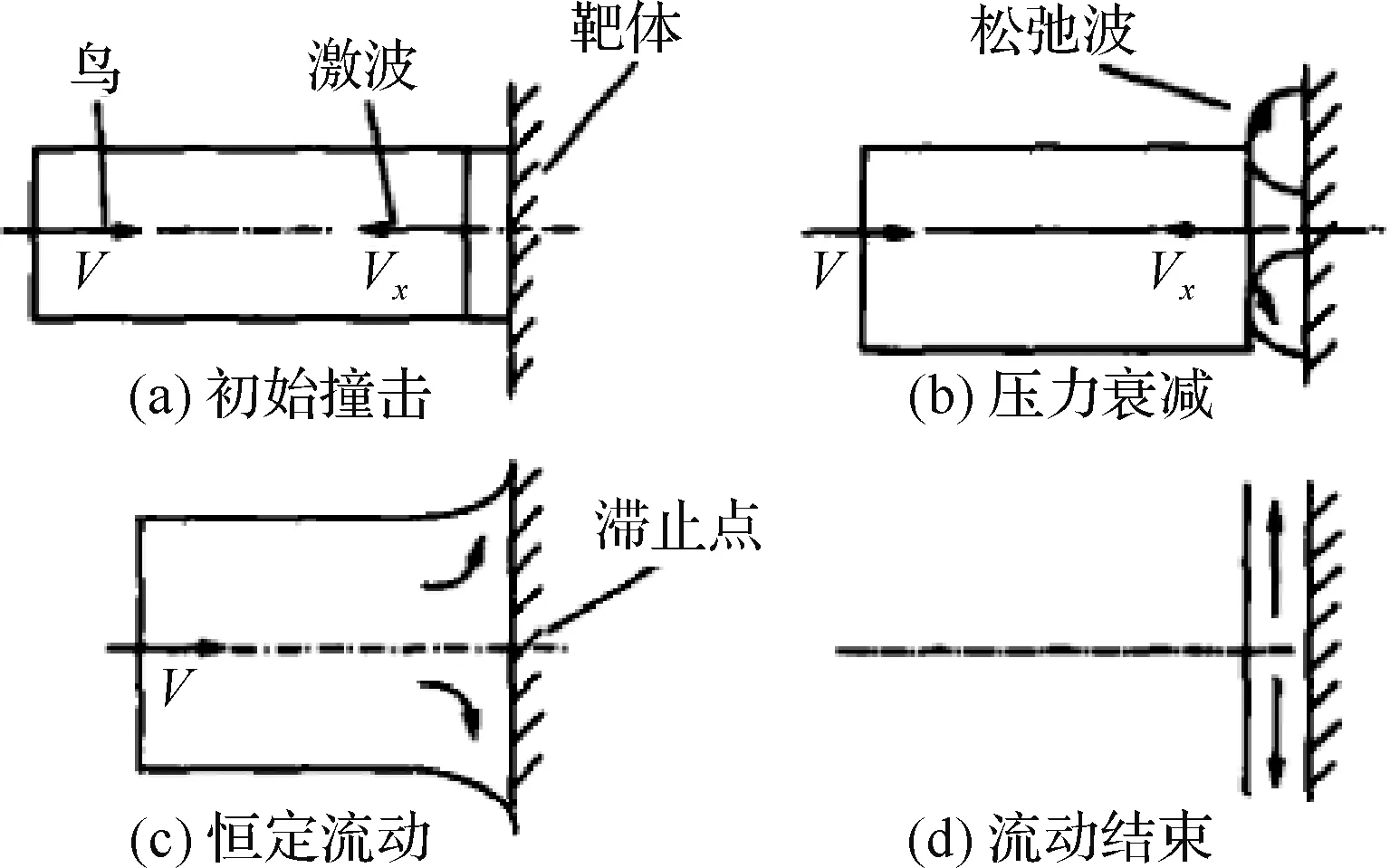
图4 鸟撞击靶体的4个阶段[27]Fig.4 Four stages of bird impacting target[27]
表1 鸟体参数
Table 1 Bird body parameters
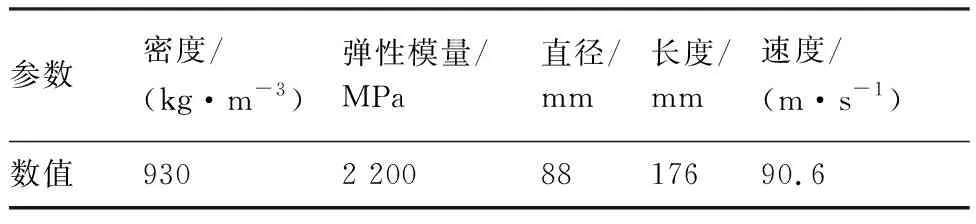
参数密度/(kg·m-3)弹性模量/MPa直径/mm长度/mm速度/(m·s-1)数值9302 2008817690.6

表2 空气参数Table 2 Air parameters
2.2 平尾有限元模型
平尾结构主要由小翼和平尾组成,通过接头与机体连接,如图5所示,平尾总体尺寸见图6。前缘和蒙皮是2024铝蜂窝结构,前后梁为机加7050铝梁,肋是2024钣金件铝板,各结构材料见表3。
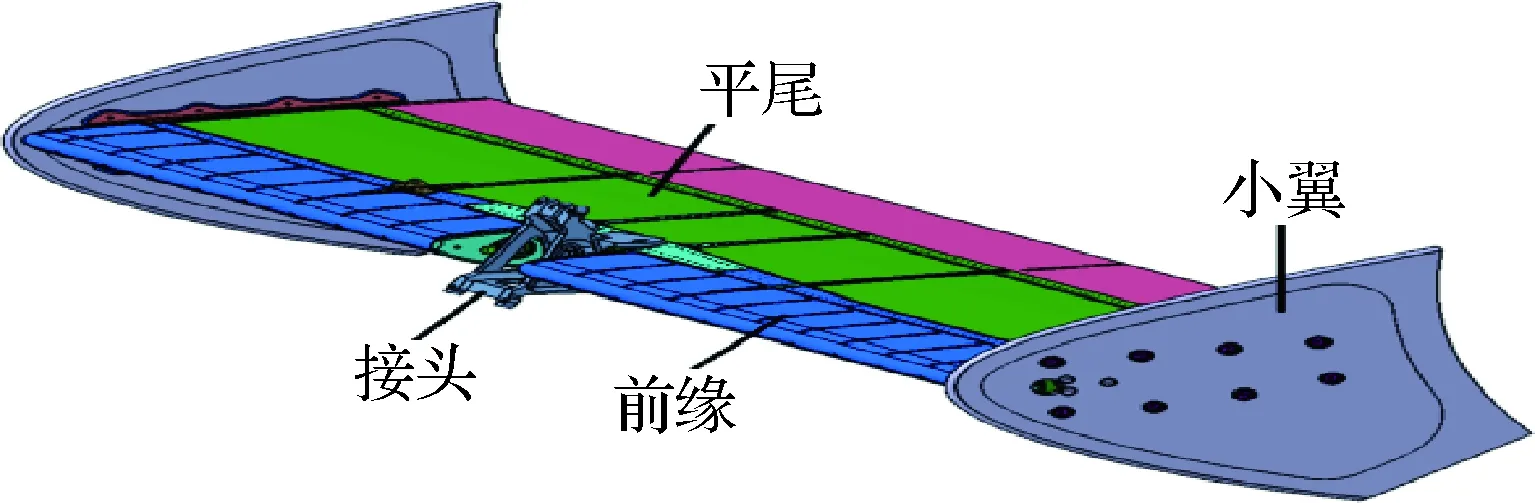
图5 平尾结构数模Fig.5 Numerical module of flat tail structure

图6 平尾尺寸Fig.6 Flat tail size
表3 结构材料Table 3 Structural materials

名称结构材料前/后缘蒙皮2024盒段[2024/蜂窝/2024]前/后梁7050肋腹板2024
对于金属,采用各向同性弹塑性本构模拟(DMATEP卡片),该本构还能够模拟双线性或分段线性的弹塑性行为,本文通过输入最大塑性应变值来控制单元失效,材料本构关系见图7,图中:E为弹性模量;σs为屈服极限。
纸蜂窝采用正交各向异性本构,使用蔡-胡失效准则判断失效:
(3)
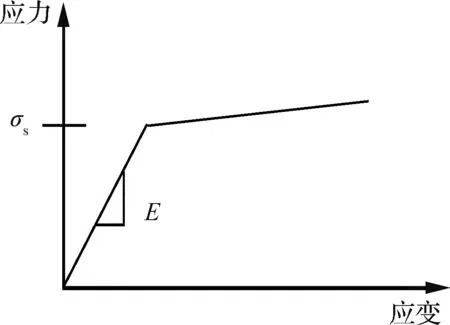
图7 弹塑性本构Fig.7 Elastoplastic constitutive
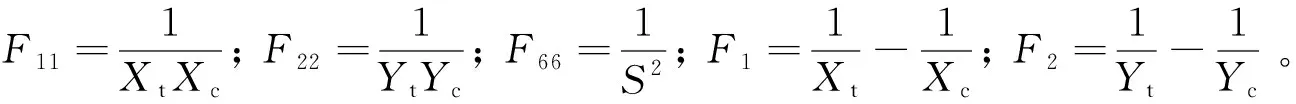
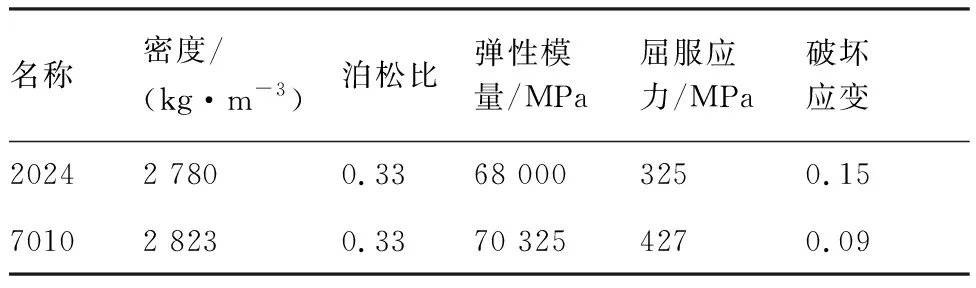
表4 铝材力学性能[28]Table 4 Mechanics properties of aluminum[28]

表5 蜂窝力学性能[29]Table 5 Mechanics properties of honeycomb[29]
平尾结构主要使用SHELL元模拟,共计26 000个单元,剖面图见图8。
由于图5中的小翼和接头对鸟撞影响较小,为了保证计算效率,在有限元模型中,平尾使用半对称模型,小翼与连接接头进行了省略,接头与平尾结构的连接使用约束X、Y、Z这3个方向平动来模拟,见图9。

图8 平尾有限元模型剖视图Fig.8 Section of finite element model with flat tail

图9 平尾有限元模型Fig.9 Finite element model of flat tail
2.3 流固耦合算法
流固耦合算法的目的是使欧拉网格与拉格朗日网格之间产生相互作用。两部分域各自的控制方程通过耦合面联立起来成为整个系统的控制方程组,这个方程组的求解是很困难的。所以在时间域上,程序采用数值方法,将整个时间段分解为一系列微小时间步,对2个系统分别迭代求解,求解时不考虑另一方状态的变化。
例如:先假定拉格朗日域在tn时刻的状态已知,在tn~tn+1时间步内,拉格朗日域的状态不发生变化。在固定边界条件下,对欧拉域求解,再将欧拉域内与耦合面相邻单元的压力作为载荷施加给拉格朗日单元。通过这种近似值的解法,对2个域轮流求解[30]。
由于鸟体在冲击平尾前缘时,鸟体碎片在穿透平尾前缘后,会对前梁结构造成二次冲击,故本文使用多欧拉域耦合(图10)的方法,对冲击过程进行模拟。在鸟撞的初始状态的定义中,平尾外部的空间域使用六面体欧拉网格定义,鸟体形状使用SHAPE卡片定义为圆柱体,前缘蒙皮和前梁之间的封闭空间使用自适应网格ADAPT卡片定义。当鸟体穿透前缘后,飞溅的碎片会通过内欧拉域网格继续与平尾结构发生作用,2个流体欧拉域使用空气定义,空气与鸟体与平尾结构存在的耦合关系见图10。
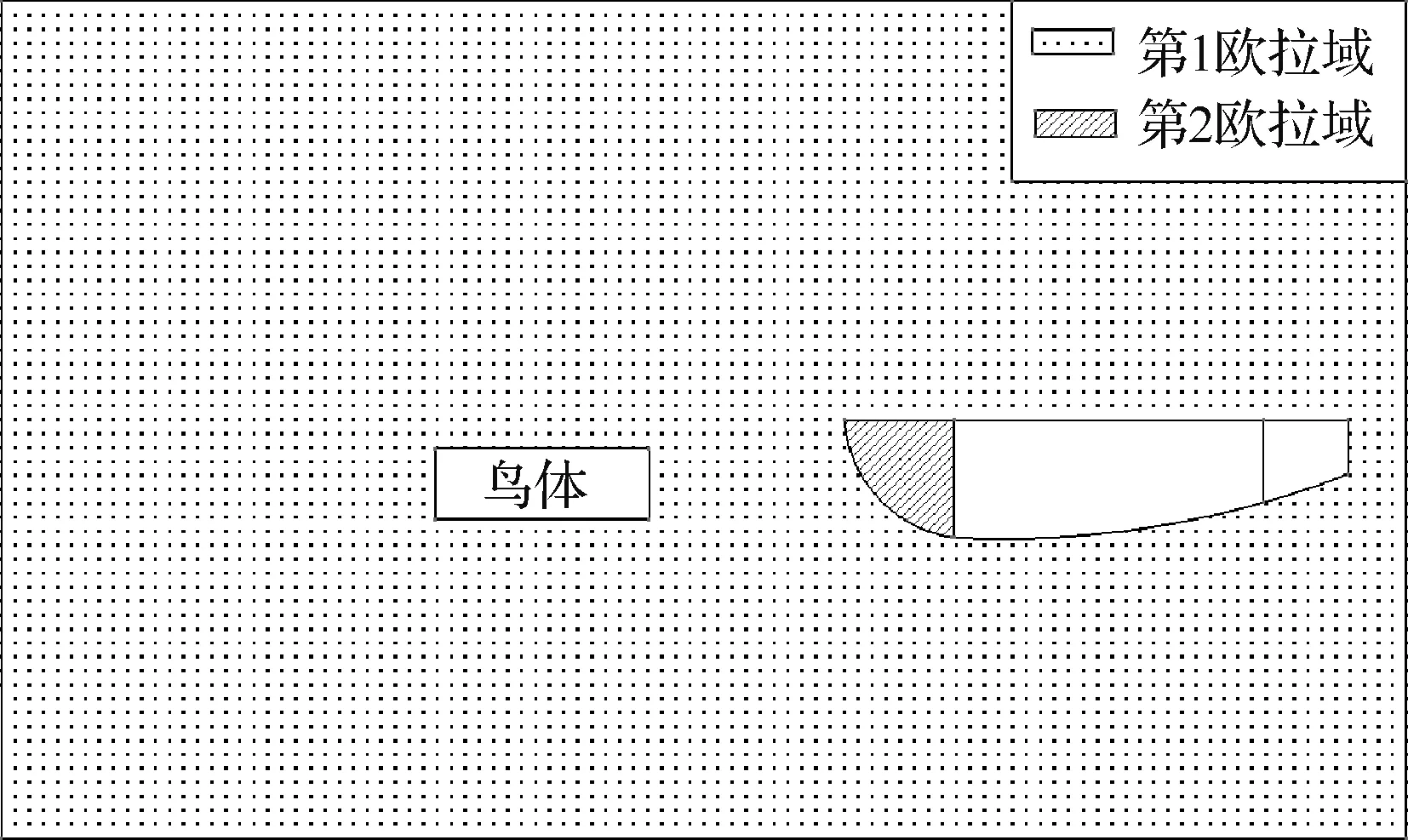
图10 鸟撞欧拉域示意图Fig.10 Diagram of bird strik Euler domain
3 计算结果讨论
3.1 结构损伤
鸟撞过程试验与仿真过程见图11和图12。在撞击中,鸟体穿透前缘蒙皮,对前梁造成二次鸟撞。鸟体逐渐破碎成细小的骨头和肉沫,其动态破坏过程表现为流体,因此表明用流体本构模拟鸟体是合理的;在鸟撞中不仅需要考虑撞击部位,还需要考虑到鸟撞发生后,鸟体是否会穿透撞击点对其他结构造成二次鸟撞。

图11 鸟撞试验录像截图Fig.11 Screenshot of bird strike test video
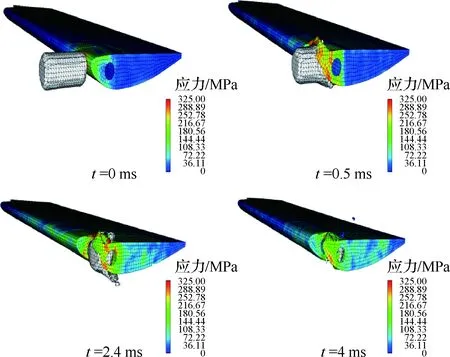
图12 鸟撞仿真过程Fig. 12 Bird strike simulation process
平尾损伤对比见图13,前缘蒙皮在鸟撞中出现了撕裂,前梁在鸟撞后出现凹坑,鸟撞点周围的蒙皮与肋出现严重变形。仿真与试验的失效形式基本吻合,由于在仿真中失效的单元会被删除,所以只能通过计算得到结构的失效位置和塑性变形,对于鸟撞后结构的损伤形状和撕裂形式模拟还有一定缺陷。

图13 鸟撞仿真与试验损伤对比Fig.13 Comparison of damage of bird strike simulation and test
3.2 鸟撞载荷
Barber和Boehman[31]通过试验研究了鸟体和刚体靶板的正撞击,测量了冲击载荷时程曲线,发现鸟撞载荷不仅与鸟体质量、鸟撞速度有关,与撞击结构也有关系,根据被撞击结构的不同响应,给出了理想刚体模型、局部刚体模型和局部变形模型。
理想刚体模型假设被撞击结构为刚体,在鸟撞中不发生整体的平动与转动;局部刚体模型假设撞击中有一定的平动与转动;局部变形模型假设被撞击结构在撞击中存在平动和转动,结构局部变形形成一个凹坑,鸟体陷入凹坑中,形成贝努利滞流压力。
通过计算发现,鸟体在冲击结构瞬间的载荷作用时长很短,在3 ms内就已完成对前缘蒙皮和前梁的冲击,见图14,鸟撞的位移测量点见图15,结构的位移响应对比见图16,从图中可知由于应力波传播速度的影响,在10 s后才会出现明显变形。
由图14可以看出,鸟撞前缘后,由于蒙皮被撕裂,载荷迅速衰减。鸟体冲击前梁时,载荷出现峰值,之后进入平缓区,逐渐衰减为0。
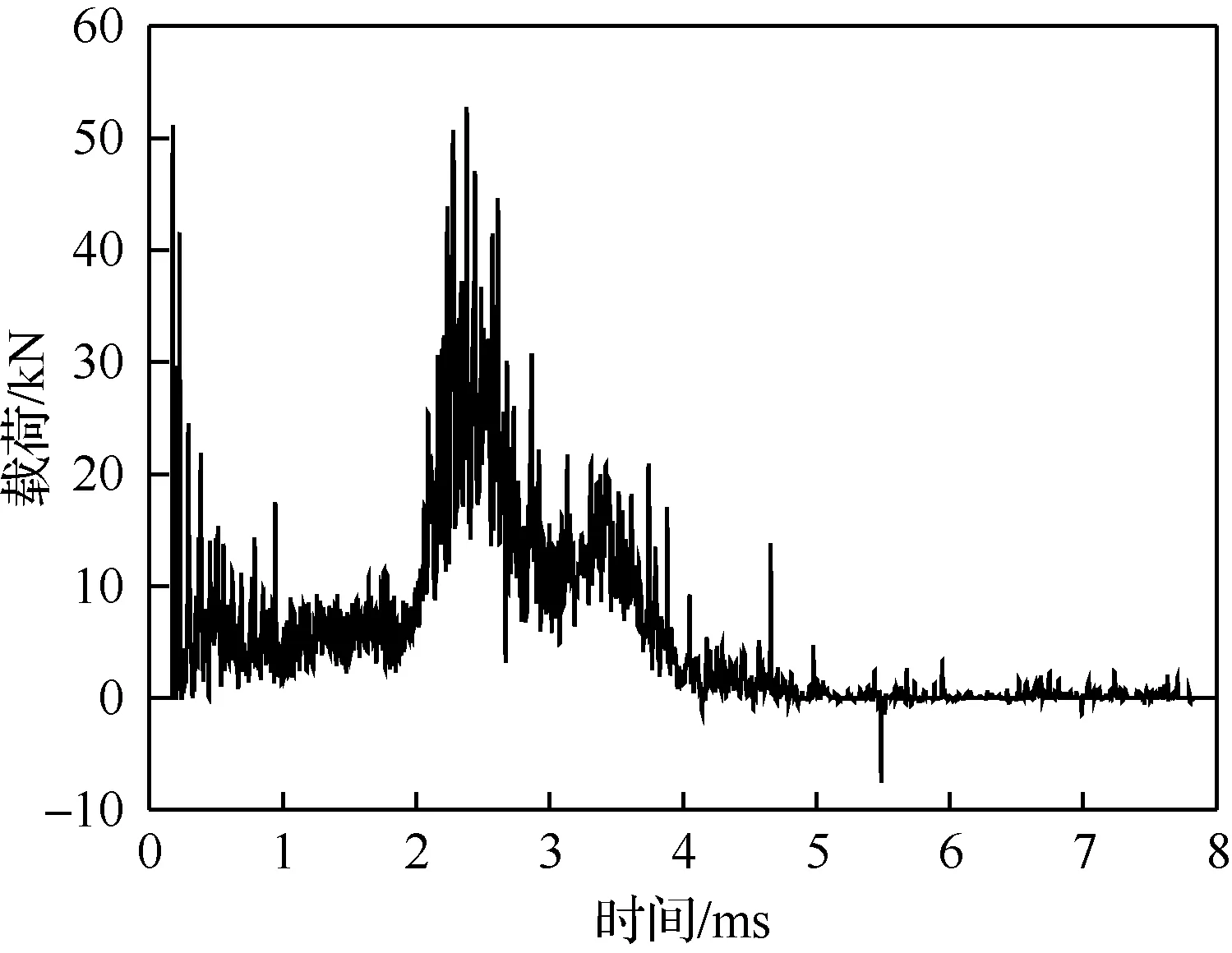
图14 鸟撞载荷随时间变化Fig.14 Variation of bird strike load with time
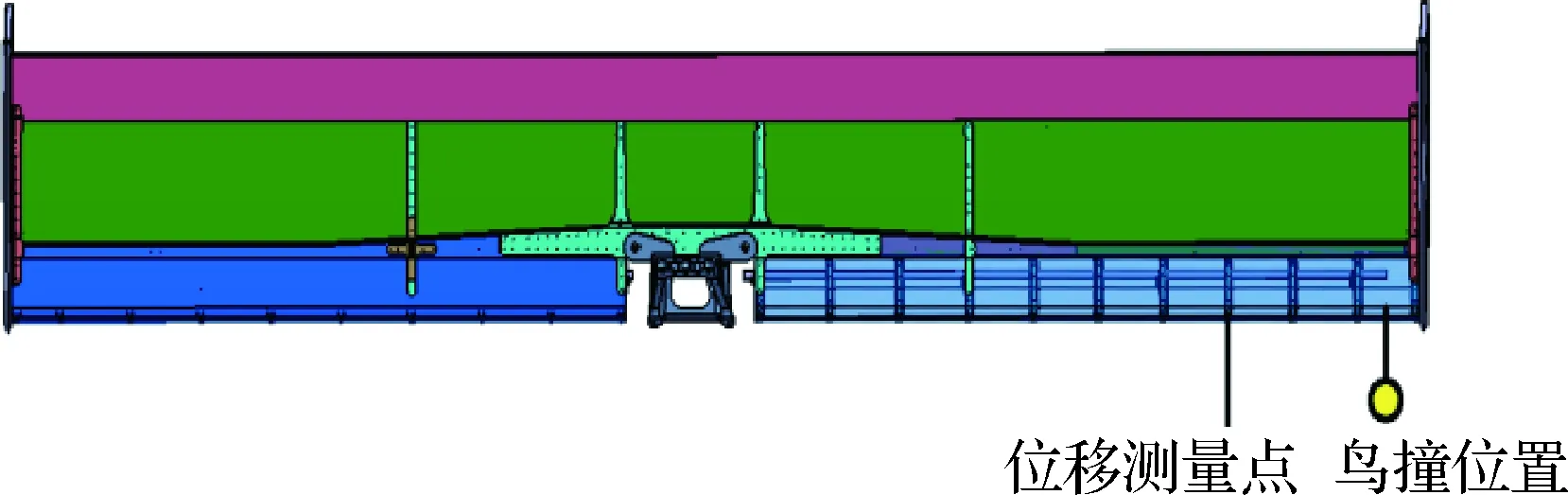
图15 位移测量位置Fig.15 Position of measurement of displacement

图16 仿真与试验变形值对比Fig.16 Comparison of deformation of simulation and test
这表明在第1次冲击瞬间,除冲击点外,整体结构并未发生明显位移变形。所以本文使用理想刚体模型的理论计算公式(见式(4)),假设在第1次冲击的瞬间,结构未发生整体变形,并与仿真值进行对比,结果见表6。
F=ρ1AV2sina
(4)
式中:ρ1为鸟体密度;A为鸟体截面积;V为鸟撞速度;a为鸟撞角度。F=930×0.0442×3.14×90.62×sin 90°=46 406 N

表6 冲击载荷仿真与理论值对比
以上分析表明,在鸟撞中,受到冲击失效的结构冲击载荷持续时间较短。而未发生失效破坏的结构,会受到连续性冲击载荷的影响,持续时间较长,危害性更大。
在此基础上,本文讨论了不同鸟撞速度下撞击载荷与平尾结构损伤情况,不同鸟撞速度下的撞击载荷和损伤对比如图17所示。
从图17可以看出,鸟体速度大于200 m/s时,平尾前梁2个端肋之间的梁腹板和上下蒙皮出现大面积损伤,2个端肋也出现了不同程度的破坏,肋的主要破坏部位在减轻孔周围,根部结构没有出现明显的损伤,但局部蒙皮结构出现了屈服现象,主要屈服位置是平尾前梁部位。不同鸟撞速度下的冲击载荷与损伤情况统计对比见表7和表8。
通过表7的对比可以发现,鸟体速度在小于50 m/s时对平尾结构的冲击没有出现明显损伤,但冲击载荷会随速度的提高明显增大。经验公式(4)的计算值明显小于数值模拟值,表明在小于50 m/s的低速冲击中,鸟体本构没有出现明显的流体性质,与文献[14]的结论一致。
在大于50 m/s的冲击中,冲击载荷的数值模拟结果与经验公式(4)的计算结果出现了一定的吻合趋势,50 m/s的单次数值模拟载荷大于经验公式计算值;90 m/s的单次鸟撞载荷与经验公式值基本吻合;150 m/s和200 m/s的前梁冲击载荷与经验公式值基本吻合;250 m/s的总鸟撞载荷与经验公式值基本吻合;300 m/s的数值模拟值小于经验公式值;以上现象表明经验公式在平尾鸟撞分析中受鸟撞速度影响,当速度小于200 m/s时,式(4)可用于对前梁结构的二次鸟撞载荷评估,当>200 m/s速度<300 m/s时可用于评估平尾鸟撞总载荷,当速度≥300 m/s,式(4)计算值较保守。

图17 速度20~300 m/s鸟撞载荷和损伤Fig.17 Load and damage at 20-300 m/s bird strike velocity
从表7、表8的对比结果可以看出:
1) 鸟撞总载荷具有明显的非线性特点,在本文没有考虑材料在高速冲击中的硬化和材料流动状态的情况下,总载荷并未随着速度的增大而线性增长。
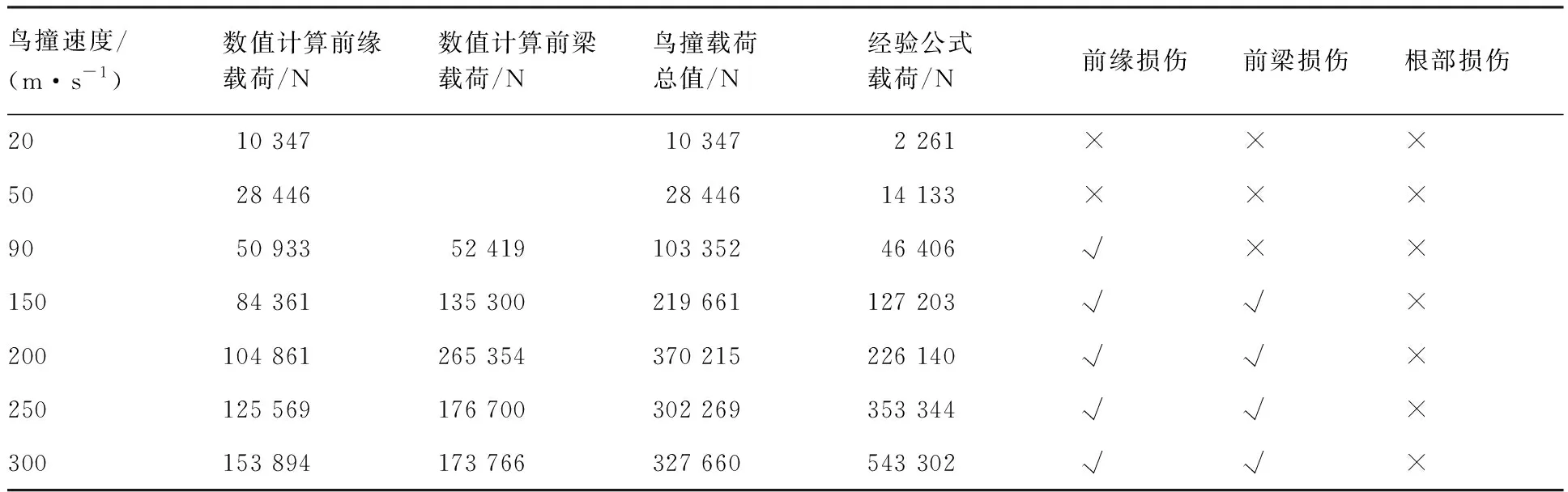
表7 不同鸟撞速度下的冲击载荷与损伤情况Table 7 Impact load and damage at different bird strike velocities

表8 不同鸟撞速度下的数值计算鸟撞载荷比值Table 8 Ratio of bird strike loads at different bird strike velocities for simulation
2) 在某些速度下,结构越“刚硬”,在鸟撞中产生的载荷越大。载荷峰值大小与受冲击的结构厚度有关,如本文中前梁厚度为1.5 mm,前缘蒙皮厚为前梁的40%,150~250 m/s鸟撞速度的前梁冲击载荷是前缘蒙皮的40%以上,但90 m/s和300 m/s鸟撞速度的载荷相当。
3) 对于第1鸟撞点前缘,在20~300 m/s的速度范围内,鸟撞载荷比值与速度比值的倍数基本吻合,且呈比例递增。
4) 对于第2鸟撞点前梁,其峰值大于第1鸟撞点,并具有非线性特点,当速度大于250 m/s时,载荷峰值出现衰减现象。
3.3 平尾根部响应
鸟撞冲击载荷,对平尾根部会产生很大的弯矩。为了研究冲击载荷对平尾根部的影响,本文在平尾根部上下蒙皮处位置粘贴了6个应变片,见图18,并在有限元模型的相应位置选取单元,与试验数值进行了对比。峰值误差对比见表9,应变时程曲线对比见图19~图21。

图18 平尾根部应变片位置Fig.18 Position of flat tail root strain gauge
表9 应变仿真与试验值对比
Table 9 Comparison of simulation and test results of strain

应变片仿真值试验值误差/%E7922.8921.70.1E81 117.21 003.111E9922.8784.817
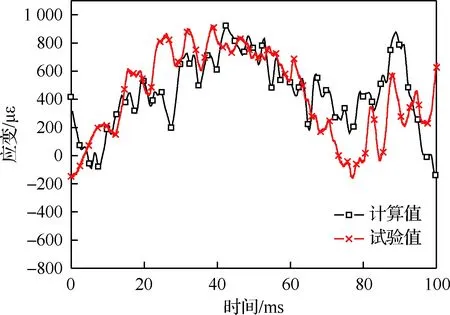
图19 E7位置应变试验与仿真值对比Fig.19 Comparison of E7 position strain between test and simulation values
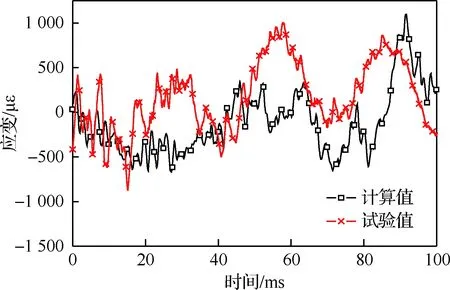
图20 E8位置应变试验与仿真值对比Fig.20 Comparison of E8 position strain between test and simulation values
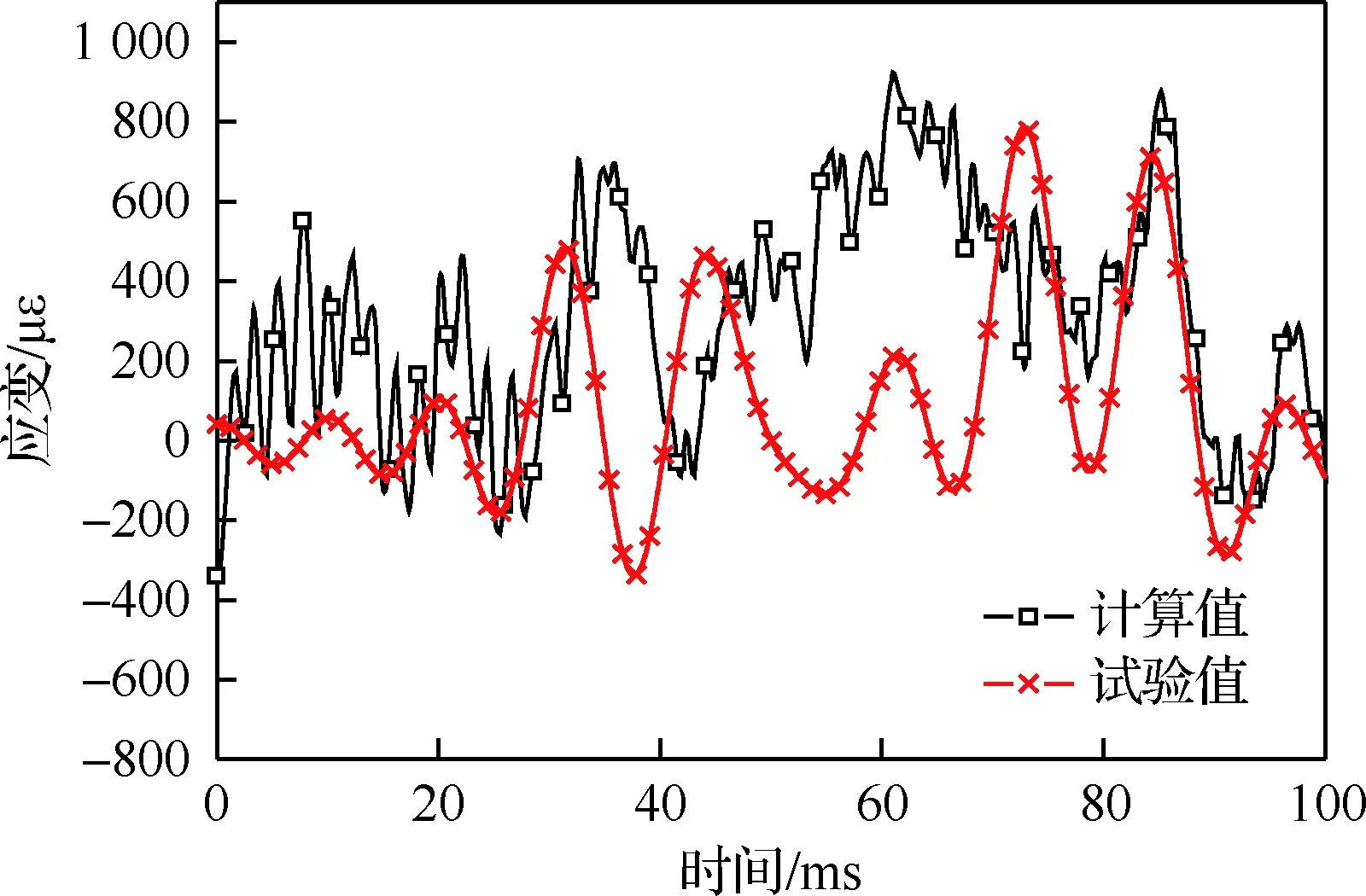
图21 E9位置应变试验与仿真值对比Fig.21 Comparison of E9 position strain between test and simulation values
从90 m/s速度的鸟撞载荷计算结果可以得到,在鸟撞产生了2次约为50 000 N左右的冲击载荷情况下,鸟撞部位至根部长度约为1 500 mm,由此产生的弯矩为75 000 N/m,但从表9的根部应变值对比可以看出,鸟撞后的根部响应应变峰值不高,平尾根部未发生撕裂性破坏,这表明平尾结构在鸟撞过程中前缘蒙皮和前梁结构起到了很好的吸能作用,消耗掉了大部分的冲击动能。
根据以上分析得到的鸟撞载荷特点,载荷时程曲线主要分为峰值区、平缓区和衰减区,见图22。

图22 鸟撞载荷模型Fig.22 Bird strike load model
4 结 论
1) 在平尾结构的鸟撞分析与试验中,除了鸟撞部位,还应考虑冲击载荷在平尾根部产生的附加弯矩对结构造成的影响,避免发生根部断裂。
2) 多欧拉域耦合法模拟鸟撞,能够准确地模拟鸟体对结构连续冲击的过程。鸟撞通常在几毫秒内完成,而结构响应由于应力波传递速率的影响,会出现明显的迟滞效应。
3) 如果鸟体在冲破第一结构后仍然保持完整,对第二结构的冲击仍会产生较大载荷,危害性较大。
4) 在平尾结构的抗鸟撞设计中,应预先对主要承力部件如:前梁、肋等结构的刚度值和材料选择进行测试,避免因材料过强或过弱导致在高速冲击中出现断裂,确保选择的材料在鸟撞中能够发挥一定的抗冲击和吸能作用。

