寻找“古典概型”与“几何概型”那片天地

周文国

在高中阶段，求解概率问题主要涉及的是古典概型和几何概型,对于这两类概型,要理解清楚其特点,才能灵活解题.其中古典概型的基本特征是有限性和等可能性，有限性是指在一次随机试验中,可能出现的结果只有有限个,即样本空间中基本事件只有有限个;等可能性是指在这个随机试验中,每个试验结果出现的可能性相等,即基本事件发生的可能性是均等的.几何概型的基本特征是无限性和等可能性，无限性是指在一次试验中,样本空间中基本事件有无限多个;等可能性是指在一次试验中,每个基本事件发生的可能性是相等的.

1 摸球问题

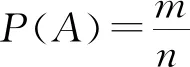
例1(1) 口袋中有6个除了颜色外其余全部相同的球,其中4个为白球,2个为红球,从袋子中任意取出2个球,求下列事件的概率:

(ⅰ)A={取出的2个球都是白球};

(ⅱ)B={取出的2个球中1个球是白球,1个球是红球}.

(2) 一个盒子里装有完全相同的10个小球,分别标上1,2,3,…,10这10个数字,现在随机抽取2个小球.

(ⅰ) 小球是不放回的,求2个小球数字为相邻整数的概率;

(ⅱ) 小球是有放回的，求2个小球数字为相邻整数的概率.

分析(1)中可先求出任取2个小球的所有等可能基本事件的总数,然后分别求出事件A“取出的2个球都是白球”所含的基本事件数及事件B“取出的2个球1个球是白球,1个球是红球”所含的基本事件数,最后再用古典概型的基本公式进行解答.

(2)是有放回与不放回的问题,其关键在于两者的基本事件总数是不同的.

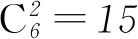
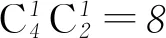
(2) 令“2个小球数字为相邻整数”为事件A.

点评 上述两类问题是摸球问题,一类是从中同时摸球问题,另一类是从中有序模球,涉及有放回与无放回问题,其关键是把基本事件总数及对应的随机事件数弄清楚.

2 排队问题

排队问题也是古典概型中的典型问题,其关键是注意排列数的正确计算,同时要分清楚基本事件总数和随机事件数.

例23男3女共6个同学排成一行,求下列事件的概率.

(1)甲同学不排在第一位;

(2)女生排在一起,男生排在一起;

(3)女生不相邻;

(4)女生和男生相间隔.

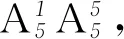
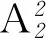
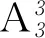
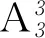
点评 对于排队问题,关键是正确利用分类、分步原理及排列组合知识求解随机事件的发生数和基本事件总数,然后再利用古典概型的计算公式使问题获解.

3 抛掷骰子问题

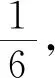
例3将一枚骰子连续抛掷两次,设第一次得的点数为x,第二次得的点数为y.

(1)求事件A：{两次点数之和等于8}的概率;

(2)若已知直线y=-3x+6与y=-x+4,求事件B：{点(x,y)在两已知直线下方}的概率.

分析(1) 将一颗骰子连续抛掷两次,基本事件总数有36种,两次点数之和等于8,可将随机事件数枚举;

(2) 点(x,y)在两直线的下方,故将满足条件的点(x,y)寻找出来即可.

解将一颗骰子连续抛掷两次,按其向上的点数不同,共有36种情况;

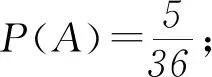
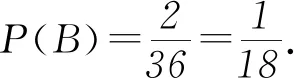
点评 本题研究的是简单的古典概型计算,古典概型具有等可能性，故可通过列表法列举出全部的基本事件,再进行分析,从而解决问题.

4 与函数结合问题

与函数相结合的概率问题是概率中常出现的题型,其关键是通过合理转化,利用古典概型或几何概型寻求解决.

例4已知关于x的一元二次函数

f(x)=ax2-2bx+8.

(1)设集合P={1,2,3}和Q={2,3,4,5},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间(-∞,2]上有零点且为减函数的概率.

(2)设集合P=[1,3]和Q=[2,5],分别从集合P和Q中随机取一个实数作为a和b,求函数y=f(x)在区间(-∞,2]上有零点且为减函数的概率.

分析(1)可利用列举法结合古典概型的概率公式进行计算;(2)可作出不等式组对应的区域,求出对应区域的面积,结合几何概型的概率公式进行计算.

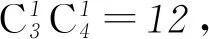
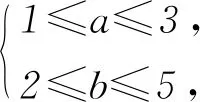
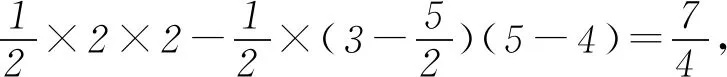
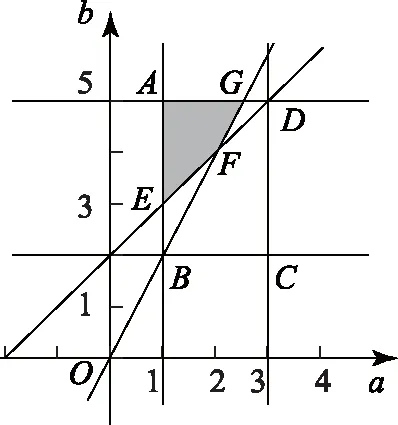
图1

点评 本题研究的是函数与古典概型、几何概型相结合的概率问题,其中利用列举法求古典概型以及利用数形结合法求解几何区域的面积是解决本题的关键.

5 相遇问题

相遇问题需要用两个连续变量来描述,用这两个变量的有序实数对来表示基本事件,再利用平面直角坐标系建立与面积相关的几何概型问题来求解.

例5某校早上8:10开始上课,假设该校学生小张与小王在早上7:30～8:00之间到校,且每人在该时间段内到校时刻是等可能的,求两人到校时刻相差10 min以上的概率.

分析设出小张与小王的到校时间分别为07:00后第x分钟,第y分钟,建立不等式组关系,求出对应区域的面积,结合几何概型的概率公式进行计算即可.

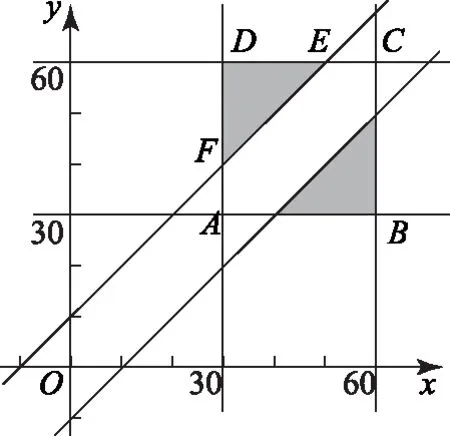
图2

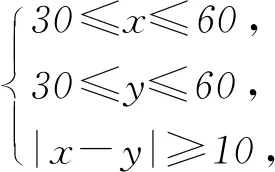
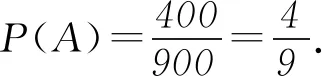
点评 本题研究的是计算几何概型,其关键是将实际问题转化为几何概型,借助区域面积求解.

6 与方程结合问题

几何概型常常与方程相结合,在解决这类问题时,需要借助方程的有关知识,找出满足条件的区域所包含的区间长度、面积大小或体积大小等.

例6已知关于x的一元二次方程9x2+6ax-b2+4=0,a，b∈R.

(1)若a是从1,2,3三个数中任意取的一个数,求已知方程有两个不相等实数根的概率;

(2)若a是从[0,3]内任意取的一个数,b是从[0,2]内任意取的一个数,求方程有实数根的概率.

分析本题中含有两个参数,需要将问题转化为含参数的一元二次方程有解的条件问题.(1)可利用列举法将基本事件罗列出来,再结合题意义解答;(2)可将a，b满足的不等式转化为图形,从而利用几何概型的概率公式求解.

解设“a是1，2，3中任意一个数，9x2+6ax-b2+4=0有两个不相等实数根”为事件A,“9x2+6ax-b2+4=0有实数根(其中a∈[0,3],b∈[0,2])”为事件B.

(1)由题意可知基本事件为9个,即(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示a的取值,第二个数表示b的取值.由Δ=36a2-36(-b2+4)>0,可得a2+b2>4,事件A要求a，b满足条件a2+b2>4,则包含6个基本事件,即(1,2),(2,1),(2,2),(3,0),(3,1),(3,2),事件A发生的概率

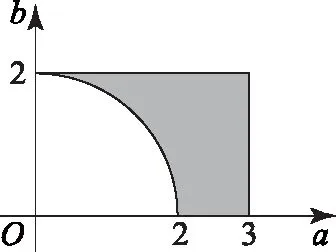
图3

(2)因为0≤a≤3,0≤b≤2,故构成的事件B的区域如图3中的阴影部分,其中a2+b2≥4,则所求的概率

点评 本题是方程与概率结合的问题,解题关键是分清楚用古典概型还是几何概型.

古典概型和几何概型是高中数学的重要知识点,其涉及的实际应用较多,解题关键是要准确识别两种概率类型,从而选择合适的方法及思路,走进“古典概型”与“几何概型”那片天地.