博弈视角下联合创新策略及协调机制研究
刘洪春 夏昊翔
(大连理工大学经济管理学院, 大连 116024)
引 言
上下游企业联合创新可以提高企业自主创新能力, 是实现企业创新的重要途径。 党的十八大以来, 以习近平为核心的党中央高度重视上下游协同创新, 鼓励上下游进行联合创新。 创新不仅需要大量研发成本投入, 还面临较高风险。 而上下游联合创新可以有效解决企业研发成本不足问题, 实现风险共享, 有利于促进创新。 上下游在协同创新时, 需要首先解决研发成本分摊问题。虽然上下游都投入了一定研发成本, 但是由于边际效应的存在, 使上下游研发成本投入不能达到最优效果。 因此, 研究上下游联合创新策略及协调机制具有重要的现实意义。
目前, 与本文相关的研究主要有两方面: 协同创新研究和协同创新协调机制研究。 针对协同创新的研究主要有: 陈劲等构建产学研协同创新博弈模型, 研究合作博弈策略“协同创新”、 “简单合作” 和“不合作” 对产学研协同创新的影响[1];李高扬等基于协同创新过程中策略演化过程, 构建产学研协同创新演化博弈模型, 研究得到, 产学研协同创新的均衡策略为4 种可能策略的组合[2];张喜征等构建企业创新下供应链博弈模型, 对比分析企业采取合作策略与不合作策略对企业收益的影响, 研究结果表明, 创新可以增加企业供应链利润, 创新投入成本与利润之间边际收益成负相关关系[3]; 张帆从多因素的角度, 运用博弈论分析技术创新激励的创新传导机制[4]; 王发明等运用动态博弈模型, 研究中小企业及创新企业合作创新的竞争机制, 研究得到创新生态系统中的领导企业可以采取优化分配机制、 提高自身声誉和选择吸收能力强的中小企业, 促进其合作[5]; 杨剑钊等揭示后发企业处于竞争劣势时如何达到超越在位企业进行技术创新策略的选择, 建立了博弈模型[6]; 蒋雪琳等构建了演化博弈模型, 基于知识投入研究企业合作创新的路径问题, 认为经过长期演化, 企业有两种策略选择: 合作策略和不合作策略[7]。
针对协同创新协调机制的研究主要有: 梁双陆等构建产业创新、 技术创新和组织创新指标体系, 比较中国东部、 中部和西部创新发展水平,并给出东部、 中部和西部协调创新机制[8]; 龙跃等从知识生态转化角度, 融合博弈论、 效用论和知识生态学等理论构建知识生态转化的产业创新主从协调模式, 揭示核心组织在知识资源配置过程中双重协调机理[9]; 邹艳等通过调研, 并做出实证研究认为, 协调机制对学习动机的中介作用大于学习能力[10]; 王海军等研究产学研进行协同创新时的知识转移协调机制, 认为模块化有利于产学研三方的协同创新[11]。
综上所述, 目前针对协同创新及协调机制的研究已经取得较大成就, 如基于博弈论研究协同创新, 得到协同创新机制与政府如何激励协调创新[1-7]; 从空间角度、 知识转移角度研究协同创新协调机制[8-11]。 但是, 针对创新研发成本分摊成本问题鲜有研究。 因此, 本文基于研发费用承担模式, 构建上下游联合创新的博弈模型, 并进一步研究上下游实现协同创新的机制, 为实现上下游协同创新提供决策依据。
1 问题描述与假设
1.1 问题描述
基于上下游同时承担研发费用, 构建由一个研发企业和一个生产企业组成的上下游协同创新博弈模型。 其中, 研发企业只负责研发, 并承担一定研发费用, 生产企业负责生产, 同时, 为进一步促进研发企业研发, 愿意承担一定研发费用。最后, 为进一步实现上下游联合研发达到最优,研究上下游协调创新机制。
决策顺利: 首先决策上下游研发费用, 其次是研发企业决策单位产品委托研发费用, 最后是生产企业根据单位产品委托研发费用决策单位产品零售价格。 根据博弈论逆序求解可知, 在求解时, 首先决策单位产品零售价格, 其次决策单位产品委托研发费用, 最后决策研发费用。
1.2 符号说明
上标D: 表示分散决策情形;
上标C: 表示集中决策情形;
wD: 单位产品委托研发费用;
pi: 情况i 下, 单位产品的销售价格, 其中i∈{D,C};
1.3 模型假设
(1) 借鉴徐春秋等的研究[12], 研发企业创新成本与创新努力程度的关系为: 研发创新 其中γY=0, 表示研发创新努力成本系数; 生产企业创新成本与创新努力程度(t)关系为: 生产企业创新努力成本其中γS表示生产企业创新努力成本系数。
(2) 借鉴Liu 等、 Gurnani 等的研究[13,14], 需求函数为:
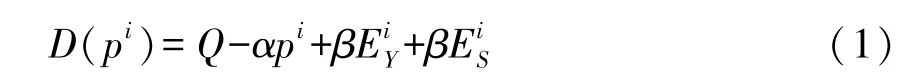
其中i∈{D,C}, Q 表示市场上对产品的潜在需求量, α>0 表示消费者对单位零售价格p 反映系数, β>0 表示消费者对创新努力程度反映系数,根据实际情况可知α>β。
2 模型分析
2.1 分散决策下
研发企业目标函数为:

其中wD-c 表示研发单位产品获得收益, (wDc)表示研发企业的总收益,表示创新成本。
生产企业目标函数为:

其中pD-wD表示销售单位产品获得收益, (pDwD)(Q-αpD++)表示生产企业的总收益,表示创新成本。
为了下面便于求解, 首先给出引理1。
引理1: 式(3) 关于pD、 EDS 是凹函数, 根据式(3) 求得的解带入式(2) 后, 式(2) 关于wD、是凹函数。
证明: 对式(3) 关于pD、求一阶、 二阶偏导数可得:

式(3) 关于pD、的海塞矩阵为:

引理得证。
由式(4) 和(5) 可得:


由此可得结论1, 上下游创新努力对单位产品委托研发价格、 单位产品零售价格、 需求量和收益具有影响, 具体见结论1。
结论1: 分散决策时, 创新努力程度对单位产品委托研发费用、 零售价格和需求量影响为:
证明: 结论(1) 由式(7) 可得:

类似可证其它结论成立。
结论1 证毕。
结论1 表明研发企业进行创新时, 会通过提高单位产品委托研发费用来转移其研发成本。 当消费者对价格敏感度小于某一阀值(该阀值与消费者对创新努力程度敏感性和创新成本系数有关) 时, 单位产品委托研发费用、 需求量与生产企业单位创新努力程度正相关, 否则为负相关。单位产品零售价格与单位产品创新努力程度正相关、 产品需求量与单位研发企业创新努力程度正相关。
管理启示: 虽然单位产品委托研发费用与研发企业单位创新努力程度正相关, 但研发企业进行创新时有利于促进产品销售。 因此, 生产企业应为研发企业提供资金支持, 鼓励研发进行积极创新。
由引理1, 可得结论2。
结论2: 分散决策时, 最优纳什均衡解为:

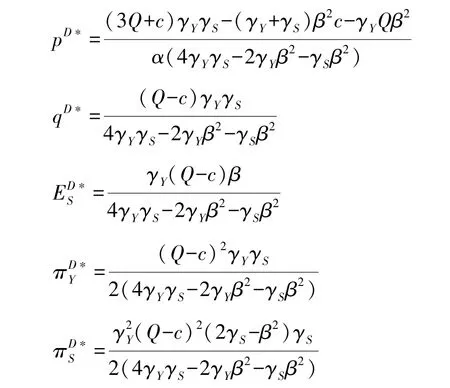
2.2 集中决策时

类似于分散决策, 可得结论3。

结论3: 集中决策时, 最优纳什均衡解为:为便于讨论记为:由结论2 和结论3 可得结论4, 具体如下:

结论4: 分散决策与集中决策对创新努力程度、 单位零售价格和收益影响:
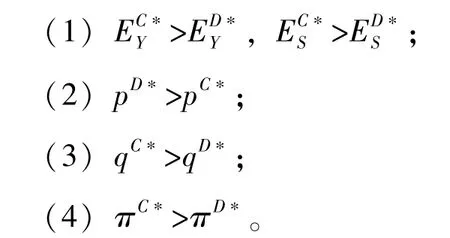
类似可证其他结论成立。
由结论4 可知, 集中决策时单位产品零售价格小于分散决策时单位产品零售价格, 集中决策时产品销售量大于分散决策时产品销售量, 集中决策时创新努力程度大于分散决策时创新努力程度, 集中决策时收益大于分散决策时收益之和。主要原因: (1) 集中决策时, 单位产品零售价格小于分散决策时单位产品零售价格, 间接促进销售者购买积极性, 增加产品销售量, 即集中决策时, 产品销售量大于分散决策时销售量; (2) 虽然集中决策时, 单位产品收益减少, 但是, 产品销售量增加带来收益大于单位产品带来收益减少量, 即人们常说的“薄利多销”。
通过结论4 可知, 集中决策时可以避免研发企业与生产企业的边际效应, 增加收益。 因此,有必要研究研发企业与生产企业协调策略, 使其避免边际效应, 最终使上下游收益达到整体最优。下文给出上下游创新协调机制。
2.3 收益共享契约协调机制
该契约中, 要求研发企业以较低的单位产品委托研发费用将研发技术提供给生产企业, 在特殊情况下, 该单位产品委托研发费用小于或等于单位产品研发成本。 但生产企业为弥补研发企业的收益损失, 需要按一定比例向研发企业分享其销售收益。 此外, 生产企业还应按照一定比例承担研发企业的创新成本, 同时, 研发企业也需要按照某一比例承担生产企业创新成本。 在此, 设生产企业按比例φ 将其收益分享给研发企业, 同时, 按比例ξ 对研发企业创新成本进行承担, 且研发企业按比例ψ 对生产企业研发成本进行承担。 根据实际情况可知: φ∈[0,1], ξ∈[0,1],ψ∈[0,1]。
根据上述描述, 可得在收益共享契约协调机制下, 研发企业和生产企业的收益函数为:

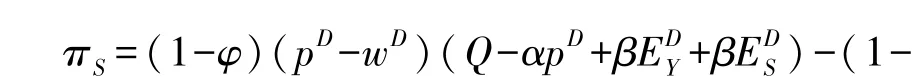

结论5: 当w*=c 且φ=ξ=ψ 时, 联合创新达到协调, 其中φ=ξ=ψ 满足下列条件:

证明: 类似结论1, 由式(9) 可得:


将p**、 E**S带入式(8) 可得:
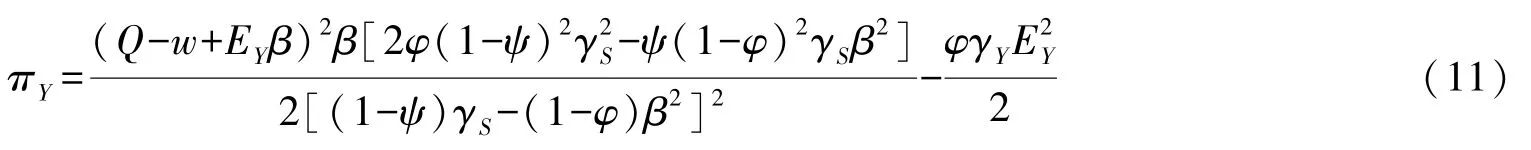
将w**=c 带入式(11), 然后对式(11) 关于EY求解可得:

将w**、带入p**、可得:

通过p**、与pC*、对比可知当φ=ξ=ψ有pC*=p**,=E,=, 即这时生产企业与研发企业达到协调。

3 数值分析
为了更详细与直观分析创新努力成本系数对纳什均衡解影响, 运用MatlabR2014a 进行仿真分析, 借鉴王海军等的研究[11], 取Q=100, β=2,c=20。
3.1 对研发费用与研发努力程度的影响
由图1 可知, 分散决策时, 单位产品委托研发费用与创新努力成本系数负相关, 且研发企业创新成本系数对单位产品委托研发费用影响不是很显著, 生产企业创新努力成本系数对单位产品委托研发影响较显著。 主要是因为研发企业可以通过单位产品研发费用转移研发成本给生产企业。由图1 并结合分析可得推论1。

图1 创新努力成本系数对单位委托研发费用的影响
由图2 可知, 集中决策时研发企业创新努力程度显著大于分散决策时研发企业创新努力程度,且创新努力程度成本系数对研发企业创新努力程度的影响在集中决策时较明显, 即集中决策时,研发企业创新努力程度对创新努力成本系数较敏感。 主要原因是集中决策时, 不仅可以减少边际效应, 还可以进一步促进企业研发努力积极性,分散决策时, 研发企业与生产企业只关注自身收益而忽略整体收益, 因此对创新努力成本系数较少关注。 由图2 和分析可得推论2。

图2 创新努力成本系数对研发企业创新努力程度的影响
推论2: 创新努力成本系数对研发企业创新努力程度的影响为:
3.2 对收益的影响
另外, 创新努力成本系数对生产企业创新努力程度、 需求量的影响与对研发企业的影响大致一样, 在此, 就不给予仿真分析。

图3 创新努力成本系数对研发企业收益的影响

图4 创新努力成本系数对生产企业收益的影响
由图3 和图4 可知, 研发企业创新成本系数对研发企业收益影响不是很明显, 即其收益变化趋势不是很明显, 且研发企业收益与研发企业创新成本系数负相关, 但是研发企业创新成本系数对生产企业的收益的影响较明显, 且生产企业收益与研发企业创新成本系数正相关。 无论是研发企业还是生产企业, 生产企业创新成本系数对其收益的影响是正的, 且生产企业创新成本系数对生产企业收益影响较显著。 根据上述分析, 再结合图3 和图4 可得如下推论3。
4 研究结论
为分析研发企业与创新企业协同创新, 构建上下游联合创新的博弈模型。 基于此博弈模型,分析研发创新努力成本系数对创新努力程度、 单位委托研发成本、 单位产品销售价格、 销售量和收益的影响, 并进一步研究上下游协同创新协调机制, 研究主要得到结论如下:
(1) 研发企业进行创新时, 会通过提高单位产品委托研发费用来转移其研发成本; 单位产品零售价格与单位产品创新努力程度正相关、 产品需求量与单位研发企业创新努力程度正相关。
(2) 分散决策时, 单位产品委托研发费用与创新努力成本系数负相关, 且研发企业创新成本系数对单位产品委托研发费用影响不是很显著,生产企业创新努力成本系数对单位产品委托研发影响较显著。 集中决策时单位产品零售价格小于分散决策时单位产品零售价格, 集中决策时产品销售量大于分散决策时产品销售量, 集中决策时创新努力程度大于分散决策时创新努力程度, 集中决策时收益大于分散决策时收益之和。
(3) 研发企业创新成本系数对研发企业收益影响不是很明显, 即其收益变化趋势不是很明显,且研发企业收益与研发企业创新成本系数负相关,但研发企业创新成本系数对生产企业的收益影响较明显, 且生产企业收益与研发企业创新成本系数正相关。

