中国高新区收入差距、 全要素生产率及其收敛性研究

孙红军 王胜光

1 (中国科学院科技战略咨询研究院, 北京 100190)

2 (中国高新区研究中心, 北京 100190)

引 言

自1988 年中关村设立以来， 经历了30 多年的发展， 中国国家高新区极大发挥了对我国技术创新和产业升级的“示范、 引领、 辐射、 带动” 作用， 尤其是在促进我国实现创新发展方面取得了引人注目的成就。 据统计， 2017 年全国国家高新区国家级科研机构约占全国的66.7%， 高新技术企业占全国高新技术企业数量的38.4%， 企业R＆D经费支出占全国企业R＆D 经费总支出的50.6%；PCT 专利占全国的31%， 高新技术产品出口总额占全国的41.7%， 生产总值达到9.76 万亿人民币，相当于俄罗斯的GDP (1.58 万亿美元）［1］。 由此可见， 国家高新区本质上体现了科技与经济深度融合， 是典型的创新经济形态， 呈现出了明显的创新驱动发展特征。 目前， 我国经济已由高速增长阶段转向高质量发展阶段， 提高全要素生产率(Total Factor Productivity， TFP） 是经济高质量发展的动力源泉。 国家高新区作为我国高质量发展的典型代表， 是引领和带动我国发展方式转变、经济结构优化、 增长动力转换的前沿阵地， 着力推动着我国经济增长方式由投资驱动向创新驱动和全要素生产率驱动转变。 因此， 准确识别全要素生产率是否已经成为国家高新区经济差距的决定力量， 并深入探究国家高新区全要素生产率与收入的收敛模式是值得研究的重大问题， 对提升国家高新区经济增长质量与推动区域经济协调发展具有重要的理论价值和现实意义。

有关TFP 是否成为区域经济发展差距主要力量的研究一直是国内学术界关注的热点。 就研究对象而言， 现有研究主要关注TFP 与省际层面经济发展差距的关系问题。 基于此， 本文将研究视角由省际转向国家高新区层面， 探究全要素生产率是否已经成为国家高新区经济差距的主要原因。主要研究方法有： (1） 采用方差分解方法， 如彭国华［2］、 李静等［3］、 傅晓霞和吴利学［4，5］均采用了方差分解方法分析中国省份的全要素生产率与地区收入差距问题； (2） 非参数回归方法， 刘华军等［6］采用QAP 相关和回归分析探究了中国省份的全要素生产率与地区差距关系， 但QAP 分析方法极易受到控制变量的影响， 不同控制变量有可能会直接影响TFP 对经济差距贡献的大小甚至是作用方向。 基于此， 本文将借鉴彭国华、 李静等、傅晓霞等的做法［2－5］， 采用方差分解方法来测算TFP 对国家高新区收入差距的贡献。

此外， 就目前仅有的关于国家高新区TFP 的研究而言， 程郁等［7，8］采用超越对数随机前沿生产函数测算了2002 ～2010 年52 个国家高新区TFP，并指出TFP 对经济增长的贡献相对较低。 然而，该研究仍需从以下方面进行完善： (1） 该研究主要关注国家高新区TFP 测算及TFP 对经济增长的贡献问题， 而非关注TFP 对国家高新区经济差距的贡献； (2） 该研究在测算TFP 时采用的是超越对数随机前沿生产函数， 而后续测算TFP 贡献率时则是基于C－D 生产函数框架来进行的， 这样就导致了测算的TFP 贡献率偏离了实际情况(如测算结果显示： 吉林高新区TFP 对经济增长的贡献率高达59.48%， 远远高于中关村36.19%的贡献率， 这种结果显然与实际情况不相符）； (3） 限于样本数量和时间， 该研究以2002 ～2010 年“二次创业” 阶段①的52 个国家高新区为研究对象，由于国家高新区是在“二次创业” 阶段开始注入创新要素， 并逐步强调产业升级和技术创新重要性， 使得这一阶段高新区创新经济发展特征并不明显， 国家高新区“三次创业” 则进入了全面创新阶段， 创新经济特征日益显著， 如采用这一时间段内的样本数据进行分析则更能说明问题。 基于上述原因， 现有研究无法准确、 真实地反映出TFP对高新区收入差距的贡献情况。

国内外学者也对TFP 与收入的收敛模式进行了分析， 如Bernard 和Jones［9］对OECD 国家的不同产业TFP 和收入模型进行分析； Miller 和Upadhyay［10］对不同国家间TFP 与收入的收敛性质进行研究； 彭国华［2］、 屈小娥［11］则对中国省份及不同区域TFP 与收入的收敛情况进行了探究； 李卫兵和涂蕾［12］则分析了中国城市层面TFP 的收敛性。 通过对上述有关区域层面的TFP 与收入收敛分析可知， 目前有关国家高新区层面的TFP 与收入的收敛分析的研究相对较少。

为弥补上述文献不足与缺陷， 本文以2011 ～2017 年88 个国家高新区为研究对象， 在测算了88 个国家高新区TFP 的基础上， 采用方差分解方法分析了TFP 对国家高新区收入差距的贡献率；依次采用OLS 回归和Panel Data 固定效应对TFP与收入进行了收敛分析。

1 研究方法

1.1 全要素生产率的测算及分解

本文采用索罗余值方法来测算国家高新区全要素生产率， 假定生产函数为C－D 形式， 如式(1） 所示：

其中， Yit表征国家高新区i 在t 年的收入，Kit和Lit分别表征国家高新区i 在t 年对应的资本投入和劳动投入， α 和1－α 分别表征资本和劳动要素的产出弹性， Ait为全要素生产率。 由式(1）可知， 计算资本要素投入的产出弹性α 是计算全要素生产率的关键。 目前研究中一般是根据各要素在总收入中的份额或参数回归方法测算各要素在总投入中的份额［2］。 本文则采用参数回归法来估计资本要素投入的产出弹性(本文测算结果：α=0.4347）。 进一步将式(1） 两边同时除以L可变形为式(2）：

其中， yit=Yit/Lit， 表征高新区i 在t 年的劳均收入， kit=Kit/Lit， 表征高新区i 在t 年的劳均资本。 之所以将式(1） 变形为式(2）， 是因为劳均收入衡量区域经济发展水平更具科学性， 更能反映一个区域经济福利情况。 对式(2） 两边同时取对数， 可变形为式(3）：

其中， TFPit=Ait， 即全要素生产率水平，为资本要素投入。 式(3） 表示可将劳均收入分解为全要素生产率和资本要素投入。 因此， 进一步可将两个国家高新区i 和j 在t 时期的收入差距分解为以下两个部分：

为进一步探究全要素生产率与资本要素投入对收入差距的贡献及其演变趋势， 本文对劳均收入进行KR 方差分解(该分解方法由Klenow 与Rodriguez－Clare 于1997 年提出， 为便于分析， 本文简称KR 分解）：

此外还可以进行EL 分解， 并将劳均收入分解为要素投入差距、 全要素生产率差距以及两者协方差三部分(该分解方法由Easterly 与Levine 于2001年提出， 为便于分析， 本文简称EL 分解）：

由此， 根据式(5）～(8） 就可以测算全要素生产率与资本要素投入对国家高新区经济发展差距的贡献率。

1.2 收敛分析方法

一般而言， 主要有3 种收敛形式： σ－收敛、绝对β－收敛以及条件β－收敛。 σ－收敛较为简单，主要是利用样本的标准差进行收敛判定， 判定原则是： 如果标准差随时间减小就存在σ－收敛， 直接反映样本间的经济发展差距在逐步缩小。

绝对β－收敛是指不同高新区的总收入和全要素生产率最终都会达到相同增长水平和增长速度，我们将采用回归方法分析绝对β－收敛， 具体测算方程如式(9）、 (10） 所示：

其中， yite、 TFPite分别为样本考察期内i 高新区最后一期的劳均收入与TFP， yitb、 TFPitb分别为样本考察期内i 高新区第一期的劳均收入与TFP，即样本结束时间和开始时间样本值， T 为结束和开始两个时间点相隔的年数。 如果β 显著为负，就存在绝对β－收敛， 收敛速度λ 可以根据Mankiw 等［13］提出的计算方法进行计算， 具体计算公式如下所示：

条件β－收敛与绝对β－收敛不同， 它是指每个高新区都有自己的基础和特点， 会朝着自身的稳态水平趋近。 因此， 条件和绝对β－收敛虽然都是趋向稳态， 但两者区别较大， 绝对β－收敛是所有高新区趋向相同的速度和水平， 条件β－收敛反映每个高新区趋向于自身的稳态水平。 如果β 显著为负， 就存在条件β－收敛， 根据Miller 和Upadhyay［10］的研究可知， Panel Data 固定效应估计方法是进行条件收敛的一个简洁方法， 它通过设定截面和时间固定效应， 不仅关注了每个个体不同的稳态值， 而且也关注了个体稳态值随时间的变化态势。 本文检验条件收敛的公式如下所示：

其收敛速度λ 用下式表示：

1.3 研究对象与数据来源

考虑到数据的准确性和可获得性， 为进一步分析国家高新区全要素生产率的贡献演变及其收敛情况， 并结合国家高新区2010 年之后进入全面创新阶段， 本文选取2011 ～2017 年88 个国家高新区作为研究对象， 并按照区域发展战略， 将88家高新区按照其所属地域划分为东部、 中部、 西部以及东北部国家高新区， 具体划分结果如表1所示。

表1 88 个国家高新区分布表

由于测算全要素生产率会涉及高新区产出、要素投入等相关指标， 本文以高新区营业收入作为期望产出， 以年末资产合计(火炬统计有标准口径的资产合计指标， 避免了因统计口径不一致和不同折算方法而带来的资本存量误差） 作为资本投入， 以年末从业人员作为劳动投入。 以上数据均来自于国家统计局与国家科技部火炬高技术产业开发中心火炬计划的统计数据。

2 实证分析

2.1 贡献率分析

表2 报告了国家高新区收入差距来源的KR与EL 分解结果， 由表2 可以看出， 无论是KR 还是EL 分解， TFP 对高新区劳均收入差距的贡献远远大于资本的贡献， TFP 贡献约是资本贡献的2.5 倍。 具体而言， ER 分解结果显示， TFP 贡献为71.325%， 资本投入的贡献为28.675%； EL 分解结果显示， TFP 贡献为70.575%， 资本投入的贡献为27.926%。 由此可知， TFP 而非资本投入是造成高新区经济发展差距的主要原因。 从贡献率演变趋势看， 以2014 年为分界点， 全要素生产率贡献率整体上呈现出先上升后下降的趋势， 而资本贡献率则呈现出先下降后上升趋势， 可能原因是国家高新区从2014 年之后开启了大规模开发与扩区建设， 据统计， 2011 ～2014 年高新区(88 家国家高新区） 实际开发的土地面积仅增长了184.056平方公里， 而2015～2017 年高新区实际开发的土地面积增长了905.341 平方公里， 原因就是高新区这种大规模的开发投资活动可能会持续拉低全要素生产率的贡献率。

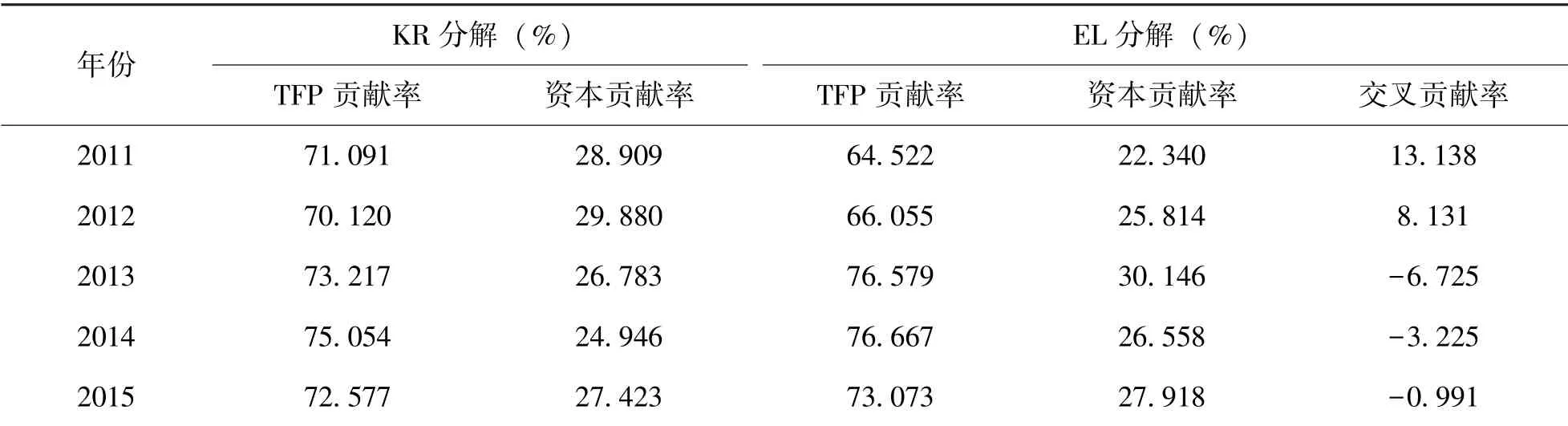
表2 2011～2017 年方差分解结果

续 表

2.2 收敛性分析

3.2.1 σ－收敛性

图1 与图2 分别展示了总体、 东中西以及东北部国家高新区劳均收入和TFP 对数值的标准差或σ－收敛性。 由图1 可知， 就标准差的变化趋势而言， 国家高新区总体劳均收入的标准差呈现出稳步下滑的态势， 年均下降0.062%， 说明总体国家高新区劳均收入具有σ－收敛趋势； 东部国家高新区劳均收入的标准差整体上呈现出了下降的态势， 年均下降0.078%， 具体而言， 由2011 年的0.380 下降至2017 年的0.333， 虽在2014 年出现了小幅上升(为0.377， 仍低于0.380）， 但随后呈现出了明显下降态势， 这说明东部国家高新区劳均收入也具有σ－收敛趋势； 中部高新区劳均收入的标准差呈现出了持续下滑态势， 年均下降1.80%， 具体而言， 在2014 年之前， 中部高新区劳均收入的标准差下降幅度较大， 2014 年之后，下降幅度则相对较小， 这说明中部高新区劳均收入也存在σ－收敛趋势； 西部高新区劳均收入的标准差整体上呈现出上升态势， 年均增长0.086%，具体而言， 除2014 年出现小幅下降外， 其他年份均出现了增长， 这说明西部高新区劳均收入呈现出发散趋势； 东北高新区劳均收入标准差的变动幅度较大， 尤其是2015 年和2016 年的标准差明显高于2011 年的标准差， 虽然在2017 年标准差出现了大幅下滑， 但2014 ～2017 年的标准差均值远远大于2011～2013 年的标准差均值， 这说明东北高新区劳均收入呈现出发散趋势。 进一步从劳均收入标准差数值大小分析， 东北部高新区标准差数值最大， 说明东北部高新区劳均收入的内部差距要大于东中西部高新区的内部差距； 中部高新区标准差数值最小， 说明中部高新区劳均收入的内部差距要小于东西以及东北部高新区的内部差距； 此外， 还可发现， 在2014 年之前， 东部高新区劳均收入的标准差高于西部高新区， 在2014年之后， 东部高新区的标准差低于西部高新区，这说明东部高新区劳均收入的内部差距在明显变小， 西部高新区内部差距在明显变大。

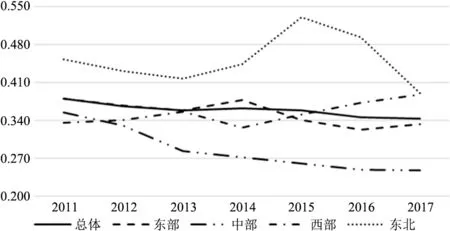
图1 总体、 东中西及东北部高新区劳均收入的标准差（σ－收敛性）

图2 反映了总体和分区域的国家高新区TFP标准差的变化态势。 由图2 可知， 从标准差的变化趋势而言， 总体国家高新区TFP 标准差呈现出平稳下滑的态势， 年均下降0.038%， 说明国家高新区总体TFP 存在σ－收敛趋势； 东部国家高新区TFP 的标准差整体上呈现出了下降的态势，年均下降0.065%， 具体而言， 由2011 年的0.291下降至2017 年的0.252， 虽在2013 年出现了小幅上升(为0.322）， 但随后呈现出了明显下降态势，这说明东部国家高新区TFP 也出现了σ－收敛趋势； 中部高新区TFP 的标准差呈现出了持续下滑态势， 年均下降1.40%， 这说明中部高新区TFP也存在σ－收敛趋势； 西部高新区TFP 的标准差整体呈现出上升态势， 年均增长0.08%， 具体而言，由2011 年的0.244 上升至2017 年的0.292， 除2012 年、 2014 年出现小幅下降外， 其他年份均是增长趋势， 这说明西部高新区TFP 呈现出发散趋势； 东北高新区TFP 的标准差的变动幅度较大，尤其是2014 ～2016 年标准差明显高于2011 年的标准差， 虽然在2017 年标准差出现了大幅下滑，但2014 ～2017 年的标准差均值远远大于2011 ～2013 年的标准差均值， 这说明东北高新区TFP 呈现出发散趋势。 进一步从TFP 标准差数值大小而言， 东北部高新区TFP 标准差的数值最大， 说明东北部高新区TFP 的内部差距要大于东中西部高新区的内部差距； 东部高新区TFP 标准差次之，说明东部高新区TFP 的内部差距要大于中西部高新区的内部差距； 中部高新区标准差数值最小，说明中部高新区TFP 的内部差距要小于东西以及东北部高新区的内部差距； 此外， 还可发现， 东中西部高新区TFP 标准差均值低于总体高新区均值，东北高新区TFP 标准差均值要明显高于总高新区均值， 这说明东北高新区TFP 的内部差距拉升了总体国家高新区TFP 的内部差距。

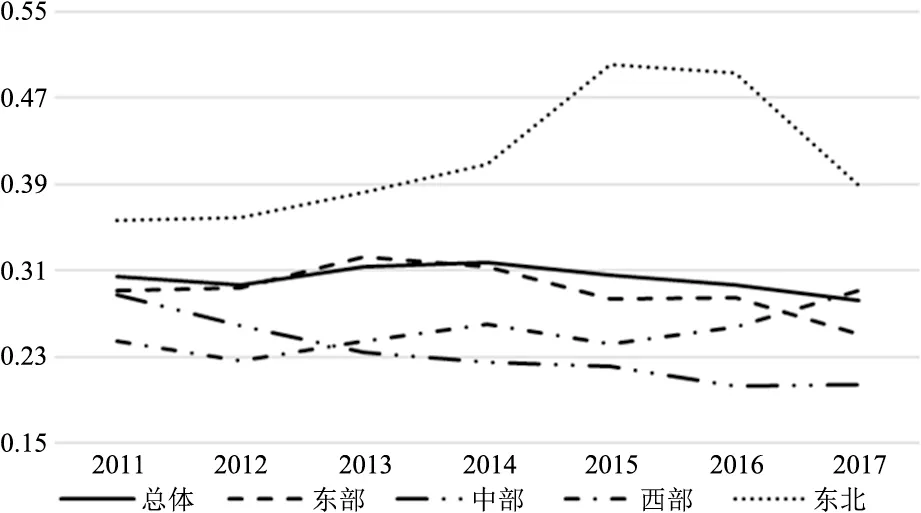
图2 总体、 东中西及东北部高新区TFP 的标准差（σ－收敛性）

通过对比劳均收入和TFP 标准差数值大小与演变趋势还可发现， 总体、 东中西部及东北国家高新区TFP 的标准差变化趋势与劳均收入标准差的变化趋势基本一致， 但劳均收入的标准差明显高于TFP 的标准差， 且劳均收入标准差增长或下降幅度均大于TFP 标准差增长或下降的幅度， TFP 区域差距与收入区域差距演变趋势的高度一致性也间接反映出两者间的互动关系。

2.2.2 绝对β－收敛

根据公式(9）～(11）， 我们采用OLS 回归对模型参数进行了估计， 参数估计结果如表3 所示。

表3 劳均收入和TFP 的绝对β－收敛（OLS 回归）

就总体高新区而言， βy的回归系数为－0.0639，且通过了1%的显著性检验， 总体高新区收入存在绝对β－收敛， 并以每年8.05%的收敛速度进行收敛； 东部高新区βy的回归系数为－0.0713， 且通过了1%的显著性检验， 东部高新区收入存在绝对β－收敛， 并以每年9.30%的收敛速度进行收敛， 出现了俱乐部收敛现象； 中部高新区βy的回归系数为－0.0965， 且通过了1%的显著性检验， 中部高新区收入存在绝对β－收敛， 并以每年14.41%的收敛速度进行收敛， 也出现了俱乐部收敛现象；西部和东北高新区βy的回归系数为负值， 但在统计上并不显著。 与前面的σ－收敛性分析结果一致， 总体、 东中部高新区收入均呈现出绝对收敛现象(σ－收敛也被称为绝对收敛）， 其中， 中部高新区收入的收敛速度最快， 东部高新区次之，总体高新区最慢。

总体高新区βTFP的回归系数为－0.0655， 且通过了1%的显著性检验， 总体高新区TFP 存在绝对β－收敛， 并以每年8.32%的收敛速度进行收敛； 东部高新区βTFP的回归系数为－0.0827， 且通过了1%的显著性检验， 东部高新区TFP 存在绝对β－收敛， 并以每年11.42%的收敛速度进行收敛； 中部高新区βTFP的回归系数为－0.0894， 且通过了5%的显著性检验， 中部高新区TFP 存在绝对β－收敛， 并以每年12.81%的收敛速度进行收敛； 西部和东北高新区βTFP的回归系数均为负值，但在统计上并不显著。 与前面的σ－收敛性分析结果一致， 总体、 东中部高新区TFP 均呈现出绝对收敛现象(σ－收敛也被称为绝对收敛）， 其中，中部高新区TFP 的收敛速度最快， 东部高新区次之， 总体高新区最慢。

从收入和TFP 的绝对β－收敛综合情况来看，中部高新区收入和TFP 收敛速度最快， 东部高新区次之， 总体高新区最慢。 进一步分析绝对收敛系数的大小可知， 总体、 东部高新区TFP 的收敛速度高于收入的收敛速度， 而中部高新区TFP 的收敛速度要低于收入的收敛速度。

2.2.3 条件β－收敛

根据式(12）～(14）， 我们采用Panel Data 固定效应(控制了截面固定效应和时间固定效应）对模型参数进行了估计， 估计结果如表4 所示。总体高新区βy的回归系数为－0.5362， 且通过了1%的显著性检验， 总体高新区收入存在条件β－收敛， 并以每年12.81%的收敛速度进行收敛；东部高新区βy的回归系数为－0.5037， 且通过了1%的显著性检验， 东部高新区收入存在条件β－收敛， 并以每年11.68%的收敛速度进行收敛；中部高新区βy的回归系数为－0.1766， 且通过了1%的显著性检验， 中部高新区收入存在条件β－收敛， 并以每年3.23%的收敛速度进行收敛； 西部和东北高新区βy的回归系数分别为－0.8426、－0.5289， 且均通过了1%的显著性检验， 并分别以每年30.82%、 12.55%的收敛速度进行收敛。

总体高新区βTFP的回归系数为－0.6328， 且通过了1%的显著性检验， 总体高新区TFP 存在条件β－收敛， 并以每年16.7%的收敛速度进行收敛； 东部高新区βTFP的回归系数为－0.6419， 且通过了1%的显著性检验， 东部高新区TFP 存在条件β－收敛， 并以每年17.11%的收敛速度进行收敛； 中部高新区βTFP的回归系数为－0.2136， 且通过了1%的显著性检验， 中部高新区TFP 存在条件β－收敛， 并以每年4%的收敛速度进行收敛； 西部和东北高新区βTFP的回归系数分别为－0.8456、－0.5676， 且均通过了1%的显著性检验， 并分别以每年31.14%、 13.97%的收敛速度进行收敛。最后， 通过比较收入与TFP 条件收敛的回归系数大小还可以发现， 总体、 东中西以及东北高新区TFP 的条件收敛速度要明显高于收入的收敛速度。

表4 劳均收入和TFP 的条件β－收敛（Panel Data 固定效应估计）

3 结论与启示

本文以2011～2017 年88 个国家高新区为研究对象， 采用方差分解和收敛分析方法探讨了TFP对国家高新区收入差距的决定作用并实证考察了TFP 的收敛情形， 研究发现： (1） 无论是KR 还是EL 分解， TFP 对国家高新区劳均收入差距的贡献远远大于资本投入的贡献， TFP 贡献约是资本贡献的2.5 倍。 具体而言， ER 分解结果显示， TFP 贡献为71.325%， 资本投入的贡献为28.675%； EL分解结果显示， TFP 贡献为70.575%， 资本投入的贡献为27.926%。 这说明TFP 而非资本投入是造成国家高新区经济发展差距的主要原因； (2）总体、 东中西部及东北国家高新区TFP 的标准差变化趋势与劳均收入标准差的变化趋势基本一致，但劳均收入的标准差明显高于TFP 的标准差， 且劳均收入标准差增长或下降幅度均大于TFP 标准差增长或下降的幅度； (3） 从收入和TFP 的绝对β－收敛情况来看， 总体、 东中部国家高新区存在绝对β－收敛现象。 从收敛速度来看， 中部国家高新区收入、 TFP 的绝对收敛速度最快， 东部高新区收入、 TFP 的绝对收敛速度次之， 总体高新区收入、 TFP 的绝对收敛速度最慢。 从四大区域的俱乐部收敛来看， 只有东部与中部国家高新区存在俱乐部收敛现象； (4） 从收入和TFP 的条件β－收敛情况来看， 总体、 东中西以及东北国家高新区收入和TFP 均存在显著的条件收敛。 其中， 总体国家高新区以每年12%以上的速度收敛， 东部国家高新区以每年11%以上的速度收敛， 中部国家高新区以每年3%以上的速度收敛， 西部与东北部国家高新区分别以每年30%以上、 12%以上的速度收敛。

基于上述研究结论， 我们可以得到以下启示：由于全要素生产率而非资本积累决定了高新区收入差距的主要部分， 单纯依靠资本积累不可能消除高新区之间的收入差距， 而缩小全要素生产率的差距才能有效解决国家高新区间收入差距问题，进而推动区域经济的协调发展。 具体而言， 各个国家高新区应充分结合自身实际， 因地制宜， 制定符合自身特色的发展战略。 对于全要素生产率水平较低的国家高新区而言， 要充分依托自身已有优势， 围绕产业链布局创新链， 加快借势借力，积极对接先进高新区的创新创业资源， 实现突破发展。 对于全要素生产率水平较高的国家高新区而言， 在不断提升发展质量和效益的同时， 应积极发挥对落后园区的引领和带动作用， 推动知识、技术、 人才、 资本向落后园区溢出， 进而促进不同国家高新区全要素生产率的均衡提升， 实现协同发展。

注释：

①国家高新区建设过程大致可划分为3 个阶段， 1991～2000 年为国家高新区一次创业阶段， 在这个阶段， 高新区建设的主要着眼点是聚集生产要素， 建设路经主要是打造园区开展生产的硬条件（如七通一平） 和招商引资， 建设的主要目标是快速形成产业基础和经济规模。 2001～2010 年为国家高新区二次创业阶段， 在这个阶段， 高新区核心强调的是要注入科技要素， 科技成果转化和技术创新应是高新区发展不能偏离的根本， 建设的主要目标更多转向于促进产业的价值链升级和以技术创新为本的内涵发展。2011 年后为国家高新区三次创业阶段， 在这一阶段， 国家高新区建设进入了“全面创新” 的时期。 从全面创新着眼， 高新区建设必须要着眼于一切有利于创新的要素， 建设路径必须致力于全面营造有利于创新的环境和开展自主创新， 这实际上就促使高新区开始向“创新经济生态” 的全面发展转型。