基于时间阈值的旅客登机模型及动态登机策略

任新惠，焦 阳，徐小冰

(1.中国民航大学经济与管理学院，天津300300；2.天津中科智能技术研究院，天津300300；3.长沙南方职业学院，长沙410000)

0 引 言

登机时间是旅客周转时间中的重要组成部分，据Nyquist 等[1]研究，航班周转时间每减少1 min就会节省约30美元.登机时间减少可以提高飞机的飞行次数，增加停机位服务飞机的数量[2]；对旅客来说，在登机口、廊桥或机舱过道等待时间缩短会使整个登机过程感知更加轻松[3].

登机问题的目标通常为登机时间最小，研究方法以仿真模拟和数学优化为主.Steffen[4]利用马尔可夫—蒙特卡洛优化算法提出Steffen 登机策略.Qiang 等[5]建立了座位吸引值模型和旅客选座行为模型研究自由登机策略.还有一些在已有策略基础上，从不同方面进行策略优化的研究.学者考虑到乘客放置行李过程是造成登机延误的关键因素[6-8]，从行李方面进行优化，任新惠等基于过道干扰转移思想提出了一种按行李数量安排座位的登机新策略[9]，建立多格子元胞自动机登机模型，提出了多行李优先登机策略[10].Milne 提出了一个将行李平均分布的座位预分配算法[6]；使用混合整数规划模型求解，根据旅客携带的行李数量分配座位[7]；Milne 等[11]运用两阶段混合整数规划模型分配旅客座位，进一步优化了登机过程.

以往研究多集中于提出新策略或对策略进行优化改进，但仍存在放置行李影响登机时间的情况，说明从行李方面还有进一步优化的空间.此外，以往登机时间模型通常用过道干扰和座位干扰的时间总和来代替登机时间，实际上，座位干扰可以分为有效座位干扰和无效座位干扰[12]，Kierzkowski等[8]通过统计5 000多位旅客的干扰情况得出，30%的座位干扰对总登机过程没有影响，故用干扰时间代替登机时间缺乏一定准确性.为完善登机时间模型，针对行李的影响探寻最优策略，本文提出干扰时间阈值的概念，运用数学模型和优化算法使所有旅客的过道干扰时间小于其对应的干扰时间阈值，并根据旅客携带行李数量不同，求解基于Steffen的动态登机策略.

1 模型构建

为便于问题讨论，登机问题的基本假设包括：以单通道客机经济舱为研究对象，机舱内20排，每侧3 个座位；旅客按照一定μs 的放行间隔和步速登机(其中μs 为时间步长单位)；过道只允许一名旅客同时通过；旅客到达指定座位所在过道放置行李；行李放置完成后进入座位，其座位元胞被占用，过道元胞变为空闲.

1.1 登机模型

为研究旅客过道干扰对登机时间的影响，将登机过程分为两个阶段，如图1所示.第1 阶段为旅客开始进入机舱时刻T0到预计最后一名入座旅客m进入机舱时刻Te_board结束.在这个阶段旅客陆续进入机舱，只有当机舱入口被占用时，后续旅客才会停止进入机舱，延长登机时间，这里将机舱入口占用时间称为入口延时td_door.

第2 阶段为预计最后一名入座旅客m进入机舱时刻Te_board开始到实际最后一名旅客入座的时刻Ta_board结束，在这个阶段尚未入座的旅客因为存在过道干扰，延长登机时间的部分称为入座延时td_seat.

图1 登机时间组成示意图Fig.1 Boarding time composition diagram

旅客登机时间可以分为无干扰登机时间、入口延时和入座延时3个部分，满足关系式

式中：tboarding为登机时间，即从第1名旅客进入机舱到全部旅客进入座位的时间；tuninterference为无干扰登机时间，指在没有任何干扰的情况下所有旅客全部入座的时间；td_door为入口延时；td_seat为入座延时.

考虑登机过程中延时问题的新登机模型相比前人模型更加直观便于理解，以下提出干扰阈值概念作为优化算法的基础.

1.2 入口延时

在第1阶段，机舱入口被占用是由于机舱内旅客的过道干扰时间超过干扰时间阈值，使后续旅客在机舱内拥堵到入口所致，因此入口延时满足关系式

式中：i为第1 阶段旅客；x表示座位的列；y表示座位的行；tinterference(i)为旅客i的过道干扰时间；Δt1(x,y,i)为第1阶段干扰时间阈值，该阈值只受到后续旅客到达r行的时刻Tr影响，即

如图2所示，以Steffen策略为例，旅客A4因为占用过道时间超过其时间阈值，造成机舱入口被占用，产生入口延时，干扰后续旅客进入机舱，延长了登机时间，而旅客A10 占用过道时间小于其时间阈值，不会延长登机时间.

图2 入口延时示意图Fig.2 Door delay diagram

1.3 入座延时

在第2 阶段尚未入座的旅客j的实际入座时刻Ta(j)超过预计最后一名入座旅客m入座时刻Te_board+te_board(m)时，将会延长无干扰登机时间tuninterference，产生入座延时td_seat，即

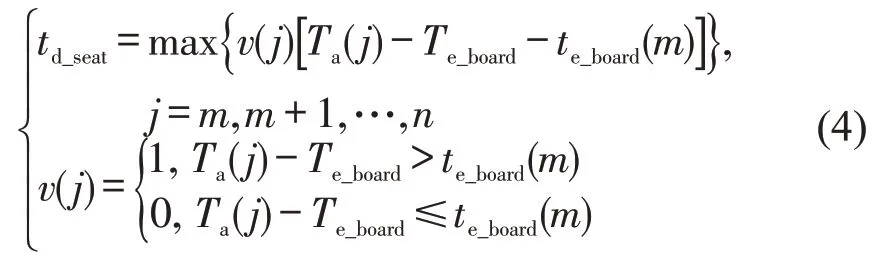
式中：j为第2 阶段未入座旅客；n为旅客数量；te_board(m)为预计最后一名旅客进入机舱到入座的预计时间；Ta(j)为旅客j的入座时刻，满足

式中：Tb(j)为旅客j进入机舱时刻；tinterference(j)为旅客j的过道干扰时间；te_board(j)为旅客j进入机舱到入座的预计时间.

将式(5)带入式(4)，得到tinterference(j)和td_seat的关系，即

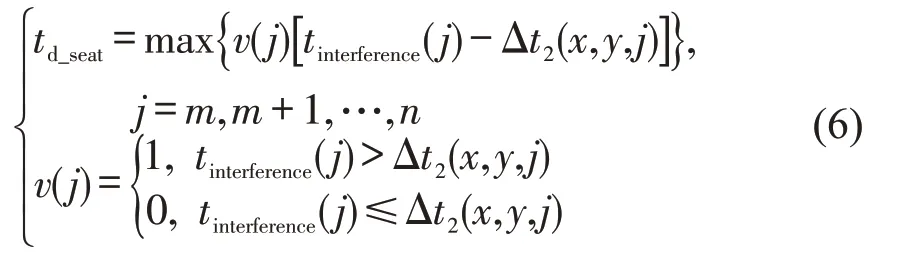
式中：Δt2(x,y,j)称为第2 阶段干扰时间阈值，且te_board属于无干扰登机时间的一部分，即

如图3所示，仍以Steffen 策略为例，旅客D19为预计最后一名入座旅客，旅客D19进入座位后，旅客D17、D15、D5仍占用过道，延长登机时间.

图3 入座延时示意图Fig.3 Seat delay diagram

图4展示了干扰时间与登机时间的关系.第1阶段的入口延时td_door和第2 阶段的入座延时td_seat组成登机延时.而第1 阶段和第2 阶段tinterference≤Δt(x,y)的旅客，虽然占用过道，但不延长无干扰登机时间，Δt(x,y)为第1阶段和第2阶段干扰时间阈值总称.

图4 干扰时间与登机时间关系示意图Fig.4 Diagram of relationship between interference time and boarding time

2 动态登机策略

Steffen 利用马尔可夫—蒙特卡洛优化算法提出Steffen 登机策略[4]，该策略完全避免了座位干扰，并且提高不同旅客在过道中处理行李的并行性，极大程度上减少了过道干扰.另外，通过真人登机实验可知，当旅客不携带行李时，按照Steffen次序登机能够完全避免座位干扰和过道干扰.因此，本节将基于Steffen登机策略，统计每个座位的干扰时间阈值；在此基础上研究行李分配的优化算法，指派每个座位行李的数量使过道干扰时间尽可能小于干扰时间阈值，使登机时间最小.

2.1 登机时间优化

建立新登机模型的目标是登机时间最小化，根据式(4)，优化模型为

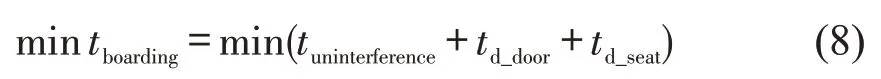
其中，无干扰登机时间在旅客数量、登机顺序和机舱结构固定的情况下，为常数项.因此优化模型变为

式(9)对过道干扰时间tinterference求导，得到

根据式(2)和式(6)，当过道干扰时间小于干扰时间阈值时，登机时间达到最小，即无干扰登机时间为

2.2 干扰时间阈值

在Steffen登机策略中，由前文分析可知，旅客D19 预计最后一个入座.旅客A20 到旅客C1 这前110 名旅客属于登机第1 阶段，在不造成入口占用的情况下，根据式(3)统计出第1 阶段干扰时间阈值Δt1(x,y,i).旅客D19到旅客D1后10名旅客属于登机第2阶段，根据式(7)统计得到第2阶段干扰时间阈值Δt2(x,y,j).通过仿真模型统计出Steffen 策略时120 个座位的干扰时间阈值分布，如图5所示，其中每一个座位上的数字为Δt(x,y)的值.仿真模型的参数设置为：放行间隔为1 μs ，x=A,B,…,F,y=1,2,…,20.

2.3 优化算法

在干扰时间阈值分布的基础上，通过优化算法分配行李，使得过道干扰时间与干扰阈值之间的差值最小，最大程度地减少放置行李对登机时间的影响.优化算法的具体步骤如下：

Step 1按照多件行李优先的原则，将行李从多到少排列，并设置行李架上的初始行李数量nbin(x,y)=0,x=A,B,…,F,y=1,2,…,20.

Step 2参考机舱干扰时间阈值分布，遍历寻找min[tinterference(x,y,i)-Δt(x,y,i)]的位置，确定携带行李旅客所在的座位.

Step 3重复Step 2，依次确定所有行李的位置.

Step 4确定120 个座位上的行李数量，为证明在不同的行李数量分布下优化算法得到的结果都为最优策略，选取0，1，2件行李数量比例分别为43∶52∶25和12∶72∶36两种行李数量分布，由优化算法分别得到行李分配的优化算法结果，如图6所示，图中每个座位上的数字为该位置摆放行李的件数.

图5 Steffen 策略干扰时间阈值分布Fig.5 Interference time threshold distribution of Steffen strategy

图6 Steffen 策略行李分配优化结果Fig.6 Baggage allocation optimization results of Steffen strategy

所提出的动态登机策略实质上是从两个方面组织登机过程：一方面，根据旅客携带行李数量进行座位分配，如图6所示，携带不同数量行李的旅客被分配到不同的座位，使得每个座位上放置行李时间尽可能低于时间阈值；另一方面，在登机次序上按照Steffen 的序列登机，能够在登机过程中减少干扰.根据实际情况中，旅客携带行李数量的不同，优化算法会求解出不同的行李分配结果，故该策略是动态变化的.

3 实验与结果分析

为验证新登机模型的正确性和动态登机策略的效率，使用元胞自动机仿真实验和真人现场模拟实验两种方法进行验证.元胞自动机仿真实验以经典单通道机舱为例，设计为20行6列，放行间隔为1 μs，仿真通过Matlab2012B编程实现.

3.1 仿真实验结果分析

通过设置不同的行李比例，仿真运行BF_3、BF_4、Random、OI、RP_4 和Steffen 这6 种登机策略，统计4 种行李情况下新登机模型的时间组成：登机时间tboarding、无干扰登机时间tuninterference、入口延时td_door、入座延时td_seat，统计结果如图7所示.

图7 登机模型的时间组成Fig.7 Time composition of boarding model

从图7中可得到以下结论，登机时间的3个组成部分无干扰登机时间、入口延时、入座延时与登机时间的关系满足登机模型，即式(1).由图7(a)可知，当旅客不携带行李时，BF_3、BF_4、Random 这3种策略登机过程中不存在行李干扰时间，但仍存在座位干扰，且座位干扰会产生入口延时和入座延时，导致登机时间比无干扰登机时间长.而OI、RP_4 和Steffen 这3 种策略避免了座位干扰，因此登机时间和无干扰登机时间一致；由图7可知，随着旅客携带行李的增多，机舱内旅客的过道干扰时间增加，产生入口延时和入座延时，使得登机时间都有所增加；对比不同行李比例下的6种策略可知，Steffen策略表现得更高效、更稳健.

为使本文的优化算法与前人的研究具有可比性，将优化算法与经典Steffen 策略和基于Steffen的两种改进策略[6]在同一个元胞自动机仿真环境中进行实验对比.选取文献中一种行李比例，即0，1，2件所占比例为43∶52∶25，得到4种策略的登机时间构成情况如图8所示.仿真结果显示：经典Steffen策略的登机时间为185 μs，登机次序使旅客在机舱内避免了座位干扰，但放置携带行李会产生入口延时和入座延时；基于Steffen的两种改进策略通过分配行李再登机，登机时间分别为159 μs 和176 μs，相对于经典Steffen减少了登机时间，这两种策略虽然将入口延时和入座延时时间缩短，但仍存在延时；本文通过优化算法分配行李将行李放置时间控制在干扰时间阈值以内，有效地避免了入口延时和入座延时，使登机时间缩短为129 μs，使得登机时间与无干扰登机时间一致；本文的优化结果相比于经典Steffen，效率提高30.27%；相比于文献[6]和文献[7]的优化进一步优化了18.87%和9.66%.

图8 优化算法验证Fig.8 Optimization algorithm verification

改变旅客携带行李数量为0，1，2 件比例为12∶72∶36 时，本文的动态策略用时154 μs ，Milne 2016年的改进策略用时194 μs.结果表明，当行李数量增加时，动态策略的行李分配发生变化，并且相比2016年的改进策略效率提高了20.62%.可见动态登机策略具有比之前的策略进一步优化了时间且具有一定的稳定性.

3.2 现场模拟实验结果分析

本文选取Random、BF、OI、RP、Steffen 和动态登机策略6种策略，组织144名参与者在48座飞机模拟舱中进行了3～4 次登机实验.首先，选择Steffen策略和本文的动态登机策略来验证新登机模型；其次，将它们与Random策略进行比较，以评估动态策略的性能.

根据前文图3对登机阶段的分析，当登机总人数为48 时，乘客D7 为预计最后一名乘客，作为两阶段的分界点.与不携带行李时的Steffen相比，通过观察实验视频，可以获得入口延时和入座延时，如表2所示.当旅客不携带行李并运用Steffen次序登机时没有产生座位或过道干扰，故其登机时间被视为无干扰登机时间，即136 s.新登机模型的无干扰登机时间、入口延时、入座延时3 个组成部分的总和是173 s和149 s，而仿真模拟实验的登机时间是183 s 和152 s，偏差为5.50%和2%.由于实验视频观测中的最小单位是秒，并且统计中存在一定的主观误差，故可以认为新登机模型是准确的.

表1 登机模型验证Table1 Boarding model verification (s)

登机时间是评估登机效率的重要指标，真人模拟实验得到Random、BF、OI、RP、Steffen 和动态策略6 种策略的登机时间分别为：269，279，206，191，183，152 s.可以看出，登机动态策略的登机时间最短，相比于传统Random 和BF 策略登机效率提高了43%和46%.另一方面，通过组织模拟实验也表明，动态策略在实际登机中具有可行性和可操作性.

4 结 论

针对以往登机时间模型用干扰时间代替登机时间存在的重复统计或遗漏的情况，本文将登机过程分成两个阶段，建立了新登机模型，在干扰时间阈值的基础上运用优化算法求解出行李分配结果，并得到登机动态策略.主要结论如下：元胞自动机仿真实验验证了新登机模型的正确性；仿真结果表明：当行李比例，即0，1，2 件所占比例为43∶52∶25时，动态登机策略相比于经典Steffen策略，登机时间效率提高30.27%；当行李数量增加，即0，1，2 件所占比例为12∶72∶36 时登机时间效率提高20.62%；组织现场模拟实验结果表明动态策略在实际中具有可行性，并且相比于Random和BF效率提高43%和46%.

由于动态登机策略在实施过程中需要在登机前知道旅客携带行李件数，因此，未来可在值机或安检系统中加入收集旅客携带行李的步骤，不仅有利于提高登机效率，而且便于旅客行李管理.无论是手机值机、自助值机，在相应值机系统中增加填报行李数量的选项；这样登机系统就可以根据旅客填报行李数量进行座位的分配.如果旅客要进行自主选座，可根据行李分配的结果对座位进行锁定，旅客只能选择符合行李数量的座位.目前实施的“付费选座”“会员选择”等，航空公司可结合已分配行李数量的座位综合考虑，即满足登机效率的要求，又满足旅客服务、效益的需求.这个问题还有待进一步深入研究，寻求效率、效益的最佳结合点.本文提出的干扰阈值概念可以运用到按照预先指定的次序进行登机/入座/进场等其他领域.旅客行走速度、放行间隔和携带行李的多少都会影响旅客入座时间，因此，如何将两个阶段更明显地划分，以及如何确定最后一名入座旅客都将是进一步研究的内容.