带时间窗的多行程交换箱甩挂路径优化
彭 勇,高 鹤
(重庆交通大学交通运输学院,重庆400074)
0 引 言
带交换箱的甩挂运输(Swap-body Vehicle Routing Problem,SB-VRP)由于具有对不同道路条件的灵活性、提高运输效率、减少运输成本的潜力而受到企业与学者关注.该问题可以看作是卡车和拖车路线问题(TTRP)的一个变体[1].本文研究的小型交换箱甩挂运输车可以由一节交换箱组成的卡车去服务通行道路有限制(道路条件不允许较大车辆通行)的限制客户点(限制点),也可以由带两节交换箱组成的整车去服务通行道路没有限制(道路条件允许较大型车辆通行)的灵活客户点(灵活点),交换箱可临时存放于甩挂点.
在配送实践中,客户往往会要求在特定的时间窗内为其提供配送服务,使带时间窗的路径优化成为学者关注的内容.大量学者开始研究VRPTW[2-3].另一方面,现实物流配送中,司机完成一次配送任务后可能距离下班还有一段时间,为充分利用司机日常工作时间,可安排新的配送任务(多行程)实现进一步的成本节约[4].关于带时间窗的多行程路径优化问题,国内外研究较少[5-7].
随着甩挂运输的兴起,学者开始注意到将甩挂或交换箱应用到物流配送领域可带来配送效率的提升.边展用两阶段启发式算法研究带时间窗的甩挂运输路径优化,对整车的实际配送有一定的使用价值[8].Túlio A.M.提出了启发式的随机局部搜索算法来研究SB-VRP[9].但已有的SB-VRP研究尚未同时考虑实际配送中可能存在客户时间窗要求且企业允许多行程配送情况,本文将研究时间窗约束下多行程SB-VRP路径优化问题.
1 模型构建
1.1 问题假设与符号说明
问题假设:
(1)限制点只能由卡车服务,灵活点既可以卡车服务也可以用整车服务.
(2)每辆车每个任务的始发与结束都是在配送中心.
(3)本研究为小型交换箱,用于城市物流配送,通常单个客户的需求量相对较小,假设每个客户点被配送一次,同时要满足每个客户点的需求量.
(4)任一配送路线上客户点的总需求量不超过所用运输车最大允许载荷.
(5)每辆车的总工作时间不超过司机的单日工作时间.
(6)每辆车到达客户点的时刻就是开始服务的时刻.
(7)不考虑道路拥堵及时变情况,车辆的平均行驶速度均相同.
图1为车辆示意图,图2为SB-VRP 配送路径的示意图.
令有向网络图G=[N,A],其中,N表示所有节点的集合,N=Ns+Nr+Nf+{0},Ns表示甩挂点集合,Nr表示限制点集合,Nf表示灵活点集合,0代表配送中心,A为从客户点i到客户点j的边集,A={(i,j):i,j∈N,i≠j}.K为卡车集合,E为交换箱拖车集合,R为行程集合.

图1 卡车与整车示意图Fig.1 Truck and complete vehicle schematics

图2 不同车辆的运输路线图Fig.2 Transport road map for different vehicles
(1)符号与集合.
i,j——节点,i,j∈N;
k——卡车,k∈K;
e——交换箱拖车,e∈E;
r——行程,r∈R.
(2)参 数.
Cij——卡车从i点到j点的行驶时间;
bk,be——卡车、交换箱拖车行驶单位里程所需费用;
ck,ce——卡车、交换箱拖车的使用费用;
f——雇佣司机的费用;
Qk,Qe——卡车、交换箱拖车的额定装载量;
qi——节点i的需求量;
Fdelay——车辆晚于客户时间窗所产生的单位时间惩罚成本;
——节点i时间窗的上限;
——车辆到达节点i的时刻;
——车辆在i点的服务时间;
h——司机在1 d 允许工作的最长时间(h);
v——车辆的平均速度;
σ——晚于时间窗60 min以后的惩罚系数.
(3)变 量.
——0-1 变量,当边(i,j)之间有直接路径且属于k的第r次行程时,1,否则0,∀i,j∈N,∀k∈K,r∈R;
——0-1 变量,当边(i,j)之间有直接路径且属于k的第r次行程时,1,否则0,∀i,j∈N,∀e∈E,r∈R;
yk——0-1变量,卡车k被选中时,yk=1,否则yk=0;
ye——0-1变量,卡车e被选中时,ye=1,否则ye=0.
1.2 模型建立
目标函数为
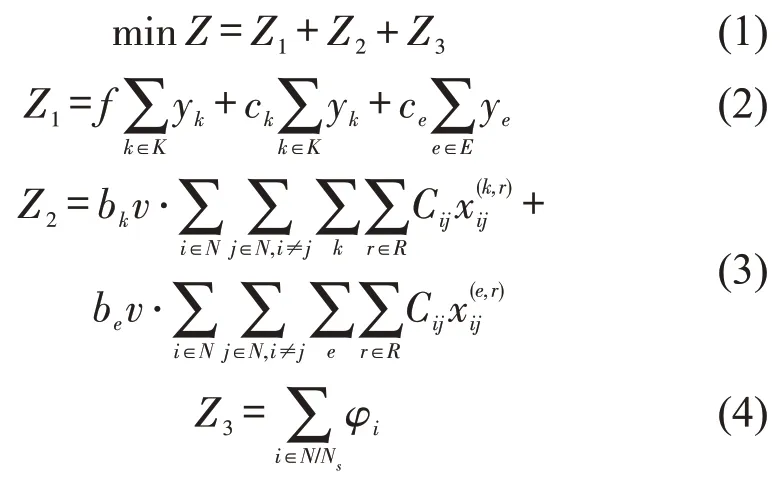
约束条件为
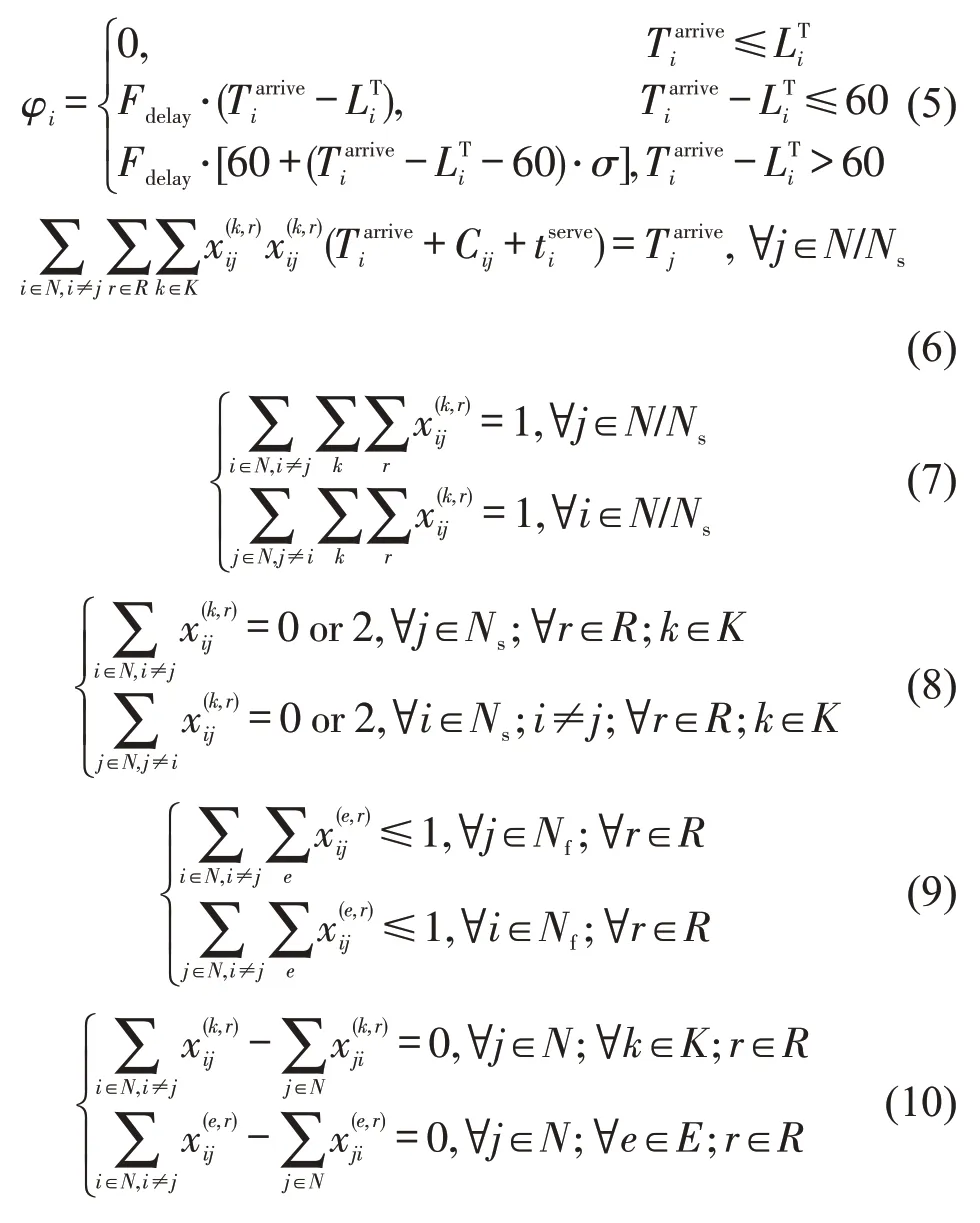

式(1)为最小化整个配送过程中的成本,包括车辆派遣成本Z1、运输成本Z2和时间惩罚成本Z3.式(2)为车辆派遣成本,包括卡车和交换箱拖车的启动费用及司机工作费用.式(3)为运输成本,包括卡车和整车运输费用.式(4)为时间惩罚成本,即车辆到达客户点的时刻晚于客户时间窗上限会有不同的惩罚成本.式(5)为晚于客户时间窗的惩罚成本.式(6)为车辆到达客户点j的时间约束.式(7)为路网中任意客户点(不包括甩挂点)有且仅有一条行程为一次的卡车服务路线.式(8)为该路径是否为允许甩挂的路径,若是仅有一次甩挂操作.式(9)为路网中经过灵活点的交换箱拖车连线最多为1,也可能不存在.式(10)为车辆进出节点的平衡约束.式(11)为车辆每次行程最多能从配送中心出发一次.式(12)为路径中交换箱拖车取值不大于1,卡车一定为1.式(13)为车辆载重约束.式(14)为卡车完成r次行程的总时间不得超过司机每日工作的最长时间.
2 算法设计
遗传算法作为一种常用的全局优化算法,在求解路径优化问题上具有较好的效果,故在传统遗传算法的基础上提出基于装箱算法和时间窗局部优化策略的混合启发式遗传算法,对本文提出的问题进行求解.
2.1 编 码
采用随机小数编码[10].假设一条路径允许形成最多的任务数为ζ,限制点个数Nr,灵活点个数Nf,则染色体长度为(Nr+Nf+ζ-1).假设有11个客户(包含5 个限制点客户和6 个灵活点客户),最多有4 个配送任务,则染色体长度为11+4-1=14.以图3给出的小数编码为例,长度为14的小数向量表示一条染色体.
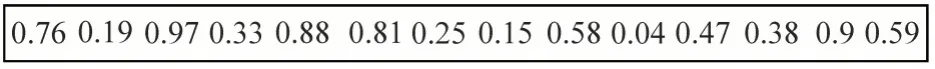
图3 小数编码示意图Fig.3 Decimal coding schematic diagram
2.2 解 码
(1)解码产生初始路径.
按升序规则,将对应基因位的小数用顺序号代替,将上述小数编码映射为1到(Nr+Nf+ζ-1)的整数排列[11].令限制点的编号为1~Nr,灵活点的编号为Nr+1~Nr+Nf,分隔符编号为Nr+Nf+1~Nr+Nf+ζ-1.分隔符的作用在于将整条体染色体进行分割,分割之后的每一小段染色体都代表一条完整的配送路径.以图3为例,图4给出了一个产生初始路径的实例,规定小数排列的后三位为分隔符即12、13、14,对应路径如图5所示.

图4 初始路径Fig.4 Initial path

图5 初始路径示意图Fig.5 Initial path diagram
(2)客户配送顺序的优化.
对于路径中既有限制点又有灵活点,且配送总量超过卡车容量却小于带交换箱的整车容量,采取限制点优先配送的方案,得出优先配送限制点的路径调整及路径示意图如图6和图7所示,在图中1~5为限制点.

图6 客户顺序优化路径调整Fig.6 Customer order optimization path adjustment

图7 客户顺序优化路径示意图Fig.7 Customer order optimization path diagram
(3)考虑车辆载重限制的优化.
有甩挂操作的路径中:首先,判断配送任务中限制点总需求量是否超出Qk,将超出Qk的限制客户点从该配送任务中拿出;然后,再将整个配送任务中超出Qk+Qe的灵活客户点拿出;最后,找出限制点需求加起来小于Qk的任务,将上一步取出的限制点放入,对待灵活点同理,如果没有符合要求的任务,则开启一个新任务将其放入.考虑车辆载重限制的路径调整及路径示意图如图8和图9所示,图中数字分别代表不同的客户,1 为超出Qk的客户点,6为超出Qk+Qe的客户点.

图8 车辆载重优化路径调整Fig.8 Vehicle load optimization path adjustment.

图9 车辆载重优化路径示意图Fig.9 Diagram of vehicle load optimization path
(4)添加甩挂点.
对于既有限制点又有灵活点,且配送总量超过卡车容量却小于带交换箱的整车容量的路径,在以上调整后,启用距离第一个限制点最近的甩挂点作为该路径的甩挂点.整车从配送中心出发到甩挂点将第二个交换箱放下,变成卡车去服务限制客户点,完成配送后回到甩挂点拖带上交换箱,形成整车继续为灵活客户点服务,路径调整及车辆行驶路径示意图如图10和图11所示,图中15代表甩挂点.

图10 添加甩挂点路径调整Fig.10 Add swing point path adjustment

图11 添加甩挂点路径示意图Fig.11 Path diagram of adding swing point path
(5)任务安排策略.
为最大化利用司机的工作时间,采用一维装箱算法对司机进行多配送任务指派.将司机1 d的工作时长看作是一个箱子容量,某司机在完成一个配送任务后返回配送中心的时刻距离下班时刻的这段时间,相当于装箱后箱内剩余容积.每个配送任务的总时间就相当于一件物品,将该物品放入箱中后,若该箱子还可以容纳其他的物品,则将其他物品装入该箱子,以此类推,但规定每个箱子最多装3 个物品.2 个或3 个物品装入一个箱子代表一个司机在1 d的工作时间内要完成2个或3个配送任务.多行程安排及配送路径优化示意图如图12和图13所示.

图12 任务安排策略路径调整Fig.12 Task scheduling policy path adjustment

图13 任务安排策略路径示意图Fig.13 Task scheduling policy path diagram
(6)时间窗局部优化策略.
既要提高客户满意度,又要保证运输成本最小;同时配送车辆到达客户点的时刻不得超过客户时间窗太久,否则会受到相当大的惩罚成本.因此,在图2~图9中采用时间窗局部优化策略对路径中客户的时间窗进行排序.在不改变单个配送任务中需要配送的客户点的基础上,对时间窗较早的客户点先配送.对应添加甩挂点的配送路径,对限制点和灵活点的时间窗分别调整.时间窗局部优化策略路径调整及配送路径优化如图14和图15所示.

图14 时间窗局部优化策略路径调整Fig.14 Local optimization strategy path adjustment of time window

图15 时间窗局部优化策略路径示意图Fig.15 Schematic diagram of local optimization strategy path for time window
2.3 遗传操作
选用轮盘赌进行个体选择,选中概率与个体适应度呈正相关,被选中的个体随机配对;采用二进制单点交叉操作,将交叉点之前或之后的部分互换;使遗传算法具备局部随机搜索能力且维持群体多样性,有效预防早熟收敛现象的产生.本文既要保留优秀个体又要防止过早收敛采用单点变异操作.
3 数值实验
3.1 算例描述
采用MATLAB2014b 编程,在一台CPU 型号为Intel Core I5-8265U、8 G内存、64位操作系统的计算机上运行.
采用Solomon标准实例数据集R101数据生成案例,如图16所示,为验证模型与算法的可靠性,增加多个数据集进行算例分析.将配送中心定为第121 个坐标点,依次选择坐标点111~120 为甩挂点,坐标点1~40为灵活客户点,坐标点41~90为限制客户点.令卡车与带交换箱的整车的最大装载量分别为200和400,车辆平均行驶速度为1,卡车与交换箱的启用成本均为1,单位行驶成本为1,带交换箱的整车的单位行驶成本为1.5,甩挂点的启用成本为5,司机日常允许的最长工作时间为8 h,单日薪资为10,时间窗调整为原数据的2.4 倍.时间惩罚成本呈折线型,单位时间的惩罚成本为0.8,晚于时间窗60 min后的惩罚系数为1.5.
3.2 有效性实验
为验证算法的有效性,初始种群的规模N=100,交叉概率Pc=0.9,变异概率Pm=0.4,最大迭代次数M=1 000.从图17中看出,在迭代次数为450 次左右时,得到最优解并进入收敛状态.算法连续运行10 次得到最优解如表1所示,结果偏差为9.1%,在可以接受的范围(15%).10 次最好解配送路径如图18所示.为更好地验证算法的可靠性和适用性,增加多个数据集的对比实验,实验结果如表2所示.实验结果表明,该算法针对所提出的问题,求解质量和稳定性都较好.
3.3 多行程策略有效性分析
在M=500,N=100 时,对比是否允许采用多行程策略的最优配送路径与迭代收敛图,如图19所示.采用多行程策略运输路径的最小总配送成本较小,启用的车辆数目也会减少.从表3清晰地看出,运输车辆采取多行程策略与未采取多行程策略得到的最优路径的平均运输成本分别为1 562.3和3 295.5.结果说明,多行程策略对路径优化及司机工作时间的利用率影响明显.
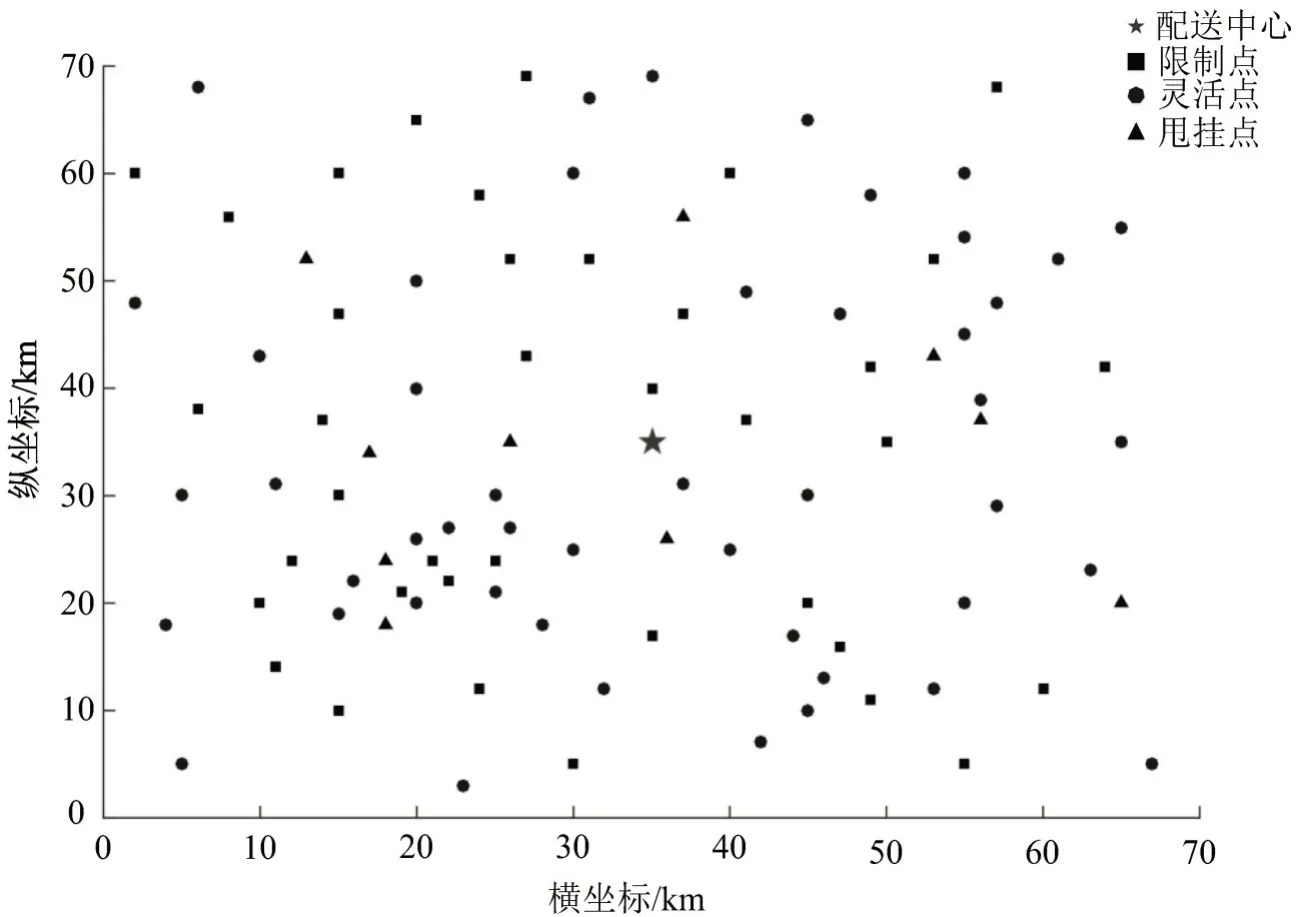
图16 R101 实验数据点分布图Fig.16 Distribution of experimental data points

图17 迭代收敛图Fig.17 Iterative conver gence diagram

图18 最优配送路径图Fig.18 Optimal distribution path diagram
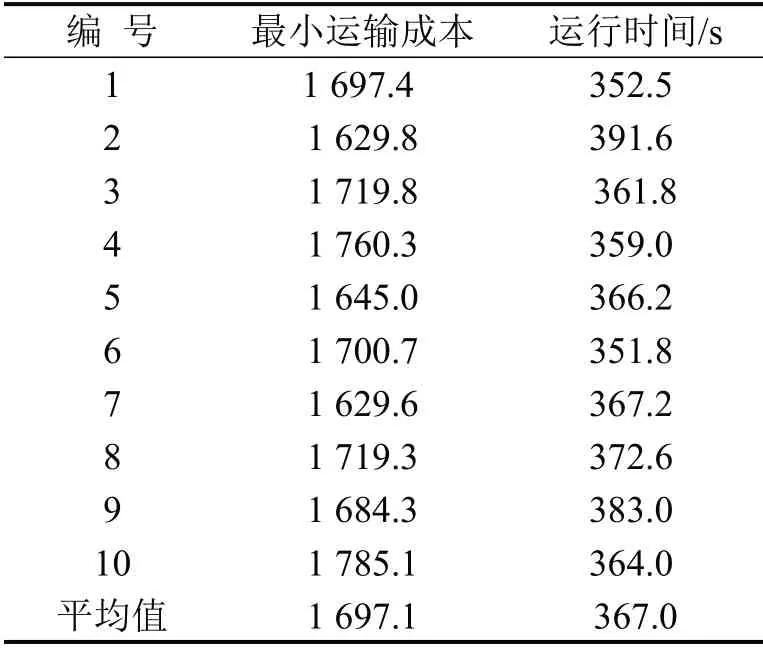
表1 求解最优解结果Table1 Results of solving optimal solution

表2 不同数据集对比结果Table2 Comparison results of different data sets

图19 有无多行程策略对比图Fig.19 Comparison of multi-trip strategies
3.4 根据客户时间调整策略有效性分析
如表4和图20所示,对比是否采用客户时间窗调整策略的最优配送路径与迭代收敛图可以看出,算法中采用客户时间窗调整策略后,在满足时间窗的客户点数量、最小运输成本、运输途中的总延误时间这3个方面,都比不采用客户时间窗调整策略算法得到的结果好.

表3 多行程策略结果Table3 Results of multi-stroke strategy

表4 客户时间窗调整对比结果Table4 Comparative results of customer time window adjustment

图20 客户时间窗调整最优解对比图Fig.20 Comparison diagram of optimal solution for customer time window adjustment
3.5 时间惩罚系数灵敏度分析
对比分析不同时间惩罚系数得出,惩罚系数对最小运输成本及最优运输路径均有影响,如图21和图22所示.在现实生活中,不同客户对时间窗需求的严格程度不同,可通过调整时间惩罚因子对路径安排进行调整,在客户满意与运输成本间寻求平衡.
4 结 论
在城市及近郊的物流配送环境背景下,研究带时间窗的多行程SB-VRP 问题.为解决该问题,设计了基于遗传算法和装箱算法的混合启发式算法,并结合时间窗、多行程等约束条件进行数学建模,使用经典的Solomn数据集进行数值实验,验证所提算法具有较高的可行性和实用价值.

图21 不同时间惩罚系数对比图Fig.21 Comparison diagram of different time penalty factors
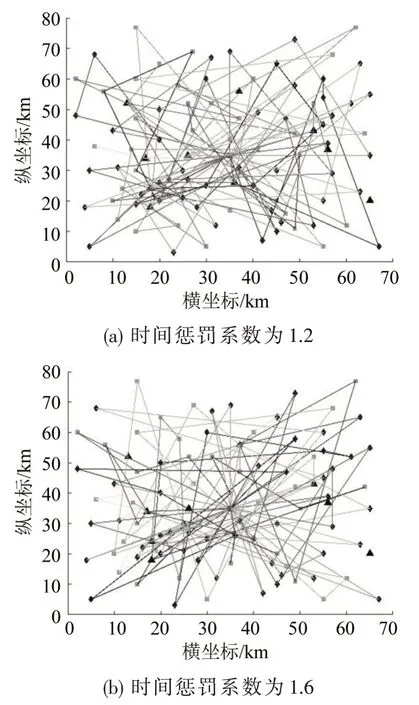
图22 不同时间惩罚系数的路径图Fig.22 Path diagram of different time penalty coefficients
由于实际路径的时间很大程度是受交通流影响的,影响因素有很多种,如时变、拥堵、交通事故、天气原因等,将这些因素考虑在内的话,优化过程会比较复杂,后续可以继续深入研究.同时求解路径优化的算法有很多种,比如蚁群算法、神经网络、局部搜索等,本文采用的遗传算法是较为经典与传统的,后续研究可以进行多种方法对比与改进.

