直达链路下的多用户分集与全双工中继系统

徐伟， 赵睿

(华侨大学 厦门市移动多媒体通信重点实验室， 福建 厦门 361021)

射频信号能同时携带信息和能量，为充分利用射频信号，学者们对同步无线信息和功率传输(SWIPT)进行了广泛地研究[1-4].Nasir等[5]分析放大转发传输系统，在低信噪比和高传输速率下，得到时间切换中继协议在吞吐量方面优于功率分配中继协议的结论.在此基础上，Nasir等[6]进一步研究解码转发中继系统的吞吐量性能.Zhao等[7]为最大化系统吞吐量求得最佳时间切换因子.Ikhlef等[8]分析多中继网络中的中继选择问题.相较于无电池中继，带电池中继在提升系统性能方面具有更大的优势.Song等[9]利用拉格朗日乘法获得最佳发射功率的闭合表达式，提出的联合最优功率分配和中继选择策略可以在能量采集和全双工信息传输两个阶段中获得源节点的不同发射功率.Do[10]提出一种基于混合功率时间分配的中继协议，分析最佳时间切换和最佳功率分配系数对吞吐量的影响.Ojo等[11]分析系统吞吐量随中继节点采集能量的变化情况，结果表明，所提协议优于基于时间切换和基于功率分配的中继协议.Lee等[12]在高信噪比条件下，推导出系统中断概率和最佳功率分配因子.Mahama等[13]利用最大比合并技术将直达链路信号和中继信号合并，在延迟受限传输模式下，针对具有能量采集的中继网络，推导出中断概率的闭合表达式，揭示具有直接链路的中继网络的优势.Zhao等[14]研究时间切换中继协议，分析源传输速率、源到中继的距离和噪声功率对吞吐量的影响，并与文献[13]进行比较.综上可知，相关研究涉及多目的地情境下，源与每个目的地之间存在直达链路、中继工作在全双工模式下的多用户分集问题.因此，本文针对多目的地传输网络，提出基于时间切换协议的全双工协作中继方案.

1 系统模型和信息传输

1.1 系统模型的传输结构

系统模型是1个协作中继传输网络，由1个源节点(S)、1个全双工中继节点(R)和K个目的用户节点(D1，…，Dk，…，DK)构成，源节点和目的用户节点都是单根天线，中继节点配备NR根天线.

对系统模型做以下3点假设.

1) 所有信道均为瑞利衰落信道且相互独立，服从指数分布.

2)hi，j，di，j分别为节点i，j之间的信道参数和距离；m为路径损耗指数；λi，j为节点i，j之间的平均信道增益；ni为节点i接收到的均值为0，方差为N0的加性高斯白噪声(i，j={S，R，D1，…，DK}).

3) 该放大转发协作网络受总功率约束，即PS1+PS2=PS，PS表示整个时间块T内源节点的总发送功率.设PS1=βPS，PS2=(1-β)PS，0<β<1,β为源功率分配比.

系统模型及传输结构示意图，如图1，2所示.由图2可知：T被时间切换比α分为两个不同的时隙.在第一时隙αT内，S利用发送功率PS1,将其归一化能量符号xE发送到中继R，同时，R进行能量采集；在第二时隙(1-α)T内，S利用发送功率PS2,将其归一化信息符号xI发送给中继R和目的节点Dk，同时，中继R发送信息xR到目的地Dk.

图1 系统模型 图2 传输结构示意图 Fig.1 System model Fig.2 Illustration of transmission structure

1.2 中继链路传输

在全双工系统中，自干扰是客观存在的，且自干扰也可以被抑制到噪声水平[15-16].为了最小化自干扰，中继同时选择接收和发送天线，则有

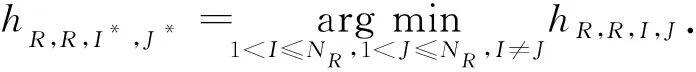
(1)

式(1)中:I表示第I根信息接收天线;J表示第J根信息发送天线；I*表示自干扰最小时被选中的信息接收天线；J*表示自干扰最小时被选中的信息发送天线.

该方法相当于从NR(NR-1)/2个信道中选择自干扰最小的信道.当中继天线数NR趋于无穷大时，自干扰信道的信道增益等价于常数ε，即

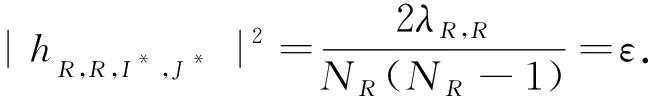
(2)

在第一时隙αT内，中继节点收到的信息yS，R1为

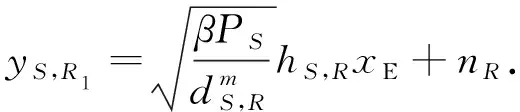
(3)

式(3)中:E[|xE|2]=1，E[X]表示对X求均值，|·|为绝对值运算符.

因此，第一时隙αT内中继采集的能量Eh为

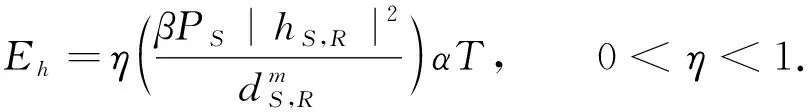
(4)

式(4)中:η为能量采集效率.

因此，在第二时隙(1-α)T内，中继的发送功率PR为

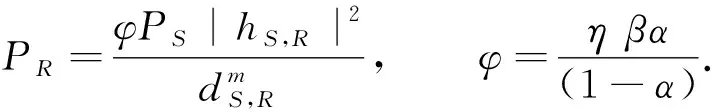
(5)

在第二时隙(1-α)T内，中继接收的信息yS，R2为

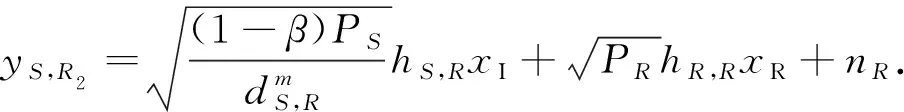
(6)

式(6)中:E[|xI|2]=1；E[|xR|2]=1，xR=GyS，R2，G为放大转发因子.

中继R采用放大转发协议，其放大转发因子G为

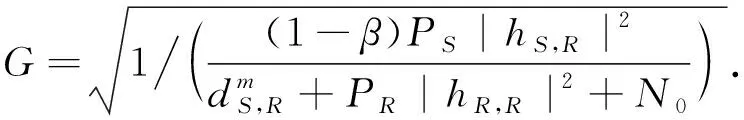
(7)

在第二时隙(1-α)T内，S通过中继转发信息到已选择的目的地Dk，接收的信息yDk,1为

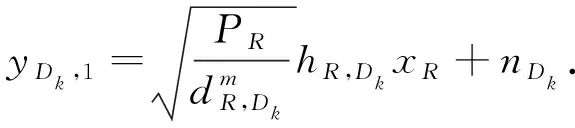
(8)

此时,目的地Dk的接收信噪比γDk,1和累积分布函数FγDk,1(v)分别为

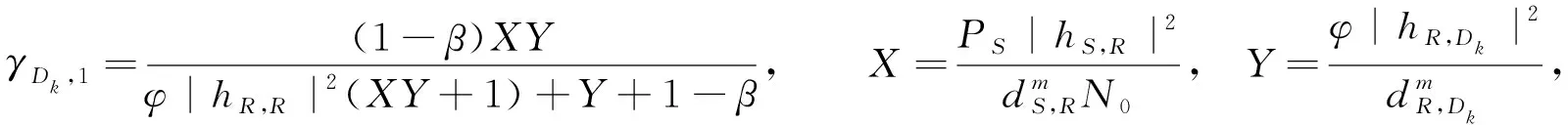
(9)

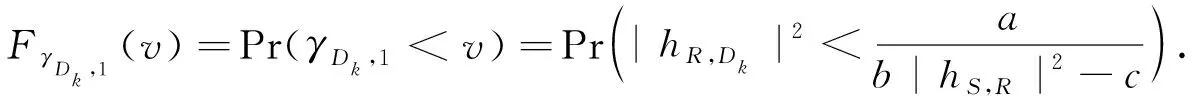
(10)

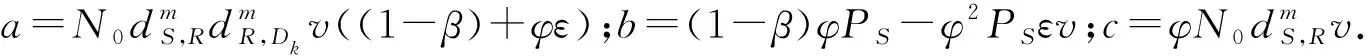
已知|hS，R|2和|hR,Dk|2是两个相互独立且服从指数分布的随机变量，则式(10)可写为

(11)

因此，式(11)可表示为

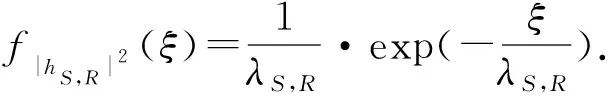
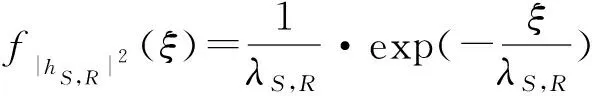
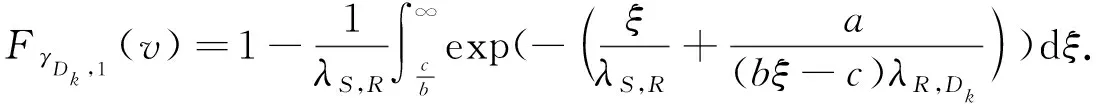
(13)

定义1个新的积分变量δ=bξ-c，因此，累积分布函数FγDk,1(v)可表示为

(14)

最后，通过文献[17]中的式(3.324.1)，使累积分布函数FγDk,1(v)简化为

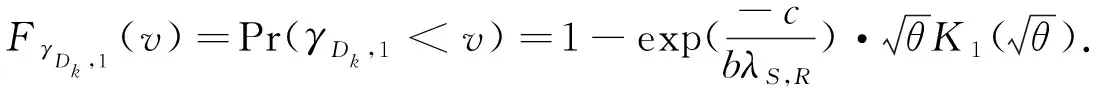
(15)

1.3 直达链路传输

在第二时隙(1-α)T内，信源可通过直达链路传输信息到选择的目的地Dk.此时，目的地Dk接收的信息yDk,2和对应的信噪比γDk,2分别为

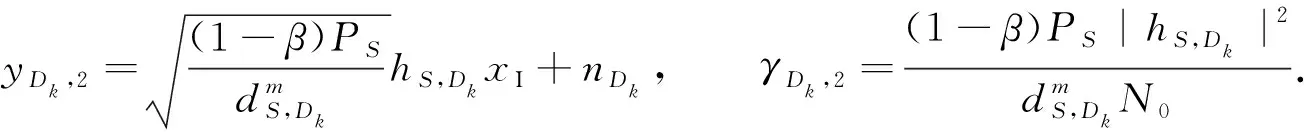
(16)

1.4 最大比合并传输

当源和目的地之间存在直达链路时，源既可以通过中继放大转发信息到目的地Dk，又可以通过直达链路传输信息到目的地Dk.目的地Dk采用最大比合并技术合并两路信息,故随机选择的目的地Dk接收的信噪比为

γDk=γDk,1+γDk,2.

(17)

2 延迟受限吞吐量分析

在延迟受限传输模式下，假定系统中断概率为pout，源节点信息传输速率为RS.由于无线信道是随机衰落的，系统传输可能会中断，故延迟受限吞吐量τDL可用中断概率进行表示，即

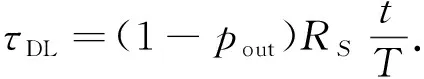
(18)

式(18)中：t为信息传输持续时间，t=(1-α)T.

由式(15),(17)可知，随机目的地选择策略下的系统中断概率可表示为

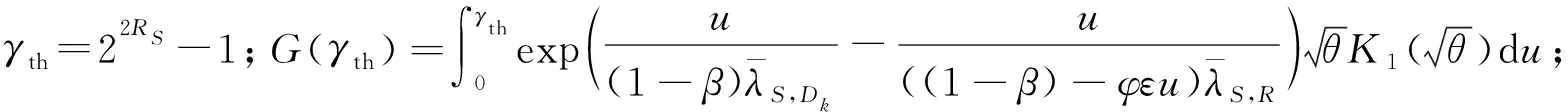
由于G(γth)在数学上难以处理，因此，利用高斯-切比雪夫积分[18]获得G(γth)的近似值，即

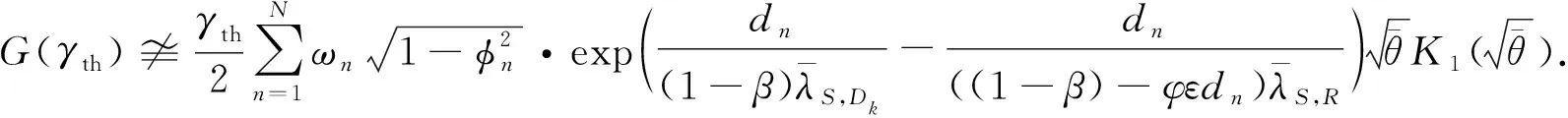
(20)

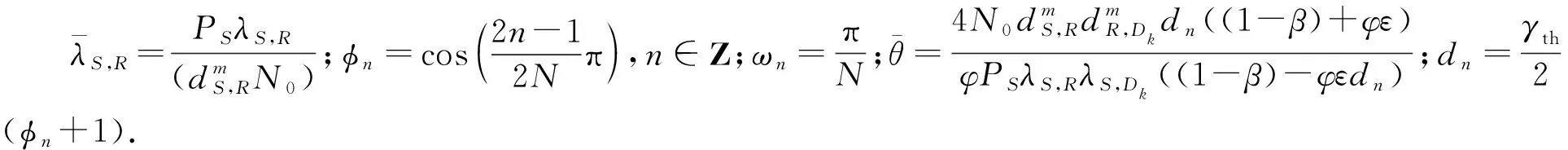
虽然式(20)中涉及N，但后面的仿真部分证实较小的N足以产生精确的G(γth)，故随机目的地选择策略下的中断概率pout和延迟受限吞吐量τDL可表示为

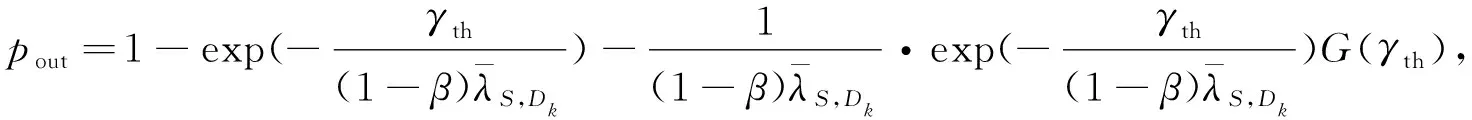
(21)

τDL=(1-α)(1-pout)RS.

(22)

最大化延迟受限吞吐量可通过解决以下问题获得，即

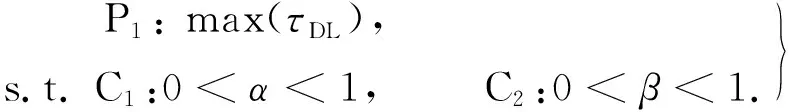
(23)

式(23)中：C1,C2是标准化约束.

由于式(23)涉及贝塞尔函数，α和β最佳值的闭合表达式难以获得,但可通过Matlab中的仿真进行数值评估得到最佳值.当0<α<1，0<β<1时，在β(或α)固定时，经求解可知，τDL对α(或β)的二阶偏导数都小于零，即τDL是α(或β)的凹函数.因此，优化问题(P1)相对于α(或β)是凸的，α和β的最佳值可通过一维穷举搜索获得.

3 目的节点选择策略

上文已对随机目的地选择策略下的延迟受限吞吐量进行研究，考虑系统存在多个目的用户节点，再提出3种目的节点选择策略(策略1～3)，并推导出3种策略下的系统中断概率和延迟受限吞吐量的近似闭合表达式.

3.1 策略1

通过直达链路，源节点S从K个目的节点中选择1个信道功率增益最大的，则选择的目的节点为

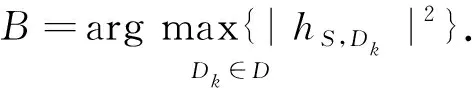
(24)

式(24)中：D={D1，…，DK}，表示K个目的节点的集合.

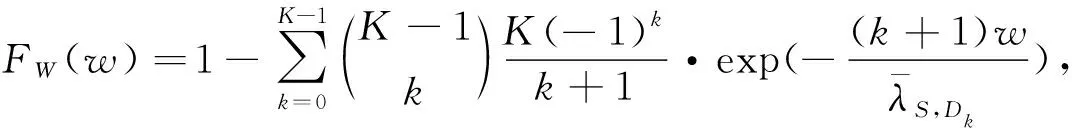
(25)

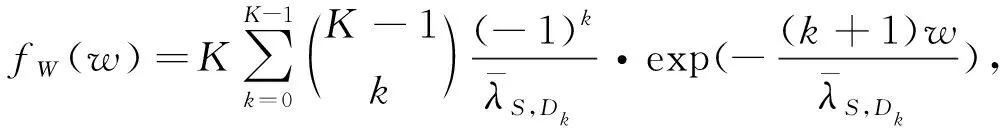
(26)

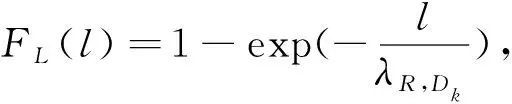
(27)

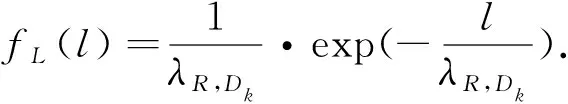
(28)

式(25)～(28)中：w,l为累积分布函数的自变量.

当源节点S通过中继链路传输信息到目的节点B时，节点B的接收信噪比γB，1为

仿照式(15)的求解过程，此时目的节点B的累计分布函数FγB，1(v)为

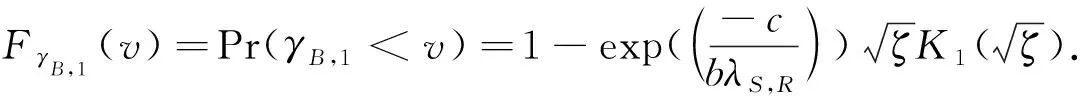
(30)

式(30)中：ζ=4a/(bλS，RλR,Dk).

当源节点S通过直达链路传输信息到目的节点B时，节点B的接收信噪比γB，2为

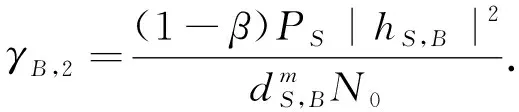
(31)

两路信息在目的节点B最大比合并后，系统的中断概率为

3.2 策略2

中继节点R从K个目的节点中选择1个信道功率增益最大的，则选择的目的节点B为

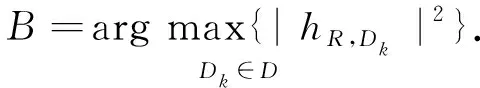
(33)

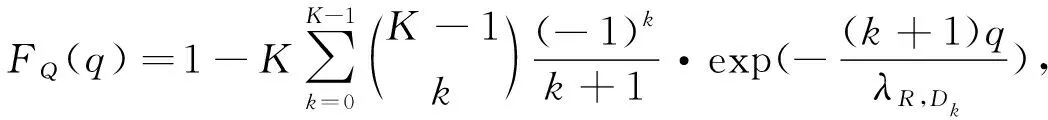
(34)

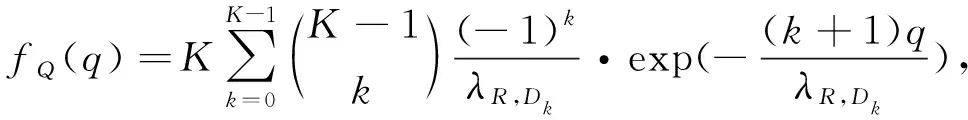
(35)

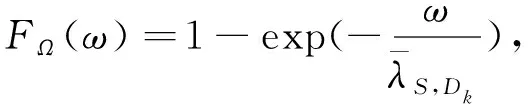
(36)

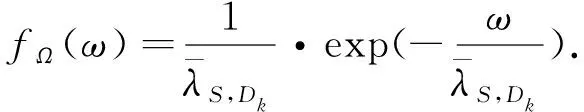
(37)

式(34)～(37)中：q，ω皆为累积分布函数的自变量.

同理，中继链路和直达链路在目的节点B处的接收信噪比γB，1，γB，2分别为

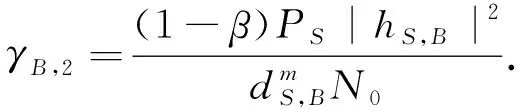
(39)

仿照式(15)的求解过程，通过中继链路传输时目的节点B处的累积分布函数FγB，1(v)为

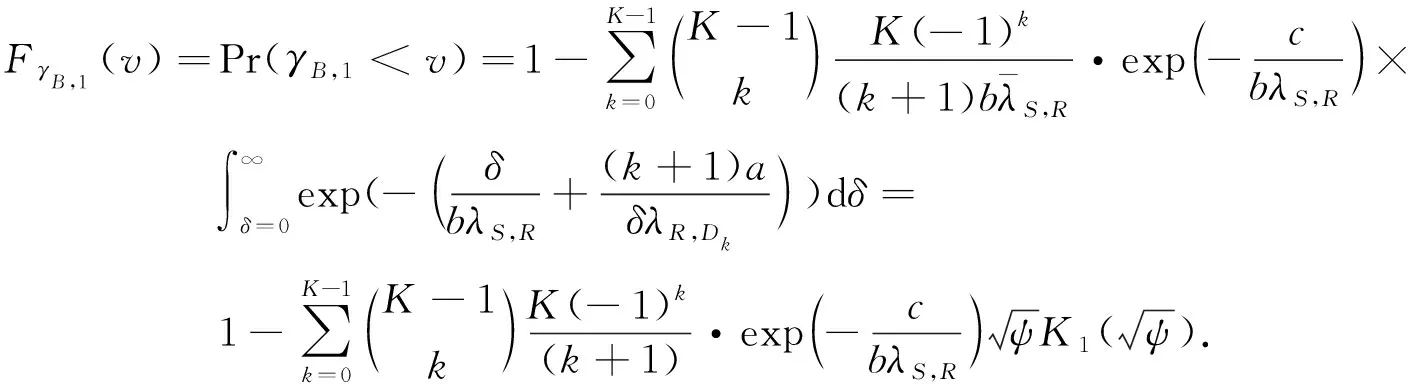
(40)

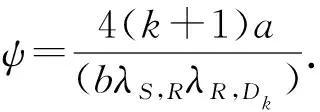
两路信息在目的节点B最大比合并后，系统的中断概率为

3.3 策略3

联合考虑来自于中继链路和直达链路的信噪比，选择能使总的接收信噪比最大的目的节点B为

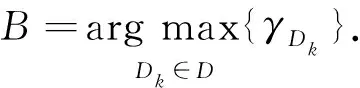
(42)

式(42)可以等价为选择能使中断概率pout最小的目的节点，称该选择策略为最佳目的地选择策略.因此，选择的目的节点B为

(43)

当系统存在K个目的节点时，由式(21)和次序量统计原理[19]可得系统的中断概率，即

pout,3=(pout)K.

(44)

3种策略的延迟受限吞吐量可表示为

τg=(1-α)(1-pout,g)RS.

(45)

式(45)中：τg∈{τ1，τ2，τ3}；pout,g∈{pout,1，pout,2，pout,3}.

4 数值分析与仿真

对延迟受限吞吐量进行数值分析和蒙特-卡洛(Monte-Carlo)仿真.为了使能量采集在短距离实用且有效，除另有说明外，系统参数的默认设置:源传输速率RS=2 bit·s-1，源发送功率PS=21 dB，能量采集效率η=1，路径损耗指数m=2.7.节点位置:源节点(0，0)，中继节点(0.25，0.25)，目的地(3，0).中继自干扰信道的平均信道增益为0.01，其他信道的平均信道增益均为1；各节点接收到的噪声方差N0=1 W；中继配备天线数NR=10；近似准确度参数N=20；目的地个数为1.为了确保数据的准确性与仿真的便利性，蒙特-卡洛仿真均执行105次循环.

延迟受限吞吐量τDL随时间切换比α和源功率分配比β的变化情况，分别如图3，4所示.由图3,4可知：数值分析结果与蒙特-卡洛仿真完全吻合，最佳吞吐量(即延迟受限吞吐量最大值)取决于所提协议的时间切换比α和源功率分配比β.

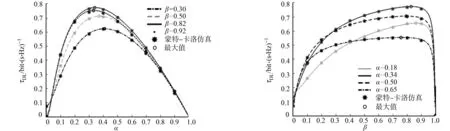
图3 延迟受限吞吐量随α的变化情况 图4 延迟受限吞吐量随β的变化情况Fig.3 Changes of delayed limited throughput with α Fig.4 Changes of delayed limited throughput with β

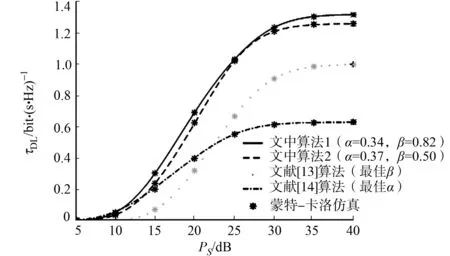
图5 延迟受限吞吐量随PS的变化情况Fig.5 Changes of delay limited throughput with PS

由图3可知：当α从0增至0.34左右时，最佳吞吐量从0增至0.78;当α从最佳时间切换值0.34(对应的β=0.82)增至1.00时，最佳吞吐量开始下降.由图4可知：当β为0.82时，可获得系统的最佳吞吐量.这是因为当时间切换比较小(α<0.34)时，采集能量较大，延迟受限吞吐量增加；反之，当能量收集时间较长，导致信息处理时间减少，延迟受限吞吐量性能降低.此外，当时间切换比α近似为0.34，且源功率分配比β为0.82时，可以获得系统的最佳吞吐量.因此，将α=0.34，β=0.82作为最佳吞吐量的近似优化值，并应用于以下仿真.

延迟受限吞吐量随PS的变化情况，如图5所示.由图5可知:当PS=40 dB时，文中算法1(α=0.34，β=0.82)的延迟受限吞吐量比文中算法2(α=0.37，β=0.50)、文献[13]算法(最佳β)和文献[14]算法(最佳α)多0.06,0.32，0.69 bit·(s·Hz)-1，故联合优化的最佳α(α=0.34)和最佳β(β=0.82)可以显著地提升延迟受限吞吐量.此外，文中算法2(α=0.37，β=0.50)的延迟受限吞吐量大约是文献[14]算法的两倍，体现出全双工技术的优越性.

在模拟环境下，策略1～3的延迟受限吞吐量随PS，K的变化情况，分别如图6,7所示.

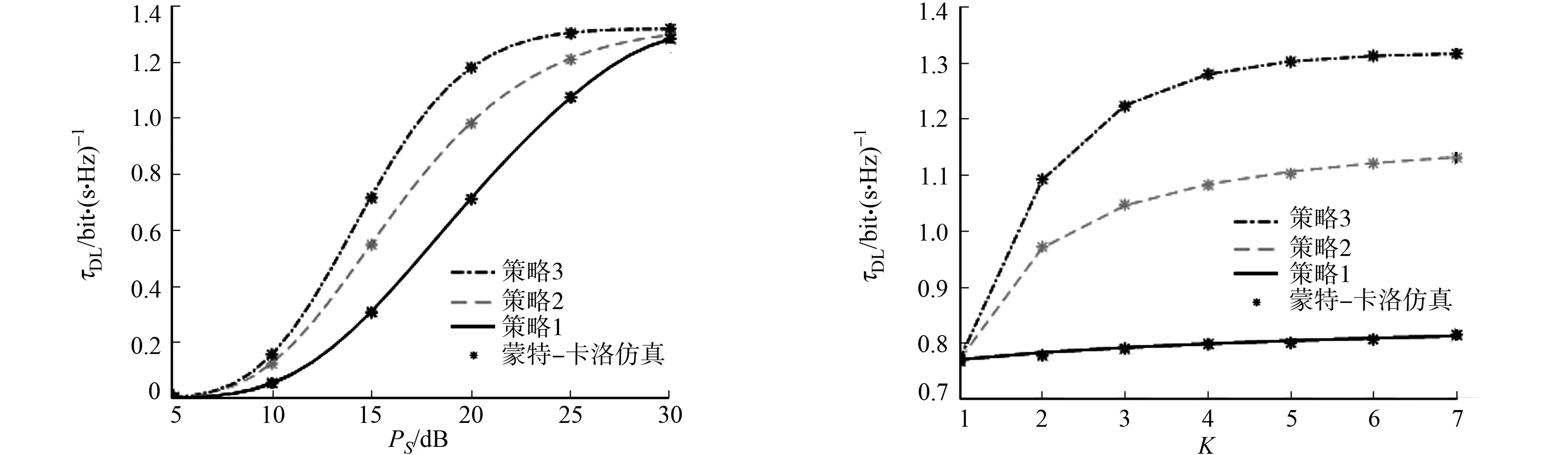
图6 不同策略下延迟受限吞吐量随PS的变化情况 图7 不同策略下延迟受限吞吐量随K的变化情况Fig.6 Changes in delay limited throughput Fig.7 Changes in delay limited throughput with PS under different strategies with K under different strategies

由图6可知：当K=3，PS=20 dB时，策略3比策略2的延迟受限吞吐量多0.20 bit·(s·Hz)-1，策略2比策略1的延迟受限吞吐量多0.26 bit·(s·Hz)-1，这体现出策略3的性能优势.

由图7可知：增加目的节点数量K可改善延迟受限吞吐量的性能，当其他参数固定时，随着K的增加，延迟受限吞吐量随之增加(式(32)，(41)，(44)，(45))；当K=4时，策略3比策略2的延迟受限吞吐量多0.20 bit·(s·Hz)-1，策略2比策略1的延迟受限吞吐量多0.28 bit·(s·Hz)-1，再次体现出策略3在提升延迟受限吞吐量性能方面的强大优势.

当源功率分配比β=0.82或时间切换比α=0.34时，随机目的地选择策略、策略1～3等4种策略下的延迟受限吞吐量随α，β的变化情况，分别如图8,9所示.

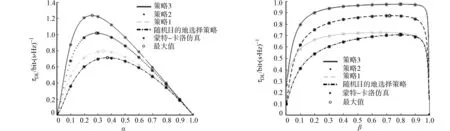
图8 不同策略下的延迟受限吞吐量随α的变化情况 图9 不同策略下的延迟受限吞吐量随β的变化情况 Fig.8 Changes of throughput limited throughput Fig.9 Changes of limited throughput throughput with α under different strategies with β under different strategies

由图8可知：当0<α<1时，随着α的增大，吞吐量先上升至最大值，再逐渐下降至0；当α=0.2时，与随机目的地选择策略相比，策略1～3的吞吐量分别提高0.12，0.37,0.61 bit·(s·Hz)-1.由数值分析结果可知：当β=0.82时，随着α的增大，能量采集阶段比信息传输阶段的时间逐渐增多，信息传输效率下降；当α超过最佳值时，吞吐量曲线从最大值开始呈下降趋势.

由图9可知：当0<β<1时，随着β的增大，吞吐量先上升至最大值，再逐渐下降至0；当β=0.2时，与随机目的地选择策略相比，策略1～3的吞吐量分别提高0.12，0.21，0.35 bit·(s·Hz)-1.由数值分析结果可知：当α=0.34时，随着β的增大，第二时隙内中继的发射功率随着第一时隙内中继采集能量的增加而增加，整个系统的吞吐量显著提高；当β超过最优值且越来越逼近1时，目的节点Dk的总接收信噪比γDk逐渐趋于0(式(17))；系统吞吐量随之逐渐趋于0(式(22)，(45)).

5 结论

基于时间切换能量采集协议，研究直达链路下的全双工放大转发协作中继方案.中继节点采用天线选择技术，目的节点处应用最大比合并技术；对于能量采集中继，在延迟受限传输模式中导出吞吐量的近似闭合表达式.数值分析和蒙特-卡洛仿真均表明，相较于文献[13]，[14]的算法而言，随机目的地选择策略在延迟受限吞吐量方面表现出更好的性能，且吞吐量的最大值取决于所提协议的时间切换比和源功率分配比.

此外，还对多目的地场景和最佳吞吐量进行研究，分析4种目的地选择策略，仿真并讨论不同策略下源发送功率PS、时间切换比α、源功率分配比β和目的地个数K对吞吐量的影响.分析表明，相较于随机目的地选择策略、策略1和策略2，策略3(最佳目的地选择策略)更适用于分布式多用户网络.