基于化学条件下静态释放模拟研究太行湖底泥TP分布特征

(山西省水文水资源勘测分局，山西 太原 030000)

底泥是湖库营养物质的重要蓄积库,污水的排入、地表径流汇集以及水生生物残骸,导致底泥中N、P元素逐步积累,易形成营养物质的内负荷。当外源排入湖库的N、P营养元素负荷量减少后,沉积物中的营养元素会逐步释放,成为湖泊富营养化的主导因子[1-2]。磷被认为是多数水体浮游藻类限制性营养元素，湖泊沉积物中磷的特征、水土界面间的行为以及沉积物释放规律研究，对探求湖泊富营养化防治意义深远[3]。

漳泽水库，又称太行湖(属于半封闭湖)，是人工湖泊，兴建于1959年，位于山西省东南部的长治市郊区，全湖区水面面积16.48km2(低水位时)，最深处位于库区泄水洞，约9m，库尾深1m，库中深4m，最高温度出现在8月，约29～32℃，结冰期为12月上旬至次年3月，低温为2～3℃，多年水体超过Ⅳ类水质，处于富营养化状态。2018年初次对湖区下游至湖尾均匀布设监测点1～16号(见图1)，监测底泥中总磷等污染物，并进行了室内静态化学条件下总磷等营养物质释放模拟试验，旨在湖区外源污染截断后，探究底泥对水体的二次污染情况。由于室外模拟的难度较大，所以采集底泥进行室内分析及静态模拟试验，通过近一年的底泥监测和室内静态模拟试验，基本掌握了湖区底泥总磷的分布情况及总磷释放初步特征，为解决水库的富营养化治理提供了参考。

图1 太行湖(漳泽水库)底泥总磷分布 (单位：mg/L)

1 湖区底泥中总磷(TP)分布特征

1.1 时间变化特征

全湖监测点总磷含量随时间变化特征见图2，最大值均出现在8月，其他月份变化不大，最小值均出现在10月，4月3～6号监测点出现最小值，与10月含量基本一致。总体变化规律为8月骤增，9月开始回落，到10月达到最低值，其后稍有回升。2号监测点9月回落缓慢，16号监测点10月回落值与7月起涨点达到水平。上述分布特征说明，污染物的主要来源是上游河流洪水期(8月)携带的大量泥沙及陆源污染物进入湖区，由于洪水期水动力条件强、水流快，造成整个湖区底泥TP含量增高，2号区域9月比其他区域高也说明大量泥沙等污染沉积后，一些细小的颗粒物继续向下游低凹区域运移沉积，16号监测点位于主河槽入湖口，9月后仍会有部分泥沙输入，但此时水动力条件减弱，大部分携带总磷的泥沙等停滞在此，造成TP比其他区域含量偏高。

图2 底泥中总磷(TP)随时间变化特征

1.2 空间变化特征

湖区总磷含量平均值为440mg/L,高值区位于坝址泄水洞区域和上游湖尾区，代表点为2号、14号、15号、16号，最大值为683mg/L,低值区在库中心偏向库区西侧区域，代表点为1号、4号、6号、7号、9号、11号。底泥总磷的空间分布不均衡(见图1)，湖区东侧总磷平均含量整体比湖区西侧高，有明显的东西带状分布特征，此种特征可能是太行湖近湖尾处绛河支流水质(Ⅱ类)好于南源(主源，劣Ⅴ类水质)水质所致。

2 总磷释放静态模拟试验

底泥中的磷释放与化学沉淀的形态有关，底泥中的磷主要以无机态的正磷酸盐为主，一旦出现有利于钙、铝、铁等不溶性磷酸盐沉淀物溶解的条件，磷的释放就可能发生[4]。

2.1 试验方法与试验计算公式

2.1.1 试验方法

将采集的湖区2号底泥原样带回实验室沥干重力水后放入试验容器底部(平铺5cm厚)，然后注入初始水样，浓度为C0(采集湖区2号底泥上覆水，由于浓度较高，所以将其释放至试验项目的Ⅲ类水质以下，称“稀释水”)，见表1。每隔12h取200mL水样检测，并添加同体积稀释水样于容器内，容器直径10cm，水柱高25cm，采样时于底部上方10cm处用虹吸管采取，以不扰动底泥，加稀释水时同样不能扰动底泥，如此反复，试验共进行5天(120h)停止。本次共设计25组试验，测试不同T、pH值、DO化学条件下试验释放水中的氨氮、总氮、总磷参数浓度变化，所有试验装置均置于室内自然光或日光灯照条件下。

表1 试验初始水样浓度 单位：mg/L

2.1.2 试验计算公式

模拟试验考虑影响底泥释磷主要因素：温度、溶解氧、pH值作用。营养盐释放试验不同文献的公式大体一致，但是诸多文献公式中各因素表述不一，下面列举一些文献中营养盐释放试验公式及其概念表述，并推导营养盐模拟释放试验公式。

2.1.3 文献计算公式及概念表述列举

a.计算沉积物的释放强度γ和γ′[3]：

(1)

γ′=r/A

(2)

式中：γ为每次采水样时的释放量，mg；γ′为释放强度，mg/m2；V为泥样上层水体积，L，取V=1L；Cn为第n次采样水中总磷浓度，mg/L；C0为泥样上层水起始总磷浓度，mg/L；Ca为添水后泥样上层水磷浓度，mg/L；n为采水样的次数；Vn为每次采水样体积，取Vn=35mL；A为与水接触底泥面积，m2，A=0.0133m2。

b.沉积物的释放强度[4-5]：

(3)

R=γ/(tA)

(4)

γ′=γ/A

(5)

式中:V为泥样上方水的体积,L,取V=1L;Cn为第n次采样时水中营养盐浓度,mg/L;C0为泥样上方水的起始营养盐浓度,mg/L;Ca为添加水后泥样上方营养盐浓度,mg/L;n为采水样的次数;Vn为每次采水样的体积，取Vn=100mL;γ为每次采水样时的释放量,mg;γ′为释放强度,mg/m2;R为释放速度,mg/(m2·d);t为释放时间,d;A为与水接触的底泥面积,m2,A=0.0133m2。每次采样后得出的R平均后即得到释放速度。

c.底泥中污染物释放率的计算公式[6-7]：

(6)

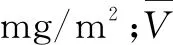
d.释放速率计算[8]：

(7)

e.底泥氮磷的释放通量采用下式计算[9]：

(8)

式中：Rn为到第n天为止底泥氮磷的释放量,mg；V为反应装置中剩余水样的体积,L；Ci为第i次采样时氮磷的质量浓度(i=1,2,…,n),mg/L；C0为初始氮磷的质量浓度,mg/L；Vi为第i次采取的水样体积,L。

f.柱状模拟释放营养物的释放速度按下式计算[10]：

(9)

2.1.4 营养物的释放量公式推导

设容器内柱状水体积为V(L)；各时刻释放浓度值为C0、C1、C2、C3、C4、C5、C6、C7、C8、C9、C10、…、Cn-1、Cn(mg/L)(见表2)；每隔t时段取样检测，取样体积Vi，同时补充同体积水样至原刻度线，保证容器内水柱体积V不变。因为取某一浓度水样后，再将另一浓度(设为Cai，i=1,2,3，…，n)的水样(应满足低于取样时的浓度)回加进去，这时容器内的浓度会发生变化，成为下一时段营养盐释放的起始浓度。用后一时刻容器中某物质的量(mg)减去前一时刻起始量(见表3)，即为某时段某营养盐的释放量，将各时段的释放量累加，即为试验期(nd)某营养物质释放通量R(mg)，如果是氨氮可考虑容器的内上层空间聚集的收集量。如果收集不到，计算通量可能会偏小。

表2 释放试验期各时间点营养物质浓度

表3 某时刻取出再回填同体积(Vi)水样后容器内某物质量

各时段释放量计算如下：

0d释放量：

0

0～1d释放量：

VC1-VC0

1～2d释放量：

VC2-[VC1-Vi(C1-Ca1)]

2～3d释放量：

VC3-[VC2-Vi(C2-Ca2)]

3～4d释放量：

VC4-[VC3-Vi(C3-Ca3)]

4～5d释放量：

VC5-[VC4-Vi(C4-Ca4)]

……

(n-2)～(n-1)d释放量：

VCn-1-[VCn-2-Vi(Cn-2-Can-2)]

(n-1)～nd释放量：

VCn-[VCn-1-Vi(Cn-1-Can-1)]

将上述各时段释放量相加得

R=VCn-[VC0+Vi(C1-Ca1)]+Vi(C2-Ca2)+Vi(C3-Ca3)+…+Vi(Cn-2-Can-2)+Vi(Cn-1-Can-1)

即：

i=1,2,3,…,n

(10)

上述公式即为底泥某营养盐释放通量公式。则底泥释放强度公式为

γ′=R/A

(11)

释放速率公式为

γ=R/(tA)

(12)

式中：R为底泥某营养盐试验期的释放通量，mg;V为泥样上方水的体积，L;Cn为第n次(试验终止时)采样时容器内水中营养盐浓度，mg/L;C0为泥样上覆水初始某营养盐浓度，mg/L;Vi为每次采水样体积，L;Ci-1为第i-1次采样时容器内上覆水中某营养盐浓度，mg/L;Cai-1为第i-1次所添加的水体中某营养物质浓度，mg/L;γ′为释放强度，mg/m2;γ为释放速率，mg/(m2·d)；t为释放时间，d;A为与水接触的沉积物表面积，m2。

经过上面推导明确了各符号代表的含义，验证了底泥营养盐释放量的经典计算公式。

2.2 试验结果分析

2.2.1 温度(T)对底泥总磷(TP)释放影响试验

设计pH=7，DO=8.0mg/L，试验温度15℃、20℃、25℃、30℃对底泥总磷(TP)释放的影响。

根据上述推导的释放计算公式计算出pH值和DO一定时不同温度下总磷(TP)的释放强度和释放速率，见图3、图4。总磷释放强度在不同温度下均为上升趋势，25℃、30℃释放强度比15℃、20℃上升快，30℃时释放强度上升最快，TP释放速率初始下降非常快，48h后下降减缓，随时间增加释放速率趋于稳定，不再下降，30℃时释放速率最大。从图3、图4可以看出，温度升高有利于总磷的释放，并且温度升高，微生物的活性增强，促进生物扰动、矿化作用和厌氧转化，导致间隙水耗氧增加，使环境向还原态转化，利于Fe3+向Fe2+转化，促使底泥中磷释放。此外，微生物的活动还可使底泥中的有机态磷转化成无机态的磷酸盐而得以释放。太行湖的最高温出现在8月(30℃左右)，因此，底泥中总磷含量此月也最高，总磷释放均高于其他月份。

图3 不同温度下总磷(TP)释放强度(γ′)曲线

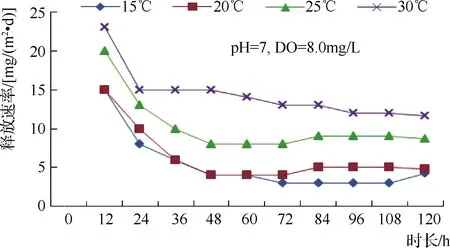
图4 不同温度下总磷(TP)速率(γ)曲线

2.2.2 pH值对底泥总磷(TP)释放影响试验

设计温度20℃，DO=8.0mg/L，试验不同pH值(5、7、9)时对底泥总磷(TP)的释放影响(通过多年DO检测，2号区DO较高，在5～13mg/L之间，DO随温度升高而降低，随湖区水深而降低，通过现场监测，检测结果见表1)，通过太行湖区BOD5检测，DO=8.0mg/L时，20℃条件下BOD5=0.5左右，DO降低可以接受。7月湖区2号位置DO检测结果见表4。

表4 7月湖区2号位置DO检测结果

据上述释放计算式得20℃，DO=8.0mg/L时不同pH值条件下总磷的释放强度和释放速率(见图5、图6)。总磷释放强度(γ′)在不同pH值条件下均呈上升趋势；pH=10时平均释放强度最大，明显偏高于其他组，初始下降速度也最快，其次为pH=9时释放速率较大,pH=7、pH=5平均释放速率最小，趋势基本一致。60h后释放速率趋于稳定。

图5 不同pH值条件总磷(TP)释放强度曲线

图6 不同pH值条件总磷(TP)释放速率曲线

2.2.3 溶解氧(DO)对底泥总磷(TP)释放影响试验

设计温度20℃，pH=7，试验不同DO条件下(DO指试验初始值，且常年DO监测值较高，底泥耗氧试验，基本是15h后略有下降，文中不再列举)对底泥总磷(TP)的释放影响。由图7、图8可知，总磷释放强度在不同DO条件下均呈上升趋势，但处于低氧(DO=2.0mg/L)时释放强度和释放速率最大。好氧(DO=8.0mg/L)时释放速率最小，60h后释放速率均趋于稳定。

图7 不同DO条件下总磷释放强度曲线

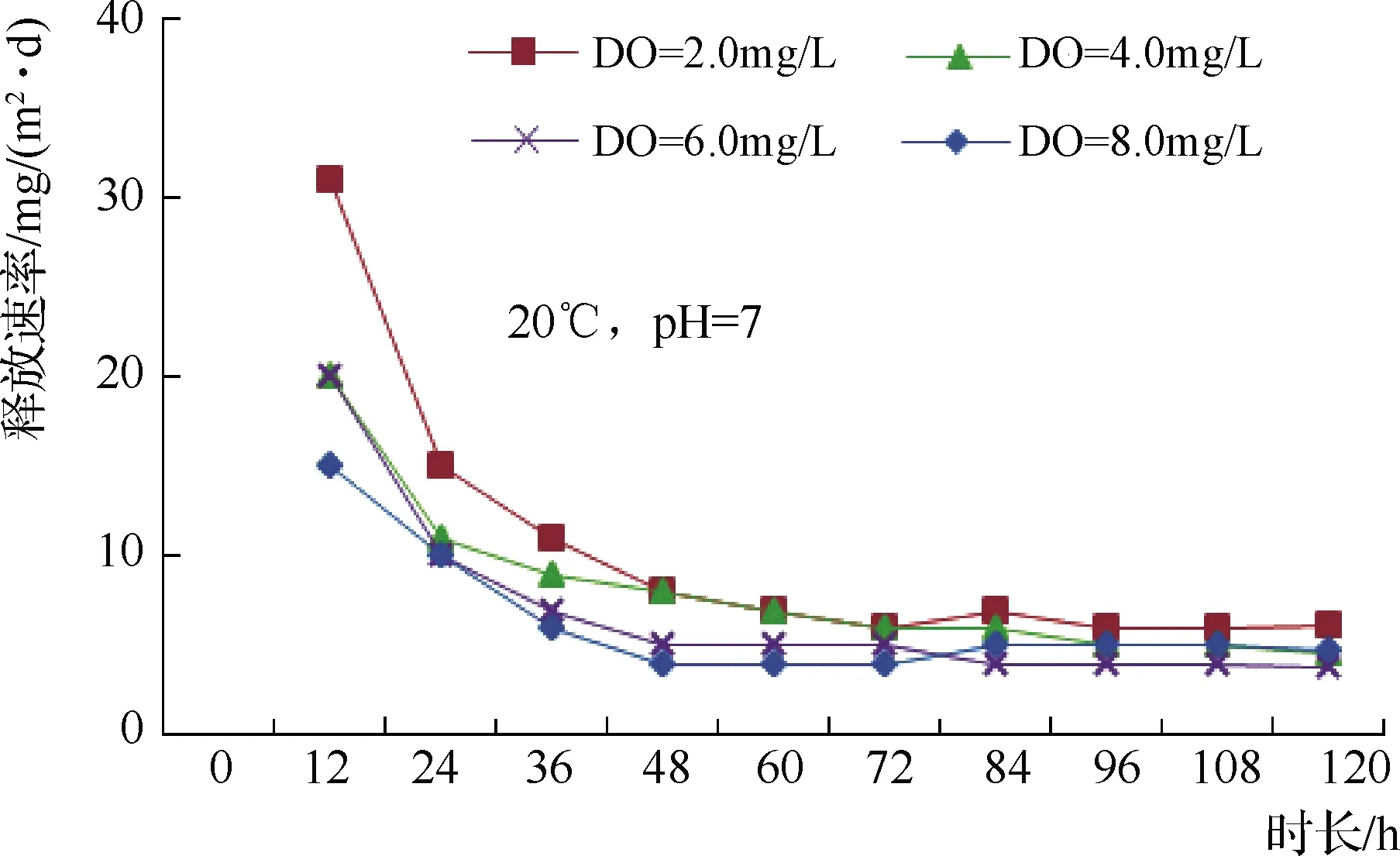
图8 不同DO条件下总磷释放速率曲线

但在好氧状态下，不是所有形态的磷都不会释放，底泥中的有机质就会受到微生物的好氧分解，使不溶性的有机磷变成无机磷，易于释放。只是由于底泥中的有机磷含量一般较低，或是产生的腐殖质的吸附性释放量不大，所以，总的影响结果是在好氧状态下，底泥中磷的释放量会降低。

2.3 总磷释放强度数学模型推求

2.3.1 数学模型一

自变量为温度(T)、pH值、溶解氧(DO)，因变量为总磷(TP)平均释放速率(γ)，建立多元线性回归模型，借助SPSS软件实现，则数学模型如下：

γTP=-45.429+0.953(T)+4.2(pH)+1.295(DO)

(13)

模型复相关系数：

R=0.754a

式中：γTP为总磷(TP)的平均释放速率，mg/(m2·d)。

方差检验：假设显著性水平a=0.05时(即1-a=95%)，自变量m=3，样本n=25，则自由度(df)为(m,n-m-1)=(3，21)，由F检验临界值表(α=0.05(a))查得F0.05(3，21)=3.073，由表5得知方差检验F=9.249>3.073，概率P(sig)=0.000a<0.05，说明方程回归显著。

2.3.2 数学模型二

将释放试验的初始浓度值(C0)引入模型，自变量为C0、温度(T)、pH值、溶解氧(DO)，因变量为总磷(TP)的平均释放速率(γ)，则多因子线性回归数学模型见式(5)，借助软件spss实现，其数学模型如下：

γTP=8.897+0.43(T)+2.087(pH)+0.064(DO)-1136.97(C0)

(14)

模型复相关系数：

R=0.844a

式中:γTP为总磷(TP)的平均释放速率，mg/(m2·d)。

总磷(TP)多元线性回归模型方差检验：假设显著性水平a=0.05时(即1-a=95%)，自变量m=4，样本n=25，则自由度(df)为(m,n-m-1)=(4，20),由F检验临界值表,α=0.05(a),查得F0.05(4，20)=2.866，由表4得知方差检验F=12.364>2.866，概率P(sig)=0.000a<0.05，说明回归方程显著。数学模型一、模型二拟合结果见图9、图10。

图9 模型一总磷(TP)释放速率拟合曲线

2.4 模型外推预测

模型检验合格后可用于外推预测。分别用模型一和模型二进行外推预测，漳泽水库底泥总磷(TP)年释放量按下式计算：

图10 模型二总磷(TP)释放速率拟合曲线

(15)

式中：W为湖库磷释放量，t；γi为第i种条件下氮释放速率，mg/(m2·d)；ΔTi为第i种条件所代表的时间段，d；A为湖库水面面积，m2。

以2018年实测数据为基础，预测2018年漳泽水库沉积物中总磷的月平均释放速率γTN和释放量W，见表5。

表5 2018年沉积物中TP释放量预测

从表5可以看出，如采用模型一，漳泽水库沉积物中总磷表现为全年释放反应，合计释放量57.40t；如采用模型二，5月和8月沉积物中总磷表现为释放反应，合计释放量5.20t，其余月份表现为负释放，沉积量为182.00t，全年合计沉积量177.00t。

2.5 合理性验证

调查显示，漳泽水库2018年渗漏量和下泄流量总计1.25亿m3，2018年底蓄水量为8487万m3，较2017年底减少3677万m3。库区代表断面总磷平均浓度由2017年的0.061mg/L降至2018年的0.054mg/L。外部点源污染物总磷为22.60t/a，面源污染物总磷为840.00t/a。

考虑到面源污染中氨氮以颗粒物携带为主，多在进入水库后先行沉淀，而释放试验释放速率则以监测上覆水中TP浓度得出，为更为准确地验证内源释放量，调查了入库站点的污染量，其中浊漳河南源、绛河以及碧头河2018年TP入库量合计79.50t。通过质量守恒验证，2018年漳泽水库的外源总磷污染量为107.00t/a，通过下泄和渗漏仅排出TP污染物6.75t/a，由于水体总磷浓度和蓄水量减少，水体中溶解态TP量也较上年减少2.72t/a，其内源释放量约为-103.00t/a，即水体中TP向沉积物中沉淀103.00t/a，与模型二结论基本一致。因此采用模型二外推结论，即2018年漳泽水库沉积物总磷释放量小于沉积量，表现为水体中溶解态总磷向沉积物中的沉积吸附反应，全年沉积总磷103.00t。

3 结 论

通过分析太行湖底泥中总磷含量的时空分布特征及在静态试验条件下改变环境因子模拟太行湖底泥总磷(TP)释放，得出如下结论：

a.太行湖底泥受洪水影响8月总磷含量最高，10月含量最低，库区西侧近绛河支流区域4月TP含量较低，比10月略低。空间分布为上游入湖口与下游坝址东侧泄水洞区域TP含量为高值区，湖区TP含量存在明显带状分布，总体为湖区东侧高于西侧区。

b.底泥释放TP强度随温度升高而增加；随pH值增加释放强度增加；随DO减小释放强度增加。

c.太行湖底泥总磷(TP)平均释放强度模型，试验25组样本建模为γTP=-45.429+0.953(T)+4.2(pH值)+1.295(DO)，R=0.754a，试验组14组样本建模为γTP=8.897+0.43(T)+2.087(pH值)+0.064(DO)-1136.97(CO)(DO)，R=0.844a。

d.经模型二预测2018年底泥释放磷量为5.20t,总体沉积177.00t，占外源TP输入量的4.8%。

通过对湖区底泥总磷含量分析和基于化学条件下总磷静态释放模拟，外源(面源为主)仍是太行湖库主要污染源，在外源磷输入截断后，内源底泥释磷将成为其水体富磷主要因素，会引发二次水体磷污染，再度造成水体富营养化。本次监测湖区底泥总磷分布特征及释磷模拟试验，为湖区污染治理及生态修复提供了技术参考。限于各方面条件，没能进行室外现场模拟，本次室内试验只进行了化学条件下静态释放模拟研究，是本文的缺陷所在，以后将进一步对太行湖区底泥展开动态条件和微生物影响条件下的磷释放进行研究。