BDS/GPS组合导航定位研究

陈 亮，李 超，师鹏宇，展 昕

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081；2.北京卫星导航中心，北京 100094；3.中国人民解放军92493部队，辽宁 葫芦岛 125000；4.中国船舶重工集团公司第七二二研究所，湖北 武汉 430205)

0 引言

BDS/GPS组合导航定位通过不同系统观测数据的分列误差方程来实现联合求解未知参数。这种在原始数据层面的组合解算方法可以最大限度地发挥多系统组合的优势。这种定位处理模式需要观测卫星5颗或以上GPS/BDS卫星，未知参数包括三维位置、接收机钟差和系统时差[1]。这种模式每个历元都将系统时差作为新的未知量进行解算，计算思路简单。如果能获取比较稳定的系统时差，将系统时差作为常数进行定位解算，并将系统时差信息进行累积平滑处理。观测时间越长，所得到的系统时差精度就越高，在后续的导航定位解算中，对位置计算精度贡献越大[2-4]。大多数已有文献都是针对事后多系统或加入其他外部观测量进行处理，本文研究重点为如何获取高精度的系统时差，提出一种改进的组合定位方法，采用二阶高斯马可夫过程模型建模系统时差。将获取的时差再进行组合定位处理，试验结果表明该方法可以有效提高组合导航定位精度。

1 普通组合定位算法

在应用BDS/GPS组合定位前，首先要对BDS/GPS导航系统进行时间系统与坐标系统的统一[5]。BDS参考框架为CGS2000和GPS参考框架为WGS84，这2种坐标系实际上都是国际地球参考框架(ITRF)的一种实现[6]，这2个框架之间的差值应该在cm量级，对于大多数用户来说，这样的差异可以忽略不计[7-8]。BDS时间系统为BDT，GPS时间系统为GPST，其偏差可通过2种方式求得：一种是广播星历获取；另一种是通过组合定位解算获取。

1.1 广播星历获取法

通过BDS播发的广播星历参数可求得BDT与GPST的时差。通过BDS广播星历计算：

ΔtSystems=tBD-tGPS=

A0G+A1G[TOW-t0G+604 800((WN-WN0G)mod64)]，

(1)

式中，A0G为GPS和BDT时间差的常数偏移量；A1G为GPS和BDT时间差的偏移变化率；t0G为GPS和BDT时间差的偏移数据的参考时间；WN0G为GPS和BDT时间差的偏移参考周计数[9]。

1.2 组合定位算法

当观测卫星数量大于等于5颗时，采用最小二乘原理进行数据处理。假设观测了n颗GPS卫星和m颗BDS卫星。δtGPS为接收机与GPS系统时差，δtBD为接收机与BDS系统时差[10]。误差方程为：

vi=Aixi+Li。

(2)

x是未知参数向量：

x=[δXδYδZδtGPSδtBDS]T。

(3)

v是残差向量：

v=[v1v2...vn+m]T。

(4)

A是设计矩阵：

(5)

L是观测伪距残差：

L=[(ρ0-ρi) (ρ0-ρ2)...(ρ0-ρn+m)]T，

(6)

式中，ρ0为卫星至接收机的距离；ρi为观测伪距。最小二乘解为：

(7)

在使用BDS/GPS普通组合定位时，每个历元都将系统时差作为新的未知量进行解算。该模式计算方式简单，普遍应用于组合定位处理。

2 改进组合定位算法

目前全球卫星导航系统中，各个卫星导航系统都维持着自己的系统时间，在导航地面站钟组的统一控制下，不同导航系统的卫星对应调整自己的星载原子钟时间，将卫星的系统时间与地面钟组所产生与保持的系统时间保持一致[11-12]。根据已公布的信息，GPS系统时间标准维持精度小于10 ns[13]，BDS系统时间标准维持精度小于50 ns[14]。

系统时差数值在一段时间范围内波动不是很大，比较稳定，因此可以利用系统时差值辅助组合定位[15]。此时需要解算的未知数个数有所减少，几何精度因子得到优化。并且在各种恶劣条件下，如卫星接收数减少情况下继续提供定位服务，提高了导航系统的可用性[16-18]。

设δtSYS为系统时差：

δtSYS=δtGPS-δtBDS。

(8)

x是未知参数向量：

x=[δXδYδZδtSYS]T。

(9)

A是设计矩阵：

(10)

L是观测伪距残差：

L=[(ρ0-ρ1) (ρ0-ρ2) ... (ρ0-ρn)·

(ρ0-ρn+1-δtSYS)...(ρ0-ρn+m-δtSYS)]T。

(11)

最小二乘解为：

(12)

改进的组合导航定位流程图如图1所示。系统时差的精度是改进组合导航定位实现的关键。

图1 改进的组合导航定位流程Fig.1 Improved integrated navigation and positioning flow chart

3 系统时差滤波算法

采用二阶高斯马可夫过程模型来模拟系统时差特性用微分方程表示如下：

(13)

式中，ω0为自然频率；β为小于1阻尼比；ω是具有单位谱密度的高斯白噪声。

构建卡尔曼滤波方程，将式(13)转化成一个线性、离散的时间系统。

状态方程为：

Xk+1=Φk，kXk+Γkwk。

(14)

观测方程为：

Zk=HkXk+vk，

(15)

(16)

过程噪声方差矩阵为：

(17)

式中，q1为钟差白噪声的频谱幅度，q1=2γ；γ根据不同的时钟类型取不同的值，本文中取值为2×10-20；q2为频差白噪声的频谱幅度，q2=8π2α；α也根据不同的时钟类型取不同的值，本文中取值为4×10-29；Δt为采样时间间隔，取值1 s。

其滤波增益阵为：

K(k)=P(k-1/k-1)HT(k)

[H(k)P(k/k-1)HT(k)+R(k)]-1。

(18)

根据新的观测值z(k)得到：

(19)

计算滤波估计方程：

(20)

将滤波估计进行保存，等待下一时刻得到新的观测值，重复上述计算过程。

4 验证分析

数据采集设备如图2所示，接收机采用卫星导航双系统接收机，可实现对BDS系统和GPS系统卫星跟踪捕获。天线采用宽频段抗多径天线，实现GPS、BDS导航系统导航信号接收与放大。

测试时间为2019年6月2日17：40：35，接收机天线位置纬度38.115 45°，经度114.325 68°，高度为75.35 m。大地直角坐标X轴-2 069 742.787 90 m，Y轴4 578 499.621 77 m，Z轴3 915 580.619 77 m。采样周期为1 Hz，采集16个小时的观测数据，卫星仰角设置为10°并忽略多路径影响。然后对B1I/L1CA伪距观测值分别使用不同组合方式进行定位解算。

图2 数据采集设备Tab.2 Data acquisition equipment

为了分析不同组合方式对定位精度的影响。分别应用普通组合模式和改进后组合模式进行定位解算，并将结果与已知精确坐标进行比较。统计其(X/Y/Z)分量的差异，如表1所示。同时给出了普通组合模式和改进后组合模式的定位结果时间序列图，如图3和图4所示。图5和图6分别给出了组合定位观测时段中观测卫星数目和GDOP值。

表1 定位误差分析 m

表1可以得到采用了不同的处理策略，定位结果却存在差异，普通组合模式经过统计分析三维定位精度分别为12.14，7.97，6.05 m。改进后组合模式经过统计分析三维定位精度分别为8.64，6.42，5.12 m。改进后组合模式定位精度较普通组合模式有所提高。

由图3和图4分析可得普通组合模式定位存在很多跳跃点。由图5和图6分析可得在跳跃点处存在卫星升起和卫星下降的卫星切换过程。在改进组合定位模式中由于对时差进行滤波处理后，减少了噪声影响，解算时差精度长期稳定。在卫星上升和下降过程中都能提供相当好的估计值，在观测条件变化的情况下也能够获得较高定位精度。所以改进组合定位算法对卫星星座的几何分布敏感性低。适用于各种条件下的组合定位。

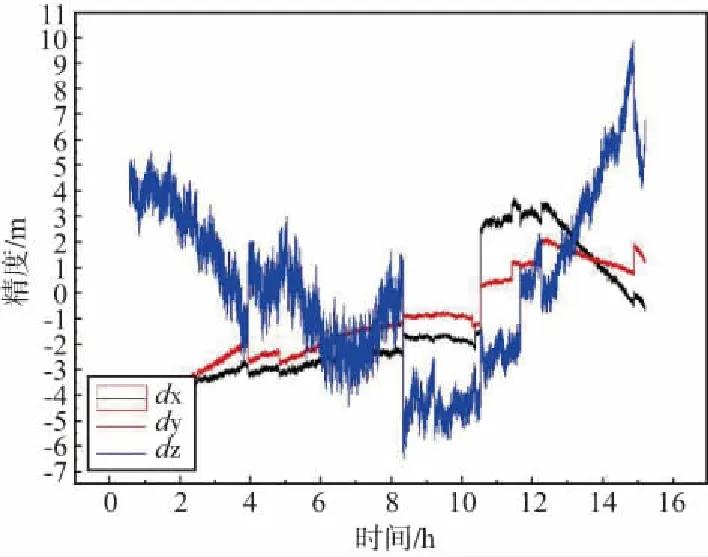
图3 普通组合定位精度Fig.3 General combined positioning accuracy

图4 改进组合定位精度Fig.4 Improved integrated positioning accuracy

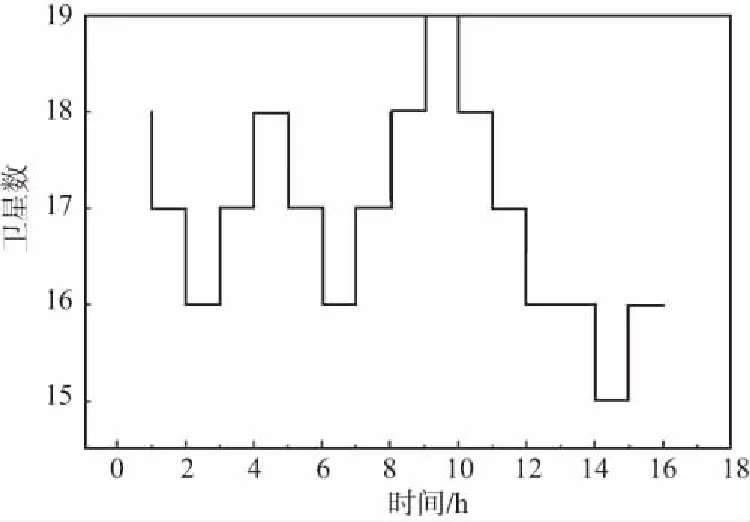
图5 观测卫星数目Fig.5 Number of observation satellites

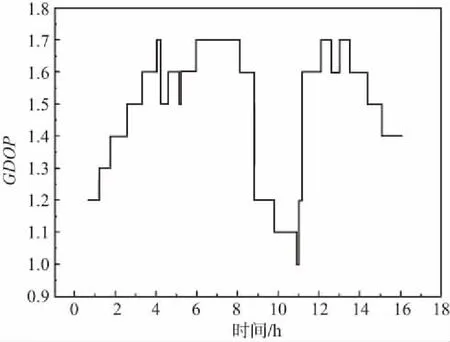
图6 GDOP值Fig.6 Value of GDOP

5 结束语

针对BDS/GPS组合导航定位进行了深入研究，提出一种改进的组合定位方法。通过采用二阶高斯马可夫过程模型对系统时差进行建模，获取的高精度系统时差再进行组合定位处理。试验结果表明，在由于卫星数量变化而引起的星座结构变化时引起的定位跳跃在经过时差建模再处理后可有效地进行改善。对于卫星星座结构较差的观测环境，由于卫星少于5颗无法实现组合定位，但是估计出系统时差的基础上进行组合定位可极大地提高组合导航定位的应用，并且对定位精度也有较大的改善，本文的结论可为各种组合导航定位应用提供良好的理论支撑。