一种基于失效概率相对误差估计的可靠性分析方法

张毅博， 孙志礼， 闫玉涛， 王 健

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

随着机械结构的日趋复杂，基于代理模型(如响应面RSM[1]、神经网络NNs[2]、支持向量机SVM[3]、Kriging[4-7]等)的可靠性分析方法由于其高效性和准确性而越来越受到重视.Kriging模型作为一种精确的内插方法，在提供预测响应的同时还给出了预测响应的方差，这使得Kriging模型在可靠性分析中得到了广泛应用并逐渐成为研究热点.

近年来，为改善Kriging模型的精度和可靠性分析效率，众多学者提出了各种自适应试验设计策略和可靠性分析方法，其中，基于学习函数的选点策略是研究最广泛的.例如，Bichon等[8]提出了学习函数EFF，用以测量样本接近极限状态的程度；Echard等[9]定义了学习函数U，用以选择最容易错分类的样本；Sun等[4]通过提出的学习函数LIF来选择对失效概率预测精度改善最大的样本.此外，学者们还从采样区域[10]及交叉验证[11]等方面发展了各种选点策略.然而，现有自适应试验设计的停止准则主要聚焦于单个样本满足学习函数的要求，而不是从预测的失效概率满足可靠性分析精度需求的角度出发，这往往会增加不必要的功能函数调用次数，降低可靠性分析效率.为此，Hu等[12]和Wang等[13]基于失效概率的相对误差估计提出了两种新的停止准则；然而，由于保守或错误地估计真实失效样本数的取值范围，新的停止准则仍难以应用到工程实际中.

针对上述存在的问题，本文基于失效概率的相对误差估计提出了一种更精确的真实失效样本数的区间估计方法，从而有效地避免了不必要的功能函数调用和错误的失效概率评估结果，并采用两个实例来说明所提方法的通用性、准确性及高效性.

1 可靠性分析基本理论

在可靠性领域中，失效概率被定义为

(1)

式中：x为N维随机向量(即N个影响结构输出的随机输入因素)；f(x)为x的联合概率密度函数；G(x)为结构的功能函数且G(x)将x的空间分为两部分，即失效域{x|G(x)≤0}和安全域{x|G(x)>0}.

在Kriging模型中，G(x)被表示为

G(x)=g(x)Tβ+z(x) .

(2)

式中：g(x)为多项式回归基函数；β为相应的回归系数，本文令g(x)的阶次为0；z(x)为高斯过程.z(x)具有如下特征：

E[z(x)]=0，Cov[z(x),z(w)]=σ2R(x,w;θ).

式中：σ是高斯过程z(x)的标准差；R(x,w;θ)表示z(x)和z(w)间含未知参数θ的相关系数.本文采用应用最广泛的高斯相关函数：

(3)

式中：xk，wk，θk分别表示x，w和θ的第k个元素.

在给定含M个训练样本的初始DoE(design of experiments)下，β和σ的估计分别为

(4)

(5)

式中：g=[g(x1),g(x2),…,g(xM)]T,R=[R(x,w;θ)]N×N.

参数θ由极大似然估计得到：

(6)

为确保预测响应最小方差无偏性，样本x处的Kriging预测响应及其方差分别为

(7)

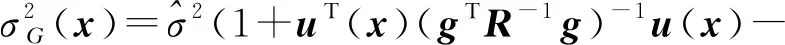
(8)

式中：

r(x)=[R(x1,x;θ),R(x2,x;θ),…,R(xM,x;θ)],

u(x)=gTR-1r(x)-1.

因此，结构失效概率的估计值为

(9)

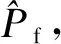
(10)

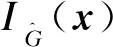
(11)

(12)

2 失效概率的相对误差估计

2.1 学习函数U

Echard等[9]从样本符号预测精度的角度出发定义了一个学习函数U来量化符号预测的不确定性，其表达式为

(13)

则该样本x处符号预测错误的概率为

Perror(x)=Φ(-U(x)).

(14)

式中,Φ(·)为标准正态分布的累积分布函数.

显然，μG(x)越小(样本x越接近极限状态G(x)=0)或σG(x)越大(样本x的不确定性越高)或两者兼之，则U(x)值越小，样本x处符号越容易预测错误.因此，定义U(x)最小的点为新训练样本，即

(15)

基于函数U的自适应可靠性分析流程如下：

① 在[-5, 5]N空间内采用拉丁超立方抽样(LHS)定义初始训练样本集Ω，并应用MC法产生候补样本集ΩCS；

② 基于样本集Ω，构建Kriging代理模型，并根据式(7)、式(8)和式(13)找到样本集ΩCS中对应的最小U值min(U(x))，如果min(U(x))>2，停止迭代，由式(10)～式(12)计算可靠性结果，否则继续步骤③；

③ 计算新训练样本x*处的功能函数值G*，将其加入到初始训练样本集Ω中，并返回步骤②.

2.2 相对误差估计方法

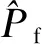
(16)

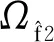
(17)

忽略Kriging预测之间的相关性，则Ssw和Sfc均服从泊松二项分布，其分布参数为

(18)

(19)

式中：Ui=U(xi);Uj=U(xj).

随着Kriging模型精度的逐渐改善，U(x)≤2的样本数逐渐减少，文献[13]采用的林德伯格-费勒中心极限定理不再适用.此外，根据Le cam定理定义的误差界限可知，只有在样本符号预测正确或错误的概率较小时，泊松分布才能较好地近似泊松二项分布.因此，本文采用适用性更广泛且近似效果优于泊松分布的正态分布来模拟Ssw和Sfc的分布，即

(20)

因此，Nf2的分布为

(21)

在置信水平为0.95时，Nf2的置信区间为

[μNf2-1.96σNf2,μNf2+1.96σNf2].

(22)

文献[12]将Nf2的取值区间定义为

(23)

文献[13]将Nf2的取值区间定义为

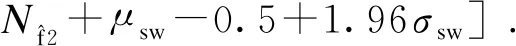
(24)

(25)

本文令α=0.1，则失效概率估计值的相对误差为

(26)

因此，只要式(26)中失效概率的最大相对误差εmax满足式(27)中的条件，就说明满足可靠性分析的精度要求.

εmax≤εthr.

(27)

式中,εthr为最大相对误差的阈值，工程实际中εthr一般为0.01～0.05[12-13]，本文取εthr=0.03.

2.3 基于相对误差估计的可靠性分析

基于相对误差估计的自适应可靠性分析方法的基本步骤如下：

步骤1 采用LHS法产生初始训练样本集SDoE，并计算相应的真实功能函数值GDoE.初始训练集SDoE一般只需少量的样本，在后续迭代选点过程中不断更新训练集.

步骤2 基于现有DoE和MATLAB中的DACE工具箱构建Kriging模型，并应用MC法产生候补样本集ΩCS.

步骤3 计算候补样本集ΩCS相应的μG(x)，σG(x)和U(x)；根据式(26)获取失效概率估计值的最大相对误差εmax，如果不满足式(27)，将样本集ΩCS中最小U值min(U(x))对应的样本作为新训练样本加入到DoE中并返回步骤2；否则，继续下一步.

步骤4 应用MC法估计失效概率及其变异系数，如果变异系数满足式(28)，则停止迭代并输出可靠性分析结果；否则，扩大MC样本数并重复步骤2～4，直至满足式(28).

(28)

3 算例验证

3.1 算例1

选取文献[8]中的二元非线性功能函数作为研究对象，其表达式为

(29)

式中，x1～N(0,1)，x2～N(0,1)，且相互独立.

初始LHS训练样本点设置为6个，并采用106个MC样本点计算该二元函数的失效概率.由不同真实失效样本数Nf取值范围的估计方法及相应停止条件得到的可靠性分析结果如表1所示，其中Ncall为功能函数调用次数.显然，本文的可靠性分析方法在满足精度要求的同时，比其他方法需要更少的功能函数调用次数.

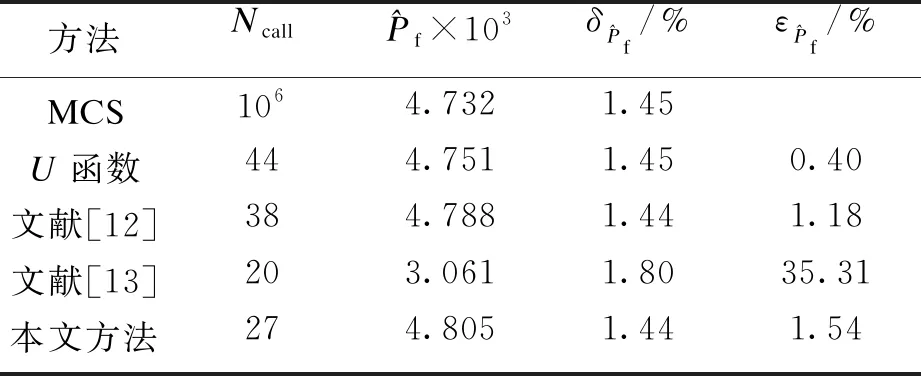
表1 不同方法的分析结果Table 1 Results of different methods

3.2 算例2

以图3所示的具有9个随机变量的悬臂式管结构[14]为分析对象，其功能函数为结构屈服强度S和最大应力σmax之差，即

G(t,d,L1,L2,F1,F2,P,T,S)=S-σmax.

(30)

式中各随机变量的分布特征如表2所示，σmax为原点处悬臂管上表面所受的最大等效应力：

(31)

式中

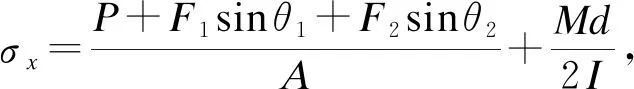
表2 各随机变量的分布特征
Table 2 Distribution of random variables

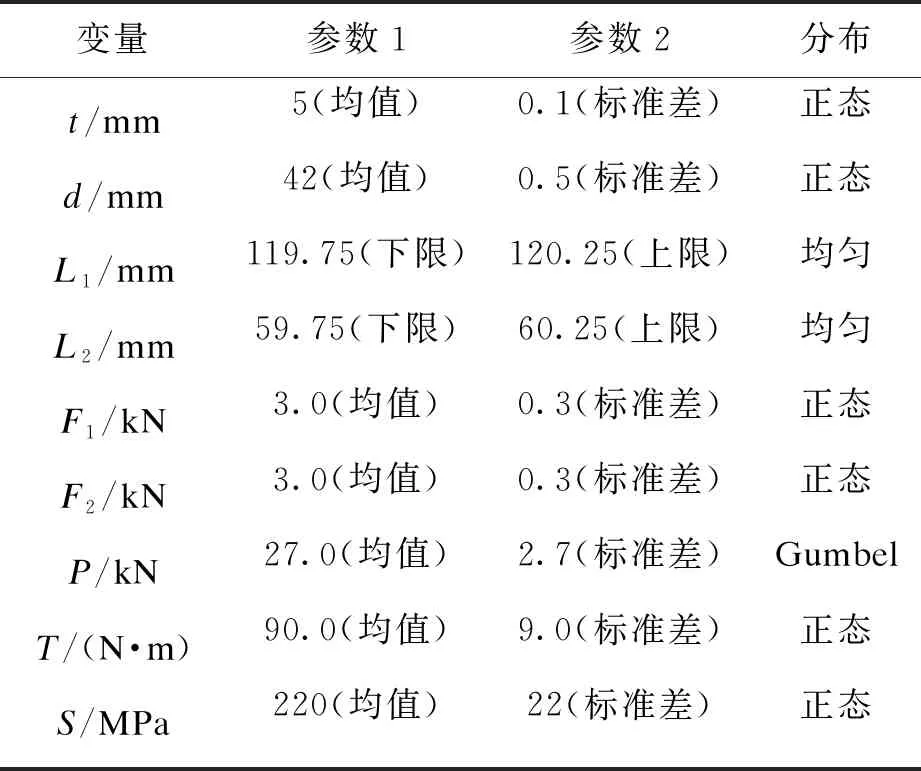
变量参数1参数2分布t/mm5(均值)0.1(标准差)正态d/mm42(均值)0.5(标准差)正态L1/mm119.75(下限)120.25(上限)均匀L2/mm59.75(下限)60.25(上限)均匀F1/kN3.0(均值)0.3(标准差)正态F2/kN3.0(均值)0.3(标准差)正态P/kN27.0(均值)2.7(标准差)GumbelT/(N·m)90.0(均值)9.0(标准差)正态S/MPa220(均值)22(标准差)正态

初始LHS训练样本点设置为12个，并采用2.0×105个MC样本点计算该悬臂管的失效概率.表3和图4列举了采用不同方法得到的结果.相较于其他方法，在满足可靠性分析精度要求时，本文方法在效率上更具优势.

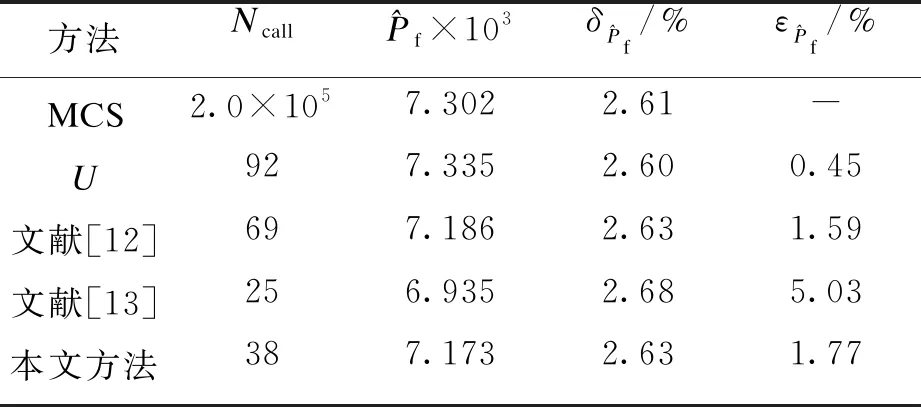
表3 不同方法的分析结果Table 3 Results of different methods

4 结 论

1) 通过两个算例表明，本文确定的取值区间不仅能够准确地包含真实失效样本数，而且还能得到更精确的失效概率相对误差估计结果.

2) 本文提出的基于失效概率相对误差估计的自适应可靠性分析方法在满足分析精度要求的同时极大地减少了功能函数的调用次数，为解决实际工程中复杂结构的可靠性问题提供了一种切实可行的分析方法.