基于方向分数和Frangi滤波器的视网膜血管分割算法

佘黎煌, 郭一蓉, 张 石

(东北大学 计算机科学与工程学院, 辽宁 沈阳 110169)

视网膜血管是人体血管系统中唯一可以非创伤直接观察到的深层血管,其形态结构的变化直接反映心脑血管等疾病的病程,可作为与血管相关疾病的诊断依据[1].借助计算机对眼底血管图像进行分割,有助于对眼科疾病进行辅助诊断,是国内外学者研究的热点.

视网膜血管分割方法分为两类:基于像素分类法[2]和基于血管追踪法[3].本文主要对基于血管追踪法进行研究和改进.

血管追踪过程中图像的分岔、交叉会导致分割结果不理想,因此本文提出一种基于方向分数和Franqi滤波器相结合的视网膜血管分割算法.由Hessian矩阵构造的Frangi滤波器具有 Hessian矩阵对线状物体优良的滤波效果,因此对血管进行滤波可以突出血管和背景的区别,但滤波器的高斯卷积处理会导致分割结果在血管交叉处相连;鉴于此,将Frangi滤波器和方向分数结合进行血管分割.方向分数可以在二维平面的基础上,再添加一个角度的维度,这样可以将二维图像中的细长结构映射到不同平面进行处理,并且不篡改数据.本文中的方向分数由文献[4]提出的蛋糕小波构成,该小波的各向异性可以捕获所有图像尺度且不会对特定尺度产生误差,同时正交性可以确保不丢失信息.实验表明,本文算法可以很好地处理分岔问题,也有良好的准确度、灵敏度等.

1 基本原理

Frangi滤波器[5]基于Hessian矩阵特征值来增强血管对比度,可以抑制非血管结构.

方向分数是通过将一幅二维图像提升到旋转平移群SE(2)=R2×S1上的三维函数来实现的.一个2D图像f可以通过一个各向异性的小波变换wψ来构建方向分数Uf:=wψf,具体表示为

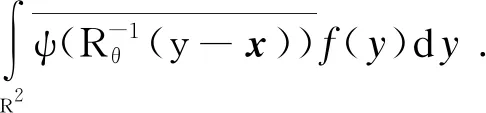
(1)

式中:x=(x1,x2)表示位置;θ∈[0,2π]表示方向范围;ψ∈L2(R2)表示与水平轴对称且与垂直轴对齐的方向θ=0的卷积小波核;Rθ表示旋转矩阵:

(2)

经方向分数处理过的图像可以重新回到2D图像,即

(3)

(4)

卷积小波核在空间域表示为

(5)

(6)

式中:ω=(ρcosφ,ρsinφ)为傅里叶域的极坐标;sθ=2πN-1为弧度的角分辨率;Bk为k阶B样条函数,k值取2:

(7)

MN为傅里叶域的径向函数,本质是一个标度为t的高斯函数与其导数的泰勒级数相乘,以确保缓慢衰减：

(8)

2 算法实现

本文算法是先提取原始彩色图像的绿色通道,然后对预处理之后的图像进行顶帽变换等增强操作;随后根据Frangi滤波对血管的敏感性进行滤波处理,进而与蛋糕小波卷积,利用蛋糕小波的各向异性和正交性构造可以多方向、多角度增强血管的方向分数,便于后续血管网络的提取;最后通过阈值分割获得血管网络结构.

2.1 预处理

本文范例选取DRIVE[6]数据库中的图像进行算法验证.通过实验得知,在图像的3个分量中,绿色通道的对比度最大,故选择绿色通道图像,如图1a所示.

对提取的绿色通道图像进行顶帽变换,得到图1b所示结果.可以看出,图像保留了需要分割的重要信息,获得了更多图像细节.

2.2 图像增强

为了更好地分割血管,提高图像的对比度,采用灰度拉伸灵活控制输出灰度直方图的分布：选择性地拉伸某段灰度区间来达到增强图像对比度的效果,如图2a所示.对图像边缘出现的类似反射的不正常现象,采用阴影校正方法修正,结果如图2b所示.

2.3 血管增强

实际应用时,由于二阶偏导数对噪声比较敏感,一般会在求Hessian矩阵前进行高斯平滑,即

(9)

式中:I表示图像;Gδ(x,y)表示尺度为δ的二维高斯函数.应用卷积的交换律,将式(9)变为先求高斯二阶微分,再与图像进行卷积,即

(10)

在描述血管信息时,图像的血管是管状细长结构,高斯二阶导数的响应值较大;背景部分是均匀部分,响应值较小.因此,血管点处的特征值是一大一小,背景点处的特征值是两个都小,而交叉点处的特征值是两个都大.Frangi滤波器是利用Hessian矩阵特征值在图像上的这种特点构造出来的边缘检测滤波器.本文中,血管图像经过Frangi滤波器滤波之后的结果如图3a所示.

由图3a可见,滤波器确实在一定程度上强化了线状物体的对比度,但同时也丢失了许多细节信息.为了提取更多的血管细节信息,提高血管增强在随机图像上的效果,经Frangi滤波器处理后的图像与蛋糕小波卷积,进入方向分数域进行处理.方向分数是通过图像与一个具有方向性的小波卷积得到的,这个构建过程可以实现傅里叶域中的小波分层,从而实现将图像从二维平面提升到三维空间.小波核可以选择Gabor小波和蛋糕小波,但Gabor滤波器在空间域存在分层数量增加时频率重合的问题,容易造成图像信息的冗余;因此,本文选择蛋糕小波作为构建方向分数的小波核.本文中的范例图像经过方向分数变换之后的结果如图3b所示,可以看出图像细节信息增加,血管对比度明显提高.

2.4 血管分割

将增强后的图像用阈值分割,得到如图4a所示的视网膜血管网络,再将图像和掩膜图像进行按位“与”操作,去掉边缘,得到最终结果,如图4b所示.

3 实验结果及分析

3.1 实验数据

目前常用的公开的彩色眼底图像数据库主要有DRIVE,SRARE[7]和Review[8]等,可以利用这些数据库比较相关算法的有效性.本文选取最常用的DRIVE,SRARE数据库作为测试算法的数据.

3.2 实验结果评价指标

本文选取认可度较高的像素点分类方法对血管分割方法进行性能评估,该标准是将算法分割结果和专家标准分割结果作比较.像素点的统计有4种情况:真阳性(TP)表示正确分割为血管的点数;假阳性(FP)表示被错误分割的血管点数;真阴性(TN)表示正确分割为背景的点数;假阴性(FN)表示被错误分割的背景点数[9].可以通过像素点分类结果计算出准确率(Acc)、灵敏度(Sn)、特异度(Sp).准确率表示分割正确的像素点数占整体像素点数的比率,灵敏度表示分割正确的血管点数占像素点数的比率,特异度表示分割正确的背景点数占像素点数的比率.具体计算方法如下:

(11)

(12)

(13)

数值越接近1表示算法的性能越好.

3.3 仿真结果

为了验证本文算法的综合性能,分别对DRIVE和STARE数据库中的图像进行测试.

图5为本文算法在DRIVE数据库和STARE数据库中的测试结果,其中第一列和第三列为专家人工分割的标准结果,第二列和第四列为本文算法分割结果,每行是从数据库中选取的不同图像.

由以上结果可以看出,本文提出的视网膜分割算法能够较好地分割出视网膜眼底图像的血管网络,且具有较好的完整性和连贯性,对血管点和非血管点都有不错的分割结果.

将本文算法与基于高斯微分的分割算法[10]和基于改进Hessian矩阵的分割算法进行对比分析,结果见图6和图7.

图6是用DRIVE数据库中的图像进行对比,可以看出,基于高斯微分的方法只可以保留血管网络的大致主体,细节部分丢失严重,也存在血管断裂的情况;基于改进Hessian矩阵的方法分割效果有明显提升,血管断裂情况得到改善,但是在血管分岔处的分割效果还是不理想;本文算法除了可以分割出完整的血管网络,也较好地完成了血管分岔处的分割.

图7是用STARE数据库中的图像进行对比,可以看出,与其他算法相比,本文算法除了可以分割出完整的血管网络,也可以保留血管的细节信息.

表1是本文算法针对DRIVE和STARE两个数据库中图像的3个分割性能指标计算结果.从表中可以看出,算法在DRIVE数据库中的平均准确率为0.959 3,灵敏度为0.738 7,特异度为0.980 2;在STARE数据库中的平均准确率为0.942 5,灵敏度为0.747 6,特异度为0.956 3.算法在两个数据库中均有较高的分割准确率、灵敏度和特异度,具有较好的分割性能.

同时,本文还计算了基于改进Hessian矩阵的分割方法、基于高斯微分的分割方法及文献[10]提出的方法在两个数据库中的分割准确率、灵敏度和特异度,并与本文算法进行比较,结果见表2. 结合表中的数据可以看出,本文算法针对DRIVE数据库中的图像，在分割准确度、灵敏度和特异度上都有不错的效果,尤其是准确度和特异度；在STARE数据库中也取得了较好结果.

表1 本文算法测试结果Table 1 Test results of the algorithm proposed

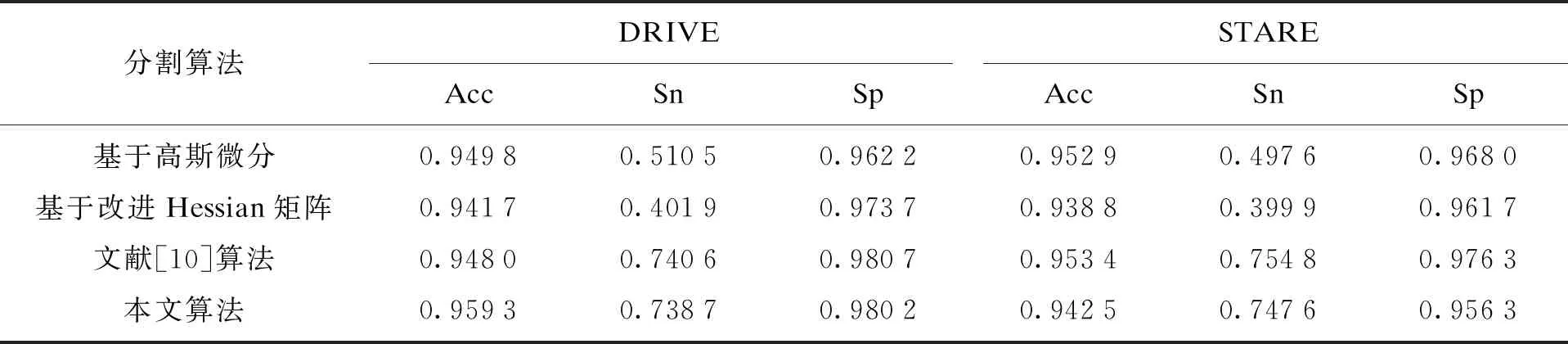
表2 算法性能比较Table 2 Comparison of algorithm performance

4 结 语

本文在分析现有视网膜分割算法的基础上,将近几年分割效果好的方向分数和Frangi滤波器结合,提出新的改进算法.Franqi滤波器可以利用Hessian矩阵有利于线状物体平滑的特点提高血管图像对比度；而高斯卷积带来的血管交叉处易相连问题,则通过方向分数得到改善.方向分数可以通过高斯二阶偏导数很好地实现多方向、多角度的滤波,为后续分割提供良好基础.将本文算法在DRIVE和STARE数据库中的测试结果与标准结果进行对比,表明本文算法可以很好地处理血管分割过程中出现的交叉和分岔现象,同时也可以保证较高的准确率、灵敏度和特异度,总体分割效果优于现有算法.