地震荷载和列车荷载共同作用下弹性均质路基的动力响应

，高盟

(1.山东科技大学 土木建筑学院，山东 青岛 266590； 2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590； 3.新加坡国立大学 土木与环境工程系， 新加坡 119077)

近年来，我国高速铁路建设加速，线路密集、发车时间间隔短，加上我国又是地震多发国家，导致地震发生时，高速列车在轨运行机率大大增加，列车脱轨风险增大。高速铁路地震预警预报系统是解决高速铁路抗震的直接措施，如日本新干线采用监测P波和S波的方式进行预警预报；我国的京沪高铁也建立了地震监控系统。由于地震预警预报系统不能识别地震和其他振源产生的振动，导致时常发生列车自动停车，造成列车延误等事故。因此，从岩土工程的角度研究地震荷载作用下列车在轨运行引起的路基的振动响应规律对高速铁路抗震减震具有重要意义。

已有研究成果往往重视车-轨相互作用，研究地震荷载作用下车-轨的动力接触力学机制，分析列车脱轨的力学因素，而忽略地基的影响。如Ling等[1]以35自由度多体系统模拟列车，以离散弹性支承模型模拟轨道研究地震作用下列车脱轨的力学机制。Tanabe等[2]将列车看作非线性弹簧支承在弹塑性轨道的多体动力模型，对地震过程中车-轨动力相互作用进行分析。Ju等[3]用时域有限元法模拟地震荷载作用下列车脱轨，分析列车脱轨的影响因素。Luo[4]提出一个简化解析模型评估地震作用下列车的动力反应。Hall[5]用数学数值模型分析地震作用下列车的振动数据，发现在路堤和路堤下方的软土层中存在相对较大的剪切应力。Xiang等[6]利用系统动力稳定概念描述列车脱轨的力学机制，提出列车脱轨的随机分析理论。Nishimura等[7]通过人工地震输入对列车的脱轨力学机制进行试验研究。

上述文献大多分析列车运行速度对脱轨的影响，但得出的结论并不一致，如Ling等[1]认为地震作用下列车速度对脱轨的影响不明显，而Ju等[3]认为在完全规则平顺轨道上，列车速度与脱轨无相关性，而不规则轨道列车速度对脱轨影响巨大。事实上，影响列车脱轨的因素不仅有列车和轨道系统，路基结构及地基条件也是影响列车在地震中脱轨的重要因素[8-9]，不同的路基结构和地基条件对高铁列车的抗震减震的影响显然不同。目前国内外学者对单一列车荷载作用下铁路隧道的路基结构做了初步研究与探讨，取得了一定的研究成果，但对地震荷载和列车荷载共同作用下的路基结构动力响应特征的研究鲜有报道。

因此，建立了地震荷载和列车移动荷载共同作用下的三维ABAQUS数值计算模型，分析地震荷载和列车荷载共同作用下路基结构在不同列车速度、轴重、沿路基横向和深度方向等因素的动力响应问题。研究成果对地震荷载和列车移动荷载共同作用下路基的动力响应提供重要参考。

1 计算模型及参数

1.1 有限元模型的建立

依据《高速铁路设计规范》[10]建立轨道结构-路基-地基三维有限元模型，如图1所示。系统由钢轨-扣件-轨道板-CA砂浆层-底板-基床表层-基床底层-路基本体-地基组成。模型沿线路纵向的长度为52 m，地基表面宽度为52 m，总高度为25.456 m。钢轨采用60 kg·m-1标准钢轨，轨距为1.435 m，扣件支点间距为0.65 m。钢轨与扣件之间采用弹簧阻尼器进行模拟，扣件刚度和阻尼系数[11]中等效刚度沿横向、垂向、纵向分别为37.5、25和37.5 kN·m-1，阻尼系数分别为30、37.5和30 kN·s·m-1。轨道板、CA砂浆层、路基和地基均采用8结点实体单元。由于轨道板与基床表面、路基本体底面与土体之间的滑动相对较小，不考虑各接触面之间的摩擦，通过Tie接触[12]保持各接触面之间的变形协调。地基四个侧面采用黏弹性边界，模拟波从有限域向无限域传播。钢轨网格划分尺寸为 0.05 m，钢轨共22 880个单元，模型共65 624个单元，总节点数为81 164个，单元类型均为C3D8R。

图1 有限元计算模型Fig. 1 Finite element computing model

1.2 模型计算参数

有限元模型由钢轨-扣件-轨道板-CA砂浆层-底板-基床表层-基床底层-路基本体-地基组成。参考文献[13]，计算模型各组成部分采用弹性本构。动力学问题分析必须考虑阻尼的影响，通过对有限元模型进行自身特征值分析，计算获取系统第一阶和第二阶自振频率分别为2.15 98和2.193 4 Hz，参照文献[14]中的阻尼比进行模型瑞利阻尼计算，结果见表1。

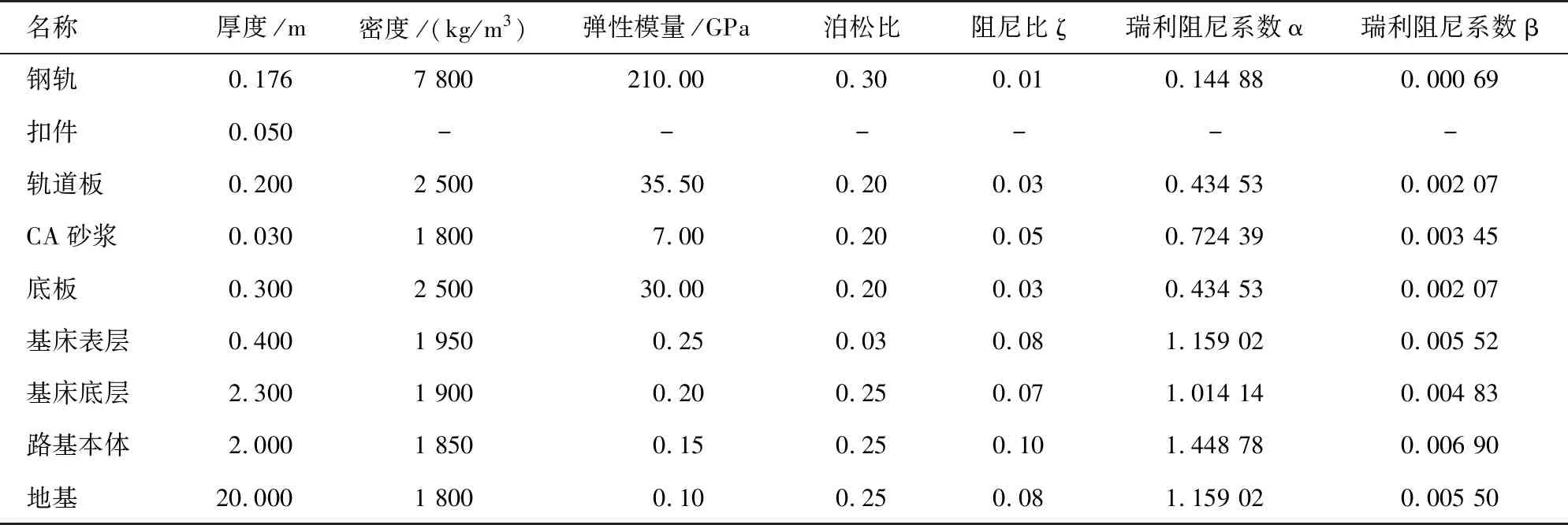
表1 有限元模型计算参数

1.3 列车荷载

列车运行中轨道上所受的列车动荷载包括三部分：移动的动荷载、固定作用点的动荷载、移动的轴荷载[15]。为着重研究路基的动力响应问题，忽略轮轨接触不平顺等引起的影响，只考虑列车竖向荷载作用。通过编制的DLOAD子程序将列车移动荷载与ABAQUS程序联立，实现列车荷载的施加。列车由多组连续轴重荷载模拟，采用边学成等[16]给出的关系式：

(1)

式中：M表示车厢节数，列车速度为c，右式表示第n节车厢轴重在移动时对钢轨产生的竖向荷载。fn的具体表达式为：

(2)

式中：Pn1和Pn2分别表示车厢前轮和后轮的轴重；Ls为车厢的长度；L0是从第1节车厢前某一个设定的测量点开始的距离；an、bn为轴之间的距离；δ(·)是表示冲击荷载的Dirac函数。

列车选用CRH3型动车组，动车组长度约200 m，列车轴重为17 t，中间车车辆长度为25 m，车辆定距为17.375 m，转向架的固定轴距为2.5 m，两辆车之间轴距为4.5 m。在数值仿真模拟中，由于几何尺寸受到计算机性能的限制，并不能将整列车完全模拟出来。列车移动荷载选取多轴模型中最不利的激励形式，选用两个相邻车辆的端部转向架的四个轮对。列车荷载示意图如图2所示，其中Pi1、Pi2、Pi3和Pi4分别代表车厢前后轮的轴重。选取P13、P14、P21和P22四个轴重荷载模拟列车荷载，分析列车荷载和地震荷载共同作用下路基的动力响应。

图2 列车轴重荷载分布图Fig. 2 Distribution of train axle loads

1.4 地震荷载

在计算结构的地震响应时，较合理的方法是将地震波动转化为边界结点上的等效荷载。夏栋舟等[17]在计算结构抗震性能分析时，将地震波加速度直接从模型底部输入，得到了合理的结果，本研究亦采用此方法。输入Imperial Vally地震波，将地震波峰值调整至0.1g，其水平方向加速度时程曲线如图3所示。取地震加速度时程曲线2～3.6 s加速度从模型底部输入，经计算此时地面的加速度峰值约为0.13g，相当于烈度为7度的地震。

图3 Imperial Vally 地震加速度时程曲线Fig. 3 Acceleration time history of Imperial Vally

2 计算结果分析

有限元分析大多对实际情况进行适当简化，以便进行模拟计算，而模型建立的合理与否会直接影响计算精度和运算时长。因此，为保证研究结果的准确性，首先对模型计算的准确性及精度进行验证，然后基于准确的数值模型进行计算，对所得结果进行分析，总结地震荷载和列车荷载共同作用下弹性均质路基的动力响应规律。

2.1 数值模型及分析方法的有效性验证

董亮等[18]选取CRH2动车组中一个转向架荷载，对高速铁路无砟轨道路基结构的基床表层顶面竖向动应力进行实测和数值模拟。如图4所示，采用相同材料参数及列车轴重，得到了基床表层竖向动应力对比图。比较可知，数值模拟的基床表层动应力时程曲线和文献[18]结果基本吻合，故计算模型在分析路基结构的动应力和动位移方面是合理有效的。

2.2 地震荷载和移动荷载共同作用下路基动力响应分析

2.2.1 路基位移分析

由图5可知，在单独地震荷载作用时，基床表层和基床底层的位移时程曲线几乎相等，路基本体的位移要小于基床表层和基床底层，位移从下往上有一个放大的趋势。提取1.33 s时的路基各结构层位移进行分析，施加列车移动荷载后，路基各结构层的位移明显较小，对基床表层的影响最大，最大变化量为0.23 mm；基床底层的变化量为0.22 mm；路基本体的变化量为0.18 mm。各参考点在1.33 s时的变化率见表2。

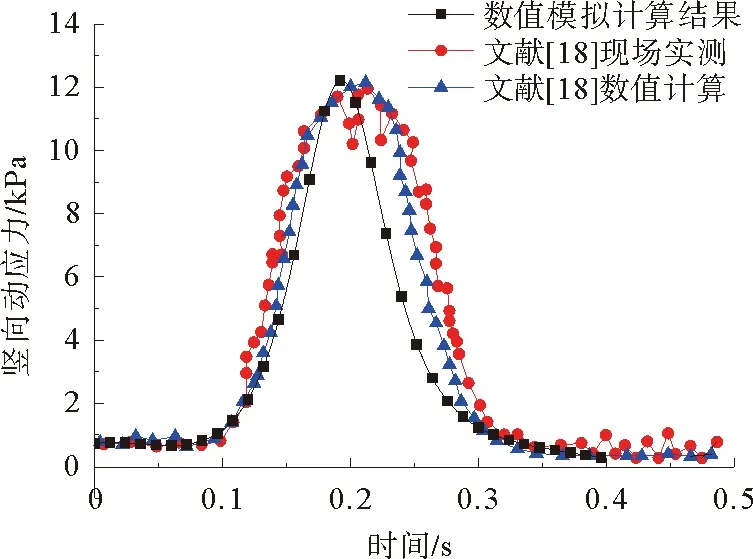
图4 基床表层顶面竖向动应力时程曲线Fig. 4 Time histories of vertical dynamic stress for slab track subgrade surface

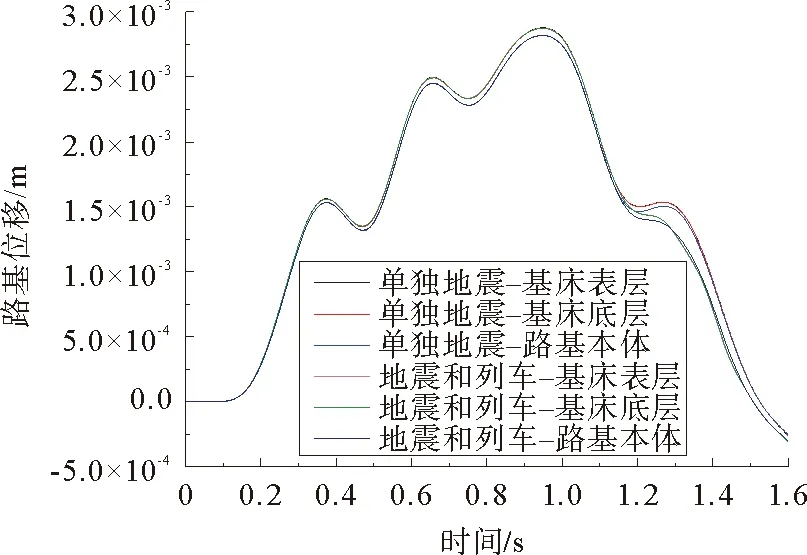
图5 路基各结构层竖向位移时程曲线Fig. 5 Time histories of vertical displacement for structural layers of subgrade

表2 路基不同参考点位移变化率

由图6和表2可知，距轨道中心越近，基床表层竖向位移越大，且从轨道板边缘1.3 m处到底板边缘1.6 m处竖向位移衰减最快。从图7可以看出，从基床表层向下，各参考点的竖向位移逐渐减小。基床表层0～0.4 m位移衰减较快，基床底层0.4～2.7 m衰减最慢，路基本体2.7～4.7 m位移衰减最快。

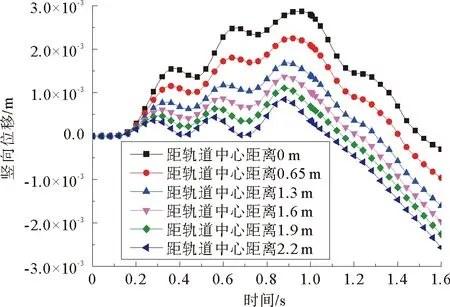
图6 距轨道中心不同距离的基床表层位移Fig. 6 Displacement of subgrade surface at different distances

图7 路基竖向位移沿深度变化Fig. 7 Displacement of subgrade along the depth

2.2.2 路基各结构层加速度分析

图8中，0～1 s为单独地震荷载作用，1 s后开始施加列车移动荷载。由图可知，地震荷载路基各结构层的影响非常小，加速度主要受列车荷载影响。基床表层加速度最大，最大值为10.32 m/s2，基床底层最大值为7.39 m/s2，路基本体最大值为0.66 m/s2。其中在路基各结构层中，从基床表层到路基本体受地震荷载的影响逐渐增大，受列车荷载的影响迅速减小。路基各结构层的主导频率也为125～160 Hz，路基本体受地震荷载影响较大，在低频0～20 Hz区间出现了一个峰值。基床表层和地层受地震荷载影响较小，没有出现地震荷载影响的主频。

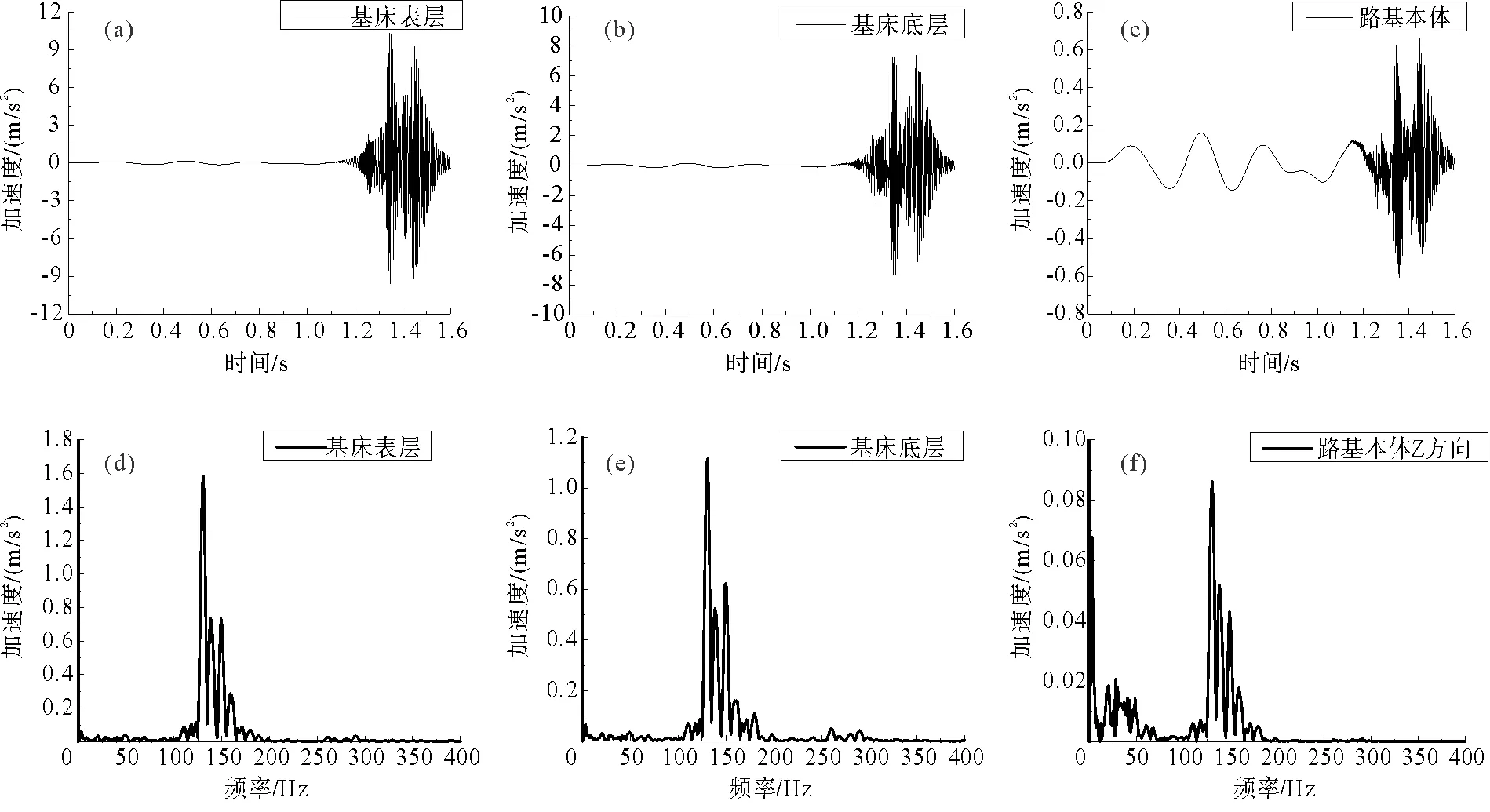
图8 路基各结构层加速度时程和频谱曲线Fig. 8 Acceleration time history and spectrum curves of subgrade structural layers

由图9可以看出在距轨道中心0～0.65 m时，加速度衰减较慢；0.65～1.3 m，加速度衰减逐渐增大；1.3～1.6 m加速度迅速减小，衰减速度较快；1.6～2.2 m加速度衰减由逐渐稳定，逐步接近线性衰减。其中，基床表层0～1.3 m处位于轨道板和底板下方，0～1.6 m处位于底板下方。

由图10可知，加速度沿深度方向衰减速度逐渐减小，衰减曲线近似为抛物线。0～2.7 m加速度衰减速度较快，其中0～0.4 m为基床表层，0.4～2.7 m为基床底层。由此可知，路基中的基床表层和基床底层对上部结构的振动有较好的减震作用。

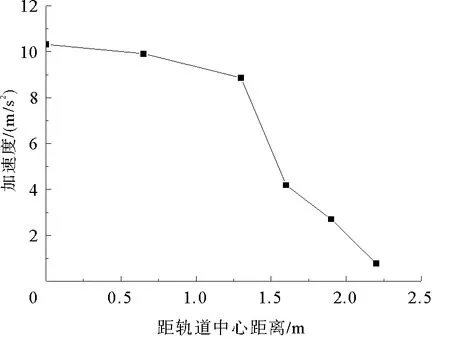
图9 距轨道中心不同距离基床表层加速度Fig. 9 Acceleration of subgrade surface at different distances

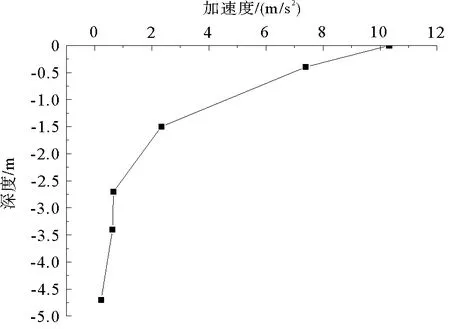
图10 路基加速度沿深度变化Fig. 10 Acceleration of subgrade along the depth

2.2.3 路基动应力分布

确定路基内动应力分布是分析路基沉降变形和稳定性的重要前提。

图11给出的是在0.1g地震加速度和70 m/s列车荷载作用下距轨道中心点处不同距离的基床表层动应力变化图。由图可知，0～1 s内，仅施加地震荷载作用下，基床表层动应力随着时间推移逐渐增加，但增加的幅度略有不同。增长幅度较大的是距离轨道中心1.3 、1.6 和1.9 m位置处，其峰值应力分别为2.5、4.0和3.2 kPa；相对幅度较小的是距离轨道中心0、0.65和2.2 m处，其峰值应力为0.72、0.65和0.3 kPa。最大峰值应力是最小峰值应力的13.3倍，相差约3.7 kPa。1 s后，开始施加列车荷载，基床动应力迅速衰减，反向依次达到两个峰值后，再次衰减为0。其中，所达到的最大峰值应力为22.4 kPa(距轨道中心1.6 m)，是最小峰值应力0.7 kPa(距离轨道中心2.2 m)的32倍，是仅施加地震荷载的最大峰值应力的5.6倍，这表明了列车移动荷载在路基动应力中发挥主导作用。此外，两次正反动应力的最大值均出现在距离轨道中心1.6 m的位置，这是因为此处为轨道板边缘正下方，所以基床表面应力从轨道中心向轨道板边缘逐渐增大，至边缘后衰减，这也与路基结构的横向动应力云图变化规律保持一致。

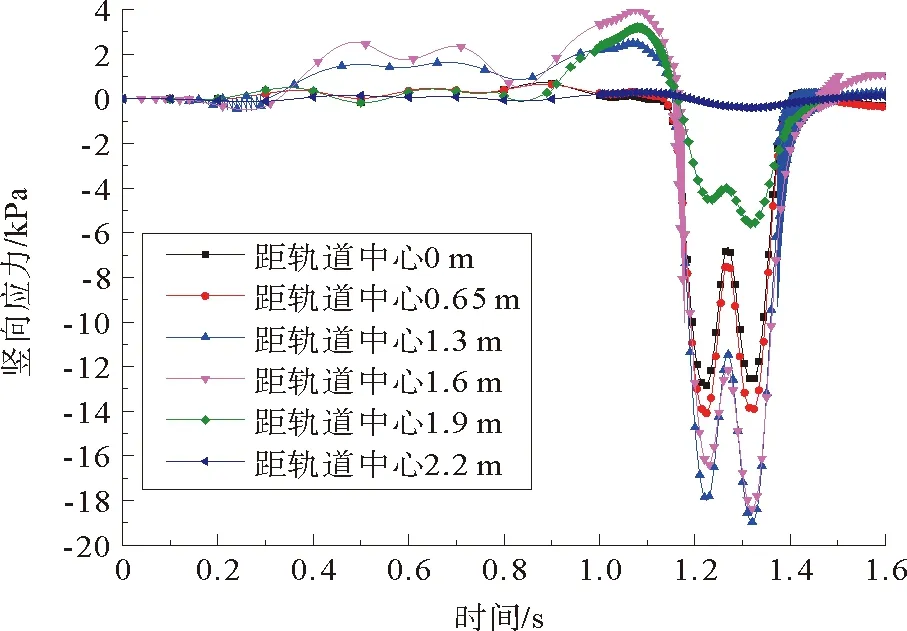
图11 距轨道中心不同距离基床表层动应力Fig. 11 Dynamic stress of subgrade at different distances

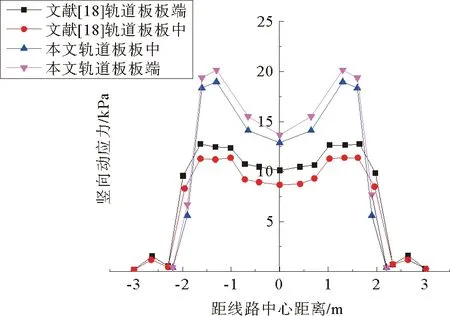
图12 基床表层顶面横断面竖向动应力分布Fig. 12 Dynamic stress distribution on subgrade surface

为了进一步探讨列车移动荷载和地震荷载共同作用下的动应力分布情况，选用文献[18]中仅施加移动荷载的基床表层横断面竖向动应力分布的计算结果做对比，得到了图12的对比分布图。由图可知，列车荷载和地震荷载共同作用下的计算结果与文献[18]一致，即基床表层动应力分布变化趋势一致：动应力在钢轨正下方最大，在轨枕两端部和线路中心位置相对较小，沿横向呈“马鞍型”分布。列车移动荷载和地震荷载共同作用下的计算结果比仅施加移动荷载的结果偏大一些，约1.7倍。主要原因是，共同作用时列车轴重为17 t，列车速度为70 m/s，而文献[18]中采用的列车轴重为14 t，列车速度为44 m/s。此外，二者的变化趋势基本一致，也再次证明地震荷载对基床表层动应力影响较小，主要表现为列车荷载对基床的影响。

图13为在0.1g地震加速度和70 m/s列车荷载作用下在轨道中心点处，以到路基基床表面的距离为变量，研究沿深度方向的路基动应力变化情况。0～1 s为单一地震荷载作用下路基的动应力，可以发现随着深度增大，路基动应力略有增加，但6条动应力曲线相差不明显。例如，最小的动应力峰值是基床表层顶面中心点处，约为0.24 kPa，最大为距离表面最深处(4.7 m位置)，约为1.21 kPa，相差不足1 kPa。1～1.6 s为地震荷载和列车移动荷载共同作用，但可以看出列车移动荷载对路基动应力起主导作用。此外，分析发现6条不同深度的曲线的竖向应力峰值各不相同，但其变化规律基本一致，即竖向动应力沿着深度方向逐渐减少。基床表面动应力最大为13.2 kPa，沿深度方向延伸，动应力在距基床表层4.7 m处仅有4.3 kPa，衰减了67.8%。

图14为列车移动荷载和地震荷载共同作用与仅施加移动荷载的基床表层基床动应力沿深度变化的计算结果对比图。由图可知，列车荷载和地震荷载共同作用下的计算结果与文献[18]中仅施加移动荷载中钢轨下方的变化趋势相似：路基结构的动应力沿深度方向不断衰减，且衰减速率逐渐加快。但计算结果比文献[18]中结果偏大，主要是因为采用的列车轴重和列车速度均比文献[18]中要大。说明地震荷载对基床表层动应力影响较小，主要表现为列车荷载对基床的影响。

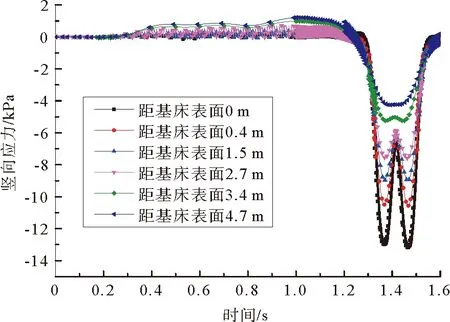
图13 路基竖向动应力沿深度变化Fig. 13 Stress variation of subgrade along the depth

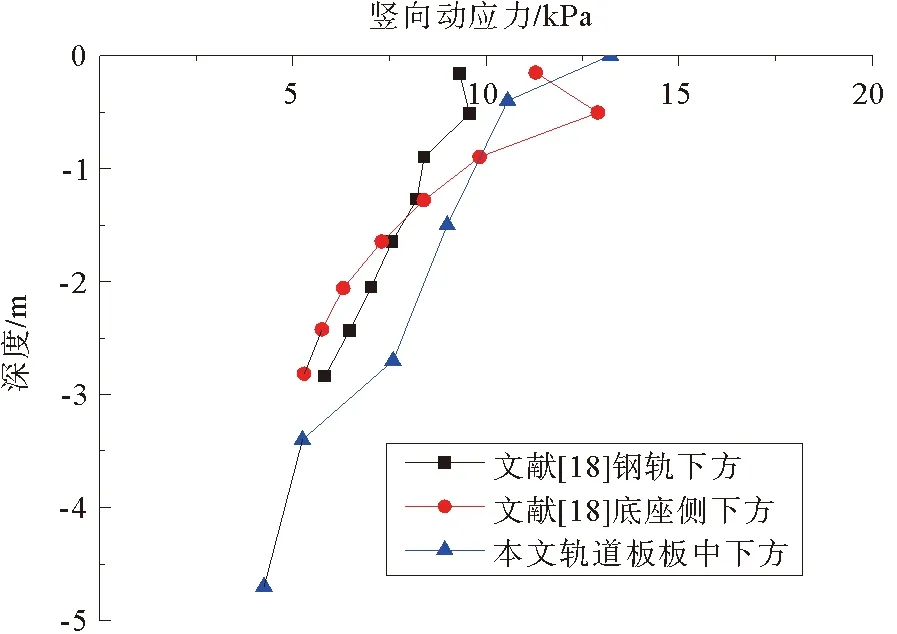
图14 基床动应力沿深度变化Fig. 14 Stress variation of subgrade along the depth

2.2.4 列车轴重对路基动力响应的影响

为了分析列车轴重对振动的影响，选取地震加速度为0.1g，列车速度为70 m/s，列车轴重分别为17、20、23和26 t进行模拟，选取路基各结构层的位移和加速度进行分析。

由图15可知，路基各结构层的位移随着列车轴重的增加而减小，其中列车荷载对基床表层和基床底层影响较大，随着列车轴重的增加路基各结构层位移的衰减速度越来越大。

由图16可知，路基各结构层加速度随着列车轴重的增加而增加。其中，列车轴重从17 t增加到20 t时，基床表层加速度增大了2.77 m/s2。从20 t增加到23 t时，基床表层加速度增大了1.85 m/s2。从23 t增加到26 t，基床表层加速度增大了2.11 m/s2。基床表层加速度变化率表现为先增大后减小又增大的趋势，基床底层变化趋势和基床表层一致，列车轴重对路基本体影响较小。

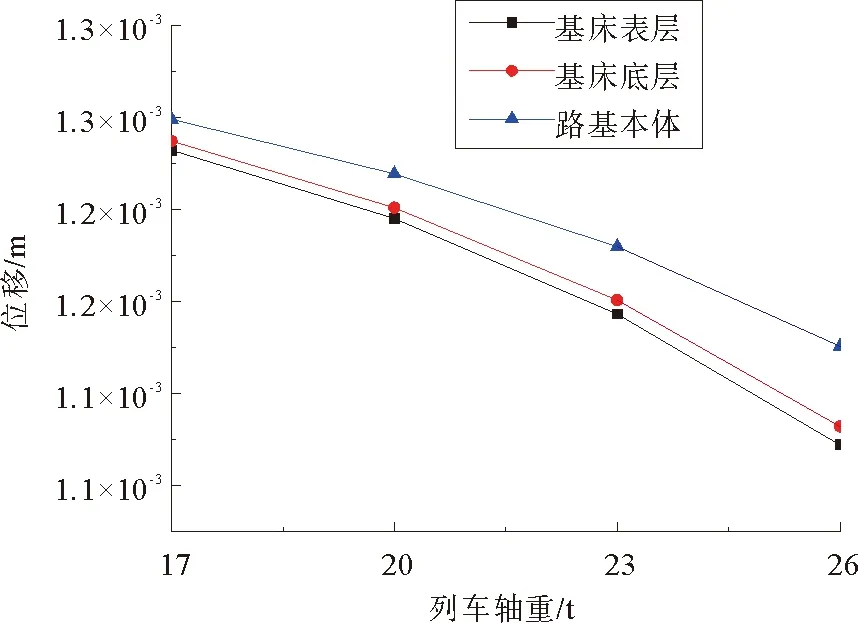
图15 路基各结构层位移随轴重变化Fig. 15 Displacement variation with train axle loads

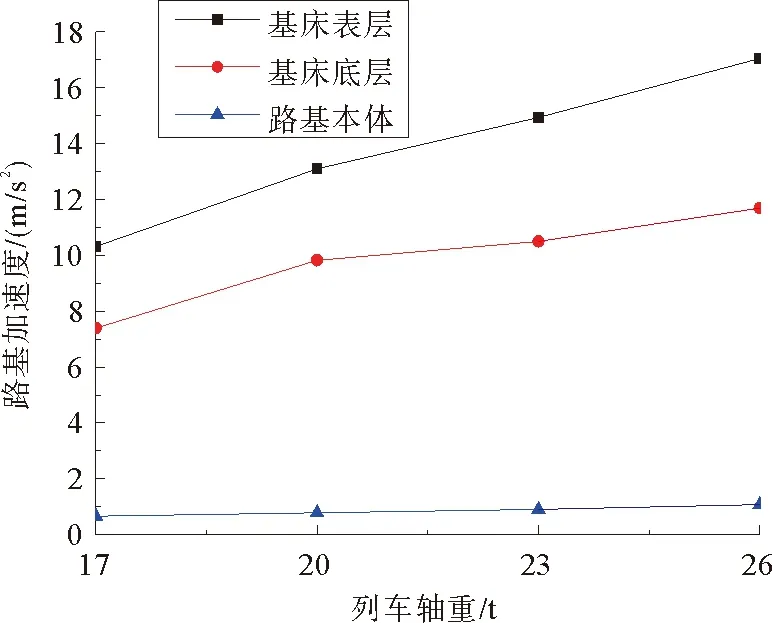
图16 路基各结构层加速度随列车轴重变化Fig. 16 Acceleration variation with train axle loads

2.2.5 列车运行速度对路基动力响应的影响

由于选取的参考点是一致的，列车车速不同，导致列车到达参考点的时间是不同的，所以不同时间的地震加速度也是不同的。因为列车车速和地震加速度都不一致，两个变量无法直接比较。因此，先比较路基位移随列车车速变化曲线与单独地震作用时的位移曲线，得出不同列车速度对路基位移影响的最大值，然后再进行比较，如表3所示。由表3可知，路基各结构层的位移从基床表层到路基本体逐渐减小，且随着车速增加变现为先减小后增大的趋势，在列车车速为70 m/s时，路基各结构层的位移达到最小值。但是在列车车速到达70 m/s以上时，基床表层和基床底层的位移大小相同。列车车速对路基位移的影响呈现从30～70 m/s逐渐减小，70 m/s以上逐渐增大的趋势。

表3 不同列车车速路基位移

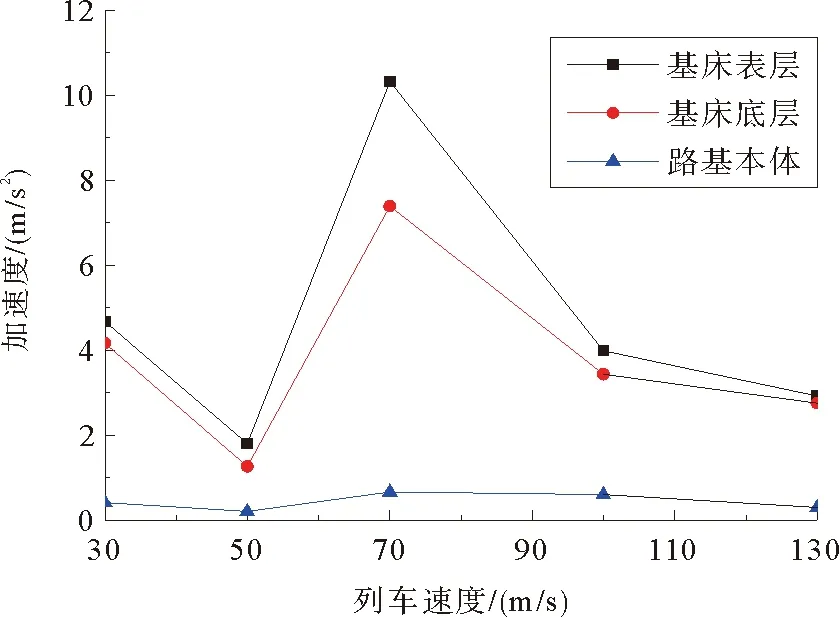
图17 路基各结构层加速度随列车速度变化Fig. 17 Acceleration variations of subgrade structural layers with different train speeds

由图17可知，路基各结构层的振动加速度表现为先减小后增大又减小的趋势。其中基床各结构层在列车车速为50 m/s时达到最小值，在车速提高到70 m/s时振动加速度迅速增大，达到最大值，之后又逐渐减小。综上分析可知，在列车车速为70 m/s时路基位移最小，加速度最大，推测车速70 m/s为临界速度。

3 结论

利用ABAQUS和FORTRAN相结合的方法，建立了高速铁路无砟轨道-路基-地基三维数值分析模型，对高速铁路路基在地震荷载和列车移动荷载作用下的应力和位移进行了分析研究。主要研究结论如下：

1) 路基位移主要受地震荷载影响，从下往上有一个放大的趋势；路基各结构层的加速度主要受列车荷载影响，从上向下加速度迅速衰减；路基动应力主要受列车荷载影响，路基动应力沿横向呈“马鞍型”分布，沿纵向近似“抛物线”分布。

2) 路基各结构层的位移随着列车轴重的增加而减小，随着车速增加表现为先减小后增大；路基各结构层加速度随着列车轴重的增加而增加，随着车速增加表现为先减小后增大又减小的趋势。

3) 在列车车速为70 m/s时，路基各结构层的主导频率为125～160 Hz，路基本体受地震荷载影响较大，在低频0～20 Hz区间出现了一个峰值；路基位移最小，加速度最大，因此推测车速70 m/s为临界速度。