对某中小型危化企业安全投资—效益关系模型的研究

王文立， 李亚斐， 张乐

(1. 中国平煤神马集团河南神马氯碱化工股份有限公司，河南 平顶山 467200；2.河南省平顶山市新华区香山街小学，河南 平顶山 467047)

化工企业是以物料的合成、反应得到新的生成物为基础的企业，在我国国民经济生产中具有十分重要的作用。但是鉴于化工生产具有高温、高压、易燃易爆且有毒性的独有生产特性，一旦发生事故，便会发生重大安全事故，造成的影响与损失无法估量，其灾难后果的长久性更是企业与国家所难以承受的。而我国的国情所致，中小型的危化企业占据了我国化工行业的半壁江山，且分布广泛，给国家的安全管理带来了巨大的困难和挑战[1]。因此，我国的中小型危化企业内部管理应加强对化工生产安全管理的重视，而化工企业安全管理控制中最重要的一环就是安全投入。这是决定企业安全生产水平高低的关键要素。而安全投入不足，恰恰是我国中小型危化工企业普遍存的问题，究其本质这也是我国危化行业事故发生率居高不下的主因之一。

1 中小型危化企业事故致因的安全投入

根据海因里希事故致因理论，我国中小型危化企业安全事故的事故致因可以从人、物、环境、管理4个方面来进行总结分析(详见表1)。

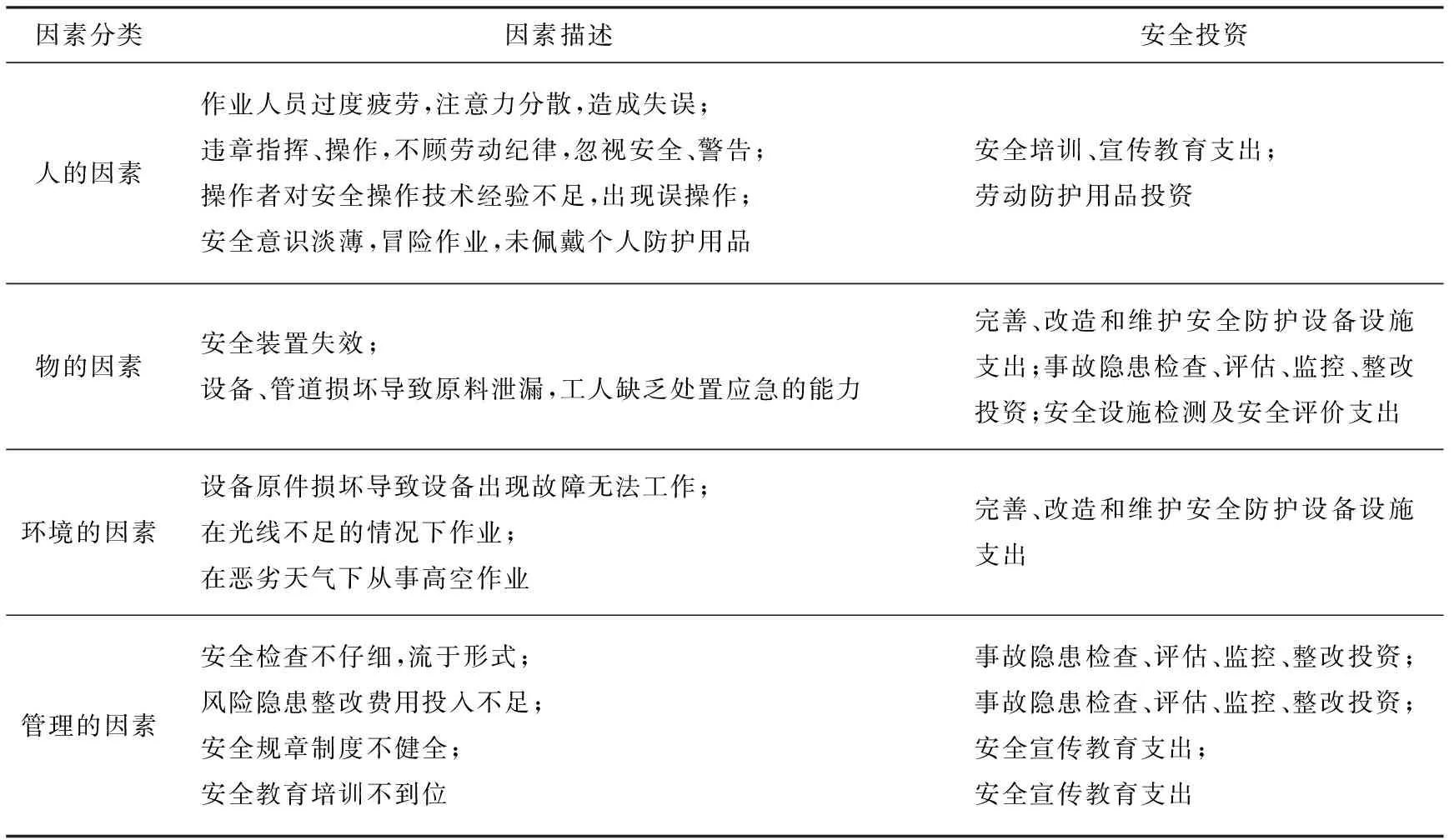
表1 事故致因整理和事故致因对应投入Table 1 Accident causation factors and corresponding investment

研究发现：通过合理、有针对性的加强安全投资，是可以消除相应的事故致因的。

2 中小型危险化工企业安全投入与效益分析

2.1 中小型危险化工企业安全投入分析

笔者根据《企业安全生产费用提取和使用管理办法》对化工生产企业安全投资的使用规定并通过调研中小型危化企业安全投资的实际情况,把中小型危化企业的安全投资分为6大类：①劳动防护用品投资；②安全评价、检测支出；③安全宣传教育投资；④完善、改造和维护安全防护设备、设施支出；⑤危险源、事故隐患检查、评估、监控、整改投资；⑥应急演练救援费。

2.2 化工企业安全效益分析

调研发现，目前我国中小型危化企业在进行安全投资过程中出现如下问题。①某些企业不愿意在安全生产方面投入过多的资金，认为会占用有限的生产投入资源；②有些企业领导对于安全特别重视，认为应该投入大量的资金来保障企业的安全生产且具有规划性；③还有些企业在进行安全投资时没有规划性，而是凭借着所谓的经验之谈，致使我国中小型化工企业安全事故频频发生，灾害后果让人触目惊心，给国家和人民造成巨大的损失。因此，如何利用有限的资源，处理企业安全与生产之间的关系这一矛盾共存体，如何精准地量化决策安全投资、实现最大安全经济效益，成为中小型危化企业掌舵人最为关心的问题。

笔者通过建立安全投入的减损产出模型和增值产出模型来量化中小型危化企业的安全经济效益，并确定最优的安全投入，企业决策时给予一定的指导。

3 化工企业安全产出分析

3.1 安全投入减损产出

安全经济损失不仅与安全投入大小有关，而且与安全投入结构有关[2]，用Cobb-Douglas生产函数形式建立安全投入与事故经济损失的函数关系，因此中小型危化企业安全投资优化前事故损失金额模型为：

(1)

中小型危化企业安全投资优化后，事故损失金额模型为：

(2)

中小型危化企业安全投资与事故损失的关系函数模型成立条件如下。

(1)f>0,故参数m>0。

(2) 系数αi<0(i=1，2，…，6)，说明只考虑改变某一类的安全投资而固定其余的安全投资，带来的影响就是事故损失的改变。

(3)由于ai<0,则极限lim(i=1,2,…,6),说明各安全分项投资的重要性都是极大的。

(4)设定企业劳动力这个投入要素为恒定。

(5)不考虑工艺技术改变的影响。

故中小型危化企业安全损失减少量为：

(3)

3.2 安全投入增值产出模型

企业产品总产值B与原料投资A0和对产品产量造成影响的事故有着紧密的关系[3]。根据企业产品总产值B与进行生产的投资和对产品产量造成影响的事故的函数关系可建立如下函数数学模型。

(1)中小型危化企业安全投资优化前产出模型

(4)

(2)中小型危化企业安全投资优化后产出模型

(5)

模型成立条件分析如下。

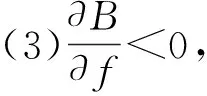
3.3 中小型危化企业安全经济效益优化模型

中小型危化企业安全经济效益优化模型

(6)

对于建立的模型(6)，运用偏导数求极值的数学方法及使用Matlab中有限制的非线性规划最大值命令fmincon求解，从而确定了企业各项最优的安全投资金额。

4 案例分析

以某企业为例，统计的历年投资及产值如表2所示。

根据该企业所统计的历年数据，确定各分项安全投资对该企业事故损失的影响程度以及计算，2018年计划生产投资为5 152.2万元时，企业决策安全投资能获得最大的安全经济效益。

利用SPSS软件对企业安全投入与事故经济损失进行多元线性回归，得到安全减损量为：

I1=f0-f=

63.355 77-1 302.305 83

拟合得出企业总产值与生产性投入和事故损失的模型，得出安全增值产出为：

得出安全经济效益模型化简为：

5 855.690 09-6 374.459 69k-0.974 9+

7 253.659 69e-19.123 38k-0.974 9-0.974 9k。

在Matlab软件里有求极值的命令功能，该模型求极值可是使用Matlab软件通过编写M源文件导入到优化工具箱中使用有限制的非线性规划最大值命令fmincon[4]，求出最优解k为199.57，即A1∶A2∶A3∶A4∶A5∶A6=23.786 95∶27.476 92∶11.794 76∶47.119 17∶66.295 99∶10.916 33。

因此，当该化工企业2018年度生产投资为5 152.2元时，按上述模型计算的最优分配比例，该年度企业安全效益最大值为416.089 7万元，最优的安全投资为187.390 12万元。

优化后的各项安全投入比例与原决策方案下各项安全投入比例对比如图1和图2所示。图1为原方案安全投资结构图，图2为优化后安全投资结构图。

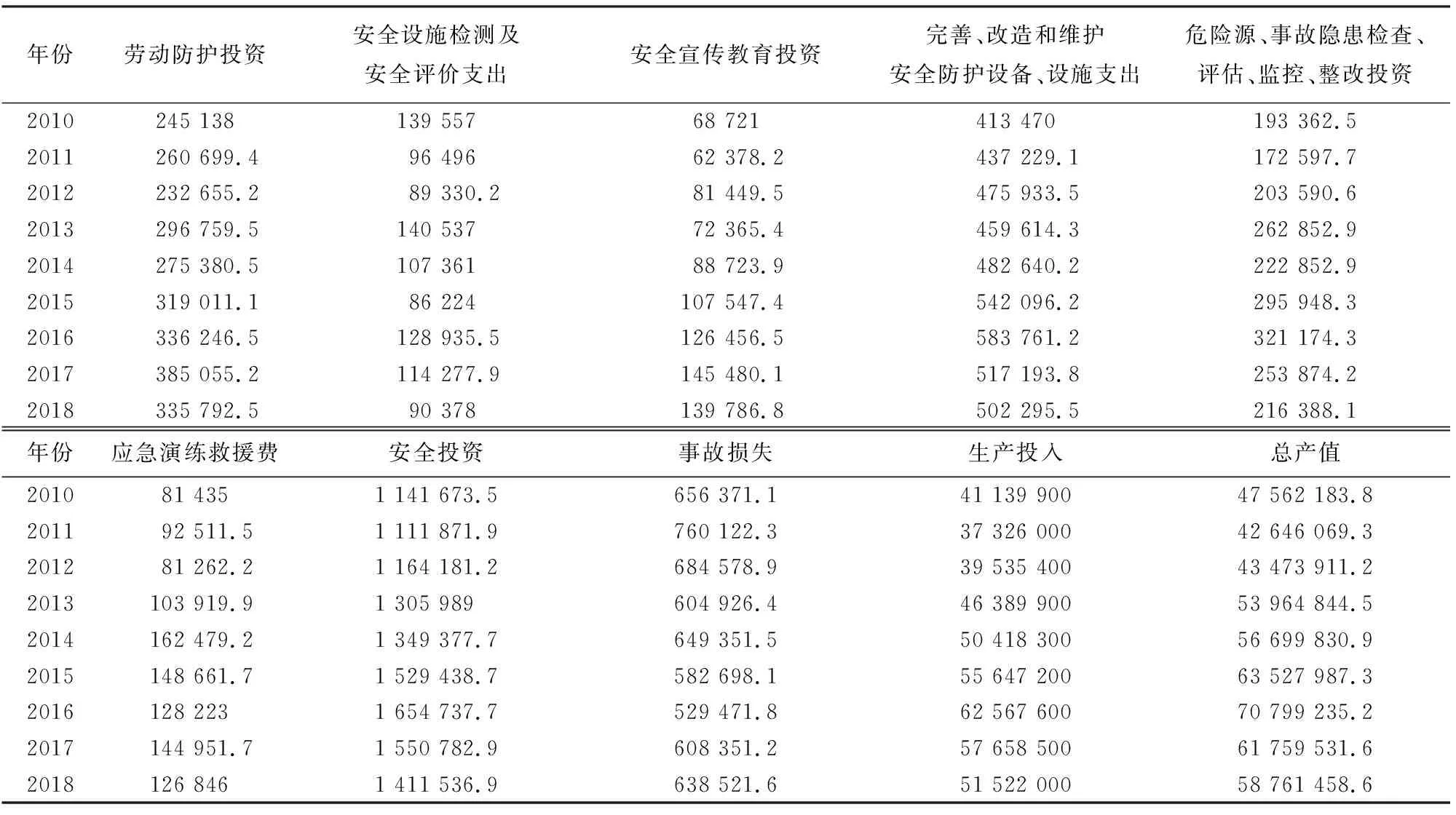
表2 企业历年投资及产值表Table 2 Enterprise investment and output value in recent years 元

注：2019年数据因其他原因未公开。

图1 原方案安全投资结构图Fig.1 Structure of safety investment of original scheme

图2 优化后安全投资结构图Fig.2 Optimized structure of safety investment

为判断中小型化工生产企业安全投资是否合理的方法，引用由美国Firth、Graham和Kinney依据“环境危险性LEC评价法”分析得出的安全投资的综合评分决策法[5]。根据该方法，该企业优化安全投资后，事故后果的严重性R依然为15分；员工们依旧要经常暴露于危险作业条件下，危险作业程度E为6分。

改变安全投资决策方向后事故只有意外或巧合才能发生，事故发生的可能性P的分值为3分；安全投资优化后金额为187.498 28万元，按照1人民币=0.147 1美元的汇率折算，则安全投入费用约为27.58万美元，经费指标C的分值为10。通过优化，有针对性的改善安全投资大大地降低了事故发生的可能性，减少了下次发生类似事故的概率，事故纠正程度得以提升，预计可以降低险情为50%～75%。因此纠正程度D的取分值为2分。将这些取值代入公式：

投入合理度=

得：投资合理度=

(15×6×3)÷(10×2)=13.5>10。

由此可以得出结论：优化后的安全投资资金是合理的。

5 结语

(1)运用SPSS、Matlab软件对该企业的安全经济效益最优模型求解,该企业于2018年度生产投资为5 152.2万元时,安全投资的最优比例为:23.79∶27.48∶11.79∶47.11∶66.29∶10.92。优化安全投资结构后可实现的安全效益最大值为416.089 7万元，最优的安全投资约187.39万元。

(2)该企业在2010年与2011年的安全投资是基本持平的，但是事故损失却呈现了较大的不同。对比图1，图2可知：该厂在2011年的安全投资结构中减小了危险源、事故隐患检查、评估、监控、整改投资的比例，正确解释了为什么2011年出现了比2010年更大的事故损失。

(3)2013—2014年，该厂虽然增加了安全总投资，但是事故损失仍旧增大。对比图1，图2的分析可知：是因为减小了危险源、事故隐患检查、评估、监控、整改投资以及安全设施检测及安全评价支出的比例。

(4)2016—2018年间，危险源、事故隐患检查、评估、监控、整改投资的比例是依次降低的，对比表2里2012年与2018年的各项数据，在改造和维护安全防护设备设施支出比例基本不变，劳动防护投资所占比例有所增加的情况下，企业的事故损失还是出现了大幅度的上升，这正是企业降低危险源、事故隐患检查、评估、监控、整改投资比例的效果。

(5)基于该企业的历年统计数据分析和模型优化结果分析，该企业在进行安全投入决策时，应将有限的安全投入资源优先投入到危险源、事故隐患检查、评估、监控、整改投资方面。